Logic, Explainability and Future of Understanding

Logic discovery

Logic is the basis of many things. But what is the basis of logic itself?

In character logic, characters like p and q are inserted, denoting statements (or “propositions”) of the type “this is an interesting essay”. There are also certain rules of logic, for example, for any p and any q the expression NOT (p AND q) is similar to (NOT p) OR (NOT q).

But where do these "rules of logic" come from? Logic is a formal system. Like Euclidean geometry, it can be constructed on axioms. But what are axioms? You can start with statements like p AND q = q AND p, or NOT NOT p = p. But how many axioms are required? How simple can they be?

This question has long been painful. But at 20:31 on Sunday, January 29, 2000, the only axiom appeared on my computer screen. I have already shown that nothing can be easier, but soon found that this single small axiom was enough to create all the logic:


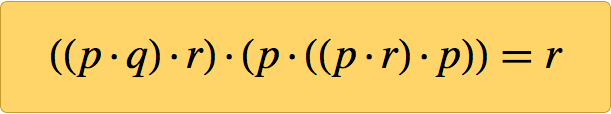
How was I to know that she was right? Because I made the computer prove it. And here is the proof that I printed in the book " New Type of Science " (already available in the Wolfram Data repository ):


Using the latest version of the Wolfram Language, anyone can generate this proof in less than a minute. And his every step is easy to check . But why the result will be correct? How to explain it?

Similar questions are increasingly being asked about all sorts of computing systems and applications related to machine learning and AI. Yes, we see what happens. But can we understand this?

I think that this question is deep in its essence - and crucial for the future of science and technology, and for the future of all intellectual development.

But before we talk about this, let's discuss the axiom that I discovered.

Story

Logic as a formal discipline comes from Aristotle, who lived in the 4th century BC. Within the framework of the work of his life on cataloging things (animals, causes, etc.), Aristotle compiled a catalog of admissible forms of arguments and created symbolic patterns for them, which, in fact, provided the main logic content for two thousand years to come.

However, by the 15th century algebra was invented, and with it a clearer idea of ​​things appeared. But it was not until 1847 that George Boole finally formulated logic in the same way as algebra, with logical operations of the type AND and OR, operating according to rules similar to the rules of algebra.

A few years later, people were already recording axiomatic systems for logic. A typical example was:


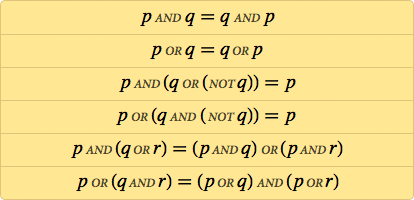
But do we really need AND, OR and NOT for the logic? After the first decade of the 20th century, several people have discovered that a single operation, which we now call NAND, will suffice, and, for example, p OR q can be calculated as (p NAND p) NAND (q NAND q). The “functional completeness” of NAND could have remained a wonder if not for the development of semiconductor technology — it implements all the billions of logical operations in a modern microprocessor using a combination of transistors that perform only the NAND function or the associated NOR.

Well, so how do the axioms of logic look in terms of NAND? Here is their first known version, written by Henry Schaeffer in 1913 (here the dot denotes NAND):


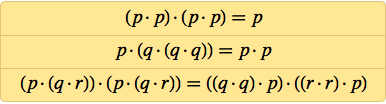
In 1910, Principia Mathematica, a three-volume work on the logic and philosophy of mathematics by Alfred North Whitehead and Bertrand Russell, popularized the idea that, perhaps, all mathematics can be derived from logic. Given this, it was quite interesting to study the question of how simple the axioms of logic can be. The most significant work in this area was carried out in Lviv and Warsaw (at that time these cities were part of Poland), in particular, Jan Lukasevich (as a side effect of his work in 1920 he invented a “Polish” notation that does not require brackets). In 1944, at the age of 66, Lukasevich fled from the advancing Soviet army and in 1947 ended up in Ireland.

Meanwhile, Irishman Carew Meredith, who studied at Winchester and Cambridge and became a mathematics teacher at Cambridge, was forced to return to Ireland in 1939 because of his pacifism. In 1947, Meredith got to Lukasevich’s lecture in Dublin, which inspired him to look for simple axioms, which he did, for the most part, the rest of his life.

Already by 1949, Meredith discovered a two-axiom system:


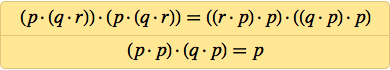
Almost 20 years later, in 1967, he managed to simplify it to:


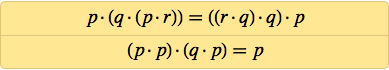
Is it possible to simplify this further? Meredith has been fiddling with this for years, figuring out where else extra NANDs can be removed. But after 1967, he no longer advanced further (and died in 1976), although in 1969 he found a three-axiomatic system:


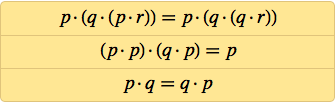
When I began to study the axiom systems of logic, I did not know anything about the work of Meredith. I was fascinated by this topic as part of trying to understand what kind of behavior can grow out of simple rules. In the 1980s, I made an unexpected discovery that even cellular automata with the simplest possible rules — such as my favorite rule 30 — can lead to incredibly complex behavior.

Having spent the 1990s trying to understand the commonality of this phenomenon, I finally wanted to see how it can be applied to mathematics. In mathematics, we, in fact, begin to work with axioms (for example, in arithmetic, in geometry, in logic), and then we try to prove a whole set of complex theorems based on them.

However, how simple can axioms be? That is what I wanted to establish in 1999. As a first example, I decided to study logic (or, equivalently, Boolean algebra). Refuting all my expectations, my experience with cellular automata, Turing machines and other systems - including even partial differential equations - says that you can simply start listing the simplest cases possible, and at some point see something interesting.

But is it possible to “open logic” in this way? There was only one way to say this. And at the end of 1999, I arranged everything to start exploring the space of all possible axiom systems, starting with the simplest.

In a sense, any axiom system defines a set of constraints, for example, on p · q. It does not say what p · q is, it only gives properties that p · q must satisfy (for example, it can state that q · p = p · q). Then the question is whether it is possible to deduce from these properties all the theorems of logic that are executed when p · q is Nand [p, q]: neither more nor less.

Something can be checked directly. We can take the axiom system and see which forms p · q satisfy the axioms, if p and q are, say, true and false. If the axiom system is that q · p = p · q, then yes, p · q can be Nand [p, q] - but not necessarily. It may also be And [p, q] or Equal [p, q], or many more other options that do not satisfy the same levels as the NAND function in logic. But by the time we reach the axiom system {((p · p) · q) · (q · p) = q}, we are reaching a state in which Nand [p, q] (and the equivalent Nor [p , q]) remain the only working models of p · q - at least, if we assume that q and p have only two possible values.

Is this then a system of axioms for logic? Not. Because it implies, for example, the existence of a variant, when p and q have three values, but there is no such thing in logic. However, the fact that this system of axioms from one axiom comes close to what we need indicates that it is worth looking for a single axiom from which logic is reproduced. This is exactly what I did in January 2000 (in our time, this task has become easier, thanks to the rather new and very convenient Wolfram Language, Groupings function).

It was quite easy to verify that axioms in which there were 3 or fewer NANDs (or "operator points") did not work. By 5 am on Sunday, January 29th (aha, then I was an owl), I found that the axioms containing 4 NANDs would not work either. When I stopped work, at about 6 am, I had 14 candidates in my arms with five NANDs. But having continued work on Sunday evening and having conducted additional tests, I had to drop them all.

Needless to say, the next step was to test the axioms with 6 NAND. They turned out to be 288 684. But my code worked efficiently, and not much time passed before the following appeared on the screen (yes, from Mathematica Version 4):


At first I did not understand what I did. I only knew that I had 25 nonequivalent axioms with 6 NANDs, which were able to advance further than axioms with 5 NANDs. But were there any axioms that gave rise to logic? I had an empirical method capable of discarding unnecessary axioms. But the only way to know exactly the correctness of a specific axiom was to prove that it is successfully able to reproduce, say, Schaeffer's axiom for logic.

It took a little play with the programs, but after a few days I found that most of the 25 axioms received did not work. As a result, two survived:



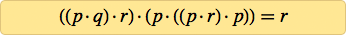
And to my great joy, I managed to prove with the help of a computer that both are axioms for logic. The technique used guaranteed the absence of simpler axioms for logic. Therefore, I knew that I had come to a goal: after a century (and maybe a couple of millennia) of searches, we can finally declare that we have found the simplest axiom for logic.

Soon after, I discovered systems of two axioms with 6 NANDs in general, which, as I proved, are capable of reproducing logic:



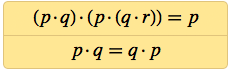
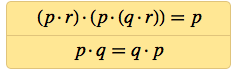
And if we take the commutativity p · q = q · p as a matter of course, then the logic can be obtained from an axiom containing only 4 NANDs.

Why is it important

Well, let's say, it is very cool to be able to say that someone “completed the work begun by Aristotle” (or at least by Boolem) and discovered the simplest possible system of axioms for logic. Is this just a curiosity, or does this fact have important consequences?

Before the platform developed by me in the book A New Kind of Science, I think it would be difficult to consider this fact to be more than just a wonder. But now it should be clear that he is connected with all sorts of basic questions, such as whether mathematics should be considered a discovery or an invention.

The kind of mathematics that people do is based on a handful of certain systems of axioms - each of which defines a particular area of ​​mathematics (logic, group theory, geometry, set theory). But speaking in the abstract, there is an infinite number of systems of axioms - each of which defines the area of ​​mathematics that can be studied, even if people have not done it yet.

Before the book A New Kind of Science, I apparently meant that everything that exists “somewhere there” in the computational universe should be “less interesting” than what people had created and studied. But my discoveries concerning simple programs indicate that in systems that are simply “somewhere out there” exist, no less rich possibilities are hidden than in systems carefully selected by people.

So what about the axiom system for mathematics? To compare the existing “somewhere out there” with what people have studied, you need to know whether the axiom systems for the existing areas of mathematics we have studied lie. And, based on traditional systems created by people, it can be concluded that they have to be somewhere very, very far away - and in general they can be found only if you already know where you are.

But my discovery of the axiom system answered the question “How far is the logic?” For such things as a cellular automaton, it is quite simple to number (as I did in the 1980s) all possible cellular automata. It is a little harder to do this with axiom systems - but not much. In one approach, my axiom can be designated as 411; 3; 7; 118 - or, in the Wolfram Language:


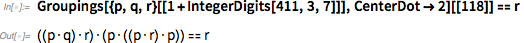
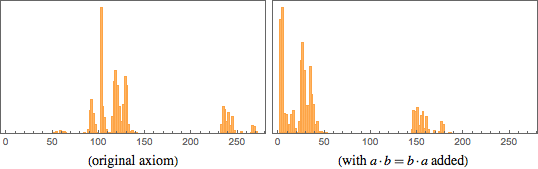
And, at least in the space of possible functional forms (not taking into account the marking of variables), there is a visual representation of the location of this axiom:


Given the fundamental importance of logic for such a large number of formal systems that people study, one could think that in any reasonable representation, logic corresponds to one of the simplest possible axioms. But at least in a presentation using NAND, this is not the case. For it, there is still a very simple system of axioms, but it is likely to prove to be a hundred-thousandth system of axioms from all possible that will occur if you simply start to number the systems of axioms, starting with the simplest.

Given this, the obvious next question will be: what about all the other systems of axioms? How do they behave? It is this question that explores the book A New Kind of Science. And in it, I argue that things like systems observed in nature are often better described by these very “other rules” that we can find, numbering possibilities.

As for systems of axioms, I made a picture representing what is happening in the "areas of mathematics" corresponding to various systems of axioms. The series shows the consequences of a certain system of axioms, and the squares denote the truth of a certain theorem in this system of axioms (yes, Gödel's theorem comes into force at some point, after which it becomes incredibly difficult to prove or disprove a given theorem in a given system of axioms; in practice, with my methods this happens just to the right of what is shown in the picture).


Is there something fundamentally special in the fields of mathematics that have been “studied by people”? Judging by this and other pictures, nothing obvious comes to mind. I suspect that there is only one peculiarity in these areas - the historical fact that they have been studied. (You can make statements like the fact that "they describe the real world" or "related to how the brain works," but the results described in the book state the opposite).

Well, well, what is the meaning of my axiom system for logic? Its size makes it possible to feel the final content of logic as an axiomatic system. And it makes us consider - at least for now - that we need to regard logic more as a “construction invented by man” than as a “discovery” that happened for “natural reasons”.

If history went differently, and we would constantly search (as it is done in the book) for a set of possible simplest systems of axioms, then we might have “discovered” a system of axioms for logic, like that system whose properties seem interesting to us. But since we have studied such a small number of all possible axiom systems, I think it would be reasonable to consider logic as an “invention” —a specially created construction.

In a sense, in the Middle Ages, logic looked like this — when possible syllogisms (permissible types of arguments) were represented as Latin mnemonics like bArbArA and cElErAnt. Therefore, it is now interesting to find the mnemonic representation of what we know now as the simplest axiom system for logic.

Starting with ((p · q) · r) · (p · ((p · r) · p)) = r, you can think of each p · q as a prefix or Polish record (inverse of the “reverse Polish record” of the HP calculator ) in the form of Dpq - therefore, the whole axiom can be written as = DDDpqrDpDDprpr. There is also an English mnemonic on this subject - FIGure OuT Queue, where the roles of p, q, r are played by u, r, e. Or you can look at the first letters of the words in the following sentence (where B is the operator, and p, q, r are a, p, c): “Bit by bit, a program computed Boolean algebra's best binary axiom covering all cases” [ gradually computed using the program, the best binary axiom of Boolean algebra describes all cases].

Proof mechanics

Okay, so how to prove the correctness of my axiom system? The first thing that comes to mind is to show that it is possible to derive from it a known system of axioms for logic - for example, the system of Schaeffer's axioms:


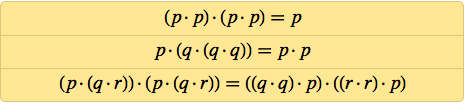
There are three axioms here, and we need to derive each. Here is what can be done to display the first, using the latest version of Wolfram Language:


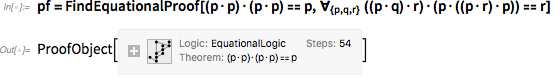
It is noteworthy that it has now become possible to do this. In the “object of the proof” it is written that 54 steps were used for the proof. Based on this object, we can generate a “notebook” describing each of the steps:


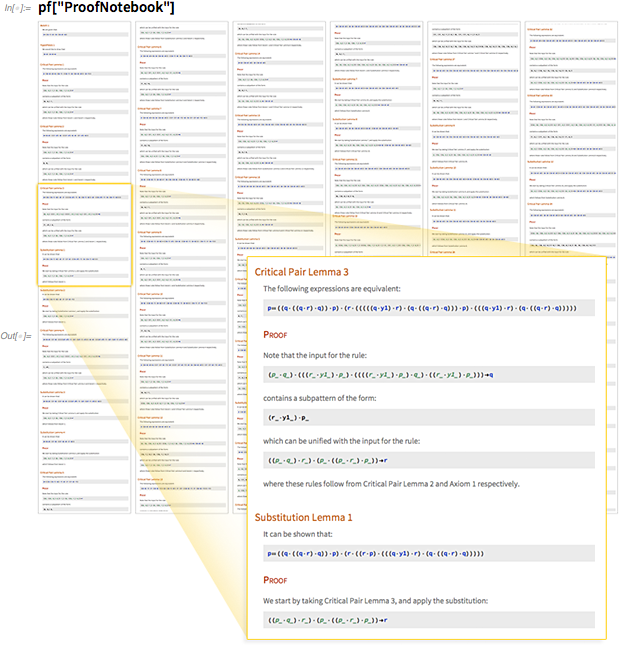
In general, the entire sequence of intermediate lemmas is proved here, which allows us to finally derive the final result. Between lemmas, there is a whole network of mutual dependencies:


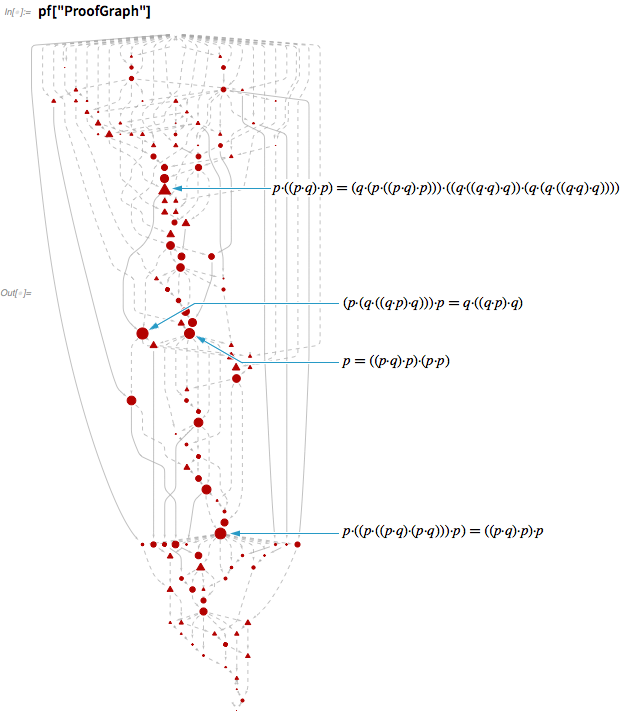
But the networks involved in the derivation of all three axioms in the system of Schaeffer's axioms - for the latter, an incredible 504 steps are used:


Yes, it is obvious that these networks are rather confused. But before discussing what this complexity means, let's talk about what happens at each step of this evidence.

The main idea is simple. Imagine that we have an axiom, which is simply written as p · q = q · p (mathematically, this means that the operator is commutative). More precisely, the axiom says that for any expressions p and q, p · q is equivalent to q · p.

Well, suppose we want to deduce from this axiom that (a · b) · (c · d) = (d · c) · (b · a). This can be done using the axiom to transform d · c into c · d, b · a into a · b, and finally, (c · d) · (a · b) into (a · b) · (c · d ).

FindEquationalProof does essentially the same thing, although it does not follow these steps in exactly the same order, and changes both the left side of the equation and the right side.


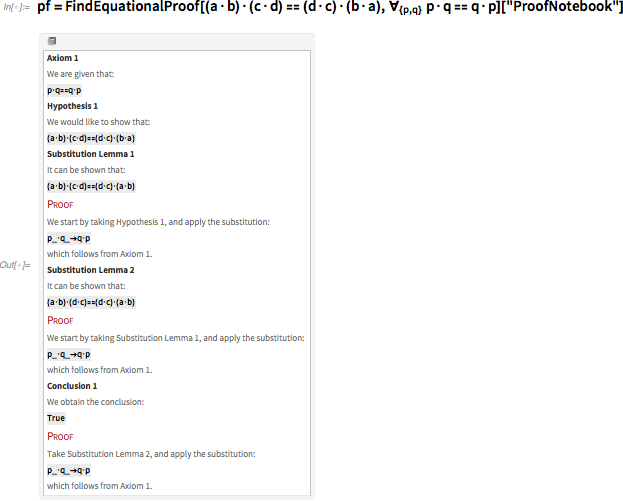
Having obtained such evidence, you can simply track each step and verify that they give the stated result. But how to find evidence? There are many possible sequences of substitutions and transformations. How to find a sequence that successfully leads to the final result?

It would be possible to decide: why not try all possible sequences, and if there is a working one among them, should it end up? The problem is that you can quickly come to an astronomical number of sequences. The main part of the art of automatic proof of theorems consists of finding ways to reduce the number of sequences to check.

It quickly slips into technical details, but the basic idea is easy to discuss if you know the basics of algebra. Suppose we are trying to prove an algebraic result like


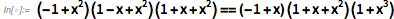
There is a guaranteed way to do this: simply by applying the rules of algebra to reveal each of the parties, you can immediately see their similarities:


Why does this work? Because there is a way to work with such expressions, systematically reducing them until they take the standard form. Is it possible to do the same operation in arbitrary axiom systems?

Not right away. In algebra, this works because it has a special property that ensures that you can always “move forward” along the path to simplify expressions. But in the 1970s, various scientists discovered independently several times (under names like the Knut-Bendix algorithm or Gröbner basis ) that even if the axiom system does not have the necessary intrinsic properties, it is potentially possible to find "additions" to this system in which there is.

This is what happens in the typical evidence that FindEquationalProof produces (based on the Waldmeister system, “master of trees”). There are so-called. “Lemmas of Critical Pairs” that do not directly advance proof, but make possible the emergence of paths capable of this. Complicated by the fact that, although the final expression we want to get is rather short, on the way to it, you may have to go through a much longer intermediate expression. Therefore, for example, the proof of the first Schaeffer axiom has such intermediate steps:


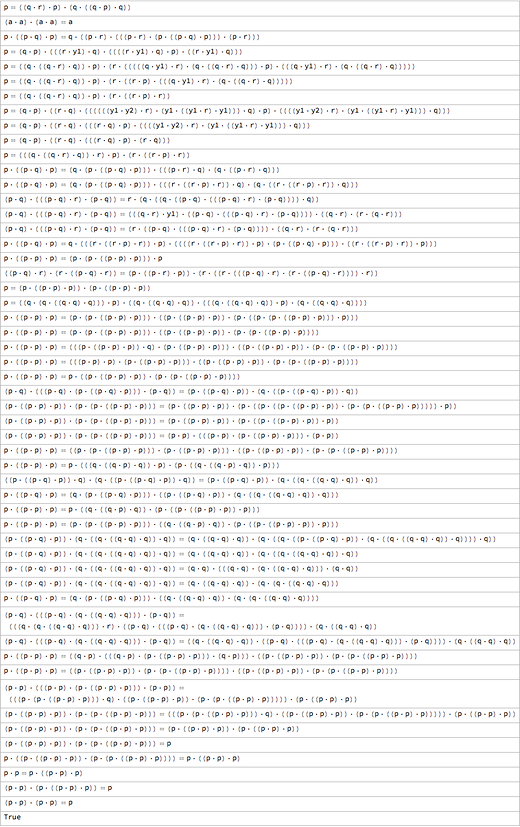
In this case, the largest of the steps is 4 times more than the original axiom:


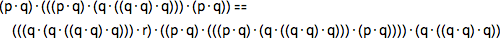
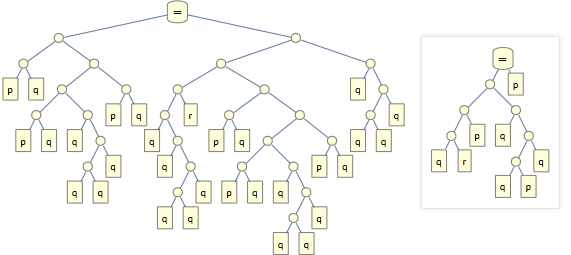
Such expressions can be represented as a tree. Here is its tree, in comparison with the tree of the original axiom:


And here is how the sizes of intermediate steps develop in the course of the proofs of each of Schaeffer's axiom:

Why is it so hard?

Is it surprising that this evidence is so complex? Not really. After all, we are well aware that mathematics can be difficult. In principle, it could be that all the truths in mathematics would be easy to prove. But one of the side effects of the 1931 Gödel theorem is that even for those things that have evidence, the path to them can be arbitrarily long.

This is a symptom of a much more general phenomenon, which I call computational irreducibility . Consider a system governed by a simple cellular automaton rule (of course, in any of my essays somewhere there will necessarily be cellular automata). Run this system.


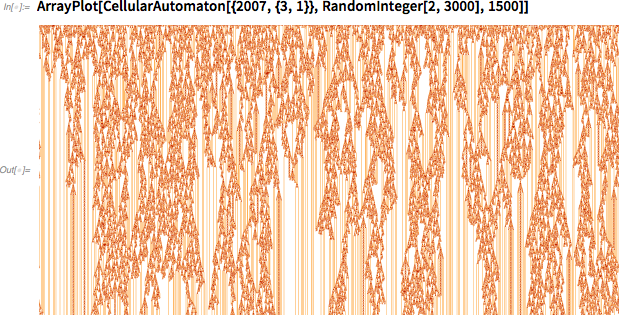
One could decide that if the system is based on a simple rule, then there should be a quick way to understand what the system is doing. But it is not. According to my principle of computational equivalence , the work of the system often corresponds to calculations, the complexity of which coincides with any calculations that we could carry out in order to understand the behavior of the system. This means that the actual behavior of the system, in fact, corresponds to an amount of computational work that cannot be reduced in principle.

Regarding the picture above: let's say we want to know if the pattern will die as a result. We could continue to carry it out, and if we are lucky, it will eventually degenerate into something, the fate of which will be obvious. However, in general, there is no upper limit on how much time we have to spend, in fact, on evidence.

When something like this happens with logical evidence, it happens a little differently. Instead of running something that works according to certain rules, we ask if there is a way to reach a certain result, after going through several steps, each of which obeys a certain rule. And this task, as a practical computational problem, turns out to be much more difficult. But the essence of complexity is the same phenomenon of computational irreducibility, and this phenomenon suggests that there is no general way of briefly circumventing the process of studying what the system will do.

Needless to say, there are many things in the world - especially in technology and scientific modeling, as well as in areas where various forms of rules are present - traditionally designed to avoid computational irreducibility, and work so that the result of their work is immediately visible. without the need to carry out unreducible number of calculations.

But one of the consequences of my computational equivalence principle is that these cases are single and unnatural - he argues that computational irreducibility exists in all systems of the computational universe.

What about mathematics? Maybe the rules of mathematics are specially chosen to demonstrate computational reducibility. And in some cases this is the case (and in some sense it also happens in logic). But for the most part, it seems that the axiom systems of mathematics are not atypical for the space of all possible axiom systems - where computational irreducibility inevitably rages.

Why do we need evidence?

In a sense, proof is needed to know the truth of something. Of course, especially in our time, the proof faded into the background, giving way to pure computation. In practice, the desire to generate something by calculations is much more common than the desire to “step back” and construct a proof of the truth of something.

In pure mathematics, however, one often encounters concepts that include, at least nominally, an infinite number of cases (“true for all primes,” etc.), for which head-on calculations are not suitable. . And when the question of confirmation arises (“can this program end with an error?” Or “can this cryptocurrency be spent twice?”) It is more reasonable to try to prove this than to calculate all possible cases.

But in real mathematical practice, proof is more than finding out the truth. When Euclid wrote his " Beginnings ", he simply indicated the results, and the evidence "left to the reader." But, one way or another, especially in the last century, evidence has turned into something that does not just happen behind the scenes, but is the main carrier through which it is necessary to translate concepts.

It seems to me that as a result of some fad history, evidence is being offered today as a subject that people have to understand, and programs are considered just something that a computer has to do. Why did it happen so? Well, at least in the past, the evidence could be presented in text form - therefore, if anyone used them, then only people. A program is almost always recorded in the form of a computer language. And for a very long time these languages ​​were created so that they could be more or less directly translated into low-level computer operations — that is, the computer understood them right away, but people did not necessarily.

But one of the main goals of my activity over the past few decades was to change this state of affairs, and to develop in Wolfram Language a real “language of computational communication” in which computational ideas can be transmitted so that both computers and people can understand them.

Such a language has many consequences. One of them is the changing role of evidence. Suppose we are looking at some mathematical result. In the past, the only plausible way to bring it to the point of understanding was to produce evidence readable by people. But now another is possible: you can issue a program for the Wolfram Language, which counts the result. And this is in many ways a much richer way to convey the truth of the result. Each part of the program is something precise and unambiguous - anyone can start it. There is no such problem as trying to understand some part of the text that requires filling in certain spaces. Everything is stated in the text quite clearly.

What about evidence? Are there clear and precise ways to write evidence? Potentially yes, although it is not particularly easy. And although the foundation of the Wolfram Language has existed for 30 years, only today there has emerged a reasonable way to present with its help such structurally straightforward proofs as one of my axioms above.

You can imagine the creation of evidence in Wolfram Language just as people create programs — and we are working to provide high-level versions of such “help with evidence” functionality. However, nobody created the proof of my axiom system - the computer found it. And this is more like the output of the program than the program itself. However, like the program, the proof in some sense can also be “run” to verify the result.

Creating clarity

Most of the time, people using Wolfram Language, or Wolfram | Alpha, want to calculate something. They need to get a result, and not understand why they got exactly such results. But in Wolfram | Alpha, especially in such areas as mathematics and chemistry, a popular feature among students is the construction of “step-by-step” solutions.


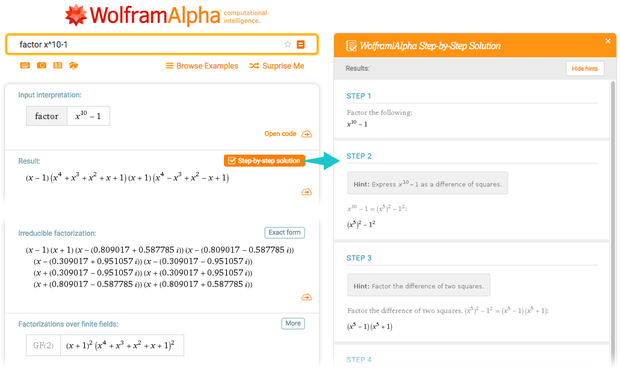
When the Wolfram | Alpha system calculates, for example, the integral, it uses all sorts of powerful algorithmic techniques that are optimized for getting answers. But when she is asked to show the stages of calculations, she does something else: she needs to explain step by step why exactly this result is obtained.

There would be no use in explaining how the result was actually obtained; This is a very inappropriate process for humans. She needs to understand which operations people have learned can be used to get results. Often she comes up with some useful trick. Yes, she has a systematic way for this that always works. But there are too many “mechanical” stages in it. A "trick" (substitution, partial integration, etc.) does not work in the general case, but in this particular case it will give a faster way to the answer.

And what about getting clear versions of other things? For example, work programs in the general case. Or evidence of my axiom system.

Let's start with the programs. Suppose we wrote a program and want to explain how it works. One of the traditional approaches is to include comments in the code. If we write in a traditional low-level language, this may be the best way. But the whole point of the Wolfram Language as a language for computational communication is that the language itself should allow the transmission of ideas without the need to include additional pieces of text.

It is necessary to expend efforts so that the program on the Wolfram Language is a good description of the process, as well as that the simple text in English is a good description of the process. However, you can get such a piece of code on Wolfram Language, which very clearly explains how everything works, by itself.

Of course, it often happens that the actual execution of the code leads to such things that are not obvious from the program. I will soon mention such extreme cases as cellular automata. But for now, let's imagine that we have created a program that allows us to imagine what it does in general.

In this case, I found that computational essays presented in the form of Wolfram Notebooks are an excellent tool for explaining what is happening. It is important that the Wolfram Language, it allows you to run even the smallest parts of the programs separately (with the corresponding symbolic expressions in the role of input and output data). After that, you can imagine the sequence of program steps as a sequence of elements of a dialogue that forms the basis of a computational notebook.

In practice, it is often necessary to create visualizations of input and output data. Yes, everything can be expressed in the form of a single symbolic representation. But it is much easier for people to understand the visual representation of things than any one-dimensional language-like line.

Of course, creating good visualizations is akin to art. But at Wolfram Language we did a great job of automating this art - often with the help of quite complex machine learning and other algorithms that perform such things as the layout of networks or graphic elements.

What about starting with a simple program tracking? It is hard to do. I have experimented with this for decades, and have never been completely satisfied with the results. Yes, you can zoom in and see many details of what is happening. But I didn’t find enough good technicians to understand the whole picture, and automatically give out some particularly useful things.

At some level, this task is similar to reverse engineering. You are shown the machine code, chip circuit, whatever. And you need to take a step back and recreate a high-level description that repelled a person who somehow “compiled” into what you see.

In the traditional approach to engineering, when people create a product in steps, always having the ability to foresee the consequences of what they create, this approach can in principle work. But if instead you just wander around the computational universe in search of an optimal program (the way I looked for possible axiom systems to find a system for logic), then there is no guarantee that there will be some kind of “human history” or explanation behind this program.

A similar problem occurs in the natural sciences. You see how a complex set of all processes develops in a biological system. Is it possible to subject them to "reverse engineering" in order to find an "explanation"? Sometimes it can be said that evolution with natural selection will lead to this. Or that it is often found in the computational universe, so the probability of its occurrence is high. But there is no guarantee that the natural world is necessarily designed so that people can explain it.

Naturally, in modeling things, we inevitably consider only aspects that interest us, and we idealize everything else. And especially in areas such as medicine, one often has to work with an approximate model with a shallow decision tree that is easy to explain.

Nature of explanability

What does the phrase “something can be explained” mean? In essence, this means that people can understand this.

What is required of people in order to understand something? We need to somehow realize this. Take a typical cellular automaton with complex behavior. The computer has no problems to go through every step in its evolution. With great effort and effort, man could reproduce the work of the computer.

But one cannot say that in this case the person would “understand” what the cellular automaton is doing. For this, a person would have to easily talk about the behavior of the cellular automaton at a high level. Or, in other words, a person would have to be able to “tell a story” about the behavior of an automaton that other people could understand.

Is there a universal way to do this? No, due to computational irreducibility. However, it may happen that certain features that are important to people can be explained at a high level with certain limitations.

How it works? To do this, you need to create a certain high-level language that can describe the features of interest to us. Studying a typical drawing of a cellular automaton, one can try to speak not in terms of the colors of a huge number of individual cells, but in terms of higher level structures that can be detected. The main thing is that you can compile at least a partial catalog of such structures: although they will have many details that do not fit into the classification, certain structures are often found.

And if we want to start “explaining” the behavior of the cellular automaton, we will begin with the name of the structures, and then we will tell about what happens from the point of view of these structures.


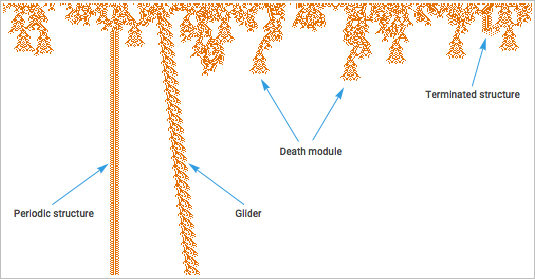
The cellular automaton case has one simplifying feature: because it works on the basis of simple deterministic rules, it has equally repeating structures. In nature, for example, we usually do not encounter such identical repetition. There's just one, say, a tiger, very similar to the other, so we call them both "tiger", although the arrangement of their atoms is not identical.

What is the general meaning of all this? It consists in using the idea of ​​symbolic representation. We say that we can assign a certain symbol - often this word - which can be used to symbolically describe a whole class of things, without listing in detail all the components of these things every time.

This is similar to information compression: we use symbolic constructions to find a more concise way of describing things that interest us.

Suppose we have generated a giant structure, for example, a mathematical one:


The first step is to create some kind of high-level internal representation. For example, we can find reusable structures. And we can give them names. And then show the "skeleton" of the whole structure with their help:


Yes, this scheme, similar to the “dictionary compression” scheme, is useful for reaching the first level of explanability.

But let's go back to the proof of my axiom system. The lemmas created in this proof are specially chosen as reusable elements. However, by excluding them, we are still left with evidence that people cannot understand right away.

What other step can you take? We need to come up with some description of a higher level. What could it be?

Concept concepts

If you are trying to explain something to someone, then it will be much easier to do if you find something else, but similar, that the person has already been able to understand. Imagine how you will explain the concept of the modern drone to a person from the Stone Age. It will be difficult to do. But it will be much easier to explain this to a man who lived 50 years ago, and who has already seen helicopters and model airplanes.

And in the end, the bottom line is that when we explain something, we do it in a language known to us as well as to the one to whom we explain it. And the richer the language, the less new elements we have to introduce in order to convey what we are trying to explain.

There is a pattern that repeats throughout the history of the mind. A certain set of things notice many times. Gradually, they begin to understand that these things are somehow abstractly similar, and all of them can be described in terms of a new concept, which is described by some new word or phrase.

Let's say we noticed things like water, blood, and oil. At some point, we understand that there is a generalized concept of "fluid", and all of them can be described as liquid. And when we have such a concept, we can begin to argue in its terms, finding more concepts — say, viscosity — based on it.

When does it make sense to combine things into a concept? A difficult question that cannot be answered without having foreseen all that can be done with this concept. In practice, in the process of evolution of the language and ideas of man, a certain process of consistent approximation is observed.

In the modern system of machine learning occurs much like a faster summation of information. Imagine that we took all sorts of objects around the world, and fed them FeatureSpacePlot functions to see what happens. If we get certain clusters in the space of singularities, then we can conclude that each of them can be defined as corresponding to some kind of “concept”, which can be, for example, marked with a word.

Honestly, what happens with FeatureSpacePlot - as in the process of human intellectual development - is in a sense a step-by-step process. To distribute features across feature spaces, FeatureSpacePlot uses features that it learned to extract based on previous categorization attempts.

Well, if we accept the world, what it is, what best categories — or concepts — can we use to describe things? This issue is constantly evolving. And in general, all breakthroughs - be it science, technology or something else - are often accurately associated with an awareness of the ability to usefully identify a new category or concept.

But in the process of evolution of our civilization there is a certain spiral. First, some definite concept is defined - for example, the idea of ​​a program. After that, people begin to use it and reflect on it in terms. Pretty soon, on the basis of this concept, many different concepts are constructed. And then another level of abstraction is defined, new concepts are created, based on the previous one.

History is characteristic of the technological set of knowledge of modern civilization, and its intellectual set of knowledge. Both there and there are towers of concepts and levels of abstraction one after another.

Learning problem

So that people can communicate using a certain concept, they need to learn about it. And, yes, some concepts (such as the constancy of objects) are automatically realized by people, just by observing nature. But, let's say, if you look at the list of common words of modern English, it becomes clear that most of the concepts used by our modern civilization do not apply to those that people are aware of independently, observing nature.

Instead, which is very much like modern machine learning, they need a special knowledge of the world "under supervision", organized in order to emphasize the importance of certain concepts. And in more abstract areas (such as mathematics), they probably need to face concepts in their immediate abstract form.

Well, will we need to find out more and more all the time as the amount of accumulated intellectual knowledge of civilization increases? There may be anxiety that at some point our brain simply will not be able to keep up with the development, and we will have to add some extra help. But it seems to me that this is, fortunately, one of those cases where the problem can be solved "at the software level."

The problem is this: at any time in history there is a certain set of concepts that are important for life in the world during this period. And, yes, with the development of civilization, new concepts are revealed and new concepts are introduced. However, there is another process: new concepts introduce new levels of abstraction, usually including a large number of earlier concepts.

We can often observe this in technology. There was a time when working on a computer needed to know a lot of low-level details. But over time, these details are abstracted, so now you need only a general concept. You click on the icon and the process starts - you do not need to understand the subtleties of operating systems, interrupt handlers, schedulers, and all other details.

And, of course, the Wolfram Language provides an excellent example of such work. It makes a lot of effort to automate a lot of low-level details (for example, which of the algorithms should be used) and allows users to think with high-level concepts.

Yes, people are still needed who understand the details that underlie the abstractions (although I’m not sure how many stone mites modern society needs). But for the most part, education can concentrate on a high level of knowledge.

It is often assumed that in order to achieve high-level concepts in the process of teaching a person, you first need to somehow summarize the history of how they came to these concepts historically. But usually - and, perhaps, always - it seems to be wrong. We can give an extreme example: imagine that in order to learn how to work with a computer, you first need to go through the entire history of mathematical logic. However, in reality, it is known that people immediately turn to modern concepts of computing, without having to learn any history.

But how does the network's conceptual clarity look like? Are there concepts that can be understood only by understanding other concepts? Given the training of people on the basis of interaction with the environment (or the training of a neural network), it is likely that there may be some order of them.

But it seems to me that a certain principle, similar to the universality of calculations, suggests that having a “clean brain” in your hands, you can start from anywhere. So, if some newcomers would learn about category theory and almost nothing else, they would no doubt have built a network of concepts where this theory is at its root, and what we know as the basics of arithmetic would be studied somewhere in the analogue of our institute.

Of course, such aliens could build their own set of technologies and their environment in a very different way from us - just like our history could have become completely different if computers could be successfully developed in the 19th century, and not in the middle of the 20th.

Math progress

I often thought about the extent to which the historical trajectory of mathematics is subject to the role of chance, and to what degree it was inevitable. As I already mentioned, at the level of formal systems there are many possible systems of axioms on which something can be constructed that is formally reminiscent of mathematics.

But the real history of mathematics did not begin with an arbitrary system of axioms. At the time of the Babylonians, it began with attempts to use arithmetic for commerce and for geometry with the goal of developing the land. And from these practical roots began to add further levels of abstraction, which eventually led to modern mathematics - for example, the numbers gradually generalized from positive integers to rational, then to roots, then to all integers, to decimal fractions, to complex numbers, to algebraic numbers, to quaternions , and so on.

Is there an inevitability of such a development of abstractions? I suspect that to some extent, yes. Perhaps the same is true of other types of concept formation. Having reached a certain level, you get the opportunity to study various things, and over time, the groups of these things become examples of more general and abstract constructions - which in turn define a new level, starting from which you can learn something new.

Are there ways to break out of this cycle? One of the possibilities may be related to mathematical experiments. You can systematically prove things related to certain mathematical systems. But you can empirically just notice mathematical facts — like Ramanujan noticed once that $$very close to the whole number. The question is: are such things "random mathematical facts" or are they somehow embedded in the "fabric of mathematics"?

The same question can be asked about the questions of mathematics. Is the question of the existence of odd perfect numbers (the answer to which has not been found since the days of Pythagoras) the key question for mathematics, or is it in some sense a random question not related to the fabric of mathematics?

In the same way as it is possible to number systems of axioms, it is possible to present numbering of possible questions in mathematics. But this immediately causes a problem. Godel's theorem asserts that in such axiom systems as the one that relates to arithmetic, there are “formally insoluble” theorems that cannot be proved or disproved within the framework of this axiom system.

However, the specific examples created by Gödel seemed very far from what could really arise in the course of studying mathematics. And for a long time it was believed that in some way the phenomenon of insolvability was something that, in principle, exists, but it will not have a relation to “real mathematics”.

However, according to my principle of computational equivalence and my experience in the computational universe, I am almost sure that this is not the case - and that, in fact, undecidability is very close even in typical mathematics. I would not be surprised if the tangible part of the unsolved problems of mathematics today (the Riemann hypothesis , P = NP, etc.) prove to be insoluble.

But if around is completely undecidable, how is it that so much of everything in mathematics is successfully resolved? I think this is because successfully solved problems were specially chosen to avoid insolvability, simply because of how the development of mathematics is structured. Because if we, in fact, form consistent levels of abstraction, based on the concepts that we have proved, then we pave the way able to move forward without turning into undecidability.

Of course, experimental mathematics or “random questions” can immediately lead us to a field full of undecidability. But, at least for now, the basic discipline of mathematics has evolved wrong.

And what about these "random facts of mathematics"? Yes, the same as with other areas of intellectual research. “Random facts” are not included in the path of intellectual development until a structure — usually some abstract concepts — is built around them.

A good example is my favorite discoveries of the origin of complexity in such systems, usually 30 cellular automata. Yes, similar phenomena have already been observed even thousands of years ago (for example, randomness in a sequence of prime numbers). But without a broader conceptual platform, few people paid attention to them.

Another example is nested sequences (fractals). There are some examples of how they met in the mosaic of the XIII century, but no one paid attention to them until the whole platform appeared around the fractals in the 1980s.

The same story repeats over and over: until abstract concepts are defined, it is difficult to talk about new concepts, even when faced with the phenomenon that demonstrates them.

I suspect that it is the same in mathematics: there is a certain inevitable overlap of some abstract concepts on top of others, defining the trajectory of mathematics. Is this path unique? No doubt not. In the vast space of possible mathematical facts, there are certain directions that are chosen for further constructions. But you could choose others.

Does this mean that themes in mathematics are inevitably given by historical accidents? Not as much as one might think. Indeed, as mathematics has been discovered again and again, starting with such things as algebra and geometry, there is a remarkable tendency in which different directions and different approaches lead to equivalent or corresponding to each other results.

Perhaps, to some extent, this is a consequence of the principle of computational equivalence, and the phenomena of computational universality: although the basic rules (or “language”) used in different areas of mathematics are different, the translation method between them appears as a result - and at the next level of abstraction The path chosen will no longer be so critical.

Logical proof and automation of abstraction

Let's return to logical proofs. How are they related to typical math? So far, nothing. Yes, the proof has nominally the same form as the standard mathematical proof. But it is not "friendly to people-mathematicians." These are only mechanical parts. It is not related to high-level abstract concepts that will be understood by the person-math.

It would help us a lot if we found out that non-trivial proof lemmas already appeared in the mathematical literature (I don’t think it was so, but our ability to search by theorems has not yet reached such a level that we can be sure). But if they do, it will probably give us a way to relate these lemmas to other things in mathematics, and define their circle of abstract concepts.

But how to make the proof explicable without it?

Perhaps there is some other way to carry out the proof, which is fundamentally stronger connected with the existing mathematics. But even with the evidence that we have now, one can imagine the “tweaking” of new concepts that would define a higher level of abstraction and place this evidence in a more general context.

Not sure how to do this. I was considering the possibility of nominating an award (something like my 2007 award for the Turing machine) for the “transformation of evidence into explicable form”. However, it is completely incomprehensible how to assess the “explanability”. One would be asked to record an hour-long video in which a successful explanation of the proof suitable for a typical mathematician would be given - but this would be very subjective.

But just as it is possible to automate the search for beautiful network layouts, it is possible that we can also automate the process of turning evidence into explicable. The current proof, in fact, without explanation, suggests to consider several hundred lemmas. But suppose we could define a small number of “interesting” lemmas. Perhaps we could somehow add them to our canon of famous mathematics, and then we would be able to use them to understand the proof.

There is an analogy with the development of languages. Creating the Wolfram Language, I try to identify the “pieces of computational work” that people often need. We create from them functions built into the language, with specific names that people can use to refer to them.

A similar process is going on - although not at all in such an organized way - in the evolution of natural languages. “Pieces of meaning”, which prove to be useful, end up with their words in the language. Sometimes they begin with phrases consisting of several existing words. But the most influential usually find themselves so far from existing words that they appear in the form of new words, which are potentially quite difficult to define.

When developing the Wolfram Language, the functions of which are called using English words, I rely on the general human understanding of the English language (and sometimes on the word comprehension used in common computer applications).

It would be necessary to do something similar in determining which lemmas to add to the mathematical canon. It would be necessary not only to make sure that each lemma would somehow be “interesting in essence”, but also if possible to choose lemmas that are “easy to deduce” from the existing mathematical concepts and results.

But what makes the lemma "interesting in its essence"? I must say that before I worked on my book, I accused of choosing lemmas (or cups) in any area of ​​mathematics that is described and named in textbooks, a great deal of arbitrariness and historical accidents.

But, having analyzed the theorems from the base logic in detail, I was surprised to find something completely different. Suppose that we have built all the correct theorems of logic in the order of their size
(for example, p = p will be the first, p AND p = p - a little later, etc.). This list has quite a lot of redundancy. Most theorems turn out to be a trivial extension of theorems that have already appeared in the list.

But sometimes a theorem appears, producing new information that cannot be proved on the basis of theorems that have already appeared in the list. A remarkable fact: there are 14 such theorems , and they, in fact, correspond exactly to the theorems that are usually given names in logic textbooks (here AND is ∧, OR is ∨, and NOT is ¬.)


In other words, in this case the named, or “interesting” theorems are precisely those that make statements about the new information of the minimum size. Yes, by such a definition, after some time, there is no longer any information left, since we will get all the axioms necessary to prove everything that can be done - although you can go further by starting to limit the complexity of admissible evidence.

What about the NAND theorems, for example, those found in the proof? Again, one can construct all true theorems in order, and find which ones cannot be proved on the basis of the previous theorems from the list:


NAND does not have a historical tradition like AND, OR and NOT. And, apparently, there is no human language in which NAND would be denoted by one word. But in the list of theorems of NAND, the first of the noted ones is easily recognized as the commutativity of NAND. After that, only a few translations are needed to give them names: a = (a · a) · (a · a) is like a double negative, a = (a · a) · (a · b) is like an absorption law , (a · A) · b = (a · b) · b is similar to “easing”, and so on.

Well, if we are going to learn a few "key theorems" of NAND logic, what kind of theorems should these be? Perhaps this should be the “popular lemmas” in the proofs.

Of course, any theorem can have many possible proofs. But, let's say, we will use only the evidence that FindEquationalProof produces. Then it turns out that in the proof of the first thousand NAND theorems the most popular lemma is a · a = a · ((a · a) · a), followed by lemmas of the type (a · ((a · a) · a)) · ( a · (a · ((a · a) · a))) = a.

What are these lemmas? They are useful for the methods used by FindEquationalProof. But for people, they seem to be not very suitable.

What about lemmas that turn out to be short? a · b = b · a is definitely not the most popular, but the shortest. (a · a) · (a · a) = a is more popular, but longer. There are also such lemmas as (a · a) · (b · a) = a.

How useful will these lemmas be? Here is one way to test this. Let's look at the first thousand NAND theorems and estimate how much the addition of lemmas shortens the proofs of these theorems (at least those found by the FindEquationalProof):


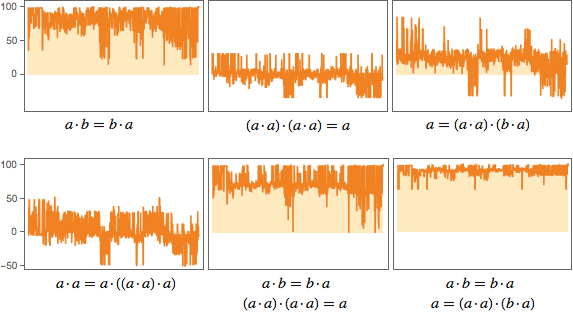
a · b = b · a is very successful, and often cuts evidence by almost 100 steps. (a · a) · (a · a) = a is much less successful; it sometimes even “confuses” FindEquationalProof, forcing it to take more steps than necessary (negative values ​​on the graphs). (a · a) · (b · a) = a does a good job with a contraction, but not as good as a · b = b · a. Although, if you combine it with a · b = b · a, as a result, contractions happen more often.

The analysis can be continued, for example, by including a comparison of how much a particular lemma shortens the lengths of evidence with respect to their original length. But the problem is that if you add a few “useful lemmas” like a · b = b · a and (a · a) · (b · a) = a, there are still many long proofs - that is, a lot of what is needed "understand".

What can we understand?

There are different ways of modeling things. For several hundred years, the exact science dominated the idea of ​​finding mathematical equations that could be solved to show how the system behaves. But since the appearance of my book, there has been an active shift in creating programs that can be run to see how the systems behave.

Sometimes such programs are written for a specific task; sometimes they are long sought. And nowadays, at least one class of such programs is derived using machine learning, using the method of reverse motion from known examples of system behavior.

And how easy is it to “understand what is happening” with the help of these various types of modeling? Finding the "exact solution" of mathematical equations is a big plus - then the behavior of the system can be described by an exact mathematical formula. But even when this is not, it is often possible to write down some mathematical statements that are sufficiently abstract so that they can be associated with other systems and behaviors.

As I wrote above, with the program - such as a cellular automaton - everything can be different. Quite often it happens that we are immediately confronted with computational irreducibility, which limits our ability to go through a short way and "explain" what is happening.

What about machine learning and neural networks? In a sense, the training of a neural network is similar to a brief summation of an inductive search going in the natural sciences. We are trying, starting with examples, to derive a model of the behavior of the system. But will it be possible then to understand the model?

And again there are problems with computational irreducibility. But let's discuss the case in which you can imagine what the situation would look like in which we can understand what is happening.

Instead of using a neural network to model the behavior of a system, let's consider the creation of a neural network that classifies a certain aspect of the world: for example, taking an image and distributing them by content (“boat”, “giraffe”, etc.). When we train a neural network, it learns to produce the correct output. But you can potentially imagine this process as an internal construction of a sequence of differences (something like a game of “ twenty questions ”), which ultimately determines the correct conclusion.

But what are these differences? Sometimes we can recognize them. For example, “is there a lot of blue in the picture?” But most of the time these are some properties of the world that people do not notice. Perhaps there is an alternative history of the natural sciences in which some of them would manifest themselves. But they are not part of the current canon of perception or analysis.

If we wanted to add them, we would probably come up with the idea of ​​inventing names for them. But this situation is similar to the situation with logical evidence. The automatic system created some things that it uses as travel milestones to generate the result. But we do not recognize these milestones, they mean nothing to us.

Again, if we found that some specific differences are often found in neural networks, we could decide that they deserve to be explored for us and add them to the standard canon of ways to describe the world.

Can we expect that a small amount of such differences will allow us to create something meaningful? It is like asking whether a small number of theorems will help us to understand such a thing as logical proof.

I think the answer is not clear. If you study, for example, a large collection of scientific papers in mathematics, you can ask questions about the frequency of use of various theorems. It turns out that the frequency of the theorems almost perfectly corresponds to Zipf’s law (and the central limit theorem ,implicit function theorem and Tonelli-Fubini theorem ). The same thing probably happens with differences that “should know”, or new theorems that “should know”.

Knowledge of several theorems will enable us to go far enough, but there will always be an endless exponential tail, and it will not be possible to get to the end.

Future knowledge

Studying mathematics, science, or technology, one can see similar basic ways of qualitative development, consisting in building a set of ever-increasing abstractions. It would be nice to quantify this process. Perhaps you can count how certain terms or descriptions that are often encountered at one time are included in higher levels of abstraction, which in turn have new terms or descriptions associated with them.

It may be possible to create an idealized model of this process with the help of a formal model of computing the type of Turing machines. Imagine that at the lowest level there is a basic Turing machine without abstractions. Now imagine that we choose programs for this Turing machine according to some particular random process. Then we run these programs and analyze them to see which model of a “higher” level of computation can successfully reproduce the joint behavior of these programs without having to execute every step in each of them.

One could decide that computational irreducibility would lead to the fact that creating this higher level computation model would inevitably be more complicated. But the key point is that we are only trying to reproduce the joint behavior of programs, and not their separate behavior.

But what happens if this process is repeated over and over again, reproducing the idealized intellectual history of man and creating a growing tower of abstractions?

Presumably, an analogy can be drawn here with critical phenomena in physics and the renormalization group method . If so, you can imagine that we can determine the trajectory in the platform space for the presentation of concepts. What will this trajectory do?

Perhaps it will have a fixed value, when at any point in the story there is approximately the same number of concepts worth studying - new concepts are slowly opening up and old ones are being absorbed.

What can this mean for mathematics? For example, that any "random mathematical facts", discovered empirically, will eventually be considered when a certain level of abstraction is reached. There is no clear understanding of how this process will work. After all, at any level of abstraction there are always new empirical facts to which we must “jump over”. It may also happen that the "raising the level of abstraction" will move more slowly than is necessary to perform these "jumps".

Future understanding

What does all this mean for the future understanding?

In the past, when people studied nature, they had a small number of reasons for understanding it. Sometimes they personify certain aspects of it in the form of spirits or deities. But they took it for what it is, without thinking about the possibility of understanding all the details of the causes of the processes.

With the advent of modern science — and especially when an increasing majority of our lives are spent in artificial environments dominated by technologies developed by us — these expectations have changed. And when we study the calculations performed by AI, we do not like that we can not understand them.

However, there will always be a competition between what the systems of our world do and what our brains can calculate from their behavior. If we decide to interact only with systems that are much simpler than the brain in computing power, then we can expect that we can systematically understand what they are doing.

But if we want to use all the computational capabilities available in the universe, then inevitably the systems with which we interact will achieve the computational power of our brain. And this means that, according to the principle of computational irreducibility, we can never systematically “overtake” or “understand” the operation of these systems.

But how then can we use them? Well, just like people have always used the system of nature. Of course, we do not know all the details of their work or opportunities. But at some level of abstraction, we know enough to understand how to achieve our goals with their help.

What about areas like math? In mathematics, we are accustomed to the fact that we build a set of our knowledge so that we can understand every step. But experimental mathematics — as well as such possibilities as the automatic proof of theorems — make it obvious that there are areas in which such a method will not be available to us.

Will we call them "mathematics"? I think they should. But this tradition is different from the one to which we are accustomed over the last millennium. We can still create abstractions there, and construct new levels of understanding.

But somewhere in its basis there will be all sorts of different variants of computational non-reducibility, which we can never transfer to the field of human understanding. Something like this happens in the proof of my small axiom of logic. This is an early example of what I think will be one of the main aspects of mathematics - and much more - in the future.