Learning Latency: Queuing Theory
The latency theme over time becomes interesting in different systems in Yandex and beyond. This happens as any guarantees of service appear in these systems. Obviously, the fact is that it is important not only to promise some possibility for users, but also to guarantee its receipt with a reasonable response time. The “rationality” of the response time, of course, varies greatly from one system to another, but the basic principles by which latency manifests itself in all systems are common, and they can be easily considered apart from specificity.
My name is Sergey Trifonov, I work in a team of Real-Time Map Reduce in Yandex. We develop a real-time data streaming platform with second and sub-second response times. The platform is accessible to internal users and allows them to execute application code on constantly incoming data streams. I will try to make a brief overview of the basic concepts of humanity on the subject of latency analysis over the past hundred and ten years, and now we will try to understand what exactly latency can be learned by applying queuing theory.
The phenomenon of latency began to systematically explore, as far as I know, in connection with the advent of queuing systems - telephone networks. The queuing theory began with the work of A. K. Erlang in 1909, in which he showed that the Poisson distribution is applicable to random telephone traffic. Erlang developed a theory that has been used for decades to design telephone networks. The theory allows you to determine the probability of failure in service. For circuit-switched telephone networks, a failure occurred if all channels were busy and the call could not be made. The probability of this event had to be controlled. I wanted to have a guarantee that, for example, 95% of all calls will be served. Erlang's formulas allow you to determine how many servers you need to complete this warranty. if the duration and number of calls is known. In fact, this task is about quality assurance, and today people are still solving similar problems. But systems have become much more complicated. The main problem of the queuing theory is that in most institutions it is not taught, and few people understand the question outside the normal M / M / 1 queue (see about the notationbelow ), but it is well known that life is much more complicated than this system. Therefore, I suggest, bypassing M / M / 1, go directly to the most interesting.
If you do not try to gain complete knowledge of the distribution of probabilities in the system, and focus on simpler questions, you can get interesting and useful results. The most famous of them is, of course, the Little theorem . It is applicable to a system with any input stream, internal device of any complexity and an arbitrary scheduler inside. The only requirement is that the system must be stable: there must be average values of response time and queue length, then they are connected by a simple expression - time average number of requests in the considered part of the system [piece],
- time average number of requests in the considered part of the system [piece],  - the average time for which requests pass through this part of the system [s],
- the average time for which requests pass through this part of the system [s],  - the rate of requests in the system [pcs / s]. The strength of the theorem is that it can be applied to any part of the system: the queue, the performer, the queue + the performer, or the entire network. Often, this theorem is used like this: “The flow of 1Gbit / s flows to us, and we measured the average response time, and it is 10 ms, so we have an average of 1.25 MB in flight”. So, this calculation is not true. More precisely, it is true, only if all requests have the same size in bytes. Little's theorem counts requests in pieces, not in bytes.
- the rate of requests in the system [pcs / s]. The strength of the theorem is that it can be applied to any part of the system: the queue, the performer, the queue + the performer, or the entire network. Often, this theorem is used like this: “The flow of 1Gbit / s flows to us, and we measured the average response time, and it is 10 ms, so we have an average of 1.25 MB in flight”. So, this calculation is not true. More precisely, it is true, only if all requests have the same size in bytes. Little's theorem counts requests in pieces, not in bytes.
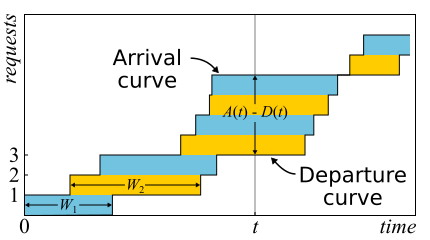 In mathematics it is often necessary to examine the evidence in order to get a real insight. This is the case. Little's theorem is so good that I give a sketch of the proof here. Incoming traffic is described by the function
In mathematics it is often necessary to examine the evidence in order to get a real insight. This is the case. Little's theorem is so good that I give a sketch of the proof here. Incoming traffic is described by the function - the number of requests that have logged in to the point in time
- the number of requests that have logged in to the point in time  . Similarly
. Similarly - the number of requests that left the system at the time
- the number of requests that left the system at the time  . The moment of input (output) of a request is considered the moment of receipt (transmission) of its last byte. The boundaries of the system are determined only by these points in time, so the theorem is obtained widely applicable. If you draw the graphs of these functions in one axis, it is easy to see that
. The moment of input (output) of a request is considered the moment of receipt (transmission) of its last byte. The boundaries of the system are determined only by these points in time, so the theorem is obtained widely applicable. If you draw the graphs of these functions in one axis, it is easy to see that Is the number of requests in the system at time t, and
Is the number of requests in the system at time t, and  - response time of the n-th request.
- response time of the n-th request.
The theorem was formally proved only in 1961, although the relation itself was known long before that.
In fact, if requests within the system can be reordered, then everything is a bit more complicated, so for simplicity we will assume that this does not happen. Although the theorem is true in this case too. Now calculate the area between the graphs. This can be done in two ways. First, on the columns - as is usually considered integrals. In this case, it turns out that the integrand is the size of the queue in pieces. Secondly, line by line - just by adding the latency of all requests. It is clear that both calculations give the same area, therefore they are equal. If both sides of this equality are divided by the time Δt for which we considered the area, then on the left we will have the average queue length (by definition, average). The right is a little harder. It is necessary to insert in the numerator and denominator another number of queries N, then we will
(by definition, average). The right is a little harder. It is necessary to insert in the numerator and denominator another number of queries N, then we will
It is important to say that in the proof we did not use any probability distributions. In fact, Little's theorem is a deterministic law! Such laws are called in the theory of queuing operational law. They can be applied to any parts of the system and to any distributions of all possible random variables. These laws form a constructor that can be successfully used to analyze averages in networks. The disadvantage is that all of them are applicable only to average values and do not give any knowledge about distributions.
Returning to the question why it is impossible to apply Little’s theorem to bytes, suppose and
and  now measured in bytes, not in units. Then, conducting a similar reasoning, we get instead
now measured in bytes, not in units. Then, conducting a similar reasoning, we get instead the weird thing is the area divided by the total number of bytes. This is still seconds, but it is something like weighted average latency, where larger requests get more weight. You can call this value the average latency of the byte - which is, in general, logical, since we replaced the pieces with bytes - but not the latency of the request.
the weird thing is the area divided by the total number of bytes. This is still seconds, but it is something like weighted average latency, where larger requests get more weight. You can call this value the average latency of the byte - which is, in general, logical, since we replaced the pieces with bytes - but not the latency of the request.
Little's theorem says that with a certain flow of requests, the response time and the number of requests in the system are proportional. If all requests look the same, then the average response time cannot be reduced without increasing power. If we know the size of requests in advance, we can try to rearrange them internally to reduce the area between and
and  and, therefore, the average response time of the system. Continuing this thought, one can prove that the Shortest Processing Time and Shortest Remaining Processing Time algorithms provide for a single server the minimum average response time without the possibility of crowding and with it, respectively. But there is a side effect - large requests can not be processed indefinitely. The phenomenon is called “starvation” and is closely related to the concept of fair planning, which can be found in the previous post of Scheduling: myths and reality .
and, therefore, the average response time of the system. Continuing this thought, one can prove that the Shortest Processing Time and Shortest Remaining Processing Time algorithms provide for a single server the minimum average response time without the possibility of crowding and with it, respectively. But there is a side effect - large requests can not be processed indefinitely. The phenomenon is called “starvation” and is closely related to the concept of fair planning, which can be found in the previous post of Scheduling: myths and reality .
There is another common trap associated with understanding the law of Little. There is a single-threaded server that serves user requests. Suppose we somehow measured L - the average number of requests in the queue to this server, and S - the average service time for a single request by the server. Now consider the new incoming request. On average, he sees L requests ahead of him. The maintenance of each of them takes an average of S seconds. It turns out that the average waiting time . But by the theorem it turns out that
. But by the theorem it turns out that . If you equate the expression, we see nonsense:
. If you equate the expression, we see nonsense: . What is wrong with this reasoning?
. What is wrong with this reasoning?
So, Little's theorem can be applied to large and small systems, to queues, to servers and to single processing threads. But in all these cases, requests are usually classified in one way or another. Requests of different users, requests of different priority, requests coming from different locations, or requests of different types. In this case, the aggregated information by classes is not interesting. Yes, the average number of mixed requests and the average response time for all of them are proportional again. But what if we want to know the average response time for a particular class of requests? Surprisingly, Little’s theorem can also be applied to a particular class of queries. In this case, you need to take as rate of requests of this class, but not all. As
rate of requests of this class, but not all. As and
and  - average values of the number and residence time of requests of this class in the studied part of the system.
- average values of the number and residence time of requests of this class in the studied part of the system.
 It is worth noting that for closed systems the “wrong” line of reasoning leads to the conclusion
It is worth noting that for closed systems the “wrong” line of reasoning leads to the conclusion  turns out to be true. Closed systems are those systems in which requests do not come from outside and do not go outside, but circulate inside. Or, alternatively, systems with feedback: as soon as a request leaves the system, a new request takes its place. These systems are also important because any open system can be considered as immersed in a closed system. For example, you can consider a site as an open system, in which requests are constantly pouring in, processed and left, or you can, on the contrary, as a closed system with the entire audience of the site. Then they usually say that the number of users is fixed, and they either wait for the answer to the request, or “think”: they got their page and have not yet clicked on the link. In the event that think time is always zero, the system is also called the batch system.
turns out to be true. Closed systems are those systems in which requests do not come from outside and do not go outside, but circulate inside. Or, alternatively, systems with feedback: as soon as a request leaves the system, a new request takes its place. These systems are also important because any open system can be considered as immersed in a closed system. For example, you can consider a site as an open system, in which requests are constantly pouring in, processed and left, or you can, on the contrary, as a closed system with the entire audience of the site. Then they usually say that the number of users is fixed, and they either wait for the answer to the request, or “think”: they got their page and have not yet clicked on the link. In the event that think time is always zero, the system is also called the batch system.
Little's law for closed systems is fair if the speed of external arrivals (they are not in a closed system) replaced by the system bandwidth. If we wrap the single-threaded server, discussed above, into a batch system, we get
(they are not in a closed system) replaced by the system bandwidth. If we wrap the single-threaded server, discussed above, into a batch system, we get and recycling 100%. Often this view of the system gives unexpected results. In the 90s, it was this consideration of the Internet together with users as a single system that gave impetus to the study of distributions other than exponential. We will discuss the distributions further, but here we note that at that time almost everything and everywhere was regarded as exponential, and even found some justification for this, and not just an excuse in the spirit of "otherwise too complicated." However, it turned out that not all practically important distributions have equally long tails, and knowledge of tails of distribution can be tried. But for now let us return to the average values.
and recycling 100%. Often this view of the system gives unexpected results. In the 90s, it was this consideration of the Internet together with users as a single system that gave impetus to the study of distributions other than exponential. We will discuss the distributions further, but here we note that at that time almost everything and everywhere was regarded as exponential, and even found some justification for this, and not just an excuse in the spirit of "otherwise too complicated." However, it turned out that not all practically important distributions have equally long tails, and knowledge of tails of distribution can be tried. But for now let us return to the average values.
Suppose we have an open system: a complex network or a simple single-threaded server is not important. What will change if we speed up the arrival of requests twice and speed up their processing twice - for example, having doubled the power of all the system components? How will the utilization, throughput, average number of requests in the system and the average response time change? For a single-threaded server, you can try to take the formulas, apply them "in the forehead" and get the results, but what to do with an arbitrary network? Intuitive solution is as follows. Suppose that time has doubled in speed, then in our “accelerated reference system” the speed of servers and the flow of requests did not seem to change; accordingly, all parameters in accelerated time have the same values as before. In other words, the acceleration of all the “moving parts” of any system is equivalent to the acceleration of a clock. Now convert the values to a system with normal time. The dimensionless quantities (utilization and average number of requests) will not change. Values whose dimension includes time multipliers of the first degree will change proportionally. The bandwidth [requests / s] will double, and the response and wait time [s] will be halved.
This result can be interpreted in two ways:
Once again, I note that this is true for a wide class of systems, and not just for a simple server. From a practical point of view, there are only two problems:
Consider the limit. Suppose, in the same open system, interpretation No. 2. We divide each incoming request in half. The response time is also divided in half. Repeat the division many times. And we do not even need to change anything in the system. It turns out that the response time can be made arbitrarily small by simply cutting incoming requests into a sufficiently large number of parts. In the limit, we can say that instead of requests, we get a “request fluid”, which we filter with our servers. This is the so-called fluid model, a very convenient tool for simplified analysis. But why is the response time zero? Something went wrong? In which place we did not take into account the latency? It turns out that we did not take into account the speed of light, it can not be doubled. The propagation time in the network channel cannot be changed; you can only accept it. In fact, transmission through the network includes two components: transmission time (propagation time) and propagation time (propagation time). The first can be accelerated by increasing the power (channel width) or reducing the size of the packets, and the second is very difficult to influence. In our “liquid model” there were no reservoirs for the accumulation of liquids - network channels with non-zero and constant propagation times. By the way, if we add them to our “fluid model”, the latency will be determined by the sum of propagation times, and the queues at the nodes will still be empty. Queues depend only on the size of the packets and the variability (read burst) of the input stream. and the second is very difficult to influence. In our “liquid model” there were no reservoirs for the accumulation of liquids - network channels with non-zero and constant propagation times. By the way, if we add them to our “fluid model”, the latency will be determined by the sum of propagation times, and the queues at the nodes will still be empty. Queues depend only on the size of the packets and the variability (read burst) of the input stream. and the second is very difficult to influence. In our “liquid model” there were no reservoirs for the accumulation of liquids - network channels with non-zero and constant propagation times. By the way, if we add them to our “fluid model”, the latency will be determined by the sum of propagation times, and the queues at the nodes will still be empty. Queues depend only on the size of the packets and the variability (read burst) of the input stream.
It follows from this that if we are talking about latency, it is impossible to get by with the flow calculations, and even the disposal of devices does not solve everything. It is necessary to take into account the size of requests and not to forget about the propagation time, which is often ignored in queuing theory, although it is not at all difficult to add it to the calculations.
What is the general reason for the formation of queues? Obviously, there is not enough capacity in the system, and the excess of requests accumulates? Wrong! Queues also occur in systems where resources are sufficient. If there is not enough power, then the system, as the theorists say, is not stable. There are two main reasons for the formation of queues: the irregularity of the receipt of requests and the variability of the size of requests. We have already considered an example in which both of these reasons were eliminated: a real-time system, where requests of the same size come strictly periodically. The queue is never formed. The average waiting time in the queue is zero. It is clear that to achieve this behavior is very difficult, if not impossible, and therefore queues are formed. Queuing theory is based on the assumption
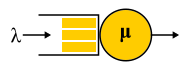
 For the description of different systems used Kendall notation A / S / k / K, where A is the distribution of time between requests, S is the size distribution of requests, k is the number of servers, K is the limit on the simultaneous number of requests in the system (omitted if there is no limit). For example, the well-known M / M / 1 is decoded as follows: the first M (Markovian or Memoryless) means that a Poisson flow of problems is fed to the system. Read: messages come at random times with a given average speed.
For the description of different systems used Kendall notation A / S / k / K, where A is the distribution of time between requests, S is the size distribution of requests, k is the number of servers, K is the limit on the simultaneous number of requests in the system (omitted if there is no limit). For example, the well-known M / M / 1 is decoded as follows: the first M (Markovian or Memoryless) means that a Poisson flow of problems is fed to the system. Read: messages come at random times with a given average speed. requests per second - just like radioactive decay - or, more formally: the time between two neighboring events has an exponential distribution. The second M indicates that the service for these messages also has an exponential distribution and, on average, μ requests are processed per second. Finally, a one at the end indicates that maintenance is performed by a single server. The queue is not limited, since the 4th part of the notation is absent. The letters used in this notation are rather strangely chosen: G is an arbitrary distribution (no, not Gaussian, as one might think), D is deterministic. Real-time system - D / D / 1. The first queuing theory system that Erlang decided in 1909 is M / D / 1. But the analytic unresolved system so far is M / G / k for k> 1, and the solution for M / G / 1 was found back in 1930.
requests per second - just like radioactive decay - or, more formally: the time between two neighboring events has an exponential distribution. The second M indicates that the service for these messages also has an exponential distribution and, on average, μ requests are processed per second. Finally, a one at the end indicates that maintenance is performed by a single server. The queue is not limited, since the 4th part of the notation is absent. The letters used in this notation are rather strangely chosen: G is an arbitrary distribution (no, not Gaussian, as one might think), D is deterministic. Real-time system - D / D / 1. The first queuing theory system that Erlang decided in 1909 is M / D / 1. But the analytic unresolved system so far is M / G / k for k> 1, and the solution for M / G / 1 was found back in 1930.
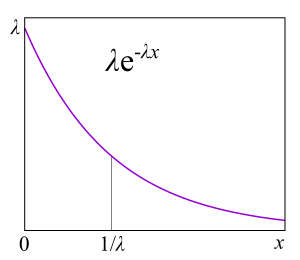 The main reason is that they do almost any task about the queue being solved, because, as we will see later, it is possible to apply Markov chains, about which mathematicians already know a lot of things. Exponential distributions have many good properties for a theory because they do not have memory. I will not give here the definition of this property, for developers it will be more useful to explain through failure rate. Suppose you have a certain device, but from practice you know the distribution of the lifetime of such devices: they often fail at the beginning of life, then break relatively rarely and after the warranty period expires, they often begin to break again. Formally, this information is precisely contained in the failure rate function, which is quite simply associated with the distribution. In fact, this is the “aligned” probability density given that the device has survived to a certain point. From a practical point of view, this is exactly what we are interested in: the frequency of device failures as a function of the time they are already in operation. For example, if the failure rate is a constant, that is, the failure rate of a device does not depend on the time of operation, and failures just happen randomly with some frequency, then the distribution of the lifetime of the device is exponential. In this case, in order to predict how long the device will work, you do not need to know how long it has been in operation, what wear and tear it has, and whatever else. This is the "lack of memory."
The main reason is that they do almost any task about the queue being solved, because, as we will see later, it is possible to apply Markov chains, about which mathematicians already know a lot of things. Exponential distributions have many good properties for a theory because they do not have memory. I will not give here the definition of this property, for developers it will be more useful to explain through failure rate. Suppose you have a certain device, but from practice you know the distribution of the lifetime of such devices: they often fail at the beginning of life, then break relatively rarely and after the warranty period expires, they often begin to break again. Formally, this information is precisely contained in the failure rate function, which is quite simply associated with the distribution. In fact, this is the “aligned” probability density given that the device has survived to a certain point. From a practical point of view, this is exactly what we are interested in: the frequency of device failures as a function of the time they are already in operation. For example, if the failure rate is a constant, that is, the failure rate of a device does not depend on the time of operation, and failures just happen randomly with some frequency, then the distribution of the lifetime of the device is exponential. In this case, in order to predict how long the device will work, you do not need to know how long it has been in operation, what wear and tear it has, and whatever else. This is the "lack of memory."
Failure rate can be calculated for any distribution. In the theory of queuing - for the distribution of the query execution time. Failure rate says how long the request will still be executed, based on how much it is already running. If we have an increasing failure rate, then the longer the request is executed, the greater the likelihood that it will end soon. If we have a decreasing failure rate, then the longer the request is executed, the greater the likelihood that it will be executed even longer. What do you think, which of these two options is most typical for computing systems, databases and other things related to software and hardware? For a start: why is this important at all? An example from everyday life. You are standing in line at the cashier, at first the queue is moving well, but at some point it stops moving. Should I move to another queue of the same length? If the service has an exponential distribution, then the answer is no difference. In the case of a distribution with a heavy tail (decreasing failure rate) it may be beneficial to migrate to another queue. This kind of "situation analysis"can be used for balancing or migrating processes.
It turns out that in production more frequent distributions are either exponential or with an increasing failure rate, while in computer systems, on the contrary, the execution times of all requests or unix processes have distributions with a heavy tail. This is quite unexpected news, and I decided to check it out.
RTMR performs many different application code on data that is created from search user sessions. I armed myself with LWTrace and traced all the necessary data from our production cluster. I was only interested in the time of the user code. Streaming processing occurs fairly quickly, so it was not difficult for me to collect data on about a million randomly selected launches on random machines within a few hours. Since I was interested in the distribution tail, I plotted the distribution in double logarithmic axes. To understand the increasing or decreasing failure rate has this distribution, I compared it with two other distributions that have exactly the same mean value: exponential and Pareto distribution.
in double logarithmic axes. To understand the increasing or decreasing failure rate has this distribution, I compared it with two other distributions that have exactly the same mean value: exponential and Pareto distribution.
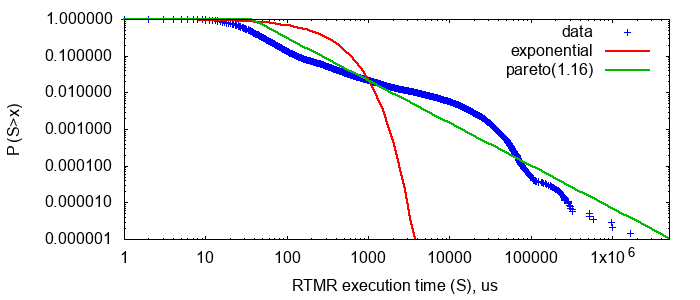
Pareto distribution has a power form , and therefore decays more slowly than any exponent - it has a heavy tail. It is also famous for the fact that it is often found in the “wild nature”, the 80/20 principle: the distribution of wealth in society, file sizes on the Internet, etc. In the double logarithmic axes, it turns into a straight line, which is very convenient for comparison by eye. As you can see, in RTMR we have something more like Pareto than an exponent. Parameter
, and therefore decays more slowly than any exponent - it has a heavy tail. It is also famous for the fact that it is often found in the “wild nature”, the 80/20 principle: the distribution of wealth in society, file sizes on the Internet, etc. In the double logarithmic axes, it turns into a straight line, which is very convenient for comparison by eye. As you can see, in RTMR we have something more like Pareto than an exponent. Parameter That corresponds to the 80/20 principle: only 20% of requests create 80% of the load.
That corresponds to the 80/20 principle: only 20% of requests create 80% of the load.
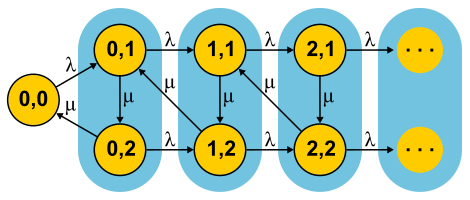
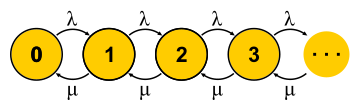 This big topic is impossible to embrace a couple of paragraphs, but I will try. Markov chains allow you to look at the finite state machine from a probabilistic point of view. For this purpose, it is assumed that events that change the state of the automaton are random and the automaton simply transitions between states with some known probabilities. For queuing theory, an automaton is used whose states are the number of requests in the system. The event “new request” puts the machine into the next state, and the event “end of service” returns it. The question is: what will happen if we allow enough time for such an automaton? Suppose many such automata exist in parallel (an ensemble of automata, if you like), and they independently and randomly float from one state to another. Now consider a state, for example state 0 in the figure.
This big topic is impossible to embrace a couple of paragraphs, but I will try. Markov chains allow you to look at the finite state machine from a probabilistic point of view. For this purpose, it is assumed that events that change the state of the automaton are random and the automaton simply transitions between states with some known probabilities. For queuing theory, an automaton is used whose states are the number of requests in the system. The event “new request” puts the machine into the next state, and the event “end of service” returns it. The question is: what will happen if we allow enough time for such an automaton? Suppose many such automata exist in parallel (an ensemble of automata, if you like), and they independently and randomly float from one state to another. Now consider a state, for example state 0 in the figure. was balanced by the speed of transitions to other states
was balanced by the speed of transitions to other states  . Thus, we get the equations as many as the unknowns - by the number of states. Then we solve the system and find the so-called equilibrium distribution. For each individual automaton, this distribution says what proportion of the time in which state it is. A short juggling with symbols leads for M / M / 1 to a result.
. Thus, we get the equations as many as the unknowns - by the number of states. Then we solve the system and find the so-called equilibrium distribution. For each individual automaton, this distribution says what proportion of the time in which state it is. A short juggling with symbols leads for M / M / 1 to a result. where
where  - this is server recycling. The end of the story. In the course of the presentation, I missed a decent amount of assumptions and made a couple of substitutions for the concepts, but I hope I didn’t suffer the essence.
- this is server recycling. The end of the story. In the course of the presentation, I missed a decent amount of assumptions and made a couple of substitutions for the concepts, but I hope I didn’t suffer the essence.
It is important to understand that this approach works only if the current state of the machine fully determines its further behavior, and the story of how it got into this state is not important. For everyday understanding of a finite state machine, this goes without saying - after all, it is a state of it. But for the stochastic process it follows from this that all distributions must be exponential, since only they do not have memory — they have a constant failure rate.
 It is also important to say that all other information about the system is easy to obtain if we know the equilibrium distribution. The average number of queries in the system is the average value of this distribution. To find out the average response time, we apply the Little theorem to the number of queries. The distribution of response time is a little more difficult to find, but also in a few steps you can find out that
It is also important to say that all other information about the system is easy to obtain if we know the equilibrium distribution. The average number of queries in the system is the average value of this distribution. To find out the average response time, we apply the Little theorem to the number of queries. The distribution of response time is a little more difficult to find, but also in a few steps you can find out that and what is the average response time
and what is the average response time  .
.
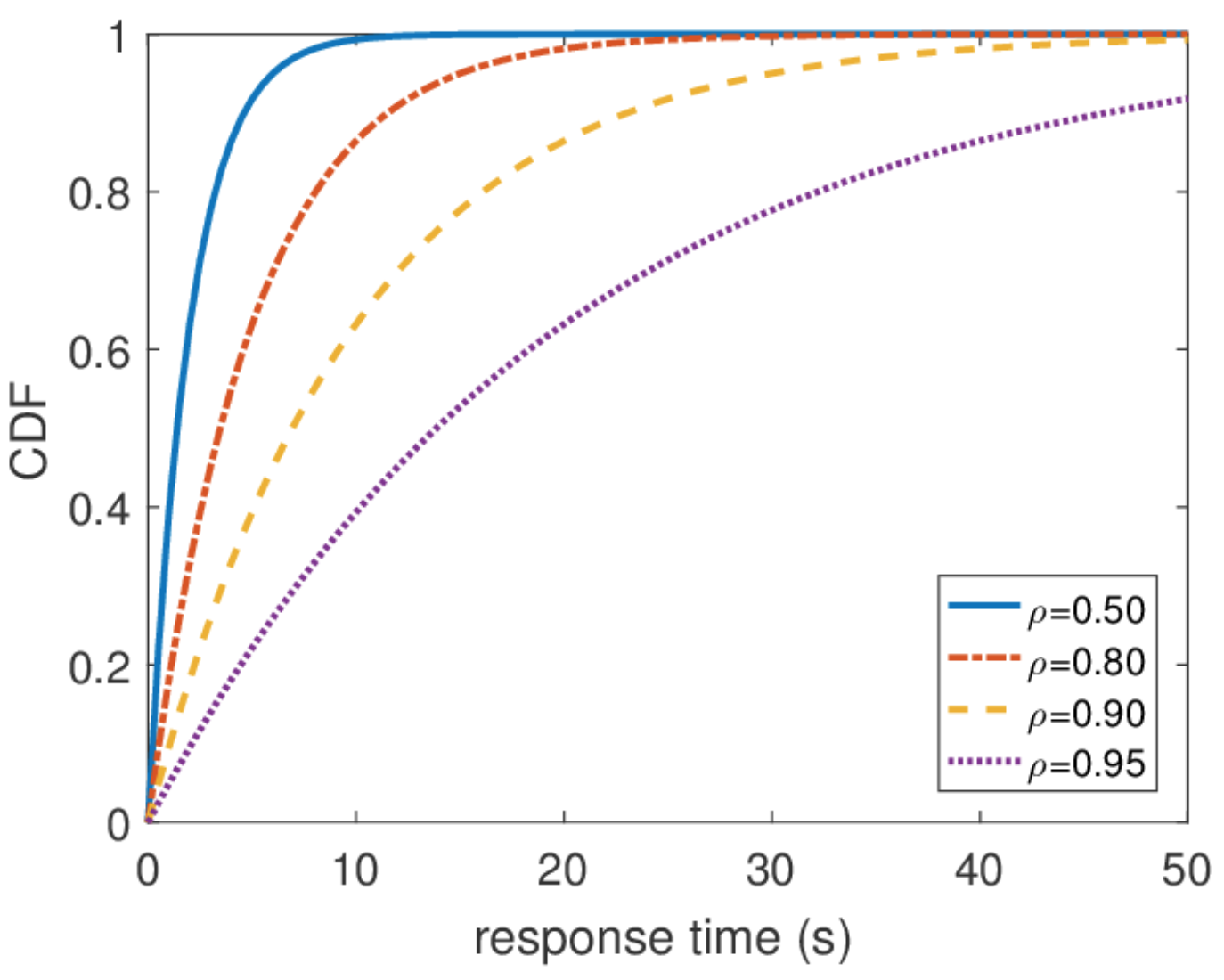
By this distribution, you can find any percentile response time, and it turns out that the hundredth percentile is equal to infinity. In other words, the worst response time is not limited from above. That, in general, is not surprising, since we used the Poisson flow. But in practice, this behavior can never occur. Obviously, the input stream of requests to the server is limited, at least by the width of the network channel to this server, and the queue length by the memory on this server. A Poisson flow, on the contrary, with a nonzero probability guarantees the occurrence of arbitrarily large bursts. Therefore, I would not recommend, when designing a system, to proceed from the assumption of a Poisson input stream, if you are interested in high percentiles, and the system load is very high. It is better to use other traffic models, about which I will talk about another time,
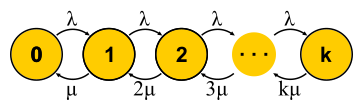 Now that we have at our disposal a powerful enough way to analyze systems, we can try to apply it to different tasks and reap the benefits. Something like this developed the theory of queuing in the second half of the twentieth century. Let's try to understand what was achieved. To begin, let us return to the problems that Erlang solved. These are the tasks M / M / k / k and M / M / k in which we would like to limit the probability of failure. It turns out that it is easy for them to build Markov chains. The difference is that as you add tasks, the probability of a reverse transition increases as tasks begin to be processed in parallel, but when the number of tasks becomes equal to the number of servers, saturation occurs. Further for M / M / k / k the network ends, the automaton is indeed finite, and all requests that come to the last state are rejected.
Now that we have at our disposal a powerful enough way to analyze systems, we can try to apply it to different tasks and reap the benefits. Something like this developed the theory of queuing in the second half of the twentieth century. Let's try to understand what was achieved. To begin, let us return to the problems that Erlang solved. These are the tasks M / M / k / k and M / M / k in which we would like to limit the probability of failure. It turns out that it is easy for them to build Markov chains. The difference is that as you add tasks, the probability of a reverse transition increases as tasks begin to be processed in parallel, but when the number of tasks becomes equal to the number of servers, saturation occurs. Further for M / M / k / k the network ends, the automaton is indeed finite, and all requests that come to the last state are rejected.
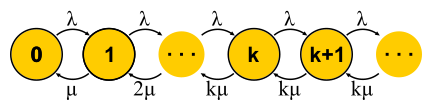 For M / M / k, the situation is more complicated, requests are queuing, new states appear, but the probability of a reverse transition does not increase — all the servers are already running. The network becomes infinite, as for M / M / 1. By the way, if the number of requests in the system is limited, then the chain will always have a finite number of states and one way or another will be solved, which cannot be said about endless chains. In closed systems, the chains are always finite. Solving the described chains for M / M / k / k and M / M / k, we come to formula B and formula CErlang respectively. They are rather cumbersome, I will not give them, but with their help you can get an interesting result for the development of intuition, which is called square root staffing rule. Suppose there is a system M / M / k with some given input flow λ requests per second. Suppose that the load should double tomorrow. The question is: how to increase the number of servers, so that the response time remains the same? The number of servers must be doubled, right? It turns out not at all. Recall what we have already seen: if we speed up time (servers and input) by half, then the average response time will be halved. A few slow and one fast server are not the same thing, but nevertheless the processing power is the same. In particular, for M / M / 1, for example, the response time is inversely proportional to the volume of “free capacity”
For M / M / k, the situation is more complicated, requests are queuing, new states appear, but the probability of a reverse transition does not increase — all the servers are already running. The network becomes infinite, as for M / M / 1. By the way, if the number of requests in the system is limited, then the chain will always have a finite number of states and one way or another will be solved, which cannot be said about endless chains. In closed systems, the chains are always finite. Solving the described chains for M / M / k / k and M / M / k, we come to formula B and formula CErlang respectively. They are rather cumbersome, I will not give them, but with their help you can get an interesting result for the development of intuition, which is called square root staffing rule. Suppose there is a system M / M / k with some given input flow λ requests per second. Suppose that the load should double tomorrow. The question is: how to increase the number of servers, so that the response time remains the same? The number of servers must be doubled, right? It turns out not at all. Recall what we have already seen: if we speed up time (servers and input) by half, then the average response time will be halved. A few slow and one fast server are not the same thing, but nevertheless the processing power is the same. In particular, for M / M / 1, for example, the response time is inversely proportional to the volume of “free capacity” and is determined only by this volume. With an increase in both the flow and the computing power by half, the free capacity of the system doubles:
and is determined only by this volume. With an increase in both the flow and the computing power by half, the free capacity of the system doubles: . It may seem that to solve the problem you just need to keep the free capacity, but the response time in M / M / k is determined already by a more complex Erlang formula. It turns out that the free capacity must be maintained in proportion to the square root of the number of “busy servers” in order to maintain the previous response time. By the number of “busy servers” is meant the total number of servers multiplied by utilization: this is the minimum number of servers required for stable operation.
. It may seem that to solve the problem you just need to keep the free capacity, but the response time in M / M / k is determined already by a more complex Erlang formula. It turns out that the free capacity must be maintained in proportion to the square root of the number of “busy servers” in order to maintain the previous response time. By the number of “busy servers” is meant the total number of servers multiplied by utilization: this is the minimum number of servers required for stable operation.
Using this rule, sometimes they try to justify how to expand the cluster with servers. But you should not have the illusion that any cluster is an M / M / k-system. For example, if you have a balancer in your input that sends requests in the queue to the servers, this is no longer M / M / k, since M / M / k implies a common queue from which servers take requests when they are released. But this model is suitable, for example, for trade-outs with a common FIFO queue. However, even in this case, it is worth remembering that this rule is an approximation for the case when there are a lot of threads. In fact, if you have more than 10 threads, you can safely assume that there are a lot of them. Well, do not forget about the ubiquitous exponential distributions: without the assumption that all distributions are exponential, the rule also does not work.
Ultimately, of interest is a network of M / M / k, connected at least in a chain, as we do distributed systems. To study the networks I would like to have a constructor: simple and clear rules for connecting known elements into blocks. In control theory, for example, there are transfer functions that are combined in an understandable way with serial or parallel connections. Here, the output stream from any node has a very complex distribution, with the exception of M / M / k, which, according to the well-known theorem of Burke, produces an independent Poisson flow. This exception, as you can guess, is mainly used.
The connection of two Poisson flows is a Poisson flow. Probabilistic separation of a Poisson flow into two - again gives two Poisson flows. All this leads to the fact that all the queues in the system seem to be independent, and you can get, to put it in a formal language, the so-called product-form solution . That is, the joint distribution of queue lengths is simply the product of the length distributions of all the queues considered separately - this is how independence is expressed in probability theory. Just find the input streams to all nodes and use the formulas for each node independently. There are a number of limitations:
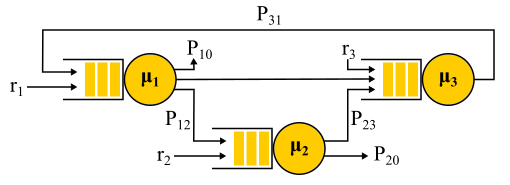 An example of the Jackson network.
An example of the Jackson network.
It should be noted that in the presence of feedback the Poisson flow is NOT obtained, since the flows turn out to be interdependent. At the exit from the node with feedback, a non-Poisson flow is also obtained, and as a result, all flows become non-Poisson. However, surprisingly, it turns out that all these non-Poisson flows behave exactly the same as the Poisson flows (oh, this probability theory), if the above limitations are satisfied. And then we again get the product-form solution. Such networks are called Jackson networks., in them are possible feedbacks and, therefore, multiple visits to any server. There are other networks in which more liberties are allowed, but as a result all the significant analytical achievements of queuing theory in relation to networks imply Poisson flows at the entrance and a product-form solution, which became the subject of criticism of this theory and led in the 90s to the development of other theories, as well as to the study of which distributions are actually needed and how to work with them.
An important application of this whole theory of Jackson networks is the modeling of packets in IP networks and ATM networks. The model is quite adequate: the packet sizes do not change much and do not depend on the packet itself, only on the channel width, since the service time corresponds to the packet transmission time to the channel. Random time of sending, although it sounds crazy, in fact, has not very large variability. Moreover, it turns out that in a network with a deterministic service time, the latency cannot be greater than in a similar Jackson network, so such networks can be safely used to estimate the response time from above.
All the results that I talked about were exponential distributions, but I also mentioned that real distributions are different. There is a feeling that this whole theory is quite useless. This is not quite true. There is a way to build in this mathematical apparatus and other distributions, moreover, almost any distributions, but it will cost us something. With the exception of a few interesting cases, the opportunity to get a solution is lost explicitly, the product-form solution is lost, and with it the constructor: each task must be solved entirely from scratch using Markov chains. For theory, this is a big problem, but in practice it simply means the use of numerical methods and makes it possible to solve much more complex and realistic problems.
The idea is simple. Markov chains do not allow us to have a memory within one state, so all transitions must be random with an exponential distribution of time between two transitions. But what if the state is divided into several substates? As before, transitions between substates must have an exponential distribution if we want the whole construction to remain a Markov chain, and we really want it, because we know how to solve such chains. Substates are often called phases, if they are arranged sequentially, and the partitioning process is called the phase method.
The simplest example. The processing of the request is carried out in several phases: first, for example, we read the necessary data from the database, then we perform some calculations, then we write the results into the database. Suppose all these three stages have the same exponential distribution of time. What is the distribution time of the passage of all three phases together? This is the Erlang distribution.
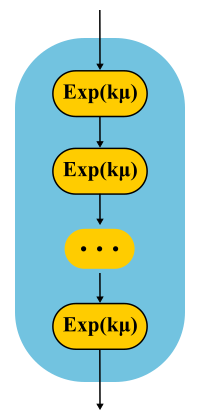
And what if you make many, many short identical phases? In the limit, we obtain a deterministic distribution. That is, building a chain, you can reduce the variability of the distribution.
Is it possible to increase the variability? Easy. Instead of a chain of phases, we use alternative categories, randomly choosing one of them. Example. Almost all requests are executed quickly, but there is a small chance that there will be a huge request that is executed for a long time. Such a distribution will have a decreasing failure rate. The longer we wait, the greater the likelihood that the request falls into the second category.

Continuing to develop the phase method, theorists found that there is a class of distributions, with which you can approach with any accuracy an arbitrary non-negative distribution! Coxian distibution is built using the phase method, only we do not have to go through all the phases, there is some probability of completion after each phase.
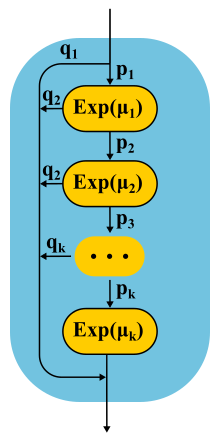
Such distributions can be used both to generate a non-Poisson input stream and to create a non-exponential service time. Here, for example, the Markov chain for the M / E2 / 1 system with Erlang distribution for service time. The state is determined by a pair of numbers (n, s), where n is the queue length, and s is the number of the stage in which the server is located: first or second. All combinations of n and s are possible. Incoming messages change only n, and upon completion of the phases they alternate and the queue length decreases after the completion of the second phase.
Can a system loaded at half its capacity slow down? As the first experimental, we prepare M / G / 1. Given: Poisson flow at the input and arbitrary distribution of service time. Consider the path of a single request through the entire system. Incoming incoming request sees the average number of requests in a queue in front of it![$ \ mathbf {E} [N_Q] $](https://habrastorage.org/getpro/habr/formulas/2b3/15f/8f1/2b315f8f114054ebaab5c5555e670d3a.svg) . The average processing time of each of them
. The average processing time of each of them![$ \ mathbf {E} [S] $](https://habrastorage.org/getpro/habr/formulas/9c5/9ef/289/9c59ef2892bff977cc035db99ceee803.svg) . With probability equal to recycling
. With probability equal to recycling , there is one more request in the server, which you need to first “finish” in time
, there is one more request in the server, which you need to first “finish” in time ![$ \ mathbf {E} [S_e] $](https://habrastorage.org/getpro/habr/formulas/2b8/cc6/71b/2b8cc671b30499feb76a0e79c39ca912.svg) . Summing up, we get that the total waiting time in the queue
. Summing up, we get that the total waiting time in the queue![$ \ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e] $](https://habrastorage.org/getpro/habr/formulas/5b1/c31/1ca/5b1c311caad51431e9d4c3edfeefc5b4.svg) . By Little's theorem
. By Little's theorem![$ \ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q] $](https://habrastorage.org/getpro/habr/formulas/c7d/43e/c3c/c7d43ec3c94792e84a5547f03ac2c2cc.svg) ; combining, we get:
; combining, we get: , sees that it takes time to pre-service
, sees that it takes time to pre-service  .
.

Average time![$ \ mathbf {E} [S_e] $](https://habrastorage.org/getpro/habr/formulas/2b8/cc6/71b/2b8cc671b30499feb76a0e79c39ca912.svg) determined by the average value of the function
determined by the average value of the function  , that is, the area of the triangles divided by the total time. It is clear that we can confine ourselves to one "middle" triangle, then
, that is, the area of the triangles divided by the total time. It is clear that we can confine ourselves to one "middle" triangle, then![$ \ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S] $](https://habrastorage.org/getpro/habr/formulas/6af/f06/c3b/6aff06c3b5b8198ce7e3367620dbf899.svg) . This is quite unexpected. We have received that the time of after-service is determined not only by the average value of the service time, but also by its variability. The explanation is simple. The probability of falling into a long interval
. This is quite unexpected. We have received that the time of after-service is determined not only by the average value of the service time, but also by its variability. The explanation is simple. The probability of falling into a long interval more, it is actually proportional to the duration S of this interval. This explains the famous Waiting Time Paradox, or Inspection Paradox. But back to M / G / 1. If you combine everything that we have received and rewrite using the variability
more, it is actually proportional to the duration S of this interval. This explains the famous Waiting Time Paradox, or Inspection Paradox. But back to M / G / 1. If you combine everything that we have received and rewrite using the variability![$ С ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2 $](https://habrastorage.org/getpro/habr/formulas/90e/7b9/d1c/90e7b9d1cee5e1caabeb5f0157accac7.svg) , we get the famous formula Pollaczek-Khinchine :
, we get the famous formula Pollaczek-Khinchine : . This, you will agree, is much more than
. This, you will agree, is much more than for exponential distribution. On average, everything is super fast:
for exponential distribution. On average, everything is super fast:![$ \ mathbf {E} [S] = 263.792 μs $](https://habrastorage.org/getpro/habr/formulas/75c/8de/6d5/75c8de6d5ce163c6b3b8169d8fe9b416.svg) . Now suppose that RTMR is modeled by the system M / G / 1, and let the system not be heavily loaded, the recycling
. Now suppose that RTMR is modeled by the system M / G / 1, and let the system not be heavily loaded, the recycling . Substituting in the formula, we get
. Substituting in the formula, we get![$ \ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263.792 μs = 50 ms $](https://habrastorage.org/getpro/habr/formulas/eef/9ed/9ef/eef9ed9efd45544d7cc3067eb0fe67e6.svg) . Due to microbursts, even such a fast and under-utilized system can turn into an average disgusting one. For 50 ms, you can go to the hard drive 6 times or, if you're lucky, even to a data center on another continent! By the way, for G / G / 1 there is an approximation that takes into account the variability of incoming traffic: it looks exactly the same, only instead
. Due to microbursts, even such a fast and under-utilized system can turn into an average disgusting one. For 50 ms, you can go to the hard drive 6 times or, if you're lucky, even to a data center on another continent! By the way, for G / G / 1 there is an approximation that takes into account the variability of incoming traffic: it looks exactly the same, only instead in it the sum of both variations
in it the sum of both variations  . For a case with several servers, things are better, but the effect of several servers only affects the first multiplier. The effect of variability remains:
. For a case with several servers, things are better, but the effect of several servers only affects the first multiplier. The effect of variability remains:![$ \ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2 $](https://habrastorage.org/getpro/habr/formulas/cd7/c93/12f/cd7c9312ff51914db8e8bf0388053cfc.svg) .
.
What do microbursts look like? In the case of trade-offs, these are tasks that are serviced fast enough so as not to be noticeable on the disposal schedules, and slowly enough to create a queue behind them and influence the response time of the pool. From the point of view of theory, these are huge requests from the tail part of the distribution. Let's say you have a pool of 10 threads, and you look at the recycling schedule, built on the metrics of working time and downtime, which are collected every 15 seconds. First, you may not notice that one thread generally hung, or that all 10 threads performed large tasks at the same time for a whole second, and then did nothing for 14 seconds. A resolution of 15 seconds does not allow to see a utilization jump of up to 100% and back to 0%, and the response time suffers. For example, this may look like microbirst,
As a microscope, a trace system is used that records the time of events (receipt and completion of requests) with an accuracy of processor cycles.
Especially to deal with such situations, the RTMR uses the SelfPing mechanism, which periodically (every 10 ms) sends a small task to the trappool for the sole purpose of measuring the waiting time in the queue. Assuming the worst case, a period of 10 ms is added to this measurement and a maximum of 15 seconds is taken on the window. Thus, we get the upper estimate for the maximum waiting time on the window. Yes, we do not see the real situation if the response time is less than 10 ms, but in this case we can assume that everything is fine - there is not a single microbearst. But this additional self-ping activity eats a strictly limited amount of CPU. The mechanism is convenient in that it is universal and non-invasive: you do not need to change either the code of the trample or the code of the tasks that are executed in it. I emphasize: it is the worst case that is measured which is very convenient and intuitive, compared with all sorts of percentiles. Also, the mechanism detects another similar situation: the simultaneous arrival of a large number of quite ordinary requests. If there are not so many of them, so that the problem can be seen on the 15-second disposal schedules, this can also be considered microbird.
Well, what if SelfPing shows that something is inadequate? How to find the guilty? To do this, we use the trace already mentioned by LWTrace. We go to the problem machine and, through monitoring, we launch a trace, which keeps track of all the tasks in the right route and keeps only the slow ones in memory. Then you can see the top 100 slow runs. After a short study, turn off the trace. All other ways of searching for the guilty are not suitable: it is impossible to write logs for all the tasks of a trappool; writing only slow tasks is also not the best solution, since you still have to collect the track for all tasks, and this is also expensive; profiling with perf does not help, since heavy tasks happen too rarely to be visible in a profile.
 We still have one more “degree of freedom”, which we have not used so far. We discussed the incoming flow and request sizes, different numbers of servers, too, but have not yet talked about schedulers. All examples implied FIFO processing. As I already mentioned, scheduling does affect the response time of the system, and the correct scheduler can significantly improve latency (SPT and SRPT algorithms). But planning is a very advanced topic for queuing theory. Perhaps this theory is not even very well suited for the study of planners, but this is the only theory that can provide answers to prochastic systems with planners and allows us to calculate averages. There are other theories that allow you to understand a lot about planning “at worst”, but we'll talk about them another time.
We still have one more “degree of freedom”, which we have not used so far. We discussed the incoming flow and request sizes, different numbers of servers, too, but have not yet talked about schedulers. All examples implied FIFO processing. As I already mentioned, scheduling does affect the response time of the system, and the correct scheduler can significantly improve latency (SPT and SRPT algorithms). But planning is a very advanced topic for queuing theory. Perhaps this theory is not even very well suited for the study of planners, but this is the only theory that can provide answers to prochastic systems with planners and allows us to calculate averages. There are other theories that allow you to understand a lot about planning “at worst”, but we'll talk about them another time.
And now let's consider some interesting exceptions from the general rule, when you still manage to get a product-form solution for the network and you can create a convenient constructor. Let's start with one M / Cox / 1 / PS node. Poisson flow at the entrance, almost arbitrary distribution (Coxian distribution) of service time and fair scheduler (Processor Sharing), serving all requests at the same time, but with a speed inversely proportional to their current number. Where can I find such a system? For example, this is how fair process planners work in operating systems. At first glance it may seem that this is a complex system, but if you build (see the method section of the phases) and decide the corresponding Markov chain, it turns out that the distribution of the queue length exactly repeats the M / M / 1 / FIFO system , in which the service time has the same mean value, but is distributed exponentially.
This is an incredible result! In contrast to what we saw in the section on microbyls, here the variability of the service time does not affect the response time in any of the percentiles! This property is rare and is called insensitivity property. Usually it occurs in systems where there is no waiting, and the request immediately starts to be executed in one way or another, when you do not need to wait for the additional service of what is already being performed. Another example of a system with this property is M / M / ∞. It also has no waiting, as the number of servers is infinite. In such systems, the output stream from the node has a good distribution, which allows us to obtain a product-form solution for networks with such servers — BCMP networks .
 For completeness, consider the simplest example. Two servers operating at different average speeds (for example, the processor frequency is different), an arbitrary distribution of the sizes of incoming tasks, the service server is chosen randomly, most of the tasks go to the fast server. We need to find the average response time. Decision.
For completeness, consider the simplest example. Two servers operating at different average speeds (for example, the processor frequency is different), an arbitrary distribution of the sizes of incoming tasks, the service server is chosen randomly, most of the tasks go to the fast server. We need to find the average response time. Decision.![$ \ mathbf {E} [T] = 1/3 \ mathbf {E} [T_1] + 2/3 \ mathbf {E} [T_2] $](https://habrastorage.org/getpro/habr/formulas/9e8/a28/2e2/9e8a282e23452a27025daec9a7f77fa3.svg) . Apply the well-known formula
. Apply the well-known formula![$ \ mathbf {E} [T_i] = 1 / (\ mu_i - \ lambda_i) $](https://habrastorage.org/getpro/habr/formulas/861/21d/7e5/86121d7e5dfa192b2aac9f1b71608b5f.svg) for the average response time M / M / 1 / FCFS and get
for the average response time M / M / 1 / FCFS and get ![$ \ mathbf {E} [T] = 1/3 * 1 / (3 - 3 * 1/3) + 2/3 * 1 / (4 - 3 * 2/3) = 0.5 with $](https://habrastorage.org/getpro/habr/formulas/db3/f78/065/db3f78065b10a9e731f9e5750bde5de6.svg) .
.
That's all, now and planning discussed, you can wrap up. In the next article, I will discuss how real-time systems approach the issue of latency and what concepts are used there.
My name is Sergey Trifonov, I work in a team of Real-Time Map Reduce in Yandex. We develop a real-time data streaming platform with second and sub-second response times. The platform is accessible to internal users and allows them to execute application code on constantly incoming data streams. I will try to make a brief overview of the basic concepts of humanity on the subject of latency analysis over the past hundred and ten years, and now we will try to understand what exactly latency can be learned by applying queuing theory.
The phenomenon of latency began to systematically explore, as far as I know, in connection with the advent of queuing systems - telephone networks. The queuing theory began with the work of A. K. Erlang in 1909, in which he showed that the Poisson distribution is applicable to random telephone traffic. Erlang developed a theory that has been used for decades to design telephone networks. The theory allows you to determine the probability of failure in service. For circuit-switched telephone networks, a failure occurred if all channels were busy and the call could not be made. The probability of this event had to be controlled. I wanted to have a guarantee that, for example, 95% of all calls will be served. Erlang's formulas allow you to determine how many servers you need to complete this warranty. if the duration and number of calls is known. In fact, this task is about quality assurance, and today people are still solving similar problems. But systems have become much more complicated. The main problem of the queuing theory is that in most institutions it is not taught, and few people understand the question outside the normal M / M / 1 queue (see about the notationbelow ), but it is well known that life is much more complicated than this system. Therefore, I suggest, bypassing M / M / 1, go directly to the most interesting.
Average values
If you do not try to gain complete knowledge of the distribution of probabilities in the system, and focus on simpler questions, you can get interesting and useful results. The most famous of them is, of course, the Little theorem . It is applicable to a system with any input stream, internal device of any complexity and an arbitrary scheduler inside. The only requirement is that the system must be stable: there must be average values of response time and queue length, then they are connected by a simple expression
How to use Little's theorem
 In mathematics it is often necessary to examine the evidence in order to get a real insight. This is the case. Little's theorem is so good that I give a sketch of the proof here. Incoming traffic is described by the function
In mathematics it is often necessary to examine the evidence in order to get a real insight. This is the case. Little's theorem is so good that I give a sketch of the proof here. Incoming traffic is described by the functionThe theorem was formally proved only in 1961, although the relation itself was known long before that.
In fact, if requests within the system can be reordered, then everything is a bit more complicated, so for simplicity we will assume that this does not happen. Although the theorem is true in this case too. Now calculate the area between the graphs. This can be done in two ways. First, on the columns - as is usually considered integrals. In this case, it turns out that the integrand is the size of the queue in pieces. Secondly, line by line - just by adding the latency of all requests. It is clear that both calculations give the same area, therefore they are equal. If both sides of this equality are divided by the time Δt for which we considered the area, then on the left we will have the average queue length
It is important to say that in the proof we did not use any probability distributions. In fact, Little's theorem is a deterministic law! Such laws are called in the theory of queuing operational law. They can be applied to any parts of the system and to any distributions of all possible random variables. These laws form a constructor that can be successfully used to analyze averages in networks. The disadvantage is that all of them are applicable only to average values and do not give any knowledge about distributions.
Returning to the question why it is impossible to apply Little’s theorem to bytes, suppose
Little's theorem says that with a certain flow of requests, the response time and the number of requests in the system are proportional. If all requests look the same, then the average response time cannot be reduced without increasing power. If we know the size of requests in advance, we can try to rearrange them internally to reduce the area between
There is another common trap associated with understanding the law of Little. There is a single-threaded server that serves user requests. Suppose we somehow measured L - the average number of requests in the queue to this server, and S - the average service time for a single request by the server. Now consider the new incoming request. On average, he sees L requests ahead of him. The maintenance of each of them takes an average of S seconds. It turns out that the average waiting time
- The first thing that catches the eye: the response time by the theorem does not depend on S. In fact, of course, it depends. Simply, the average queue length already takes this into account: the faster the server, the shorter the queue length and the shorter the response time.
- We consider a system in which the queues do not accumulate forever, but are regularly reset. This means that server utilization is less than 100% and we skip all incoming requests, and with the same average speed with which these requests came, which means, on average, processing one request takes not S seconds, but more
seconds, simply because sometimes we do not process any requests. The fact is that in any stable open system without loss the throughput does not depend on the speed of the servers, it is determined only by the input stream.
- The assumption that an incoming request sees the average number of requests in the system is not always true. A counterexample: incoming requests come strictly periodically, and we manage to process each request before the next one arrives. Typical picture for real-time systems. An incoming request always sees in the system zero requests, but on average in the system, obviously, more than zero requests. If requests come at completely random times, then they really “see the average number of requests” .

- We did not take into account that with some probability there can already be one request in the server that needs to be “re-served”. In general, the average “after-service” time differs from the initial service time, and sometimes, paradoxically , it can be much longer. We will return to this question at the end, when we discuss microbursts, stay tuned.
So, Little's theorem can be applied to large and small systems, to queues, to servers and to single processing threads. But in all these cases, requests are usually classified in one way or another. Requests of different users, requests of different priority, requests coming from different locations, or requests of different types. In this case, the aggregated information by classes is not interesting. Yes, the average number of mixed requests and the average response time for all of them are proportional again. But what if we want to know the average response time for a particular class of requests? Surprisingly, Little’s theorem can also be applied to a particular class of queries. In this case, you need to take as
Open and closed systems
 It is worth noting that for closed systems the “wrong” line of reasoning leads to the conclusion
It is worth noting that for closed systems the “wrong” line of reasoning leads to the conclusion Little's law for closed systems is fair if the speed of external arrivals
Relativistic effects
Suppose we have an open system: a complex network or a simple single-threaded server is not important. What will change if we speed up the arrival of requests twice and speed up their processing twice - for example, having doubled the power of all the system components? How will the utilization, throughput, average number of requests in the system and the average response time change? For a single-threaded server, you can try to take the formulas, apply them "in the forehead" and get the results, but what to do with an arbitrary network? Intuitive solution is as follows. Suppose that time has doubled in speed, then in our “accelerated reference system” the speed of servers and the flow of requests did not seem to change; accordingly, all parameters in accelerated time have the same values as before. In other words, the acceleration of all the “moving parts” of any system is equivalent to the acceleration of a clock. Now convert the values to a system with normal time. The dimensionless quantities (utilization and average number of requests) will not change. Values whose dimension includes time multipliers of the first degree will change proportionally. The bandwidth [requests / s] will double, and the response and wait time [s] will be halved.
This result can be interpreted in two ways:
- Accelerated k times the system can digest the flow of tasks k times more, and with an average response time k times less.
- We can say that the power has not changed, but simply the size of the tasks has decreased by k times. It turns out that we are sending the same load to the system, but sawn into smaller pieces. And ... lo and behold! The average response time decreases!
Once again, I note that this is true for a wide class of systems, and not just for a simple server. From a practical point of view, there are only two problems:
- Not all parts of the system can be easily accelerated. For some, we can not affect in any way at all. For example, at the speed of light.
- Not all tasks can be infinitely divided into smaller ones, since they have not learned to transfer information in portions of less than one bit.
Consider the limit. Suppose, in the same open system, interpretation No. 2. We divide each incoming request in half. The response time is also divided in half. Repeat the division many times. And we do not even need to change anything in the system. It turns out that the response time can be made arbitrarily small by simply cutting incoming requests into a sufficiently large number of parts. In the limit, we can say that instead of requests, we get a “request fluid”, which we filter with our servers. This is the so-called fluid model, a very convenient tool for simplified analysis. But why is the response time zero? Something went wrong? In which place we did not take into account the latency? It turns out that we did not take into account the speed of light, it can not be doubled. The propagation time in the network channel cannot be changed; you can only accept it. In fact, transmission through the network includes two components: transmission time (propagation time) and propagation time (propagation time). The first can be accelerated by increasing the power (channel width) or reducing the size of the packets, and the second is very difficult to influence. In our “liquid model” there were no reservoirs for the accumulation of liquids - network channels with non-zero and constant propagation times. By the way, if we add them to our “fluid model”, the latency will be determined by the sum of propagation times, and the queues at the nodes will still be empty. Queues depend only on the size of the packets and the variability (read burst) of the input stream. and the second is very difficult to influence. In our “liquid model” there were no reservoirs for the accumulation of liquids - network channels with non-zero and constant propagation times. By the way, if we add them to our “fluid model”, the latency will be determined by the sum of propagation times, and the queues at the nodes will still be empty. Queues depend only on the size of the packets and the variability (read burst) of the input stream. and the second is very difficult to influence. In our “liquid model” there were no reservoirs for the accumulation of liquids - network channels with non-zero and constant propagation times. By the way, if we add them to our “fluid model”, the latency will be determined by the sum of propagation times, and the queues at the nodes will still be empty. Queues depend only on the size of the packets and the variability (read burst) of the input stream.
It follows from this that if we are talking about latency, it is impossible to get by with the flow calculations, and even the disposal of devices does not solve everything. It is necessary to take into account the size of requests and not to forget about the propagation time, which is often ignored in queuing theory, although it is not at all difficult to add it to the calculations.
Distributions
What is the general reason for the formation of queues? Obviously, there is not enough capacity in the system, and the excess of requests accumulates? Wrong! Queues also occur in systems where resources are sufficient. If there is not enough power, then the system, as the theorists say, is not stable. There are two main reasons for the formation of queues: the irregularity of the receipt of requests and the variability of the size of requests. We have already considered an example in which both of these reasons were eliminated: a real-time system, where requests of the same size come strictly periodically. The queue is never formed. The average waiting time in the queue is zero. It is clear that to achieve this behavior is very difficult, if not impossible, and therefore queues are formed. Queuing theory is based on the assumption
 For the description of different systems used Kendall notation A / S / k / K, where A is the distribution of time between requests, S is the size distribution of requests, k is the number of servers, K is the limit on the simultaneous number of requests in the system (omitted if there is no limit). For example, the well-known M / M / 1 is decoded as follows: the first M (Markovian or Memoryless) means that a Poisson flow of problems is fed to the system. Read: messages come at random times with a given average speed.
For the description of different systems used Kendall notation A / S / k / K, where A is the distribution of time between requests, S is the size distribution of requests, k is the number of servers, K is the limit on the simultaneous number of requests in the system (omitted if there is no limit). For example, the well-known M / M / 1 is decoded as follows: the first M (Markovian or Memoryless) means that a Poisson flow of problems is fed to the system. Read: messages come at random times with a given average speed.Why use exponential distributions?
 The main reason is that they do almost any task about the queue being solved, because, as we will see later, it is possible to apply Markov chains, about which mathematicians already know a lot of things. Exponential distributions have many good properties for a theory because they do not have memory. I will not give here the definition of this property, for developers it will be more useful to explain through failure rate. Suppose you have a certain device, but from practice you know the distribution of the lifetime of such devices: they often fail at the beginning of life, then break relatively rarely and after the warranty period expires, they often begin to break again. Formally, this information is precisely contained in the failure rate function, which is quite simply associated with the distribution. In fact, this is the “aligned” probability density given that the device has survived to a certain point. From a practical point of view, this is exactly what we are interested in: the frequency of device failures as a function of the time they are already in operation. For example, if the failure rate is a constant, that is, the failure rate of a device does not depend on the time of operation, and failures just happen randomly with some frequency, then the distribution of the lifetime of the device is exponential. In this case, in order to predict how long the device will work, you do not need to know how long it has been in operation, what wear and tear it has, and whatever else. This is the "lack of memory."
The main reason is that they do almost any task about the queue being solved, because, as we will see later, it is possible to apply Markov chains, about which mathematicians already know a lot of things. Exponential distributions have many good properties for a theory because they do not have memory. I will not give here the definition of this property, for developers it will be more useful to explain through failure rate. Suppose you have a certain device, but from practice you know the distribution of the lifetime of such devices: they often fail at the beginning of life, then break relatively rarely and after the warranty period expires, they often begin to break again. Formally, this information is precisely contained in the failure rate function, which is quite simply associated with the distribution. In fact, this is the “aligned” probability density given that the device has survived to a certain point. From a practical point of view, this is exactly what we are interested in: the frequency of device failures as a function of the time they are already in operation. For example, if the failure rate is a constant, that is, the failure rate of a device does not depend on the time of operation, and failures just happen randomly with some frequency, then the distribution of the lifetime of the device is exponential. In this case, in order to predict how long the device will work, you do not need to know how long it has been in operation, what wear and tear it has, and whatever else. This is the "lack of memory."Short and long tails
Failure rate can be calculated for any distribution. In the theory of queuing - for the distribution of the query execution time. Failure rate says how long the request will still be executed, based on how much it is already running. If we have an increasing failure rate, then the longer the request is executed, the greater the likelihood that it will end soon. If we have a decreasing failure rate, then the longer the request is executed, the greater the likelihood that it will be executed even longer. What do you think, which of these two options is most typical for computing systems, databases and other things related to software and hardware? For a start: why is this important at all? An example from everyday life. You are standing in line at the cashier, at first the queue is moving well, but at some point it stops moving. Should I move to another queue of the same length? If the service has an exponential distribution, then the answer is no difference. In the case of a distribution with a heavy tail (decreasing failure rate) it may be beneficial to migrate to another queue. This kind of "situation analysis"can be used for balancing or migrating processes.
It turns out that in production more frequent distributions are either exponential or with an increasing failure rate, while in computer systems, on the contrary, the execution times of all requests or unix processes have distributions with a heavy tail. This is quite unexpected news, and I decided to check it out.
RTMR performs many different application code on data that is created from search user sessions. I armed myself with LWTrace and traced all the necessary data from our production cluster. I was only interested in the time of the user code. Streaming processing occurs fairly quickly, so it was not difficult for me to collect data on about a million randomly selected launches on random machines within a few hours. Since I was interested in the distribution tail, I plotted the distribution

Pareto distribution has a power form
Markov chains
 This big topic is impossible to embrace a couple of paragraphs, but I will try. Markov chains allow you to look at the finite state machine from a probabilistic point of view. For this purpose, it is assumed that events that change the state of the automaton are random and the automaton simply transitions between states with some known probabilities. For queuing theory, an automaton is used whose states are the number of requests in the system. The event “new request” puts the machine into the next state, and the event “end of service” returns it. The question is: what will happen if we allow enough time for such an automaton? Suppose many such automata exist in parallel (an ensemble of automata, if you like), and they independently and randomly float from one state to another. Now consider a state, for example state 0 in the figure.
This big topic is impossible to embrace a couple of paragraphs, but I will try. Markov chains allow you to look at the finite state machine from a probabilistic point of view. For this purpose, it is assumed that events that change the state of the automaton are random and the automaton simply transitions between states with some known probabilities. For queuing theory, an automaton is used whose states are the number of requests in the system. The event “new request” puts the machine into the next state, and the event “end of service” returns it. The question is: what will happen if we allow enough time for such an automaton? Suppose many such automata exist in parallel (an ensemble of automata, if you like), and they independently and randomly float from one state to another. Now consider a state, for example state 0 in the figure.It is important to understand that this approach works only if the current state of the machine fully determines its further behavior, and the story of how it got into this state is not important. For everyday understanding of a finite state machine, this goes without saying - after all, it is a state of it. But for the stochastic process it follows from this that all distributions must be exponential, since only they do not have memory — they have a constant failure rate.
 It is also important to say that all other information about the system is easy to obtain if we know the equilibrium distribution. The average number of queries in the system is the average value of this distribution. To find out the average response time, we apply the Little theorem to the number of queries. The distribution of response time is a little more difficult to find, but also in a few steps you can find out that
It is also important to say that all other information about the system is easy to obtain if we know the equilibrium distribution. The average number of queries in the system is the average value of this distribution. To find out the average response time, we apply the Little theorem to the number of queries. The distribution of response time is a little more difficult to find, but also in a few steps you can find out thatUnlimited response time
By this distribution, you can find any percentile response time, and it turns out that the hundredth percentile is equal to infinity. In other words, the worst response time is not limited from above. That, in general, is not surprising, since we used the Poisson flow. But in practice, this behavior can never occur. Obviously, the input stream of requests to the server is limited, at least by the width of the network channel to this server, and the queue length by the memory on this server. A Poisson flow, on the contrary, with a nonzero probability guarantees the occurrence of arbitrarily large bursts. Therefore, I would not recommend, when designing a system, to proceed from the assumption of a Poisson input stream, if you are interested in high percentiles, and the system load is very high. It is better to use other traffic models, about which I will talk about another time,
Scaling and Warranties
 Now that we have at our disposal a powerful enough way to analyze systems, we can try to apply it to different tasks and reap the benefits. Something like this developed the theory of queuing in the second half of the twentieth century. Let's try to understand what was achieved. To begin, let us return to the problems that Erlang solved. These are the tasks M / M / k / k and M / M / k in which we would like to limit the probability of failure. It turns out that it is easy for them to build Markov chains. The difference is that as you add tasks, the probability of a reverse transition increases as tasks begin to be processed in parallel, but when the number of tasks becomes equal to the number of servers, saturation occurs. Further for M / M / k / k the network ends, the automaton is indeed finite, and all requests that come to the last state are rejected.
Now that we have at our disposal a powerful enough way to analyze systems, we can try to apply it to different tasks and reap the benefits. Something like this developed the theory of queuing in the second half of the twentieth century. Let's try to understand what was achieved. To begin, let us return to the problems that Erlang solved. These are the tasks M / M / k / k and M / M / k in which we would like to limit the probability of failure. It turns out that it is easy for them to build Markov chains. The difference is that as you add tasks, the probability of a reverse transition increases as tasks begin to be processed in parallel, but when the number of tasks becomes equal to the number of servers, saturation occurs. Further for M / M / k / k the network ends, the automaton is indeed finite, and all requests that come to the last state are rejected. For M / M / k, the situation is more complicated, requests are queuing, new states appear, but the probability of a reverse transition does not increase — all the servers are already running. The network becomes infinite, as for M / M / 1. By the way, if the number of requests in the system is limited, then the chain will always have a finite number of states and one way or another will be solved, which cannot be said about endless chains. In closed systems, the chains are always finite. Solving the described chains for M / M / k / k and M / M / k, we come to formula B and formula CErlang respectively. They are rather cumbersome, I will not give them, but with their help you can get an interesting result for the development of intuition, which is called square root staffing rule. Suppose there is a system M / M / k with some given input flow λ requests per second. Suppose that the load should double tomorrow. The question is: how to increase the number of servers, so that the response time remains the same? The number of servers must be doubled, right? It turns out not at all. Recall what we have already seen: if we speed up time (servers and input) by half, then the average response time will be halved. A few slow and one fast server are not the same thing, but nevertheless the processing power is the same. In particular, for M / M / 1, for example, the response time is inversely proportional to the volume of “free capacity”
For M / M / k, the situation is more complicated, requests are queuing, new states appear, but the probability of a reverse transition does not increase — all the servers are already running. The network becomes infinite, as for M / M / 1. By the way, if the number of requests in the system is limited, then the chain will always have a finite number of states and one way or another will be solved, which cannot be said about endless chains. In closed systems, the chains are always finite. Solving the described chains for M / M / k / k and M / M / k, we come to formula B and formula CErlang respectively. They are rather cumbersome, I will not give them, but with their help you can get an interesting result for the development of intuition, which is called square root staffing rule. Suppose there is a system M / M / k with some given input flow λ requests per second. Suppose that the load should double tomorrow. The question is: how to increase the number of servers, so that the response time remains the same? The number of servers must be doubled, right? It turns out not at all. Recall what we have already seen: if we speed up time (servers and input) by half, then the average response time will be halved. A few slow and one fast server are not the same thing, but nevertheless the processing power is the same. In particular, for M / M / 1, for example, the response time is inversely proportional to the volume of “free capacity”Using this rule, sometimes they try to justify how to expand the cluster with servers. But you should not have the illusion that any cluster is an M / M / k-system. For example, if you have a balancer in your input that sends requests in the queue to the servers, this is no longer M / M / k, since M / M / k implies a common queue from which servers take requests when they are released. But this model is suitable, for example, for trade-outs with a common FIFO queue. However, even in this case, it is worth remembering that this rule is an approximation for the case when there are a lot of threads. In fact, if you have more than 10 threads, you can safely assume that there are a lot of them. Well, do not forget about the ubiquitous exponential distributions: without the assumption that all distributions are exponential, the rule also does not work.
Online response time
Ultimately, of interest is a network of M / M / k, connected at least in a chain, as we do distributed systems. To study the networks I would like to have a constructor: simple and clear rules for connecting known elements into blocks. In control theory, for example, there are transfer functions that are combined in an understandable way with serial or parallel connections. Here, the output stream from any node has a very complex distribution, with the exception of M / M / k, which, according to the well-known theorem of Burke, produces an independent Poisson flow. This exception, as you can guess, is mainly used.
The connection of two Poisson flows is a Poisson flow. Probabilistic separation of a Poisson flow into two - again gives two Poisson flows. All this leads to the fact that all the queues in the system seem to be independent, and you can get, to put it in a formal language, the so-called product-form solution . That is, the joint distribution of queue lengths is simply the product of the length distributions of all the queues considered separately - this is how independence is expressed in probability theory. Just find the input streams to all nodes and use the formulas for each node independently. There are a number of limitations:
- Probabilistic routing algorithm. A query served by a node chooses the next one with a certain probability. This is not as bad as it may seem, because it is possible to use the “request classes”: say that all Vasya requests come to server No. 1, then to server No. 2, and then go out of the network, and Petit's requests come to server No. 2 , and then with equal probability they visit server No. 1 or No. 3 and exit. That is, not all transitions are required to be random, some or even all may have a 100% probability.
- The assumption of independence of Kleinrock. The processing time of the request cannot depend on the history or class of the request, but is determined only by the server, and when the request is repeated through the same server, it is randomly selected each time. In fact, there is no possibility to set the size of the request that would be used in different servers, and the service time is determined only by the server itself. This restriction can also be circumvented. For this purpose, probabilistic routing is usually used and a loop is made to return to the same server with a certain probability, as if restarting the request. In my opinion, this is a rather strange trick, because such a request re-enters the queue, and is not executed immediately, but for some tasks this is not important.
- Poisson input traffic and exponential service time on all nodes.

It should be noted that in the presence of feedback the Poisson flow is NOT obtained, since the flows turn out to be interdependent. At the exit from the node with feedback, a non-Poisson flow is also obtained, and as a result, all flows become non-Poisson. However, surprisingly, it turns out that all these non-Poisson flows behave exactly the same as the Poisson flows (oh, this probability theory), if the above limitations are satisfied. And then we again get the product-form solution. Such networks are called Jackson networks., in them are possible feedbacks and, therefore, multiple visits to any server. There are other networks in which more liberties are allowed, but as a result all the significant analytical achievements of queuing theory in relation to networks imply Poisson flows at the entrance and a product-form solution, which became the subject of criticism of this theory and led in the 90s to the development of other theories, as well as to the study of which distributions are actually needed and how to work with them.
An important application of this whole theory of Jackson networks is the modeling of packets in IP networks and ATM networks. The model is quite adequate: the packet sizes do not change much and do not depend on the packet itself, only on the channel width, since the service time corresponds to the packet transmission time to the channel. Random time of sending, although it sounds crazy, in fact, has not very large variability. Moreover, it turns out that in a network with a deterministic service time, the latency cannot be greater than in a similar Jackson network, so such networks can be safely used to estimate the response time from above.
Nonexponential distribution
All the results that I talked about were exponential distributions, but I also mentioned that real distributions are different. There is a feeling that this whole theory is quite useless. This is not quite true. There is a way to build in this mathematical apparatus and other distributions, moreover, almost any distributions, but it will cost us something. With the exception of a few interesting cases, the opportunity to get a solution is lost explicitly, the product-form solution is lost, and with it the constructor: each task must be solved entirely from scratch using Markov chains. For theory, this is a big problem, but in practice it simply means the use of numerical methods and makes it possible to solve much more complex and realistic problems.
Phase method
The idea is simple. Markov chains do not allow us to have a memory within one state, so all transitions must be random with an exponential distribution of time between two transitions. But what if the state is divided into several substates? As before, transitions between substates must have an exponential distribution if we want the whole construction to remain a Markov chain, and we really want it, because we know how to solve such chains. Substates are often called phases, if they are arranged sequentially, and the partitioning process is called the phase method.
The simplest example. The processing of the request is carried out in several phases: first, for example, we read the necessary data from the database, then we perform some calculations, then we write the results into the database. Suppose all these three stages have the same exponential distribution of time. What is the distribution time of the passage of all three phases together? This is the Erlang distribution.

And what if you make many, many short identical phases? In the limit, we obtain a deterministic distribution. That is, building a chain, you can reduce the variability of the distribution.
Is it possible to increase the variability? Easy. Instead of a chain of phases, we use alternative categories, randomly choosing one of them. Example. Almost all requests are executed quickly, but there is a small chance that there will be a huge request that is executed for a long time. Such a distribution will have a decreasing failure rate. The longer we wait, the greater the likelihood that the request falls into the second category.

Continuing to develop the phase method, theorists found that there is a class of distributions, with which you can approach with any accuracy an arbitrary non-negative distribution! Coxian distibution is built using the phase method, only we do not have to go through all the phases, there is some probability of completion after each phase.

Such distributions can be used both to generate a non-Poisson input stream and to create a non-exponential service time. Here, for example, the Markov chain for the M / E2 / 1 system with Erlang distribution for service time. The state is determined by a pair of numbers (n, s), where n is the queue length, and s is the number of the stage in which the server is located: first or second. All combinations of n and s are possible. Incoming messages change only n, and upon completion of the phases they alternate and the queue length decreases after the completion of the second phase.

You have microburst!
Can a system loaded at half its capacity slow down? As the first experimental, we prepare M / G / 1. Given: Poisson flow at the input and arbitrary distribution of service time. Consider the path of a single request through the entire system. Incoming incoming request sees the average number of requests in a queue in front of it

Average time
What do microbursts look like? In the case of trade-offs, these are tasks that are serviced fast enough so as not to be noticeable on the disposal schedules, and slowly enough to create a queue behind them and influence the response time of the pool. From the point of view of theory, these are huge requests from the tail part of the distribution. Let's say you have a pool of 10 threads, and you look at the recycling schedule, built on the metrics of working time and downtime, which are collected every 15 seconds. First, you may not notice that one thread generally hung, or that all 10 threads performed large tasks at the same time for a whole second, and then did nothing for 14 seconds. A resolution of 15 seconds does not allow to see a utilization jump of up to 100% and back to 0%, and the response time suffers. For example, this may look like microbirst,

As a microscope, a trace system is used that records the time of events (receipt and completion of requests) with an accuracy of processor cycles.
Especially to deal with such situations, the RTMR uses the SelfPing mechanism, which periodically (every 10 ms) sends a small task to the trappool for the sole purpose of measuring the waiting time in the queue. Assuming the worst case, a period of 10 ms is added to this measurement and a maximum of 15 seconds is taken on the window. Thus, we get the upper estimate for the maximum waiting time on the window. Yes, we do not see the real situation if the response time is less than 10 ms, but in this case we can assume that everything is fine - there is not a single microbearst. But this additional self-ping activity eats a strictly limited amount of CPU. The mechanism is convenient in that it is universal and non-invasive: you do not need to change either the code of the trample or the code of the tasks that are executed in it. I emphasize: it is the worst case that is measured which is very convenient and intuitive, compared with all sorts of percentiles. Also, the mechanism detects another similar situation: the simultaneous arrival of a large number of quite ordinary requests. If there are not so many of them, so that the problem can be seen on the 15-second disposal schedules, this can also be considered microbird.
Well, what if SelfPing shows that something is inadequate? How to find the guilty? To do this, we use the trace already mentioned by LWTrace. We go to the problem machine and, through monitoring, we launch a trace, which keeps track of all the tasks in the right route and keeps only the slow ones in memory. Then you can see the top 100 slow runs. After a short study, turn off the trace. All other ways of searching for the guilty are not suitable: it is impossible to write logs for all the tasks of a trappool; writing only slow tasks is also not the best solution, since you still have to collect the track for all tasks, and this is also expensive; profiling with perf does not help, since heavy tasks happen too rarely to be visible in a profile.
Independence from service time allocation
 We still have one more “degree of freedom”, which we have not used so far. We discussed the incoming flow and request sizes, different numbers of servers, too, but have not yet talked about schedulers. All examples implied FIFO processing. As I already mentioned, scheduling does affect the response time of the system, and the correct scheduler can significantly improve latency (SPT and SRPT algorithms). But planning is a very advanced topic for queuing theory. Perhaps this theory is not even very well suited for the study of planners, but this is the only theory that can provide answers to prochastic systems with planners and allows us to calculate averages. There are other theories that allow you to understand a lot about planning “at worst”, but we'll talk about them another time.
We still have one more “degree of freedom”, which we have not used so far. We discussed the incoming flow and request sizes, different numbers of servers, too, but have not yet talked about schedulers. All examples implied FIFO processing. As I already mentioned, scheduling does affect the response time of the system, and the correct scheduler can significantly improve latency (SPT and SRPT algorithms). But planning is a very advanced topic for queuing theory. Perhaps this theory is not even very well suited for the study of planners, but this is the only theory that can provide answers to prochastic systems with planners and allows us to calculate averages. There are other theories that allow you to understand a lot about planning “at worst”, but we'll talk about them another time.And now let's consider some interesting exceptions from the general rule, when you still manage to get a product-form solution for the network and you can create a convenient constructor. Let's start with one M / Cox / 1 / PS node. Poisson flow at the entrance, almost arbitrary distribution (Coxian distribution) of service time and fair scheduler (Processor Sharing), serving all requests at the same time, but with a speed inversely proportional to their current number. Where can I find such a system? For example, this is how fair process planners work in operating systems. At first glance it may seem that this is a complex system, but if you build (see the method section of the phases) and decide the corresponding Markov chain, it turns out that the distribution of the queue length exactly repeats the M / M / 1 / FIFO system , in which the service time has the same mean value, but is distributed exponentially.
This is an incredible result! In contrast to what we saw in the section on microbyls, here the variability of the service time does not affect the response time in any of the percentiles! This property is rare and is called insensitivity property. Usually it occurs in systems where there is no waiting, and the request immediately starts to be executed in one way or another, when you do not need to wait for the additional service of what is already being performed. Another example of a system with this property is M / M / ∞. It also has no waiting, as the number of servers is infinite. In such systems, the output stream from the node has a good distribution, which allows us to obtain a product-form solution for networks with such servers — BCMP networks .
 For completeness, consider the simplest example. Two servers operating at different average speeds (for example, the processor frequency is different), an arbitrary distribution of the sizes of incoming tasks, the service server is chosen randomly, most of the tasks go to the fast server. We need to find the average response time. Decision.
For completeness, consider the simplest example. Two servers operating at different average speeds (for example, the processor frequency is different), an arbitrary distribution of the sizes of incoming tasks, the service server is chosen randomly, most of the tasks go to the fast server. We need to find the average response time. Decision.That's all, now and planning discussed, you can wrap up. In the next article, I will discuss how real-time systems approach the issue of latency and what concepts are used there.
What to read and see
- The study of queuing theory is always accompanied by a rather keen mathematics, and often the systems that are considered have nothing to do with computer science, therefore it is difficult to find a good textbook. I would recommend Performance Modeling and Design of Computer Systems (2013). There is still enough mathematics, but all of it is attached to interesting systems. Most of this article is a free retelling of this book.
- The simplest, to the extent possible, without loss of meaning, is the presentation of the classics of the theory about which I know, in the format of video lectures of Robert B. Cooper. In these lectures, he very lucidly tells almost his entire book and all that is required for its understanding.
