Elimination of perspective distortions and straightening of curved lines in photos of book spreads
Last time, in the article “Searching for the spine line in photographs of book spreads,” we promised to talk about what happens with a photograph of a book spread after that, namely, about eliminating perspective distortions and straightening curved lines of text. Without this, getting OCR quality results is almost impossible.
So, we believe that we have already found the spine line in the photograph, we will use this knowledge to determine the vanishing points for the reversal pages ( vanishing point) Vanish points are points of convergence of parallel lines in a perspective projection of a book onto the image plane. Both of them should be located on the continuation of this line, but for each of the pages the position of the point may be different. This is shown schematically in the following illustration (in fact, this is a log for debugging). The spine line is highlighted in red, the lines intersecting at the vanish points are green.
As a rule, the vanish points of two pages are not far from each other, but the above example shows that this does not always happen: for the left page of this spread, the green lines converge very weakly and the vanish point lies far below, and for the right - at the top, relatively close to the edge of the image.
How can I find these lines in the image? Again, the Hough transform (Hough transform ), only the image we need to prepare for this accordingly. We will try to highlight the boundaries of text blocks in the image in the simplest possible way. To do this, we perform the following simple steps:
1) Binarization;
2) Normalization of the image in size, for example, up to 800 pixels on the long side;
3) Morphological building (dilation, r = 6);
4) Morphological gradient (r = 1).
If we apply the fast Hough transform to the resulting image, we get:
Several local maxima corresponding to the borders of pages and text blocks are clearly distinguishable on it. The root line divides these sets into two (let us call them “left” and “right”, respectively), and each of them is well described by a line in Hough space. As you know, lines in Hough's space correspond to points in the image space. These are the desired vanish points.
To search for lines in Hough space, it is proposed to first select local maxima using the non-maximum suppression algorithm. We discard all maxima weaker than 0.2 of the largest. In principle, noise can be filtered in a different way, it is important to leave only points corresponding to fairly long contours in the gradient image. The group of maxima from the neighborhood of the point corresponding to the root line (it is highlighted in red at the beginning of the article), we average and add the center of this cluster to the “left” and “right” sets of points with increased weight. We use the least squares method ( OLS) to search for lines describing our sets of points (in the figure they are highlighted in green). Thus, we got vanish points in the space of the original image. Unfortunately, they cannot be depicted on it, because they lie far beyond it. Knowing the positions of these points, we drew virtual lines intersecting at them - we look again at the first picture, they are highlighted in green there.
Now we can straighten the original image by correcting the vertical perspective on it. Let's build virtual quadrangles of pages on the original image. We need to somehow set the coordinates of the four corners of the document, with which we can build a projective transformation. It is worth noting that such a construction is not unique, based on the nature of the observed things, we have chosen the following option: we believe that our quadrangles are trapezoidal, their bases are perpendicular to the root line, which is one of the sides, and the other side passes through the vanish point and the middle of the side of the image. So, on the one hand, we don’t cut too much from the picture, and on the other hand, we don’t make our quadrilaterals too big. Here, for example, another picture, but the principle does not change from this:
Of course, you can put the base of the trapezoid higher or lower, move the outer sides outward or inward and get other projective transformations at the same time, but at this stage it is only important for us that the spine becomes vertical and the lines are the same length. We apply the obtained projective transformations independently for each of the pages, we get: The
vertical perspective can be considered corrected. We turn now to the extension of the curved lines.
We select the oblique "fragments" of words in the image (and for this, the picture is binarized, connected components are highlighted on it, a graph is constructed that describes their relative position, the words are preassembled). The color shows the slope of the fragment: if <0 - green, if> 0 - red, equal to 0 (rounded to 1 degree) - blue.
Here, by “fragment” we mean “glued into a word” connected components. It may correspond to the whole word, or some fragment of the word, this is only the result of a preliminary analysis, not claiming to be true. You can see that not all words stood out, but this will be enough to build a page model.
We use the following page model:
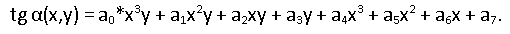
What does this formula tell us? The tangent of the local angle of inclination of the rows is a polynomial of degree 3 horizontally and degree 1 vertically (hereinafter we use the usual Cartesian coordinates on the plane). In fact, if we assume that the page distortions in space are cylindrical (the bending radius of the sheet depends only on the x coordinate), then the dependence of the vertical tilt angle when projected onto the image plane will be linear. In the horizontal direction, we believe that a 3rd degree polynomial will describe the varying angle of inclination with sufficient accuracy. Of course, we tried polynomials of smaller and greater degrees. In general, the choice of model is somewhat arbitrary, it is important that it describes the observed values of the angles well enough. And where will we get them from? Of those same oblique fragments of words.
We use the familiar MNCs to find the vector of parameters
. Next, we filter out emissions, because we could have mistakenly selected something else instead of a fragment of a word (we had a rough, preliminary analysis).
Here
is the angle calculated by the model at a point with the coordinates of the center of the i- th fragment,
- the value of the slope of the fragment (source data), the values of the angles are given in radians. If, as a result of filtering, we still have a sufficient number of fragments described by the model with a given error, we can refine it by applying OLS to the remaining data. Thus we get a preliminary page model. It describes the curved lines quite well in those parts of the image where we had allocated a sufficient number of word fragments, however, the solution is inaccurate in the root area. If we use it to straighten lines, this area will be distorted.
Let's try to “trace” the lines to the end using our model. The centers of the word fragments will serve as “seeds” for the tracking algorithm.
Let's prepare an image for tracing curved lines:
- binarization,
- horizontal closure (assembling lines),
- horizontal opening (getting rid of uppercase, extension elements),
- Gaussian smoothing (blurring the lines a little vertically).
We perform closing and opening with a window of width R = w / 100 , where w is the image width. We perform smoothing with σ = h / 400 , where h is the image height.
We trace the lines starting from the center of each fragment of the word in both directions.
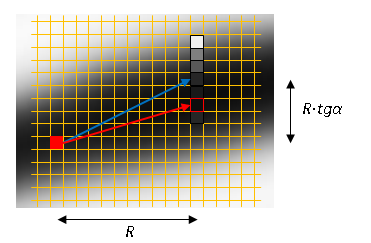
Each time we shift to a fixed horizontal pitch R and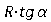
vertically. The angle value is determined by the model. We do a search for a local maximum in a vertical column with a height of ± 3 pixels. We continue the process from the specified position. The stopping criterion is the absence of a local maximum or the maximum value does not exceed the noise threshold (T = 30) .
As a result of tracking, we get much more data - segments with an updated value of the angle of inclination. We refine our model using this data.
Using the map of angles obtained from the model, we construct a map of local displacements. We take into account the angle of horizontal perspective at the current point:
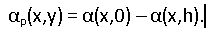
Multiply the offset at any point by
. This allows you to "stretch" the letters in the spine.
► ► ►
We get an image that can already be fed to the OCR input. To build a nice-looking picture, you still have to work. We would like to get something like this:
How to do it (of course, automatically), we offer readers to reflect. In conclusion, we note that this algorithm has already found application in the mobile application ABBYY FineScanner , which is now able to process photos of book spreads.
So, we believe that we have already found the spine line in the photograph, we will use this knowledge to determine the vanishing points for the reversal pages ( vanishing point) Vanish points are points of convergence of parallel lines in a perspective projection of a book onto the image plane. Both of them should be located on the continuation of this line, but for each of the pages the position of the point may be different. This is shown schematically in the following illustration (in fact, this is a log for debugging). The spine line is highlighted in red, the lines intersecting at the vanish points are green.
As a rule, the vanish points of two pages are not far from each other, but the above example shows that this does not always happen: for the left page of this spread, the green lines converge very weakly and the vanish point lies far below, and for the right - at the top, relatively close to the edge of the image.
How can I find these lines in the image? Again, the Hough transform (Hough transform ), only the image we need to prepare for this accordingly. We will try to highlight the boundaries of text blocks in the image in the simplest possible way. To do this, we perform the following simple steps:
1) Binarization;
2) Normalization of the image in size, for example, up to 800 pixels on the long side;
3) Morphological building (dilation, r = 6);
4) Morphological gradient (r = 1).
If we apply the fast Hough transform to the resulting image, we get:
Several local maxima corresponding to the borders of pages and text blocks are clearly distinguishable on it. The root line divides these sets into two (let us call them “left” and “right”, respectively), and each of them is well described by a line in Hough space. As you know, lines in Hough's space correspond to points in the image space. These are the desired vanish points.
To search for lines in Hough space, it is proposed to first select local maxima using the non-maximum suppression algorithm. We discard all maxima weaker than 0.2 of the largest. In principle, noise can be filtered in a different way, it is important to leave only points corresponding to fairly long contours in the gradient image. The group of maxima from the neighborhood of the point corresponding to the root line (it is highlighted in red at the beginning of the article), we average and add the center of this cluster to the “left” and “right” sets of points with increased weight. We use the least squares method ( OLS) to search for lines describing our sets of points (in the figure they are highlighted in green). Thus, we got vanish points in the space of the original image. Unfortunately, they cannot be depicted on it, because they lie far beyond it. Knowing the positions of these points, we drew virtual lines intersecting at them - we look again at the first picture, they are highlighted in green there.
Now we can straighten the original image by correcting the vertical perspective on it. Let's build virtual quadrangles of pages on the original image. We need to somehow set the coordinates of the four corners of the document, with which we can build a projective transformation. It is worth noting that such a construction is not unique, based on the nature of the observed things, we have chosen the following option: we believe that our quadrangles are trapezoidal, their bases are perpendicular to the root line, which is one of the sides, and the other side passes through the vanish point and the middle of the side of the image. So, on the one hand, we don’t cut too much from the picture, and on the other hand, we don’t make our quadrilaterals too big. Here, for example, another picture, but the principle does not change from this:
Of course, you can put the base of the trapezoid higher or lower, move the outer sides outward or inward and get other projective transformations at the same time, but at this stage it is only important for us that the spine becomes vertical and the lines are the same length. We apply the obtained projective transformations independently for each of the pages, we get: The
vertical perspective can be considered corrected. We turn now to the extension of the curved lines.
We select the oblique "fragments" of words in the image (and for this, the picture is binarized, connected components are highlighted on it, a graph is constructed that describes their relative position, the words are preassembled). The color shows the slope of the fragment: if <0 - green, if> 0 - red, equal to 0 (rounded to 1 degree) - blue.
Here, by “fragment” we mean “glued into a word” connected components. It may correspond to the whole word, or some fragment of the word, this is only the result of a preliminary analysis, not claiming to be true. You can see that not all words stood out, but this will be enough to build a page model.
We use the following page model:
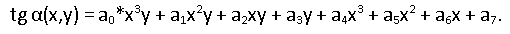
What does this formula tell us? The tangent of the local angle of inclination of the rows is a polynomial of degree 3 horizontally and degree 1 vertically (hereinafter we use the usual Cartesian coordinates on the plane). In fact, if we assume that the page distortions in space are cylindrical (the bending radius of the sheet depends only on the x coordinate), then the dependence of the vertical tilt angle when projected onto the image plane will be linear. In the horizontal direction, we believe that a 3rd degree polynomial will describe the varying angle of inclination with sufficient accuracy. Of course, we tried polynomials of smaller and greater degrees. In general, the choice of model is somewhat arbitrary, it is important that it describes the observed values of the angles well enough. And where will we get them from? Of those same oblique fragments of words.
We use the familiar MNCs to find the vector of parameters
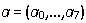. Next, we filter out emissions, because we could have mistakenly selected something else instead of a fragment of a word (we had a rough, preliminary analysis). Here
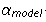is the angle calculated by the model at a point with the coordinates of the center of the i- th fragment,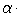- the value of the slope of the fragment (source data), the values of the angles are given in radians. If, as a result of filtering, we still have a sufficient number of fragments described by the model with a given error, we can refine it by applying OLS to the remaining data. Thus we get a preliminary page model. It describes the curved lines quite well in those parts of the image where we had allocated a sufficient number of word fragments, however, the solution is inaccurate in the root area. If we use it to straighten lines, this area will be distorted. Let's try to “trace” the lines to the end using our model. The centers of the word fragments will serve as “seeds” for the tracking algorithm.
Let's prepare an image for tracing curved lines:
- binarization,
- horizontal closure (assembling lines),
- horizontal opening (getting rid of uppercase, extension elements),
- Gaussian smoothing (blurring the lines a little vertically).
We perform closing and opening with a window of width R = w / 100 , where w is the image width. We perform smoothing with σ = h / 400 , where h is the image height.
We trace the lines starting from the center of each fragment of the word in both directions.
Each time we shift to a fixed horizontal pitch R and
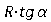vertically. The angle value is determined by the model. We do a search for a local maximum in a vertical column with a height of ± 3 pixels. We continue the process from the specified position. The stopping criterion is the absence of a local maximum or the maximum value does not exceed the noise threshold (T = 30) . As a result of tracking, we get much more data - segments with an updated value of the angle of inclination. We refine our model using this data.
Using the map of angles obtained from the model, we construct a map of local displacements. We take into account the angle of horizontal perspective at the current point:
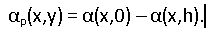
Multiply the offset at any point by
. This allows you to "stretch" the letters in the spine. ► ► ►We get an image that can already be fed to the OCR input. To build a nice-looking picture, you still have to work. We would like to get something like this:
How to do it (of course, automatically), we offer readers to reflect. In conclusion, we note that this algorithm has already found application in the mobile application ABBYY FineScanner , which is now able to process photos of book spreads.