Embarrassed scientists admit that they still do not know the exact value of the gravitational interaction.
- Transfer

According to legend, the first experiment, which showed that all objects fall at the same speed, regardless of mass, was carried out by Galileo Galilei, standing on top of the Leaning Tower. Any two objects thrown down in the gravitational field, in the absence of air resistance (or neglecting it) will accelerate equally. Later this rule was briefly written down by Newton after he had studied this issue.
When we first started formulating the laws of physics, we did it empirically: through experiments. Throw the ball from the tower, as Galileo may have done, and you will be able to measure how much he flies and in what time it will fall. Release the pendulum, and you can find the relationship between its length and the amount of time for one period. Having done this with different distances, lengths and time intervals, you will begin to notice the system: the height of the fall of the object is proportional to the square of time, the period of the pendulum is proportional to the square root of its length.
But in order to turn proportions into equations, you need to pick one constant.
The orbits of the planets of the inner solar system are not perfectly round, but are close to circles. Mercury and Mars further deviate from the ideal, demonstrating the ellipticity of the orbits. In the middle of the XIX century, scientists began to notice the deviations of Mercury from the predictions of Newtonian gravity, which only the General Theory of Relativity in the XX century could explain. The same law of gravity, and the same constant, describe the effects of gravity on all scales, from Earth to space.
In these examples, and in many others, the role of the proportionality constant is G, the gravitational constant. The moon moves around the Earth, the planets - around the Sun, light is distorted by gravitational lensing, comets lose energy, running away from the Solar System - and all this happens in proportion to G. Even before Newton, in the 1640s and 1650s, Italian scientists Francesco Grimaldi and Giovanni Richcioli performed the first calculations of the gravitational constant, which means that it became the first of all certain fundamental constants, even ahead of the definition of the speed of light in 1676, performed by Ole Römer .

Newton's law of the world was replaced by Einstein's General Theory of Relativity. It was based on instantaneous range and was extremely straightforward. The magnitude of the gravitational constant G from this equation is still very poorly known.
If you take two masses in the universe and place them close to each other, they will attract. According to Newton's laws, valid for all masses, except for extremely large, and for all small distances, the strength of the force is associated with both masses, separating them by distance and the gravitational constant G. For several centuries we have refined our measurements of many fundamental constants to incredible accuracy. The speed of light c is known for sure: 299,792,458 m / s. Planck's constant управля, which controls quantum interactions, has a value of 1.05457180 × 10 -34 J * s, with an error of ± 0.000000013 × 10 -34 J * s.
But G comes out completely different.

Whether we use the description of gravity from Newton or Einstein, the magnitude of the force is determined, in particular, by the magnitude of the gravitational constant G, whose value must be measured experimentally, and cannot be inferred from the others.
In the 1930s, 6.67 × 10 -11 N * m 2 / kg 2 was obtained for the G value , in the 1940s it was updated to 6.673 × 10 -11 N * m 2 / kg 2 , and both measurements were made by Paul Hale . As might be expected, over time, the values were constantly improving, and the margin of error dropped from 0.1% to 0.04%, and reached 0.012% in the late 1990s thanks to the work of Barry Taylor from NIST.
If you look at the old copy of the bookletdata on particles, in which the values of the fundamental constants were given, then there you can find the value of G , equal to 6.67259 × 10 -11 N * m 2 / kg 2 , with an error of only 0.00085 × 10 -11 N * m 2 / kg 2 .
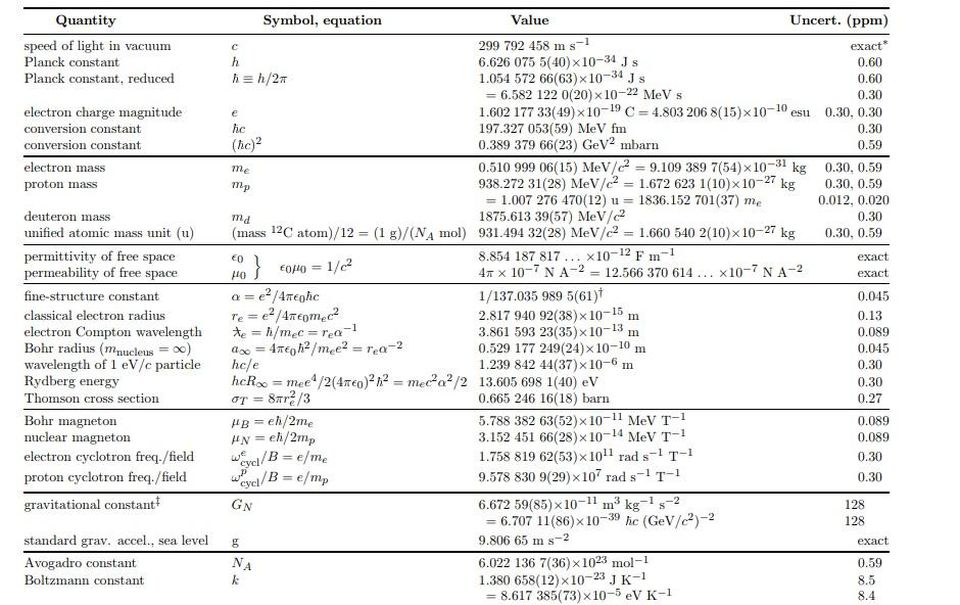
The values of the fundamental constants for 1998
And then something funny happened.
Later that year, the experiments found a value that was too high for the specified value: 6.674 × 10 -11 N * m 2 / kg 2. Different teams that used different methods received G values that did not coincide with each other by 0.15%, which is more than ten times higher than the error reported earlier.
How did this happen?

The initial experiment on the exact measurement of G, developed and published by Henry Cavendish , is based on the principle of torsional weights , spinning depending on the gravitational attraction of a nearby mass of well-known magnitude.
The first accurate measurement of the gravitational constant, not dependent on other unknowns (for example, on the mass of the Sun or the mass of the Earth) took place only in the experiment of Henry Cavendish at the end of the XVIII century. Cavendish developed an experiment known as torsion scales, in which a small dumbbell was suspended and perfectly balanced on a wire. Next to each of the masses at the end of the dumbbell were two larger masses gravitationally attracting small masses. The amount of rotation of the dumbbell at known distances and masses gave us the opportunity to measure G experimentally.
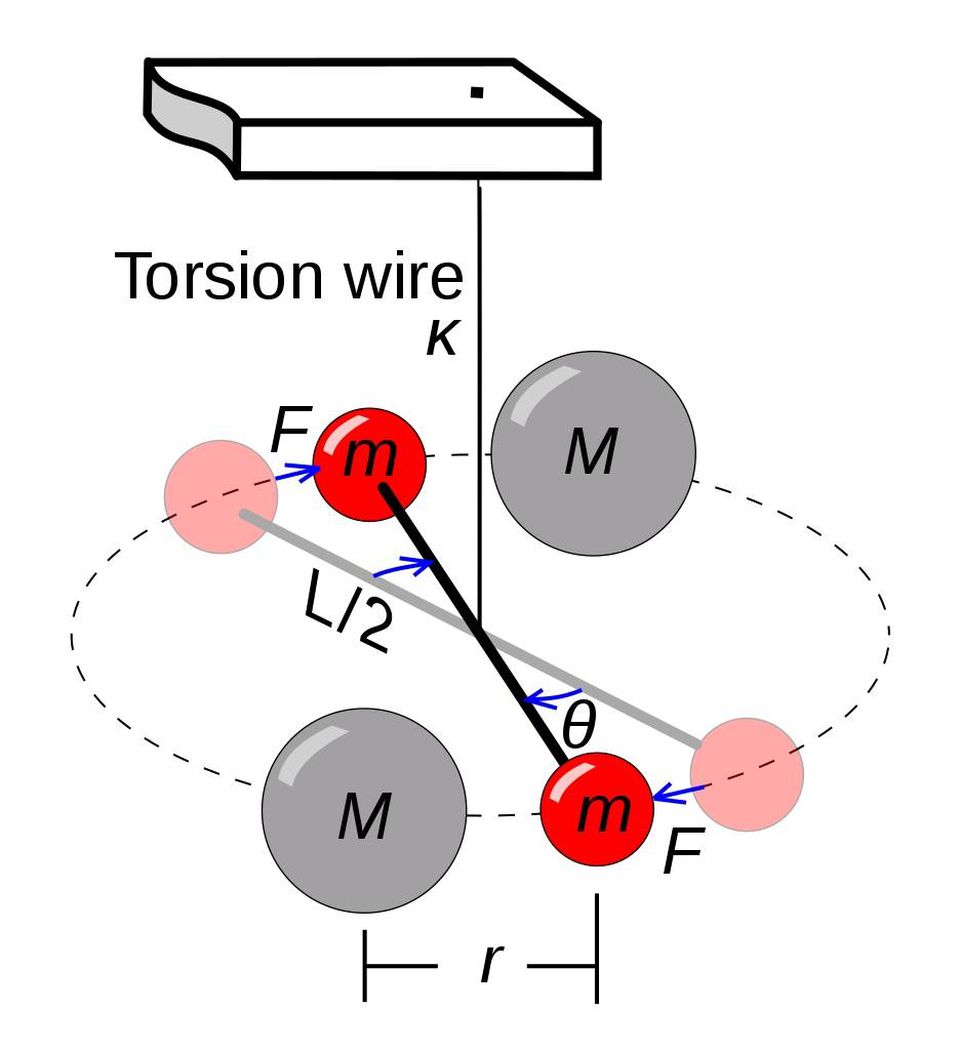
Despite many breakthroughs in physics over the past 200 years, the same principle used in the Cavendish experiment is used in experiments on measuring G. Up until today, no other measurement technique or experiment device has yielded better results.
There is a suspicion that one of the reasons for the discrepancies is the well-known psychological factor of confirmation bias . If all your colleagues get the result of the type 6.67259 × 10 -11 N * m 2 / kg 2 , it is reasonable to expect that you will get a result of the type 6.67224 × 10 -11 N * m 2 / kg 2 , or 6.67293 × 10 -11 N * m 2 / kg2 ; but if you get something like 6,67532 × 10 -11 N * m 2 / kg 2 , you decide that you did something wrong.
You will look for sources of error until you find it. You will repeat the experiment again and again until you get something reasonable: something that does not contradict the value of 6.67259 × 10 -11 N * m 2 / kg 2 .
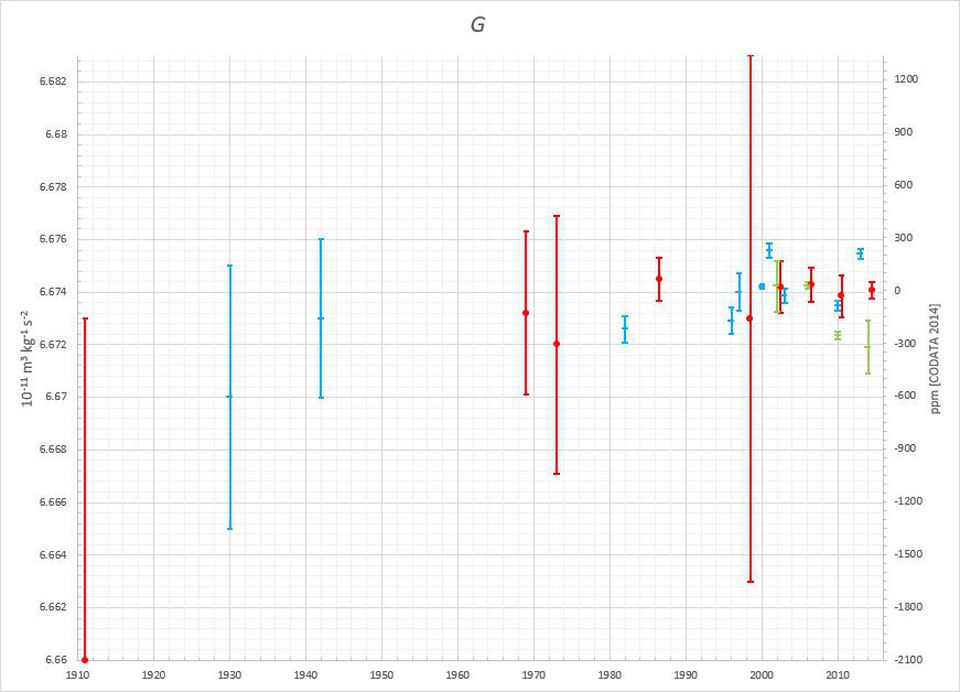
In 1997, the team of Bagley and Luther conducted an experiment with torsional weights, which gave a result of 6.674 × 10 -11 N * m 2 / kg 2 , which was taken seriously enough to cast doubt on the previous measurement error G
Therefore, such a shock was the event of 1998, when a very carefully working team got a result that differed by an incredible 0.15% from the previous ones, while the stated errors of previous measurements were ten times smaller than this. NIST, in response, rejected previous errors, and the resulting values were cut to four significant digits, and the error was increased.
Torsion scales and torsion pendulums, made under the influence of the original Cavendish experiment, continue to lead in G measurements, ahead of more modern atomic interferometry technologies. Only this August, the Chinese team announced the receipt of the most accurate G value from two independent measurements: 6.674184 × 10 -11 N * m 2 / kg 2 and 6.674484 × 10 -11N * m 2 / kg 2 with an error of 0,0011%.
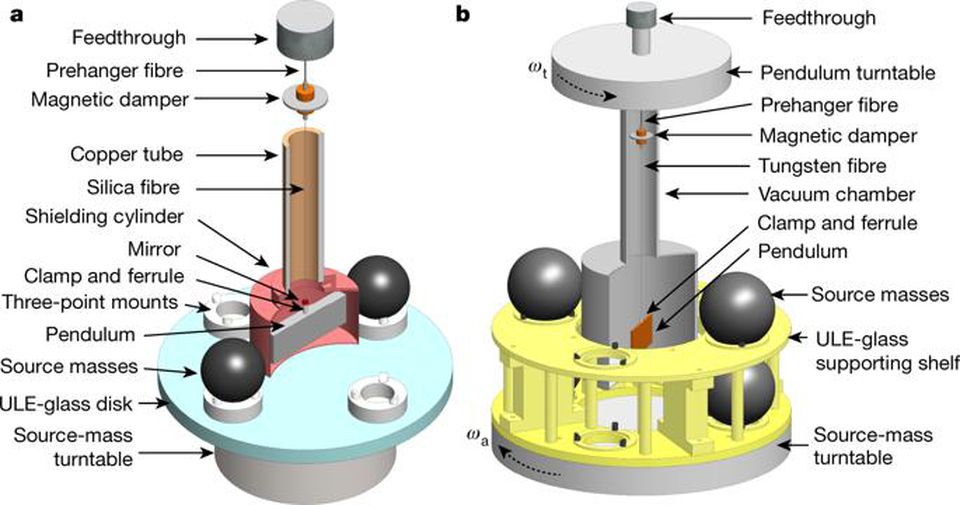
Two experimental setups, whose diagrams were published in August 2018 in the journal Nature, gave the most accurate (according to scientists) values for G
These values agree with each other within two standard deviations, but not consistent with other measurements made by other teams for 15 in recent years, varying from 6.6757 × 10 -11 N * m 2 / kg 2 to 6.6719 × 10 -11 N * m 2 / kg 2 . While other fundamental constants are known with an accuracy of 8 to 14 significant digits, when measuring G, errors are obtained thousands or billions of times large.
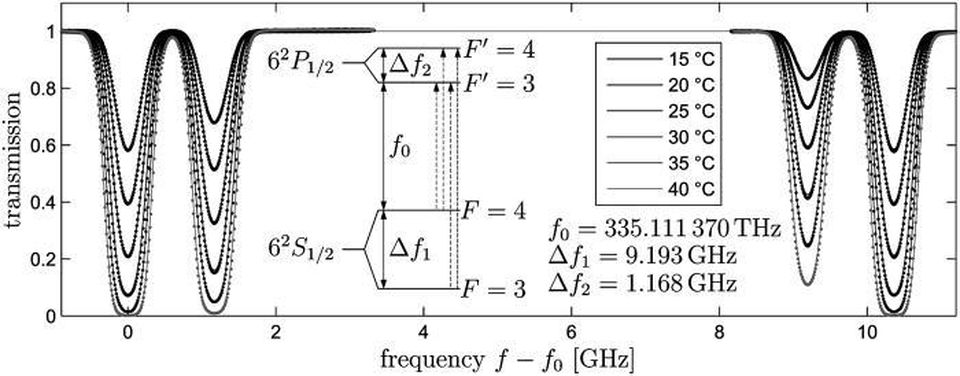
The atomic transition from the 6S orbital, Delta_f1, determines the meter, second, and speed of light. The accuracy of determining quantum constants is thousands of times greater than the accuracy of measuring G, the first of the measured constants.
The gravitational constant of the universe, G, was the first measured. However, 350 years after the first measurement, it is embarrassing to state how poorly known it is compared to all the others. We use this constant in a huge number of measurements and calculations, from gravitational waves to pulsars, which measure the expansion of the Universe. And yet our ability to determine it is based on small-scale experiments conducted on Earth. Our attempts to measure it are penetrated by tiny sources of uncertainty, from the density of materials to seismic vibrations. And as long as we fail to achieve more, wherever gravity is important, there will be an internal, unpleasantly large error. The year is 2018, and we still don’t know how great gravity really is.
More articles on the popular science topic can be found on the Golovanov.net website . Read: is plate tectonics necessary for life education on the planet; where does energy come from in dark energy; will not human activity lead to interstellar war; is there a healthy amount of alcohol; a series of articles on cosmology " Ask Ethan ".
Do not hesitate to support the project financially (bank cards, Yandex.Money, WebMoney, Bitcoins, whatever you like). Thanks to everyone who has already provided support!
