Good afternoon! We recently started a series of co-editing articles. In the first article, I talked about the problem of non-blocking editing and possible approaches to its implementation. Let me remind you that in the end, we chose Operation Transformation (OT) as the algorithm. A story about his client-server version was also announced, and today I will cover the details of his work. In addition, you will learn why cancellation in OT works differently and how it faces a harsh reality.

Further you will find many algorithms and diagrams. I think you will be interested.

Client server model

At the end of the previous article, I noted that difficulties in implementing the OT approach can be circumvented by a central server. Unlike the peer-to-peer algorithm, using the server allows you to enter a common order of operations for all - the order of operations on the server. Accordingly, at any time, the state of the document on the server is characterized by one number - a revision.



At the same time, the status of the document for any of the clients at any time can be represented as a certain revision on the server and a certain number of local operations that are still not consistent with the server.

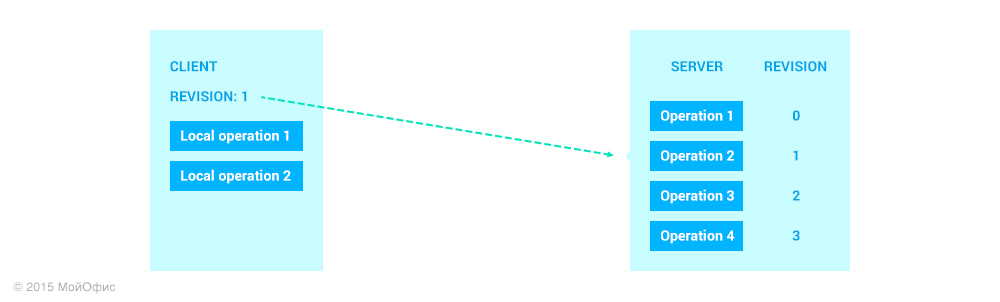
From server to client

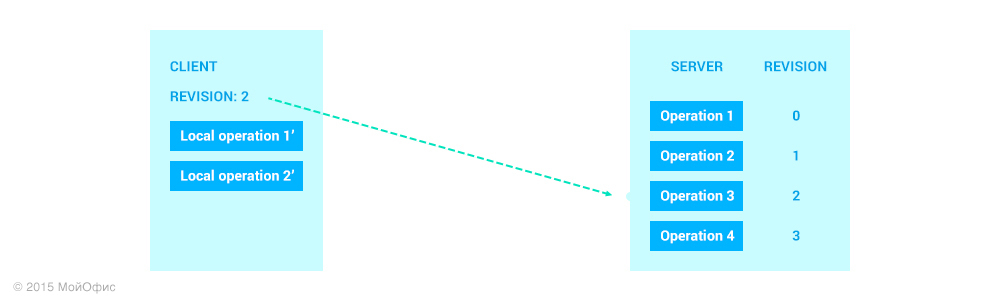
First, let's examine what happens when a client receives a new operation from the server. In this situation, everything is quite clear. It is assumed that all operations come to us in the order in which they are applied on the server. For this reason, we know the revision of the operation (revision on the client + 1).



Revision 1 is the latest overall document state for the server and this client. Recall the transformations that we examined in the previous article. With their help, we can "reduce" different ways of document modifications:



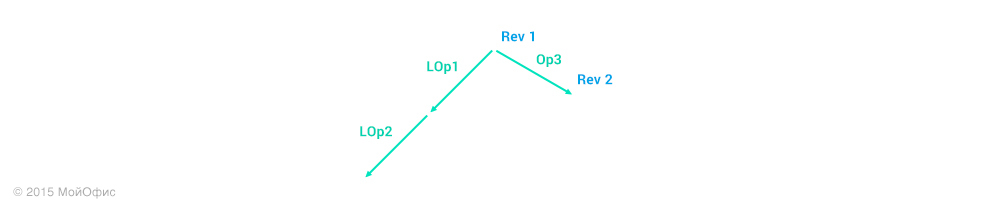
For clarity, in this and subsequent schemes I will use abbreviations, where Operation3 is Op3, Local operation 1 is LOp1, and so on. The right shoulder is the actions that are performed on the server. And the left one is on the client. We use the property of transformations, which is describeddiagram in the previous article:



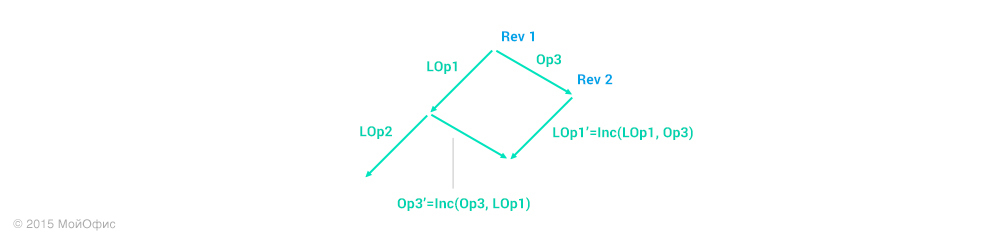
Repeat this action again:



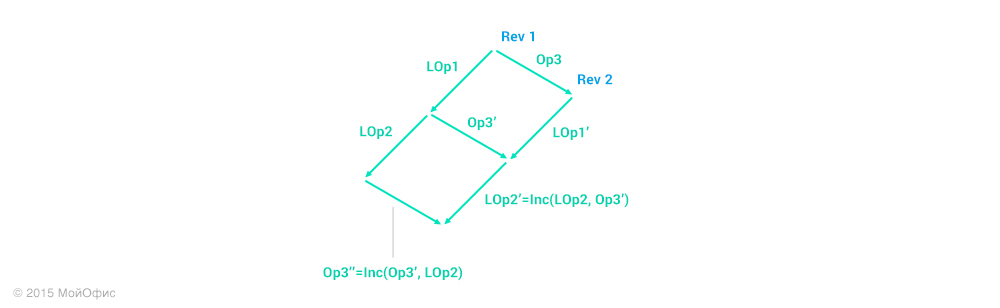
Further, we can act in two directions:

1. Apply the Op3 '' operation on the client, increment the revision and replace the local operations (LOp1, LOp2) with (LOp1 ', LOp2' ').
2. Roll back local operations and apply Op3, LOp1 ', LOp2' 'in sequence.

Whichever option we choose, as a result we get the client’s state like this:



Based on all the current considerations, everything looks like the results in both cases will be similar. And the first one is preferable for performance reasons. But we use the second method. I will explain how this is due in one of the following articles. In the meantime, take it as it is and continue.

From client to server

After we have considered sending data from the server to the client side, we will consider operations in the opposite direction. Let us return to the same state as in the example above:



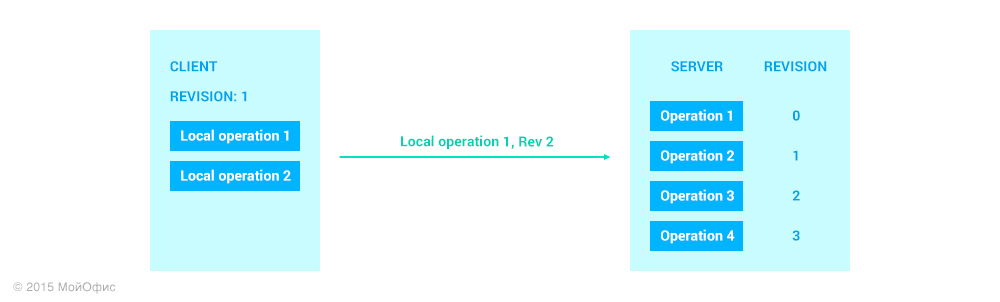
As you can see, together with the operation itself, the client sends a revision, which is currently common for the client and server. This eliminates the need for the server to use the history to restore the revision on which the sent operation was based. We apply the transformations again:



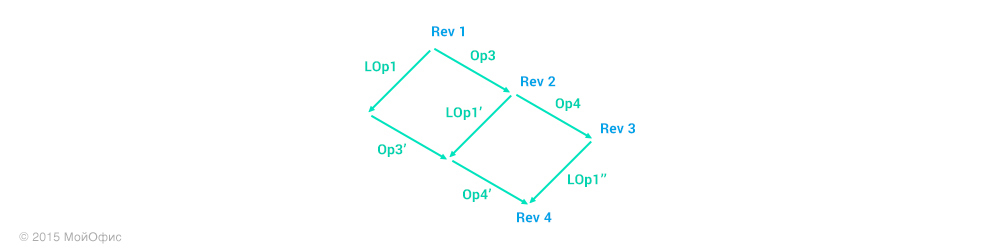
Here we can see that on the server it is necessary to apply the LOp1 ′ ′ operation and, accordingly, increase the revision. In addition, we must send the transformed operation to other clients who work with the document:



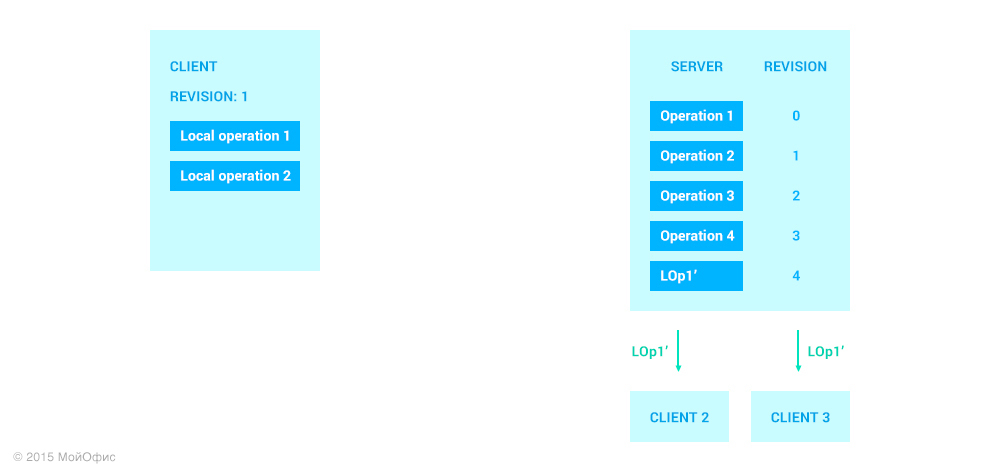
Please note that the status of the client has not changed. In order for him to be able to increase the audit, the server needs to send him a confirmation. It is understood that the communication channel preserves the message delivery order, which means that previously all operations with an audit less than that of LOp1 ′ will be sent to the client.

Moreover, the procedure when the client receives operations from the server ensures that after all the transformations the first of the local operations will have the value LOp1 ′, the same as the corresponding operation on the server.



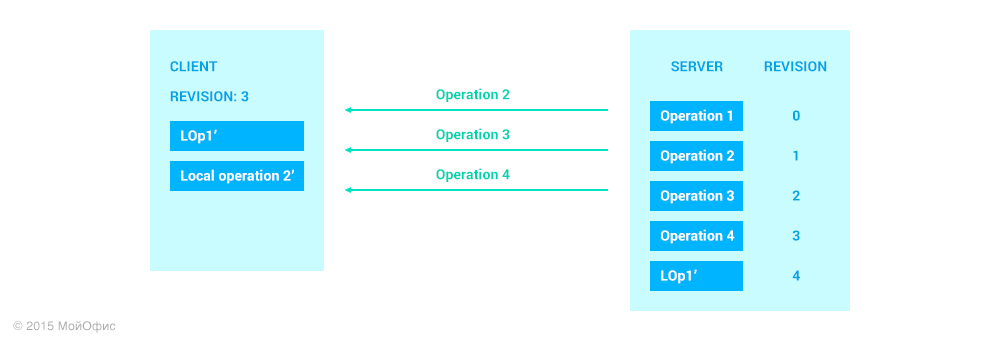
Upon receiving a confirmation message, the client increases the revision value. The value of this revision will be equal to the revision on the server that corresponds to the submitted operation. We also remove LOp1 ′ from the list of local operations of the client, since now it is also on the server.

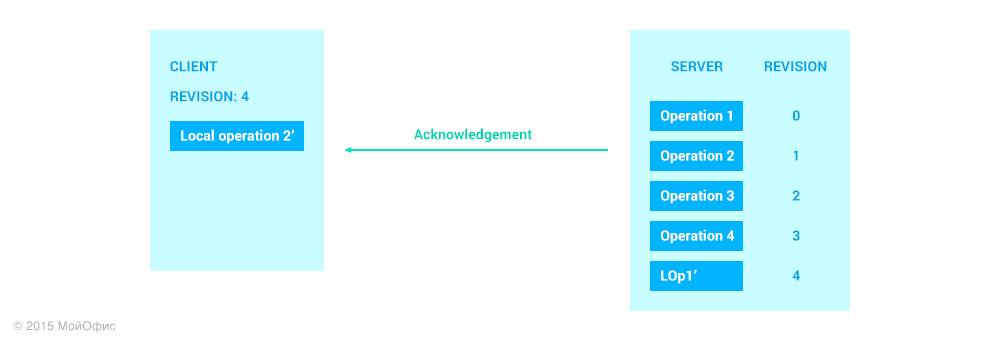
What happens next with Local Operation 2?

“What happens next with Local Operation 2?” You ask. Everything described above works for the first local operation. Let's see what will happen to the second. Imagine that as soon as the client added Local Operation 2, we immediately send it to the server. At the same time, it is quite possible that operations from other clients can “wedge” between these operations on the server:



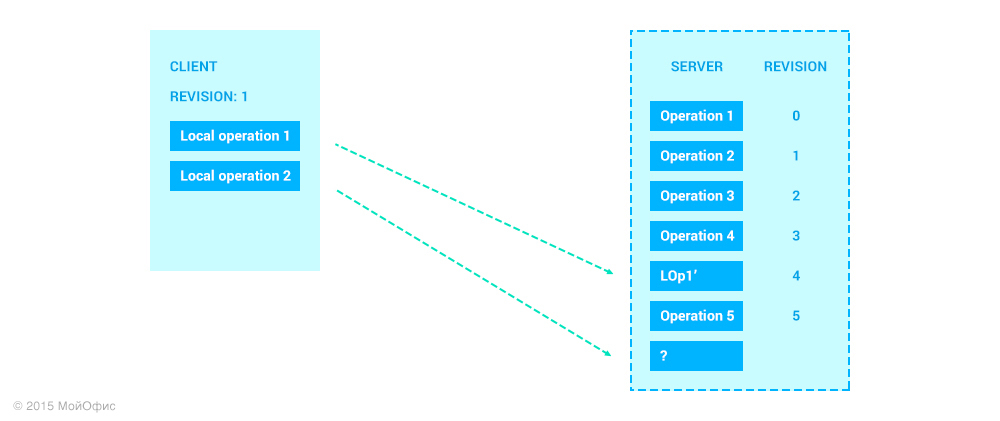
Now, to understand which operation to use on the server, it is necessary to solve the following problem:



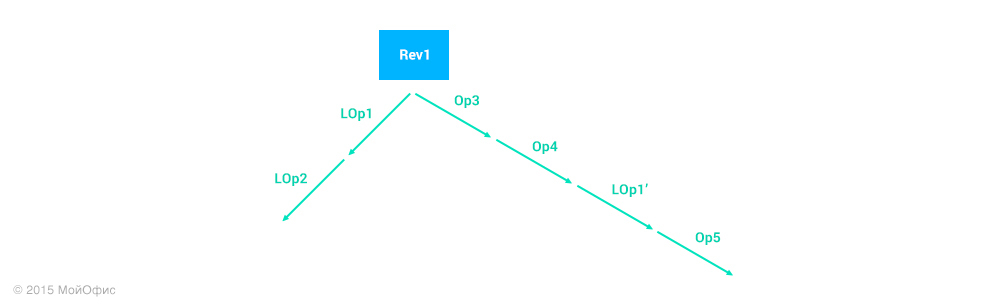
From the point of view of theory, nothing prevents us from doing this. It is enough to apply the transformations already mentioned many times to get the desired operation:



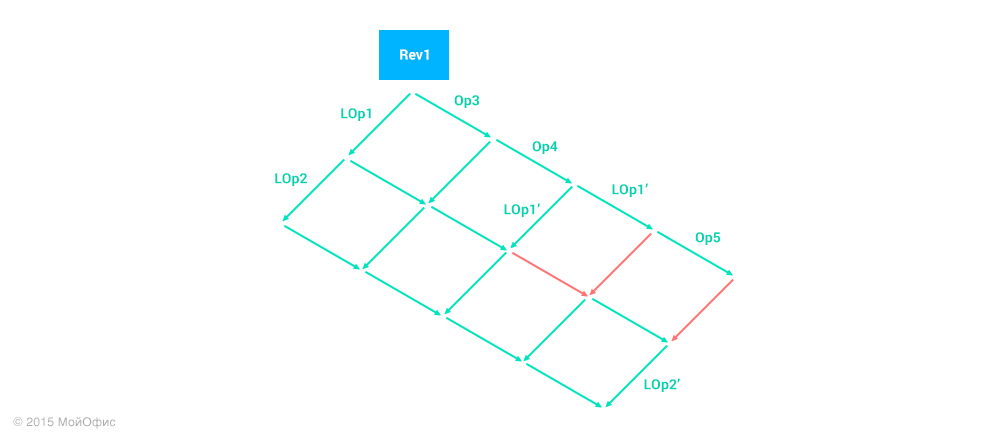
I did not designate all transformations, otherwise the circuit would turn out to be very bulky. But it is worth noting that the operations corresponding to the red arrows are empty (identical). This means that the operation LOp2 ′ is the change that we should apply to the server.

Let's look at these calculations from a practical point of view. To perform these transformations, the server needs to:

1. Know the revision with which the chart begins. This is not difficult, since together with the operation we can send a basic revision.
2. Have information about previous local operations of this client. In the above diagram, this is LOp1, but in the general case there can be any number of them. Moreover, it is important to have the state of these operations exactly at the time of sending LOp2, since it was shown above that when the operation comes from the server, local operations will be transformed, which can lead to their change.

The condition “Have information about previous local operations of the client” means that we must either send all previous local operations together with LOp2, or restore them using transformations on the server. You simply cannot use operations from this client in the history on the server, since they have already undergone transformations. In the first case, network traffic is greatly increased, and in the second, the load on the server increases.

The algorithm used by Google Docs and Wave uses a simple but effective solution that allows you to choose between two evils. The idea is to not send the next local operation until confirmation is received that the previous was successfully applied on the server. In our case, this means that LOp2 will only be sent after we receive a confirmation message from the server regarding acknowledgment of LOp1: We



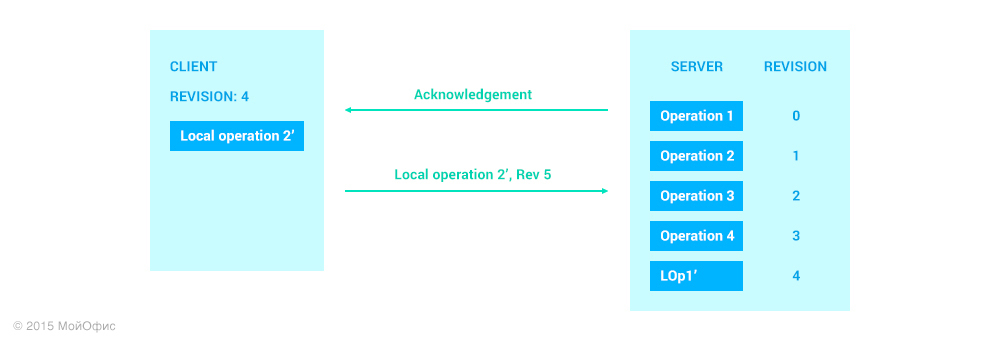
use the same approach.

Total

How these rules work “live” can be seen on the slides.

Cancel Edit (Undo)

The possibility of co-editing makes such a mundane function, like undoing a user action, very specific. Take a look at how this should look like on the part of the user.

Suppose we have two people who edit different parts of a document. One of them did not like the last change, and he presses the cancel button. If the system does as local text editors do - it rolls back the last change from the history of all edits, then this may well lead to the cancellation of another user's operation. In this case, both will be confused:

• The one who initiated the cancellation will not see the expected result.
• His colleague will suddenly have his text just deleted. Well, or the remote appears.

This means that it is appropriate to cancel not the last operation in time, but the last operation of the user who initiates the cancellation. In this case, the effect will be more expected and close to the usual one, which we can observe when editing local documents. Accordingly, each user has their own undo-redo stack.

However, in the history of client operations, the latter may be an operation from another user that he received from the server. Because of this, it becomes impossible to apply the approach for undo-redo, which is used when editing local documents: when canceled, the top one is taken from the stack and rolled back. In our case, we would have to somehow extract the operation from the "middle" of history and transform all the following:



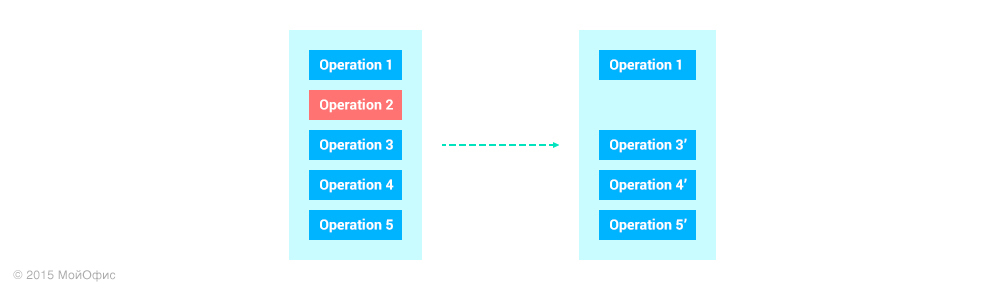
An important property in the algorithm we use is that operations that are already coordinated with the server do not change. And if this property is violated, then the algorithm will no longer work. So, such a principle of cancellation does not suit us.

We need to roll back an operation that has already plunged into the abyss of history (a stack of document operations). For this, we have one way left: to create a new operation, which will cancel the effect of the original. We assume that for each operation you can generate the opposite. It is important that the reverse operation can only be correctly applied to the state of the document that occurs immediately after the initial operation.



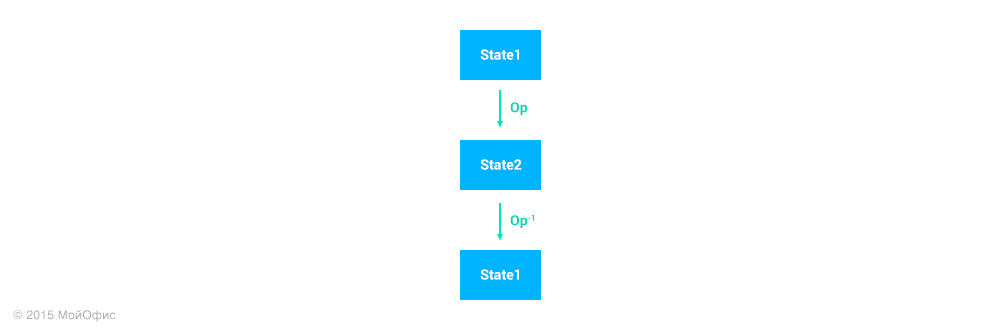
With the help of transformations, we can “transfer” the reverse operation to the current state of the document on the client, as we did earlier with the edits:



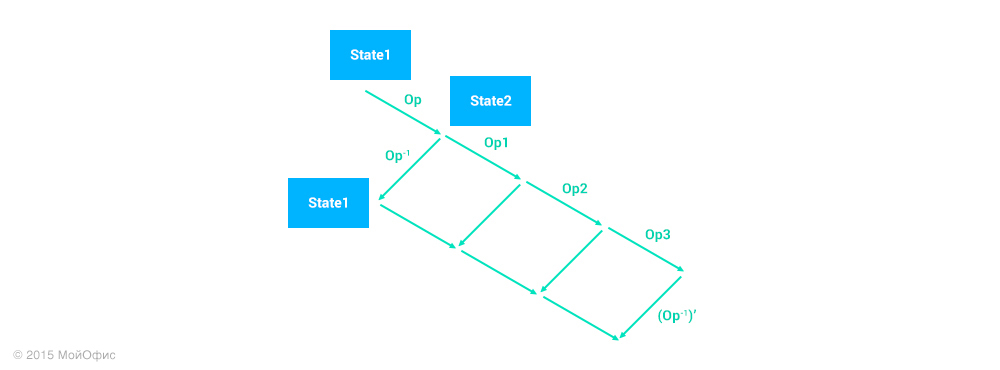
On the diagram (Op ^-1 ) ′, this is just the right operation. No more changes to the existing algorithm are required: the operation is applied locally and sent to the server like any other. Neither the server nor other clients can distinguish an undo operation from a regular one. Information that this was a cancellation operation is saved only by the user who created it, since it is necessary for redo to work correctly.

Practice

In theory, there is no difference between theory and practice.
But, in practice, there is.
Johannes Lambertus Adriana van de Snepscheut

At the moment, we already have an algorithm that allows for non-blocking simultaneous editing with the ability to cancel operations. At this stage, in most theoretical articles it is assumed that the task of constructing the algorithm is solved. An example of editing one line is used as a “test site”, where there are only two editing operations: insert and delete a character. Sometimes they give an example where a symbol has some property and, accordingly, a third operation appears to change its value. I don’t just mention the total number of operations, because we need to be able to transform any of the operations relative to any other, which means that for N operations, we need to implement N ² transformations. When operations are two or three, this is not a problem.

To date, the kernel interface of our product contains more than fifty functions for editing a document. If we present each of them as a separate operation, then we will have to implement and test more than 2500 transformations, which is simply physically impossible. In addition, we are constantly adding new functionality, so this number continues to grow.

A natural solution in this case is to abandon the one-to-one correspondence between user actions and operations. The set of operations should be minimal, but such that with the help of a sequence of operations it would be possible to describe any user action. Moreover, if we want to limit the number of operations as much as possible, the operations themselves must be universal. The fact is that, from the point of view of transformations, there is no difference between the operations of setting the font color or its size. Just as there is no difference between inserting a character or inserting a paragraph - all this is pasting into a one-dimensional collection. As a result, it turns out that there remain three fundamentally different operations: inserting an element, deleting and setting the property of an object.

Products like CoWord, represent the whole document in the form of a sequential list of different types of elements: letters, carriage translations, pictures, etc. And for such a document model, the proposed three operations are quite enough. But the problem is that this model does not allow to fully present an office document with styles, headers, footers and tables.

Document like a tree

Instead of a list, it is natural to imagine a document as a tree reflecting its hierarchical structure. To simplify, the document in this model looks like this:



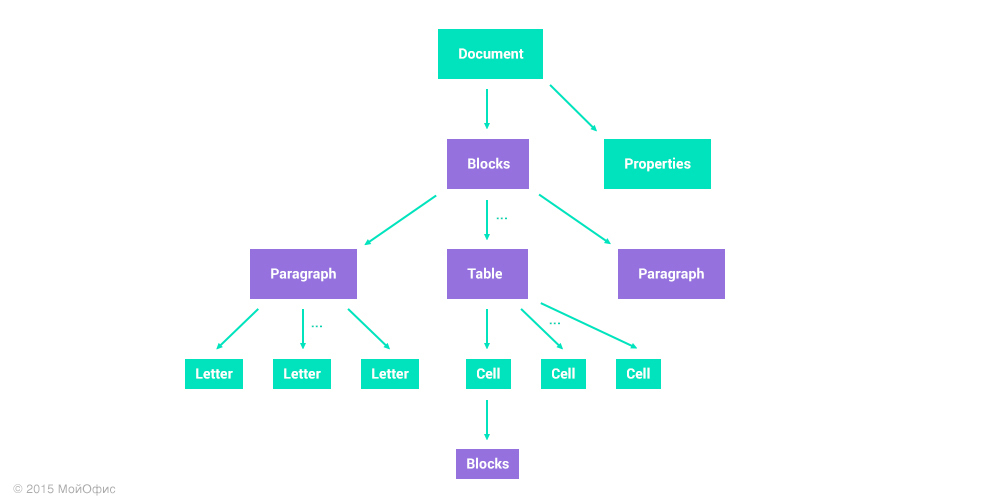
I deliberately reduced the number of types of elements in order to simplify the scheme, but the meaning remained. The document is presented in the form of a tree with two types of nodes:

1. Fixed structure nodes are marked in green. As an example, take the root element. Any document within this model will always have two child nodes: a list of blocks and a set of properties.
2. Collection nodes, which may contain a variable number of child nodes, are marked in purple. For example, blocks (paragraphs or tables) in a document may have a different number. Similarly with the letters in the paragraph and the rows and columns in the table.

Having such a document model, you can use the same three primitive operations: insert, delete, and set the property. At the same time, the node address in the document tree on which it is performed is added to each operation. For insert or delete operations, this must be the address of the collection; for setting the property, this is the address of the node from which we want to change this property.

Transformations of tree operations

Addresses of operations help us with transformations. Suppose we have two operations - (Operation1, address1) and (Operation2, address2). Let us determine how the relative position of the nodes over which they are held affects the value of Inc ((Operation1, address1), (Operation2, address2)). There can be four different cases:

1. Nodes match, address1 = address2.


.
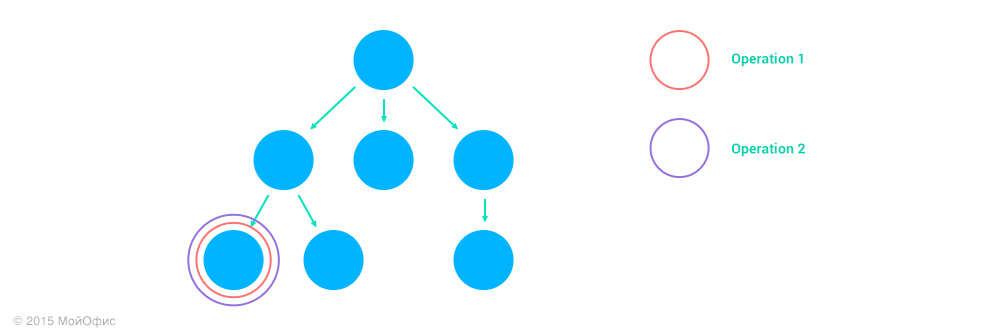
In this case, the transformation takes place as if the document we had was flat. The address remains the same:

Inc ((Operation1, address1), (Operation2, address2)) = (Inc (Operation1, Operation2), address1)

2. Operation2 acts on the ancestor of the node Operation1, address2 is the prefix address1.



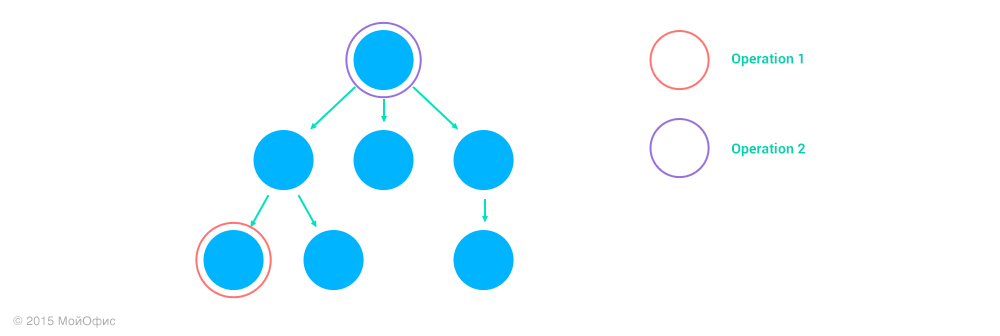
If Operation2 deletes the ancestor of the node Operation1, then as a result we get an empty operation. If it does not delete, then Operation1 itself will not change, but its address may change if Operation2 changes the collection. For example, if Operation1 is the insertion of a character in the second paragraph, and Operation2 is the deletion of the first paragraph, then as a result we get the insertion of the character with the same index, but in the first paragraph:

Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, Inc (address1, Operation2))

3. Operation1 acts on the ancestor of the node Operation2, address1 is the prefix address2.



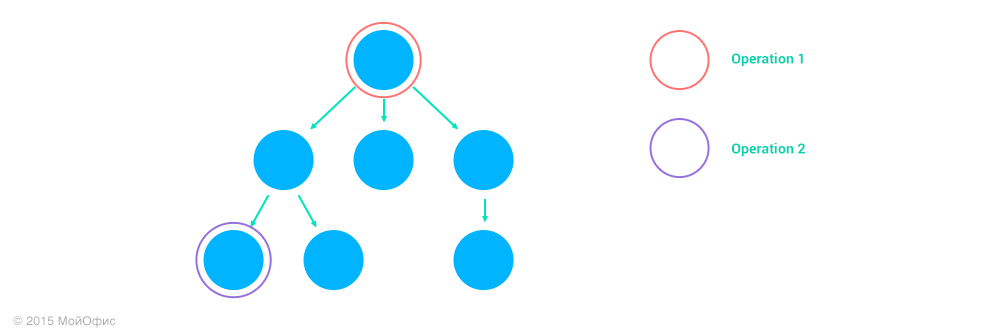
In this case, Operation2 does not affect Operation1:

Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, address1)

4. Operation1 and Operation2 operate on various nodes, none of which is the ancestor of the other.



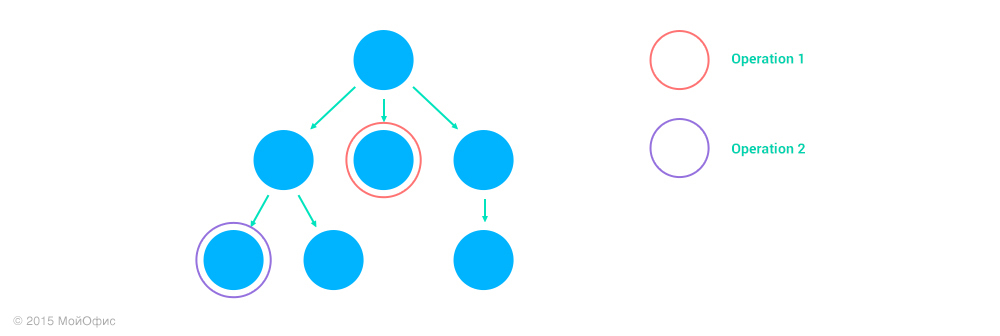
Here, too, the transformation is identical:

Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, address1)

These rules allow us to get the transformation for any pair of operations. In addition, operations on various parts of the document will not be transformed, which positively affects productivity.

Two-dimensional collections

Separately, it is worth mentioning the tables. I have met several publications where authors review OT over a hierarchical document. However, lists have always been used as collection nodes. When it came to tables, it was said that they can always be specified as a list of rows or columns, which in turn are a list of cells. This approach is fundamentally wrong, because it does not allow you to correctly mutually transform operations on rows and operations on columns. And now I will tell you why.

Imagine that we store a 2 by 2 table in the form of a list of rows:



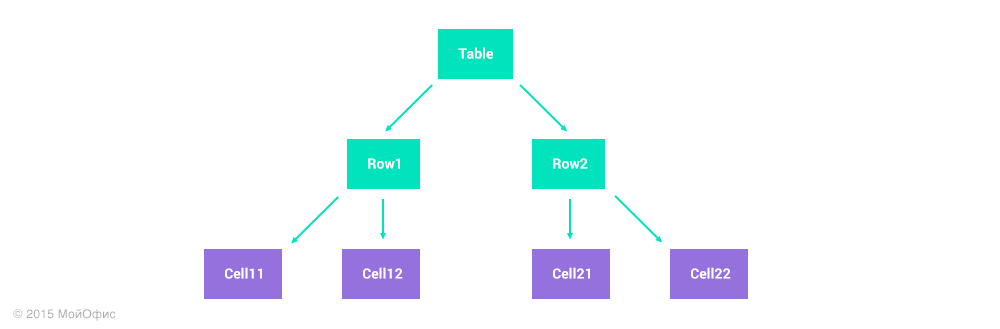
Suppose one user inserts a row at the end of the table, and the second deletes the right column in parallel. For the first user, his action is described by a single operation: insert (Table, 3, {Cell31, Cell32}). The second will need two operations: remove (Row1, 2), remove (Row2, 2). If we apply all the transformation rules described above, then as a result we get this state of the table:



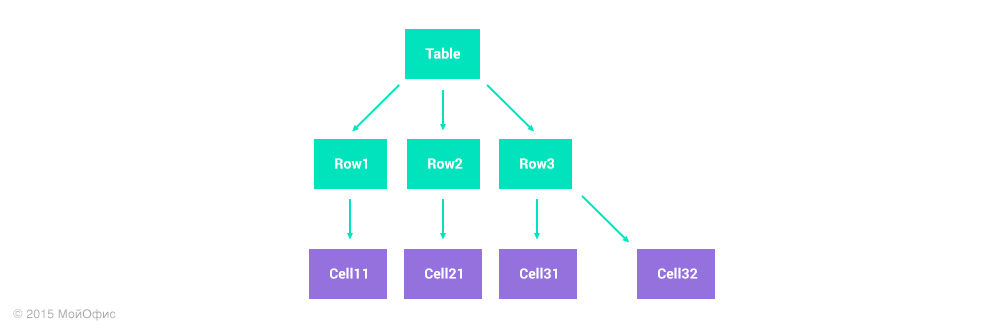
Either we admit not quite rectangular tables, or we find a different approach. We chose the second option. More precisely, they presented the tables as a separate, two-dimensional type of collection. In contrast to the list, operations on them can be not two, but four: insertion and deletion of columns and similar for rows. And the address of the child element - the cell - is set not by a single numerical index, but by a pair. This approach allows you to correctly represent and transform operations on rows and columns and to prevent situations with incorrect table structure.

Conclusion

On this I would like to exhale and write that this is all. For OT, the phrase “the devil in the details” is incredibly accurate, since real little things turn into the need to solve fundamental problems and complicate the algorithm. Therefore, in the real algorithm of operations on lists, we have not two, but four. And one of them is never executed. And the operation can change not only during the transformations, but also at the time of execution.

It is simply no longer possible to cover all the nuances in this article, and we will leave them to continue, and we will finish this second article.

See you!