About really BIG numbers (part 1)

The idea to write popularly about large numbers came when I read a recent article that talked about giant numbers that have at least some physical meaning. And it ends with a mention of the Graham number. That number, which will be the starting point of today's article. To imagine the scale of the disaster, I strongly recommend that you read this article in advance , which explains the Graham number on ^_TM’s fingers , where the author very colorfully and consistently talks about the boundaries of perception into which we pinch ourselves when talking about large numbers.To begin with, in order to prevent possible comments in the style of “but what for it is necessary, it still doesn’t have any practical meaning” - the answer is In general, as IngvarrT said in a discussion of an article about giant numbers, all of the rest of the text boils down to the phrase “Think it over, mathematicians came up with it.”

To begin with, it is necessary to clarify that when we talk about large numbers (not even BIG, but just big), then as a rule we do not mean the sequence of digits that make up this number, but the method (or method) by which this number is obtained. Of course, we can write sextillion as 1,000,000,000,000,000,000,000, but it’s still more common to see 10 ²¹. In this case, the method of describing the number is an exponentiation operation (which looks like writing a number by the superscript on the right). The use of such methods makes it possible to reduce the notation of a number, leaving only the method of its formation (which, of course, is quite sufficient for performing mathematical operations on it). So we logically came to the conclusion that all conversations in LARGE numbers come down to finding the most compact record of the largest possible number. So, "these mathematicians came up with the same thing."

We all know three basic arithmetic operations: addition ( a + b ), multiplication ( a × b ), exponentiation ( a ^b ). Ever thought that all these operations sequentially flow from one another? And if so:







Generally, these operations are called hyperoperators. For addition, multiplication and exponentiation - 1st, 2nd and 3rd order, respectively. The continuation of this series to higher orders suggests itself: sequential exponentiation is called a 4-order hyperoperator (tetration):



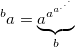
But for higher-order hyperoperators, this notation will not work - power towers will be too bulky and confusing. Therefore, to designate large numbers, other notation systems are used.

One of the most common is the arrow notation of Donald Knuthproposed in 1976. The principle of writing numbers follows from a sequence of hyperoperators and, by and large, is an explicit indication of the order of the hyperoperator. The usual exponentiation (hyperoperator of 3 orders) is indicated by one arrow: a ↑ b , tetration - by two arrows a ↑↑ b and so on. Here's how the tetration is calculated:



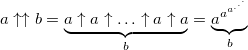
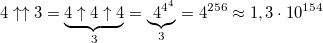
Changing just one digit, we get a giant increase in the value of the number:

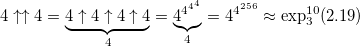- in this number, more than 10 ¹⁵³ digits.

Adding another arrow, we get a 4-order hyperoperator - pentation:




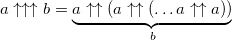
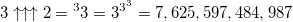
Changing one digit here leads to such a large increase in the value that epithets can not be selected:
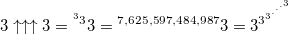- the height of the power tower is 7,625,597,484,987 elements ...
(this number is called tritri , and it is still useful to us)
In order not to draw a lot of arrows, we use the abbreviated notation: a ↑ ^_n b to denote a ↑↑ ... ↑ b with n arrows.

Here you need to be extremely careful in estimating the growth rate of the function as the order of the hyperoperator increases (you’ll obviously make a mistake to the lower side) - if you do not pentate three and hex three (well, just increase n by one), then we should 3 times pent three, that is, 3 Pentify in three 7,625,597,484,987 times ... (but do not relax, all this is only the beginning, the very beginning).
By the way, have you already guessed what is the weakest point of Knuth's arrow notation? Yes it isn is the number of arrows. But what if it is so large that the usual number is no longer able to transmit it? A short digression: if three, pentinated in two, lends itself to at least some understanding, then already three, pentinated in three, cannot be imagined or realized. Without even stuttering about the following orders of hyperoperators. This is an area of ​​pure, uncomplicated abstract math and, damn it, it's fucking awesome!

The solution to Knuth’s notation is Conway’s chains . They are used when even Knut's arrow notation becomes too cumbersome to write a number. Remember the Graham number mentioned at the beginning? Marking it with Knut's arrows is simply impossible. The definition of the chain and its relationship with the Knut arrows:



Everything seems to be the same. But the problem of the “number of arrows” in Conway’s chains is solved easily and elegantly: by adding one more arrow. And each arrow draws the entire previous chain to itself. Let's try to figure out an example: take the tetration 3 → 3 → 2 (what it is: take the first two numbers and perform the operation of raising to a power three times), add on the right → 2.
3 → 3 → 2 → 2 = 3 → 3 → (3 → 3 → 1 → 2) → 1 = 3 → 3 → (3 → 3) = 3 → 3 → 27
Adding just one arrow, we immediately went to the 27th order hyperoperator. And the Graham number, which cannot be represented in the arrow notation of Knuth, is written in very concise chains by Conway chains: 3 → 3 → 64 → 2. But you can continue to add arrows and move on to increasingly unimaginable orders of numbers.

Ha! But is it right to draw so many arrows? Yes, and numbers are growing too slowly ... In general, Jonathan Bowers introduced massive notation , which in its most expanded form is called BEAF (Bowers Exploding Array Function, Bowers' explosive massive feature, pun with English beaf - beef. It should be noted that Bowers, even in his scientific works, has a special sense of humor). Writing it is very simple and resembles the notations already considered: 3 ↑↑↑ 3 = 3 → 3 → 3 = {3,3,3}. Another massive notation system is also used when the last element denoting the order of the hyperoperator is transferred to the middle of the record, i.e. {3,3,2} = 3 {2} 3 (the logic is this - we take two numbers at the edges and do with them what is indicated in the middle).
At this stage, there are no differences in massive notation from Conway chains. But adding the fourth element of the array has a completely different meaning, namely, the number of brackets: {3,3,3} = {3,3,3,1}, {3,3,3,2} = {{3,3, 3}}.
{a, b, 1,2} = a {{1}} b = a {a {a .... a {a {a} a} a ... a} a} a, where b is the number of a, diverging from the center.

For clarity, let's see what happens when an element inside the central brackets changes “by one”:
{3,3,1,2} = 3 {{1}} 3 = 3 {3 {3} 3} 3 = {3, 3 , {3, 3, 3}} = {3, 3, tritree}
{3,3,2,2} = 3 {{2}} 3 = 3 {{1}} 3 {{1}} 3 = { 3, {3, 3, tritri}, 1, 2} = 3 {3 {3 ... 3 {3 {3} 3} 3 ... 3} 3} 3, where the number of triples diverging from the center to the edges is {3 , 3, tritree}.

In comparison with Conway’s chains, the explosive growth of the number occurs a step earlier - if Conway’s only the fourth number turns all the previous operations onto itself, then Bowers’s is the third. A vivid example with the numbers discussed above:
in Conway, the third unit “eats” the remainder of the chain 3 → 3 → 1 → 2 = 3 → 3 = 27, then in Bowers it just “works” for its further growth: {3,3,1,2} = {3, 3, tritree}.

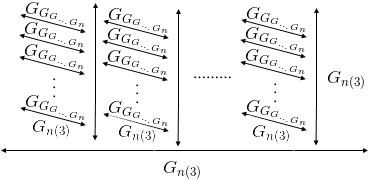
By the way, it was just an array of 4 elements. Add madness? It’s not interesting to simply increase the number of elements of the array separated by commas, following the already formulated rules for working with them. Therefore, Bowers comes up with modified “brackets” in order to at least “visualize” numbers in massive notation. The fourth number in the array still remains with curly braces, and then the disgrace begins: the fifth - square brackets rotated 90 degrees, the sixth - the rings around the previous design, the seventh - inverse angle brackets, the eighth - three-dimensional square ... In short, it's easier to show :

(you can also see similar pictures here )

Do you think Bowers stopped there? No matter how. Well, what else can you come up with in writing arrays? And you can pay attention that there are commas ... Which let them denote the elements of a one-dimensional array. And if you put between the numbers (1), then this is the transition to the next line, (2) - the transition to the next plane.
A square of triples (“dutritri”) is written as {3.3.3 (1) 3.3.3 (1) 3.3.3}.
Cube of triples (“Dimentry”) - {3.3.3 (1) 3.3.3 (1) 3.3.3 (2) 3.3.3 (1) 3.3.3 (1) 3.3.3 (2) 3.3.3 (1) 3.3.3 (1) 3.3.3}.

This is how unpretentiously we switched from planar to voluminous arrays (and note, this is just a record of a certain number, which because of its scale required to leave the plane simply in its spelling!). Of course, further we introduce new notation for four-dimensional, five-dimensional “objects” (sorry, it’s already difficult to call these monstrous constructions numbers). For example, & means "an array of": {10,100,2} & 10. That is, a {10,100,2} is an array of tens, or 10 ↑↑ a 100-array of tens. Well, that is, you need to raise ten to the tenth power 100 times, build a lattice with so many cells (moreover, it will be in hundredmeasurement, that is, measure measurements ... measurements (the word is repeated a hundred times)), then fill all the cells with dozens - and only then You can begin to solve this array.

Think at least that's all? Nope. Denote the "legion" by a forward slash (/). In the array {a, b, c, ... / 2}, the two are in the second legion. First we must solve the first legion (to the left of the slash), and then take the number of elements in the chain "array of ... array of ... array of ...", which turned out when solving: {3,3 / 2} = 3 & 3 & 3 = {3,3,3} & 3. But if you take {3,3,3 / 3} = {3 & 3 & 3/2}. This time, tritry is not the number of elements in the array, but the number of elements in the chain 3 & 3 & ... & 3 & 3.
Another extension Bowers made by adding the @ symbol (a @ b stands for “legion array of size a of b”) and backslash \ (l y gion). Well, here everything is clear: {a, b \ 2} = a @ a @ a ... a @ a @ a (where a is repeated b times).

Clear,for some operations it can’t be infinite (legions and lugions are followed by lagions, lions and ligions, but it’s obvious that this is nothing, given our scope), so Bowers made it easier - he defined L as a progression of legions, lugions, lagions, lions and ligions: L1, L2, L3 ... And then the number is overtaken by the indices.
For example, for “calculation” (it’s ridiculous, of course, to talk about calculations on such scales) {L100,10} _10,10you need to take the hundredth term in the progression “legions, lugions, lagions ...” and compose an array of 10 dimensions from it. Then you need to remove one member each time adding a chain of “10% 10% ...% 10” (where% is the L100-gion array from the number of tens that you obtained in the previous step. And only after all the hundredth members (as well as L99, L98 and others like them, right up to \ and /) we’ll be able to actually begin to solve the first array in a crazy progression of arrays.

By the way, for 340 large numbers Bowers introduced his own names, many of which are crazy fully comply with the calculation algorithms. Meet MEAMAAMEALOKKAPUVA UMPA: {{L100,10} _{1 0.10} & L, 10} _10.10 .

<sup>Note for nerds:
Of course, Bowers defined a strict set of rules for performing operations on arrays.
Definitions:
- the first record in the array is called the “base” (base) - b;
- the second record in the array is called "initial" (prime) - p;
- the first non-unit record after the initial one is called a “pilot”;
- the record of the array that immediately follows the pilot is called the “co-pilot”. It does not exist if the pilot is the first entry in his row;
- a structure is a part of an array that consists of groups of lower dimension. This can be a record (X 0 ), a series (X 1 ), a plane (X 2 ), a region (X 3 ), etc., not to mention structures of a larger dimension (X 5, X 6 , etc.) and tetrational structures, for example, X ↑↑ 3. You can also continue with pentational, hexation, etc. structures.
- “previous entry” (previous entry) is a record that is formed in front of the pilot, but in the same row as the other previous entries. “Previous row” is a row that appears in front of the pilot row, but in the same plane as all the other previous rows, etc.
- The “prime block” of structure S is computed by replacing all occurrences of X with p. For example, if S = X 3 , then the initial block will be p 3 or a cube with a side of length p. The initial block X of the x- structure will be p p , p-hypercube with side length p.
- “aircraft” includes the pilot, all previous entries, as well as the initial block of all previous structures;
- “passengers” are records in an airplane that are not a pilot or co-pilot;
- the value of the array is written as v (A) , where A is an array.
Calculation rules:
1. If p = 1, v (A) = b
2. If there is no pilot, then v (A) = b p
3. If the first and second are not applied, then:
- the pilot decreases by 1;
- the second pilot takes the value of the original array with the initial value reduced by 1;
- each passenger becomes b;
- the rest of the array does not change.
All the examples described above obey these simple rules.</sup>

As mentioned above, BEAF is significantly superior in power to Conway’s chains, not to mention Knuth’s notation ... I wonder what's next?

And then we enter the field of philosophy rather than mathematics proper. All the notations described above are computable functions or functions that can be implemented on a Turing machine.

In the second part, we will consider non-computable functions : the zealous beaver problem, the Rado sigma function Σ (n), the Rayo number, BIG FOOT and others, and also consider the fast-growing hierarchy to understand if there is a limit to this mathematical madness.

Materials used:
1. The main site on hugology: http://googology.wikia.com/wiki/Googology_Wiki
2.Jonathan Bowers Endless Scrapers
3. Exploding Array Function