Intervals in C ++, Part 3: Introducing Incrementors (Iterable)
- Transfer
In previous posts, I described the problems that I encountered when creating a library for working with intervals. Now I will describe to you my solution: improvements to the concept of intervals, which allow you to create intervals with delimiters and infinite intervals that fit perfectly into the hierarchy of the standard library without sacrificing performance.
At the end of the previous post, I summarized the shortcomings of the existing intervals:
The first problem is especially difficult, so let's start with it.
To get started, let's strictly define the concept of interval. In the C ++ standard, this word is used everywhere, but is not defined anywhere. You can understand that the interval is something from which you can extract begin and end, a pair of iterators that are arranged so that you can get to end by starting with begin. In terms of my proposal, this concept can be formalized as follows:
There are also improvements to the concept of the Range span called InputRange, ForwardRange, etc. In fact, they simply require more from their iterators. The whole hierarchy is shown below.
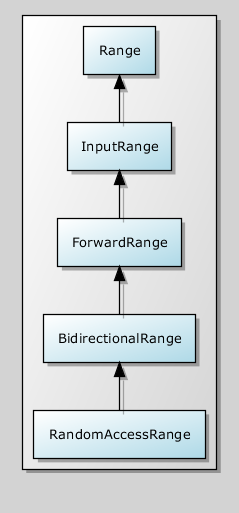
These concepts are the basis for the Boost.Range library (http://www.boost.org/libs/range)
If you remember, to implement intervals with both a limiter and infinite ones, in the form of a pair of iterators, the end iterator must be signal. And such an iterator is more of a concept than the physical position of an element in a sequence. You can imagine it as an element with the position "last + 1" - the only difference is that you do not know where his position is until you reach it. Since the type of signal iterator is the same as the usual one, a check at the program execution stage is required to determine if the given iterator is signal. This leads to slow iterator comparisons and inconvenient method implementations.
What are iterators for? We enlarge them, dereference and compare, right? And what can be done with the signal iterator? Not particularly much. His position does not change, he cannot be dereferenced, because his position is always "last + 1". But it can be compared with an iterator. It turns out that the signal iterator is a weak iterator.
The problem with the intervals is that we are trying to turn the signal iterator into a regular one. But he is not. So we will not do it - let them be of a different type .
The concept of Range requires that begin and end be of the same type. If you can make them different, it will already be a weaker concept - the concept of Iterable. Incrementors are like iterators, only begin and end have different types. Concept:
Naturally, the Range concept is part of the Iterable concept. She simply refines it by adding an equality constraint on the begin and end types.
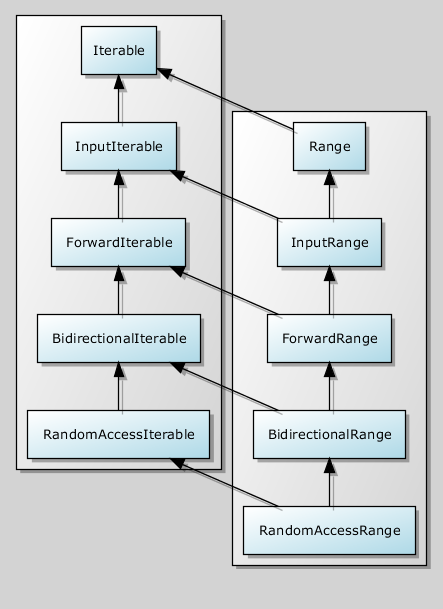
This is what the hierarchy looks like if we consider intervals, incrementors, and iterators, but it’s absolutely not necessary to define them in the program this way. Note that “interval” —that is, the similarity of the begin and end types — is orthogonal to the strength of the begin iterator. When we need to include RandomAccessRange modeling in the code, we can say requires RandomAccessIterable && Range and just change the whole concept.
The difference between, for example, BidirectionalIterable and ForwardIterable in the concept modeled by the begin iterable iterator.
But wait - STL algorithms will not work with incrementers, because they require that begin and end have the same type. And there is. So I went through the entire STL to check what could be rewritten. For example, std :: find
Now std :: find uses Ranges. But note that the algorithm does not try to change the position of the end iterator. The search algorithm can easily be changed to work with Iterables instead of Ranges:
That’s all - the change is so small that it’s even hard to notice.
So what C ++ 98 algorithms can be adapted to work with Iterables instead of Ranges? It turns out almost everything. It’s easier to list those that defy. It:
The remaining fifty require a purely mechanical change in the code. By defining the concept of Iterable as defined by Range, we give any algorithm that works with Iterable the ability to work with Ranges in the same way. This is useful and important - too much code has been written for iterators to make some kind of incompatible abstraction for them.
And what do we get? Let's get back to our C-lines. I described the c_string_range class and found that character enumeration generates bad code. Let's start again, only with range_facade to build Iterable instead of Range.
The code is much simpler than the old one. Range_facade does all the work. An iterator and a signal iterator are implemented as primitives. To test it, I generated optimized machine code for the following functions, one of which uses the old c_string_range class, and the other uses the new c_string_iterable:
Even without knowing the assembler, you can understand the difference.
The code with incrementors is much cooler. And it is almost identical with the assembler obtained from the iterator "bare" C .
But what does comparing two objects of different types for equivalence mean?
A little for the uninitiated: N3351 determines in which cases comparisons of different types are permissible. It is not enough that the syntax “x == y” be valid and produce a Boolean value. If x and y have different types, then these types must themselves be EqualityComparable, and they must have a common type to which they can be converted, and it must also be EqualityComparable. Suppose we are comparing char and short. This is possible because they are EqualityComparable, and they can be converted to an int, which is also EqualityComparable.
Iterators can be compared, and signal iterators are compared in a trivial way. The difficulty is to find a common type for them. In general, each iterator and signal have a common type, which can be created as follows: suppose the existence of a new type of iterator I, which is a type-sum, and contains either an iterator or a signal iterator. When they are compared, it behaves semantically as if they were both first converted to two objects of type I, let's call them lhs and rhs, and then compared by the following plate:
This plate resembles the one obtained when analyzing the behavior of the comparison operator c_string_range :: iterator . This is not accidental - it was a special case of this more general scheme. It confirms the intuitive conclusion that you can already notice by looking at my two classes, c_string_range and c_string_iterable. One is a pair of iterators, the other is a pair of iterator / signal, but their operation scheme is similar. We feel that it is possible to build an equivalent Range from any Iterable if you sacrifice a small bit of performance. And now we have found confirmation of this.
The ability to compare iterators and signal iterators directly allows us to use the C ++ type system to optimize a large category of iterations, removing branchings in the parity comparison operator.
The idea of giving different types of begin and end is not new, and it was not me who invented it. I learned about it from Dave Abrahams many years ago. Recently, a similar idea was presented by Dietmar Kuehl on the Ranges mailing list, and in response to his letter, Sean Parent objected:
If I understood him correctly, he talks about the existence of three parallel concepts of intervals: IteratorRange, CountedRange and SentinelRange. And these hierarchies do not need to try to relate to each other. The copy algorithm should contain three different implementations, one for each concept. Then you have to triple about 50 algorithms - and this is too much repetition in the code.
Even worse, some algorithms are based on refined concepts. For example, in libc ++, the rotate algorithm selects one of three implementations, depending on whether you pass it direct, bidirectional, or random access iterators. And to include three different implementations of Iterator, Counted and SentinelRanges, 9 rotate algorithms would be required! With all due respect, this is crazy.
At the beginning of the post I gave a list of problems associated with intervals with paired iterators. I showed a new concept, Iterable, which deals with performance issues, and raised the issue of the complexity of implementing intervals. So far I have not described how this concept works at infinite intervals, which we will talk about in the fourth, final post.
All code can be found in the github repository .
I would like to thank Andrew Sutton for helping with Concpets Lite syntax and for explaining the requirements of the EqualityComparable concept for different types and for general improvement and formalization of many ideas. Articles have become much better thanks to his great contribution.
Other articles in the series
Intervals in C ++, part 1: Intervals with delimiters
Intervals in C ++, part 2: Infinite intervals
Intervals in C ++, part 4: to infinity and beyond
At the end of the previous post, I summarized the shortcomings of the existing intervals:
- delimited intervals and infinite intervals generate bad code
- they have to model weaker concepts than they could
- you can easily pass an infinite interval into an algorithm that does not digest it
- they are difficult to use
- intervals that can be infinite or very large can cause overflow in difference_type
The first problem is especially difficult, so let's start with it.
Interval concept
To get started, let's strictly define the concept of interval. In the C ++ standard, this word is used everywhere, but is not defined anywhere. You can understand that the interval is something from which you can extract begin and end, a pair of iterators that are arranged so that you can get to end by starting with begin. In terms of my proposal, this concept can be formalized as follows:
using std::begin;
using std::end;
template
using Iterator_type =
decltype(begin(std::declval()));
template
concept bool Range =
requires(T range) {
{ begin(range) } -> Iterator_type;
{ end(range) } -> Iterator_type;
requires Iterator>;
};
There are also improvements to the concept of the Range span called InputRange, ForwardRange, etc. In fact, they simply require more from their iterators. The whole hierarchy is shown below.

These concepts are the basis for the Boost.Range library (http://www.boost.org/libs/range)
Problem 1: Bad Code Generation
If you remember, to implement intervals with both a limiter and infinite ones, in the form of a pair of iterators, the end iterator must be signal. And such an iterator is more of a concept than the physical position of an element in a sequence. You can imagine it as an element with the position "last + 1" - the only difference is that you do not know where his position is until you reach it. Since the type of signal iterator is the same as the usual one, a check at the program execution stage is required to determine if the given iterator is signal. This leads to slow iterator comparisons and inconvenient method implementations.
The concept of incrementors (Iterable)
What are iterators for? We enlarge them, dereference and compare, right? And what can be done with the signal iterator? Not particularly much. His position does not change, he cannot be dereferenced, because his position is always "last + 1". But it can be compared with an iterator. It turns out that the signal iterator is a weak iterator.
The problem with the intervals is that we are trying to turn the signal iterator into a regular one. But he is not. So we will not do it - let them be of a different type .
The concept of Range requires that begin and end be of the same type. If you can make them different, it will already be a weaker concept - the concept of Iterable. Incrementors are like iterators, only begin and end have different types. Concept:
template
using Sentinel_type =
decltype(end(std::declval()));
template
concept bool Iterable =
requires(T range) {
{ begin(range) } -> Iterator_type;
{ end(range) } -> Sentinel_type;
requires Iterator>;
requires EqualityComparable<
Iterator_type, Sentinel_type>;
};
template
concept bool Range =
Iteratable &&
Same, Sentinel_type>;
Naturally, the Range concept is part of the Iterable concept. She simply refines it by adding an equality constraint on the begin and end types.

This is what the hierarchy looks like if we consider intervals, incrementors, and iterators, but it’s absolutely not necessary to define them in the program this way. Note that “interval” —that is, the similarity of the begin and end types — is orthogonal to the strength of the begin iterator. When we need to include RandomAccessRange modeling in the code, we can say requires RandomAccessIterable && Range and just change the whole concept.
The difference between, for example, BidirectionalIterable and ForwardIterable in the concept modeled by the begin iterable iterator.
Iterable and STL Algorithms
But wait - STL algorithms will not work with incrementers, because they require that begin and end have the same type. And there is. So I went through the entire STL to check what could be rewritten. For example, std :: find
template
InputIterator
find(InputIterator first, InputIterator last,
Value const & value)
{
for (; first != last; ++first)
if (*first == value)
break;
return first;
}
Now std :: find uses Ranges. But note that the algorithm does not try to change the position of the end iterator. The search algorithm can easily be changed to work with Iterables instead of Ranges:
template
InputIterator
find(InputIterator first, Sentinel last,
Value const & value)
{
for (; first != last; ++first)
if (*first == value)
break;
return first;
}
That’s all - the change is so small that it’s even hard to notice.
So what C ++ 98 algorithms can be adapted to work with Iterables instead of Ranges? It turns out almost everything. It’s easier to list those that defy. It:
- copy_backward
- algorithms for working with sets and pyramids (push_heap, pop_heap, make_heap, sort_heap)
- inplace_merge
- nth_element
- partial_sort and partial_sort_copy
- next_permutation and prev_permutation
- random_shuffle
- reverse and reverse_copy
- sort and stable_sort
- stable_partition
The remaining fifty require a purely mechanical change in the code. By defining the concept of Iterable as defined by Range, we give any algorithm that works with Iterable the ability to work with Ranges in the same way. This is useful and important - too much code has been written for iterators to make some kind of incompatible abstraction for them.
Proof in Perf
And what do we get? Let's get back to our C-lines. I described the c_string_range class and found that character enumeration generates bad code. Let's start again, only with range_facade to build Iterable instead of Range.
using namespace ranges;
struct c_string_iterable
: range_facade
{
private:
friend range_core_access;
char const *sz_;
char const & current() const { return *sz_; }
void next() { ++sz_; }
bool done() const { return *sz_ == 0; }
bool equal(c_string_iterable const &that) const
{ return sz_ == that.sz_; }
public:
c_string_iterable(char const *sz)
: sz_(sz) {}
};
The code is much simpler than the old one. Range_facade does all the work. An iterator and a signal iterator are implemented as primitives. To test it, I generated optimized machine code for the following functions, one of which uses the old c_string_range class, and the other uses the new c_string_iterable:
// Range-based
int range_strlen(
c_string_range::iterator begin,
c_string_range::iterator end)
{
int i = 0;
for(; begin != end; ++begin)
++i;
return i;
}
// Iterable-based
int iterable_strlen(
range_iterator_t begin,
range_sentinel_t end)
{
int i = 0;
for(; begin != end; ++begin)
++i;
return i;
}
Even without knowing the assembler, you can understand the difference.
| |
The code with incrementors is much cooler. And it is almost identical with the assembler obtained from the iterator "bare" C .
Iterators, Signal Iterators, and Parity
But what does comparing two objects of different types for equivalence mean?
A little for the uninitiated: N3351 determines in which cases comparisons of different types are permissible. It is not enough that the syntax “x == y” be valid and produce a Boolean value. If x and y have different types, then these types must themselves be EqualityComparable, and they must have a common type to which they can be converted, and it must also be EqualityComparable. Suppose we are comparing char and short. This is possible because they are EqualityComparable, and they can be converted to an int, which is also EqualityComparable.
Iterators can be compared, and signal iterators are compared in a trivial way. The difficulty is to find a common type for them. In general, each iterator and signal have a common type, which can be created as follows: suppose the existence of a new type of iterator I, which is a type-sum, and contains either an iterator or a signal iterator. When they are compared, it behaves semantically as if they were both first converted to two objects of type I, let's call them lhs and rhs, and then compared by the following plate:
| lhs signal iterator? | rhs signal iterator? | lhs == rhs? |
| true | true | true |
| true | false | done (rhs.iter) |
| false | true | done (lhs.iter) |
| false | false | lhs.iter == rhs.iter |
This plate resembles the one obtained when analyzing the behavior of the comparison operator c_string_range :: iterator . This is not accidental - it was a special case of this more general scheme. It confirms the intuitive conclusion that you can already notice by looking at my two classes, c_string_range and c_string_iterable. One is a pair of iterators, the other is a pair of iterator / signal, but their operation scheme is similar. We feel that it is possible to build an equivalent Range from any Iterable if you sacrifice a small bit of performance. And now we have found confirmation of this.
The ability to compare iterators and signal iterators directly allows us to use the C ++ type system to optimize a large category of iterations, removing branchings in the parity comparison operator.
Objections
The idea of giving different types of begin and end is not new, and it was not me who invented it. I learned about it from Dave Abrahams many years ago. Recently, a similar idea was presented by Dietmar Kuehl on the Ranges mailing list, and in response to his letter, Sean Parent objected:
I think we put too much on iterators. Algorithms that work with endings based on checking a signal iterator or based on counting are different entities. See copy_n () and copy_sentinel ()
stlab.adobe.com/copy_8hpp.html
Regarding intervals - I'm sure you can build it with:
- pairs of iterators
- iterator and quantity
- iterator and signal
And in this case copy (r, out) can produce the desired algorithm.
If I understood him correctly, he talks about the existence of three parallel concepts of intervals: IteratorRange, CountedRange and SentinelRange. And these hierarchies do not need to try to relate to each other. The copy algorithm should contain three different implementations, one for each concept. Then you have to triple about 50 algorithms - and this is too much repetition in the code.
Even worse, some algorithms are based on refined concepts. For example, in libc ++, the rotate algorithm selects one of three implementations, depending on whether you pass it direct, bidirectional, or random access iterators. And to include three different implementations of Iterator, Counted and SentinelRanges, 9 rotate algorithms would be required! With all due respect, this is crazy.
Total
At the beginning of the post I gave a list of problems associated with intervals with paired iterators. I showed a new concept, Iterable, which deals with performance issues, and raised the issue of the complexity of implementing intervals. So far I have not described how this concept works at infinite intervals, which we will talk about in the fourth, final post.
All code can be found in the github repository .
Acknowledgments
I would like to thank Andrew Sutton for helping with Concpets Lite syntax and for explaining the requirements of the EqualityComparable concept for different types and for general improvement and formalization of many ideas. Articles have become much better thanks to his great contribution.
Other articles in the series
Intervals in C ++, part 1: Intervals with delimiters
Intervals in C ++, part 2: Infinite intervals
Intervals in C ++, part 4: to infinity and beyond
