Content

1. What is a tensor and why is it needed?
2. Vector and tensor operations. Tensor Ranks
3. Curvilinear coordinates
4. The dynamics of a point in tensor exposition
5. Actions on tensors and some other theoretical questions
6. Kinematics of a free solid. The nature of angular velocity
7. The final rotation of a solid. Properties of the rotation tensor and method of its calculation
8. On convolutions of the Levi-Civita tensor
9. The derivation of the angular velocity tensor through the parameters of the final rotation. Apply the head and Maxima
10. We get the angular velocity vector. Working on shortcomings
11. Acceleration of a body point in free movement. Angular acceleration of a solid
12. Rodrigue Hamilton Parameters in Solid State Kinematics
13. SKA Maxima in problems of transformation of tensor expressions. Angular velocity and acceleration in the parameters of Rodrigue Hamilton
14. Non-standard introduction to the dynamics of a rigid body
15. Proprietary Solid Motion
16. Properties of the inertia tensor of a solid
17. Sketch of a nut Janibekova
18. Mathematical modeling of the Janibekov effect

Introduction

Last time, we examined one of the ways to obtain differential equations of motion of a rigid body based on the d'Alembert principle. We settled on the general form of the equations of motion


However, having carefully looked at these equations, I should be criticized - the fact is that in these equations the number of unknowns is too large. The unknowns include the acceleration of the pole and the angular acceleration of the body , as well as the reaction of bonds . And if the body motion is limited by at least one connection, the number of unknown quantities in (1) and (2) exceeds the number of equations.

This is because the left-hand side of equations (1) and (2) contains the accelerations calculated for the case of free motion of the body, that is, they have excess coordinates. Therefore, system (1), (2) should be supplemented by constraint equations describing the constraints imposed by constraints on the coordinates, velocities, and accelerations of points on the body.

This is what we are going to do now - see what equations (1) and (2) turn into when adding the equations of constraints, and what the obtained equations give us in a practical sense.

1. The equations of motion of a free solid

A free body is called a body whose movement is not limited by bonds. Accordingly, unnecessary unknowns disappear in equations (1) and (2) and they turn into


And for a free body, it makes no sense to use an arbitrary pole - it is better to change the center of reduction of the systems of inertia to the center of mass of the body, writing down the equations of motion in a simpler form


Equations (5) and (6) are differential equations of the free motion of a rigid body. They can be resolved with respect to accelerations and integrated numerically under given initial conditions.

2. The equations of motion of a rigid body with one fixed point

Now suppose that the motion of the body is limited by a spherical hinge located at a point . Then, by choosing the pole at this fixed point, we can add the constraint equation




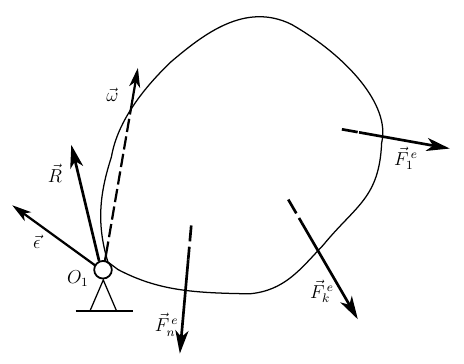
The reaction of the spherical joint is expressed by one force , therefore, taking into account (7), equations (1) and (2) can be rewritten in the form


moreover , since the force is applied at a point , then we finally get


Equation (8) allows you to determine the angular acceleration of the body, based on the initial conditions of the problem and the known active forces applied to the body, and equation (9) makes it possible, knowing the angular acceleration, to find the reaction of the spherical hinge. Thus we obtain differential equations of spherical motion.

3. Rotational movement of the body. The moment of inertia of the body about the axis

Rotational is the movement of a body when its two points remain motionless at any moment in time. If we express this fact using equations, then we can write the following equations of relations




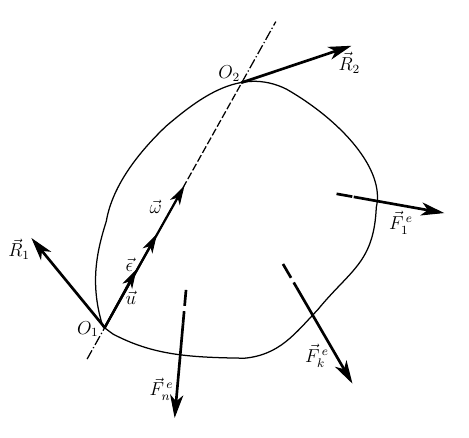
Condition (10) expresses the immobility of one of the points of the body, and condition (11) - the constancy of the direction of the axis of rotation of the body. Based on (11), we can write out the angular velocity and angular acceleration of the body through the parameters of the final rotation


We substitute (12) and (10) into equation (2)


given that we have two bonds, and accordingly two reactions from the bearings on which the body rotates. And you can immediately take into account that , since the first reaction is applied at a point . In addition, we perform scalar multiplication of the last equation by the unit vector of the rotation axis


We take into account that the moment of the second reaction can be calculated as , in this case , that is, we obtain


The second terms in both sides of this equation are mixed products of coplanar vectors and are equal to zero; as a result, we have


- differential equation of rotation of the body around a fixed axis, where


called the moment of inertia of the solid relative to the axis of rotation , and


- the projection of the vector moment relative to a fixed point on the axis passing through this point or - the moment of force relative to the axis .

Expression (14) is extremely interesting. If we rewrite it in tensor form, we get the formula


allowing, according to the well-known inertia tensor of a solid, to determine its moment of inertia relative to the axis of rotation of interest to us, the direction of which in space is given by the unit vector . The moment of inertia (16) is a scalar quantity characterizing the distribution of body mass around the axis of rotation. This quantity, as well as equation (13) are well known from the general course of theoretical mechanics.

4. The progressive movement of the body

In translational motion, the bonds imposed on the body impede its rotation. In this case, we can write down the obvious equalities


Assuming that bonds are ideal, we can write down the condition imposed on their reactions


where is the vector tangent to the trajectories of the points of the body. In the case of translational motion, the trajectories of all its points are the same, which means that the tangent vector to the trajectory is the same for all points. In view of (17) and (18), we can rewrite equation (1)


or


- the differential equation of the translational motion of the body in projections onto the tangent to the trajectories of its points.

Conclusion

In this article, we examined how the general equations of motion of a rigid body (1) and (2) are transformed if we supplement them with the equations of constraints. At the same time, we easily and naturally constructed differential equations of motion for all special cases of body motion studied by theoretical mechanics.

Acknowledgments

in preparing this article , the method proposed by the SeptiM user was used . In connection with the obvious convenience of work, I want to express my gratitude to the author for the work he has done.

To be continued...