Facebook World Data Analysis
- Transfer
Translation of Stephen Wolfram's post, Data Science of the Facebook World .
I express my deep gratitude to Kirill Guzenko for help with the translation.
alizar wrote a short note about this article and the Wolfram | Alpha and Wolfram Language features described therein. In our blog we provide its full translation.
Millions of people are currently using our Wolfram | Alpha Personal Analytics for Facebook app . And, as part of our latest update , in addition to collecting some anonymous statistics, we launched a “data donation” program that allows people to share with us the detailed data that we use for research purposes.
A few weeks ago, we decided to analyze all this data. And, I must say that, it was nothing more than a stunning example of the power of Mathematica and Wolfram language in data science (this is also good material for the data science course that I started to prepare).
We have always planned to use the data we collect to improve our personal analytics system . But I could not resist my attempts at the same time and consider all this from a scientific point of view.
I have always been interested in people and their life paths. But I never managed to combine this with my scientific interests. Up to this point. The past few weeks have been very exciting in observing the results we have received. Some were expected, while others were so unpredictable that I would never have imagined anything like that. And all this reminded of the phenomena from my work A New Kind of Science (New kind of science).
So what does the data look like? Below are the social networks of several data donors - groups of friends are divided by color (anyone can find their own network using Wolfram | Alpha or the SocialMediaData function in Mathematica ( in the latest version of Wolfram Language this function supports working with Facebook, GooglePlus, Instagram, LinkedIn, Twitter - approx.ed. )).

The first quantitative question is: how large are these networks? In other words, how many friends do people usually have on Facebook? Well, at least regarding users from our sample, this question is easy to answer. The median is 342, and below is a histogram showing the distribution (the graph is built on the interval [0; 5000], because this is the maximum number of friends on a personal page on Facebook):
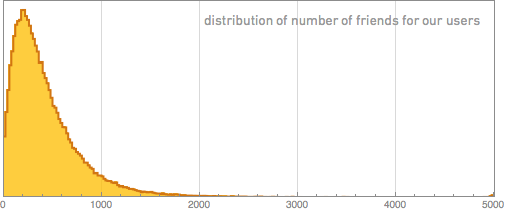
How typical are our users (in other words, how representative is our sample)? In many ways - as far as we can state it - they look pretty typical. But there are certainly some differences. Here is the distribution of the number of friends not only for our users, but also for their friends (there is a mathematical subtlety in the separation of these user sets, which I will talk about later):
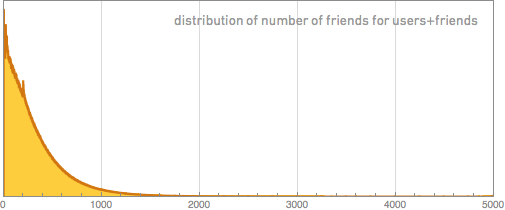
We see that in this wider population of Facebook users, there are significantly more people who have almost no Facebook friends. Whether such people should be included in examples is a moot point. However, judging by the results obtained, they do not have much influence (a sharp protrusion of 200 friends probably relates to the Facebook friend recommendation system.)
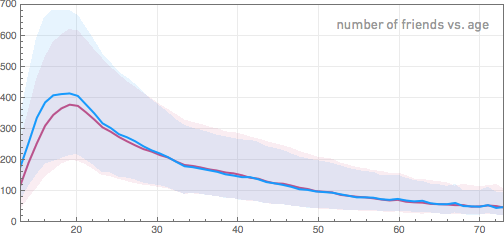
So, good. Let's see how the typical number of friends on Facebook changes with the age of the person. Of course, we all know how many people indicate their ages. However, let's still build a graph of the dependence of the number of friends of users on their age. The solid line indicates the average number of friends; consecutive bands indicate the corresponding octiles of the sample.
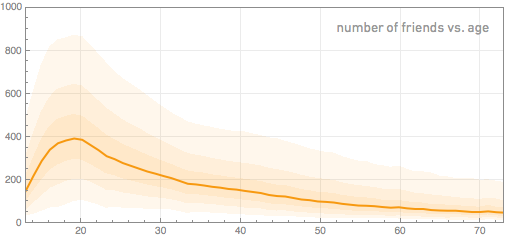
After rapid growth, there is a peak in the number of friends, which falls on young people a little younger than 20 years, after which there is a gradual decrease. Why it happens? I suspect that this is due to both the behavior of people and the fact that Facebook does not exist for so long. Assuming that people do not delete friends after they have added them, one would expect that the number of friends with increasing age should constantly grow. And the data are consistent with the results for young people. But there is a limit to growth, because the number of years during which people have a Facebook profile is limited. And if we assume that this does not depend on age, then from the graphs it follows that people add fewer people with age.
But what friends do they add? By taking a person of a certain age, we can, for example, build the distribution of the ages of his friends. Here are some of the results (the spasmodic nature of the graphs, especially for 70 years old, is a consequence of the limited amount of data we have):

And here is the animated version:
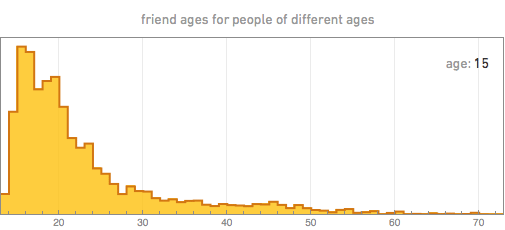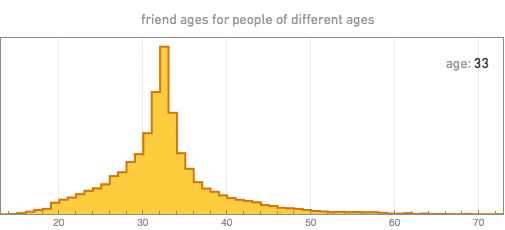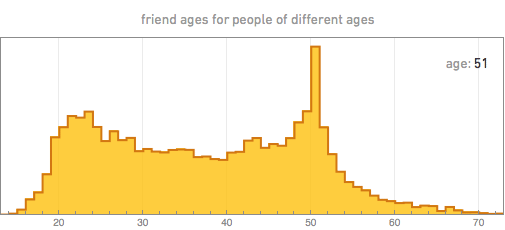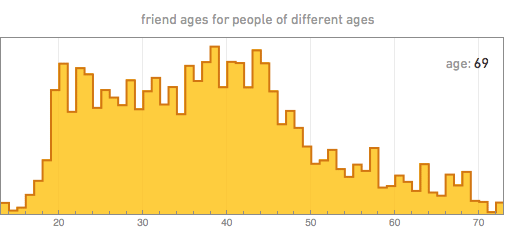
The first thing that catches your eye is that the age of friends always has a maximum near the age of the person himself, which probably reflects the fact that in modern society most friends appear in educational institutions and are of the same age. For younger people, the peak ages of friends are usually quite sharp. With age, the distribution of people gradually widens.
We can generalize all this by constructing the distribution of the ages of friends depending on the age of the person himself (a solid line shows the average age of friends):
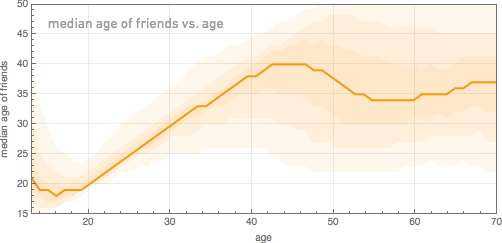
There is an anomaly for the youngest ages, apparently due to children under 13 who are unreliable about their age. But besides this, we see that young people, as a rule, have friends who are surprisingly close to them by age. The increase in the distribution width with an increase in the age of a person is probably due to the fact that in the workplace and in communities there is no such a rigid link to age as in educational institutions. And, from the graphs above, it turns out that by the middle of the fifth decade, people have a second peak in the younger age group, apparently because of their children who start using Facebook.
So what other information can be gleaned about people's lives? Here is a breakdown of the relationship statuses indicated in the profile, depending on age:
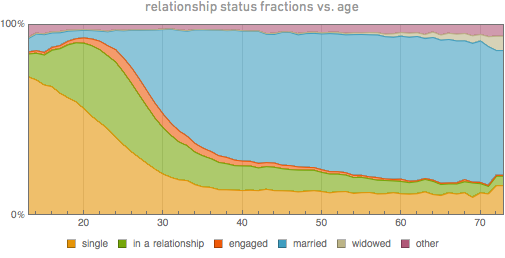
(from left to right: “lonely”, “dating”, “engaged”, “married”, “widowed”, “other”)
But in more detail, highlighting men (blue line) and women (purple line) (group “married + ”Includes both“ married ”, and“ in a civil marriage ”,“ divorced ”,“ widower / widow ”, etc.):
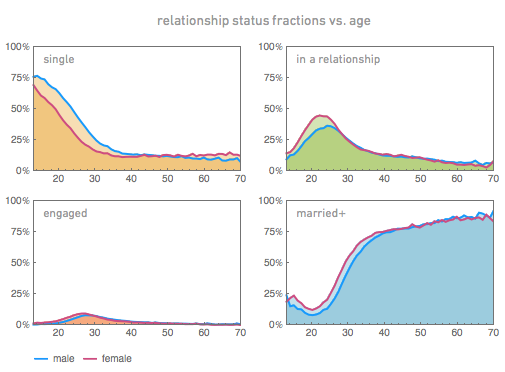
In children, there is some obvious absurdity (especially in girls) indicating that they are married. But overall, the trend is clear. The number of married people begins to increase in the third ten, moreover, a little earlier for women, and decreases at the end of the fourth ten, when about 70% of people are already married. The proportion of those in a relationship has a peak in the region of 24 years, and a small peak of the engaged is in the 27 years. The proportion of people who identified themselves as married continues to increase fairly linearly with age, reaching about 75% between 40 and 60 years, and the proportion of people who indicate their relationship status as single (single / single / lack of serious relationship; hereinafter - “not married / not married ”) continues to grow for women, while for men it decreases.
I must say that looking at the above graphs, I am amazed at their similarity with the graphs of physical processes like chemical reactions. As if people, despite the complexity of their behavior, are still somewhat similar to molecules that have a reaction rate for entering into relationships, marriage, and the like.
Of course, the above is true only for the Facebook world. And how does it compare with the world as a whole? Well, at least part of what we can learn in the Facebook world can also be found in official censuses. Here is an example of how our results for people married at certain ages correlate with the results of the official census of the United States (US Census - solid lines):

I am amazed at how much they converge. Although, obviously, there are some differences. Since some users under the age of 20 on Facebook unreliably indicate that they are married. And the elderly widows point to themselves on Facebook'e still married. For people over the age of 20, there is a slight systematic difference with people on Facebook - they get married on average a couple of years later than expected in the census (as you would expect, if you exclude the US rural population, the difference will be much smaller).
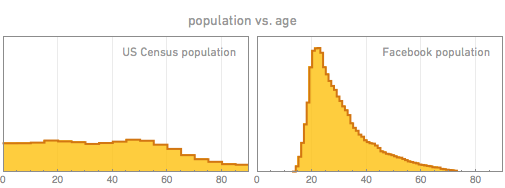
If we talk about the census, then we can ask ourselves how the totality of Facebook users correlates with the US population. And so, we get a rather expected roll of the aggregate of Facebook users towards young people:
Good. Above, we examined how a typical number of friends in a person depends on his age. What about gender? This may be somewhat surprising, but if we look at the charts for men and women, then we will not find a noticeable difference in the distributions of the number of friends. But if instead we consider the same thing depending on age, we can notice some differences:
Teenage boys tend to have more friends than teenage girls, perhaps because they are less selective about who to accept as friends. However, at the beginning of the third dozen, the difference between the sexes is quickly reduced.
What is the effect of relationship status? Here are data on men and women, depending on age:

For older people, marital status, perhaps, does not have much impact. But for young people it is having. Adolescents who (not) correctly identify themselves as married have, on average, more friends. And girls from a younger teenage group who identify themselves as “engaged” (possibly to be able to indicate their best friends in the status) usually have more friends than those who indicate their status as “unmarried”, or just "in a relationship."
A completely different story indicating your location on Facebook - this data is much more reliable. And often you can see quite strong differences depending on location. As in this comparison, the average number of friends in countries around the world (gray countries indicate insufficient data) and for US states:
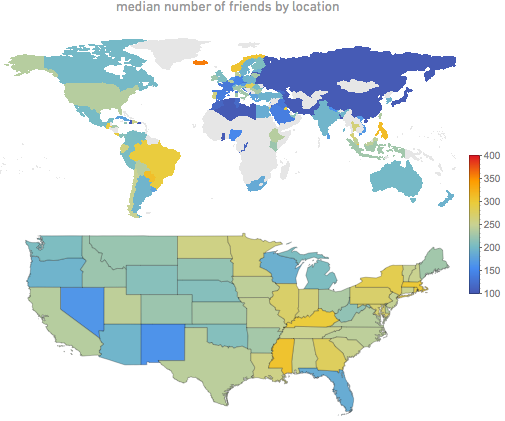
There are some interesting points. In countries such as Russia and China, the average number of friends is not particularly high, because Facebook is not widespread in them. And perhaps fewer friends in the western United States are due to low population density. But I can’t understand why the average number of friends is higher in Iceland, Brazil, the Philippines and the Mississippi (of course, there is some error due to people who incorrectly indicate their position, but taking into account the size of our sample, I don’t think that they have a big impact).
On Facebook, people can indicate both “hometown” and “city of current residence”. Here's how the likelihood that these items will be different with age changes:
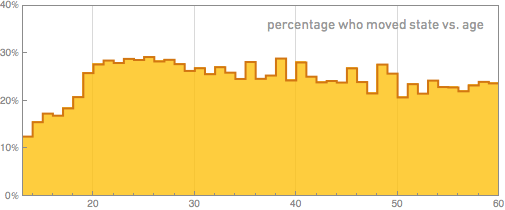
What we saw is pretty expected. For some part of the population there is a certain level of random movements, noticeable for younger ages. About 18 years old, there has been a jump when people leave their home, going to an educational institution. Some subsequently return and subsequently decide what will be considered their hometown.
One may wonder - where and where do people move from? Here's a graph showing the number of people in our collection of Facebook users moving between different US states and different countries:
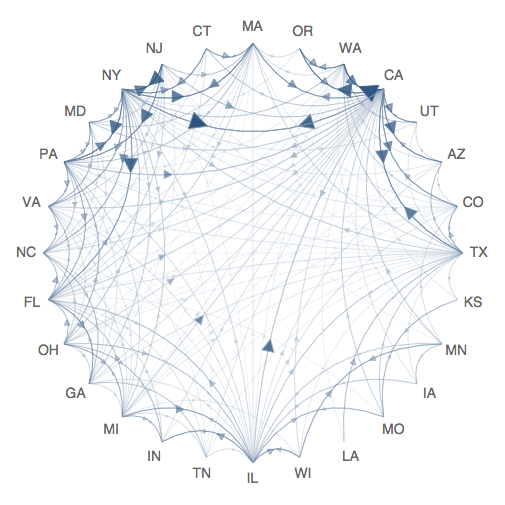

There are still a huge number of demographic issues that can be addressed. But let's get back to social networks. There is a general observation that people tend to be friends with people like themselves. Thus, in order to check this, we could, for example, find out whether people with a lot of friends tend to have people as “friends” in friends. Here is a graph of the average number of friends our users have as a function of the friendliness of their friends:
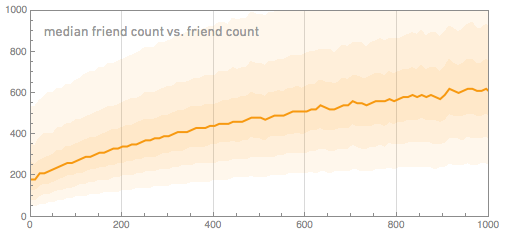
And the result is that the “friendliness” of people positively correlates with the “friendliness” of their friends. Although it can also be noted that usually “friendly” people have slightly less “friendly” friends.
And based on this, we can discuss some of the subtleties that I mentioned earlier. The very first graph in this post shows the distribution of the number of friends our users have. But what about the number of friends their friends have? If we simply take data on all the friends of all our users, we can thus compare the distribution of the number of friends of our users with the distribution of their friends:
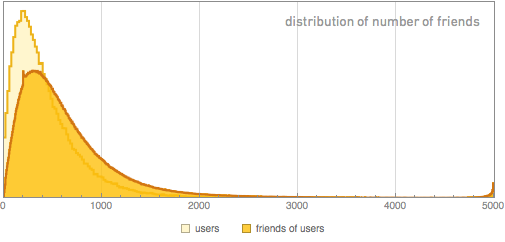
It seems that the friends of our users always have more friends than our users themselves. But in fact, given the data from the previous chart, we know that this is not so. So what's going on? This is a somewhat subtle, but common, social networking phenomenon, known as the "friendship paradox." The important point is that when we looked at the friends of our users, we inevitably chose the space of all Facebook users in a very heterogeneous way. In particular, if our users represent a homogeneous sample, then the frequency of choosing a friend will depend on how many friends they have, as a result of which people with a lot of friends will be selected more often, so the average number of friends will increase .
This problem can easily be dealt with by taking friends weighed depending on how many friends they have - this is what we have already done in this post. And if we do this, we will find out that in fact the friends of our users do not tend to have more friends than the users in question themselves; it turns out that the average number of friends they have is 229 instead of 342.
It is worth noting that if we look at the distribution of the number of friends that we got for the aggregate of Facebook users, we will notice that it is very well approximated by a power law with an indicator of -2.8. And this is the usual form for networks of various types, which can be understood as a consequence of the preferential attachment effect, in which, as the network grows, nodes that already have many connections have greater advantages for obtaining new connections, which leads to the limitations of scaleless networks with power parameters.
So good. Let's now take a closer look at the social networks of individual users. I don’t use Facebook very actively, so I don’t think my network will be interesting enough. However, my 15-year-old daughter Katerina was kind enough to provide her own network for review:
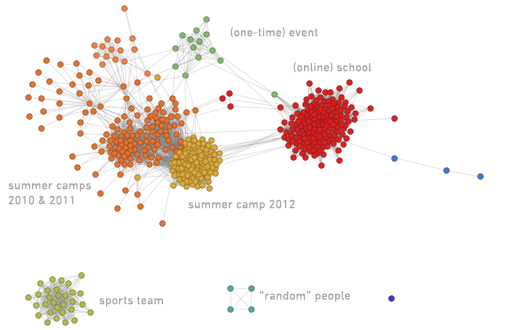
Each node of the network corresponds to Katerinin’s friend on Facebook, and the connection corresponds to the presence of a person in friends (there is no such node in the network that would correspond to Katerina, because she is connected with everyone). The network is built (using the Wolfram language FindGraphCommunities function ) to highlight groups or communities of friends. And it’s very surprising how this network “tells a story”. Each group corresponds to some part of Katerina’s life or her past.
Here is a complete selection of our data donor networks:

There is no doubt that each of these networks tells a story of its own. However, we can produce general statistics. For example, here is a graph of how the number of groups of friends changes with age (with more data, we would have less noise):
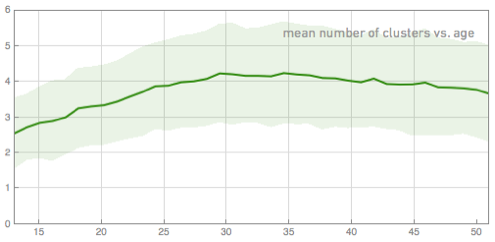
Even at the age of 13, people have approximately three groups of friends (probably friends from school, from the district, and family). When they get older, they move to other schools, get jobs, and so on, and as a result, other groups form. Now the maximum number is observed in the region of 30, probably largely due to the limited time of Facebook’s existence.
How large are these groups on average? The largest group usually contains about a hundred friends; the graph below shows the size dependence on age:
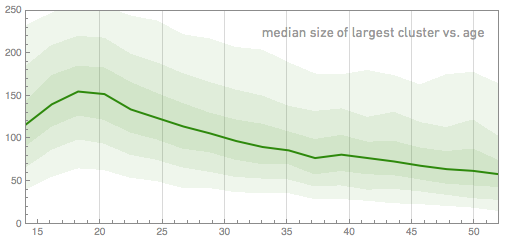
And here is how the proportion of the largest group in relation to the entire network changes with age:
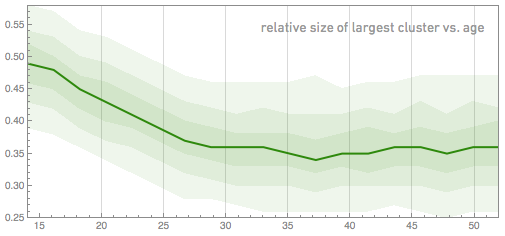
What about the more detailed properties of networks? Is there a “periodic table” of network structures? Or a classification scheme like the one I developed a long time ago for cellular automata?
The first step to finding something different in each network that we can do is consider their cluster structure, ignoring the substructures. Here, for example, in this way we can simplify Katerina’s network (which proposed this idea) to the level of a cluster diagram:
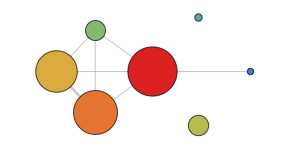
Below we show what we get by doing the same for data donor networks:
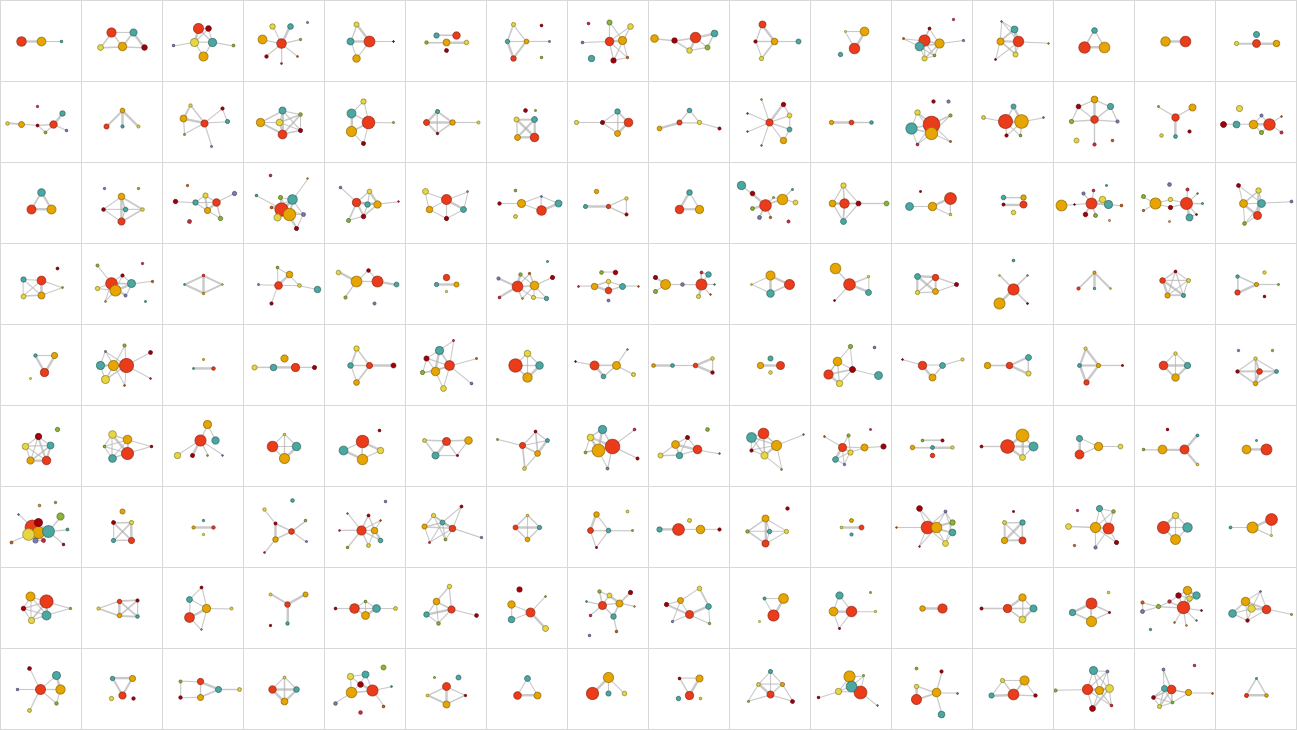
When creating these diagrams, we take for the cluster that group in which there are at least two friends. However, to obtain a more general structure, we can remove from consideration those clusters that contain less than 10% of the total number of friends. So, for example, then the network of Katerina will look like:
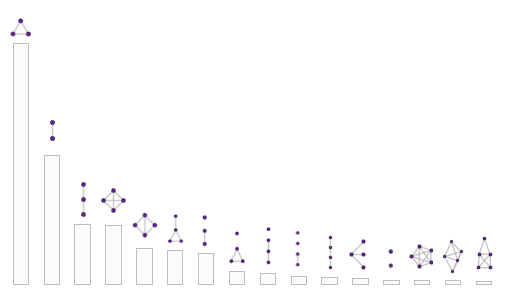
And now, for example, we can calculate the relative amounts of various types of structures that appear in all networks of data donors:
And we can consider how the proportion of each of the structures changes with age:

What did we learn from this? The most common structures consist of two or three main and interconnected clusters. But there are also structures in which the main clusters do not have any connections between themselves - apparently, this is a reflection of the presence in a person of such aspects of life that are not connected with each other due to geographical reasons or their content.
Each person has a story behind the structure of his cluster diagram. And you might think that all this cannot be generalized by any single theory. In a way, this is a bit like trying to develop a general theory of human history or the paths of biological evolution. But the interesting thing is that the Facebook world gives us much more data to formulate such theories.
And we do not just have to consider things like cluster diagrams, or even friendly networks - we can dig as deep as we like. For example, we can analyze the many posts of people that they post on their Facebook walls and sort them by topics (for this, we used a classifier of natural-language content written in Wolfram language and trained in a large sample):
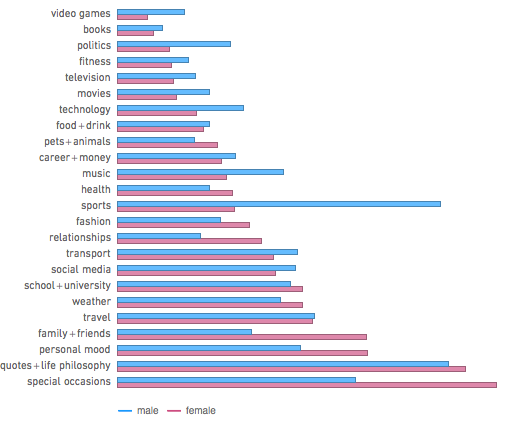
Each of these topics is characterized by specific, common words:

And for each topic, we can find out how its popularity depends on age (indicated on Facebook):
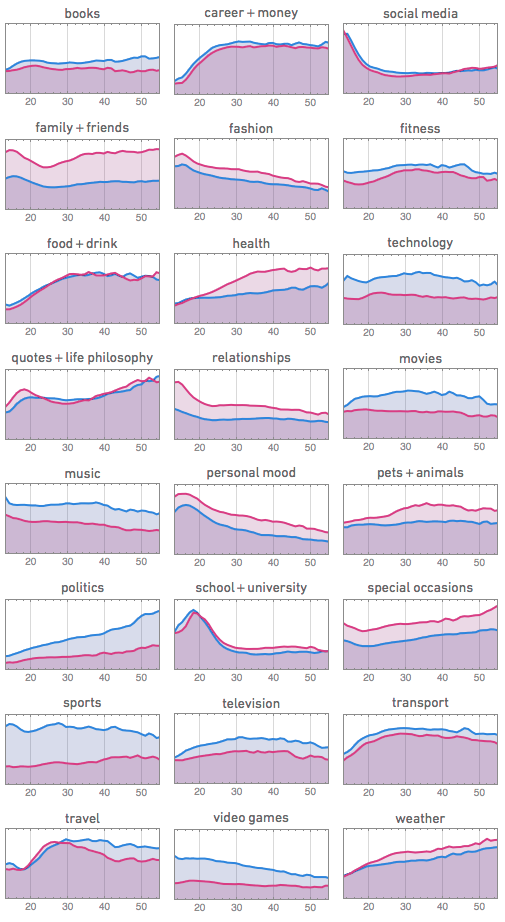
It is amazing how much information can be gleaned from this about the evolution of the typical interests of people. With age, people begin to talk less about video games and more about politics and weather. Men tend to talk more about sports and technology than women, and, which surprised me somewhat, they also begin to talk more about cinema, television and music. Women talk more about animals, family, friends, relationships, and, at least after they reach childbearing age, about health. It is not particularly surprising that the peak age of talk about school and university is 20 years. People are less interested in talking about “special cases” (mainly birthdays) in adolescence, but then interest in this topic increases. And in the third ten, people begin to talk much more about career and money. And so on and so forth.
Some things are depressingly stereotypical. And most of them are not particularly surprising for those who know the natural differences of people of different ages. However, it is noteworthy for me how clearly and in detail we can see on these graphs the reflection of people's thinking in the course of their lives.
Of course, the above charts are based on the completely anonymous data we have collected. But if we start to look at individuals, we will see many other interesting things. For example, I’m personally very curious to analyze my email archive for 25 years , and perhaps predict things about myself based on a comparison with what happens to people in general.
Over the decades, I have constantly accumulated countless case studies on the trajectories of people's lives, from which I have drawn a number of general patterns. But what was striking to me about what we did in the last few weeks is how much systematic information you can get at a time. What all this means, and what general theories can be built from all of this, I don’t know yet.
However, this is similar to the beginning of the creation of a powerful “computing telescope” exploring the “social universe”. And this allows us to explore and discover the most diverse phenomena. This has the potential to help us learn more about society and ourselves. And this, by the way, gives us excellent examples of what can be achieved with the science of data and with the technologies that I have been developing for so long.
