Python neural network vector implementation example
- Tutorial
The article will focus on the construction of neural networks (with regularization) with computations mainly in the vector way in Python. The article is close to the materials of the Machine learning by Andrew Ng course for a quicker perception, but if you didn’t take anything terrible, nothing specific is expected. If you always wanted to build your neural network with preference and young ladies vectors and regularization, but something was holding you back, then now is the time.
This article is aimed at the practical implementation of neural networks, and it is assumed that the reader is familiar with the theory (therefore, it will be omitted).
The code is commented in English, but it is unlikely that anyone will have difficulties, as the main comments are also given in the article in Russian.
We will write code to find the optimal weight values using scipy.optimize.fmin_cg, as well as on our own, so the scripts will be universal.
We will immediately proceed to practice, there are many articles on neural networks on Habré,
Software and dependencies
Python 3.4 (it will also work with minor
changes on 2.7) Numpy
SciPy (optional)
For the convenience of work, we will put all the functions of the neural network into a separate module network.py
The first thing that needs to be implemented is the creation of a fully connected neural network. In fact, this means that we need to initialize Theta θ weight matrices with random values from -1 to 1.
Since we create functions inside the network class, the function will actually have one layers variable that contains the number of layers and neurons in the created network in list format. For example [10, 5, 5, 1] means a network with ten input neurons, two hidden layers of 5 neurons each and an output layer with one neuron
Since the size of the layers variable is unlikely to exceed several tens of elements even in the most complex neural network, in this case the for loop is applicable.
As a result, we want to get a list of theta whose elements will be matrices with weights.
At this stage, we need to calculate the output signal of the neural network using the weights initialized in the previous step.
In short, using the np.vectorize command, a function can now accept and read value matrices. For example, for each element of a 10x1 matrix, a logistic function will be calculated and a matrix of values of 10x1 dimension will be returned
Of the important, I want to note that we add the bias column after we apply the activation function to the sum of the pieces. This means that bias is always equal to one, and not a logistic function of one (which is 0.73)
In addition, in the final matrix of activation functions, bias is present in all layers except the output layer, it contains only the output signals of the neural network (accordingly, the dimension of the matrix = number of examples * number of neurons in the output layer).
For those who are not familiar with python, I note that not copies of variables (for example, the neural network nn ) are passed to the runAll function, but references to them, so when we change the variable nn ['z'] = z we change our network nn despite not passing the variable nn back. As a result, this function ( runAll ) will return to us the matrix of output signals of the network (its dimension is the number of output neurons * 1) and change the matrices z and
a in a neural network variable.
The error of the output signal of a neural network with regularization is calculated according to the following formula The
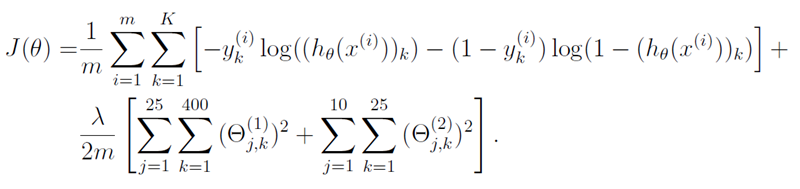
picture is taken from the materials of the Machine Learning course
m is the number of examples, K is the number of output neurons of the neural network, h0 (xi) is the vector of output values of the neural network, θ is the weight matrix, where θ ^ 1 weight matrix for the first hidden layer, lambda - regularization coefficient.
If it seems rather scary and incomprehensible to you, this is normal :), in essence, it decomposes into 2 components, with which we will work.
A detailed and understandable explanation of the essence of this formula will stretch out, and I'm not sure that it is necessary for such a prepared public, so for now let’s omit it, but write, if necessary, add it.
Actually, the error function will return us a single value in the float format, which will characterize how correctly our neural network calculates the output signal.
The function returns a neural network error for a given matrix X of input parameters.
Count the first part of the formula, directly the network error
Consider regularization
We allow a cycle through an array with theta matrices since it is assumed that we have a very limited number of layers, performance will not cause much damage.
We remove from the regularization the connection with the bias since it can very well be of great importance if we need to strongly shift the logistic function along the X axis.
At this stage, we can create a neural network, calculate the output signal and error, now it is only necessary to calculate the gradient and implement the algorithm for correcting weights.
At this step, we can not do without a cycle along the incoming vectors and in order to speed up the calculation of the gradient a little, we take out a maximum of operations before the cycle. For example, in the previous steps, we specially designed the runAll function in such a way that it would calculate the matrix of input values, and not the vector (row) individually, at this stage we will calculate the output values in advance, then we will access them in a loop. According to experimental measurements, these features accelerate the function by an additional 25%
We use the reverse cycle through the layers of the neural network from the last to the first, since we need to calculate the error and pass it back to the layer to calculate the next, etc.
The main difficulty is not to get confused in variable indices. For example, in most documentation on neural networks for for example a three-layer network (with one hidden layer), the error delta of the output layer will have an index of 3, it is clear that in this case the sheet should consist of four elements, while the gradient sheet consists of 3 elements.
The function returns a sheet whose elements are matrices whose dimensions match the dimension of theta matrices.
At the same time, this lambda function is nothing more than a derivative of an activation function (sigmoid), so if you want to replace the activation function, change also the derivative
Now we can test our neural network and even try to teach it something :)
First, we will teach our network simple segmentation, all values within [0; 5) are zero, [5; 9] are one
Result. The output of the neural network before training, training and after training. It can be seen that after training, the first five values are closer to zero, the second five are closer to unity.
In the previous example, the training was controlled by the fmin_cg function , now we will change theta (network weights) independently.
We set a simple task, to distinguish an upward trend from a downward trend. A neural network will receive 4 numbers at the input, if they increase sequentially, it is one, if they decrease, it is zero.
After 400 iterations (approximately 1 min.), For some reason, the last test case had the highest error (output of the neural network 0.13), most likely in this case it would help to add training data to improve the quality.
In the cycle, we change theta in order to achieve the maximum result. It turns out that we are kind of slipping to the local minimum of the function (and if we added the gradient, we would go to the local maximum). The alf variable , often called the "learning speed", is responsible for how much we will change theta in each iteration. However, if you set the alpha parametertoo large, the network error may even increase or jump up and down since the function will simply step over the local minimum.
As you can see, the entire neural network consists of one variable of the dict type, so it is easy to serilize, and save it in a simple text file and restore it for future use.
Perhaps the next publication will be on the topic of how to speed up this code (and any other written in Python) using GPU computing
UPD
Thanks to everyone who pluses.
This article is aimed at the practical implementation of neural networks, and it is assumed that the reader is familiar with the theory (therefore, it will be omitted).
The code is commented in English, but it is unlikely that anyone will have difficulties, as the main comments are also given in the article in Russian.
We will write code to find the optimal weight values using scipy.optimize.fmin_cg, as well as on our own, so the scripts will be universal.
What vectors are we talking about and why are they needed?
Suppose a simple task is to add in pairs the elements of two one-dimensional arrays. We can solve this problem in a loop with enumerating all the values of arrays or add two vectors. Consider the following code.
On a simple laptop, the cycle is processed on average in 4 seconds. 40 mil sec Vectors stack in 0.02 seconds.
About the same difference in speed with other arithmetic operations. Not to mention the visualization of the code.
import numpy as np
import time
A = np.random.rand(1000000, 1) # Создаём вертикальный вектор 1 млн. строк и 1 столбец с рандомными числами float
B = np.random.rand(1000000, 1) # ----
C1 = np.empty((1000000, 1)) # Создаём вертикальный вектор 1 млн. строк и 1 столбец с пустыми значениями
C2 = np.empty((1000000, 1)) # Создаём вертикальный вектор 1 млн. строк и 1 столбец с пустыми значениями
start = time.time()
for i in range(0, len(A)):
C1[i] = A[i] * B[i] # Складываем каждый элемент векторов A, B и записываем сумму в соответствующую строку вектора C
print(time.time() - start)
start = time.time()
C2 = A + B #Складываем два вектора напрямую
print(time.time() - start)
if (C1 == C2).all(): # Проверяем на равенство все значения массивов
print('Equal!')
On a simple laptop, the cycle is processed on average in 4 seconds. 40 mil sec Vectors stack in 0.02 seconds.
About the same difference in speed with other arithmetic operations. Not to mention the visualization of the code.
We will immediately proceed to practice, there are many articles on neural networks on Habré,
for example these
Software and dependencies
Python 3.4 (it will also work with minor
changes on 2.7) Numpy
SciPy (optional)
For the convenience of work, we will put all the functions of the neural network into a separate module network.py
Network creation
The first thing that needs to be implemented is the creation of a fully connected neural network. In fact, this means that we need to initialize Theta θ weight matrices with random values from -1 to 1.
Since we create functions inside the network class, the function will actually have one layers variable that contains the number of layers and neurons in the created network in list format. For example [10, 5, 5, 1] means a network with ten input neurons, two hidden layers of 5 neurons each and an output layer with one neuron
def create(self, layers):
theta=[0]
for i in range(1, len(layers)): # for each layer from the first (skip zero layer!)
theta.append(np.mat(np.random.uniform(-1, 1, (layers[i], layers[i-1]+1)))) # create nxM+1 matrix (+bias!) with random floats in range [-1; 1]
nn={'theta':theta,'structure':layers}
return nn
Since the size of the layers variable is unlikely to exceed several tens of elements even in the most complex neural network, in this case the for loop is applicable.
As a result, we want to get a list of theta whose elements will be matrices with weights.
Why do we initialize theta [0] = 0?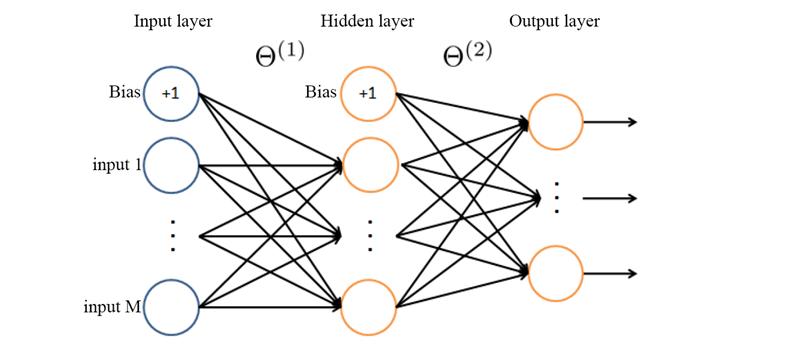
Image from the materials of the Machine Learning course, with improvements
In the field of neural networks, it is customary to call the θ1 matrix of weights from the input data to the first neural layer. Since we do not have any layers before the Input layer, then there is no zero matrix of weights either.

Image from the materials of the Machine Learning course, with improvements
In the field of neural networks, it is customary to call the θ1 matrix of weights from the input data to the first neural layer. Since we do not have any layers before the Input layer, then there is no zero matrix of weights either.
What is theta [1], theta [2], ..., theta [n]?
All matrices are compiled according to one algorithm, so let us consider theta [1] as an example. Theta [1] is a matrix in which the number of rows is equal to the number of neurons in the first hidden layer, and the number of columns is equal to the column for bias (offset) + the number of neurons in the input layer.
That is, if we take the first row of theta matrix [1], then the zero element (read the zero column) will correspond to the weight of the bias, the remaining elements (columns) will correspond to the weights for communication with each element of the input layer.
That is, if we take the first row of theta matrix [1], then the zero element (read the zero column) will correspond to the weight of the bias, the remaining elements (columns) will correspond to the weights for communication with each element of the input layer.
What is Bias and why is it needed?
Bias is translated from English as “bias” and in fact this is what it means (always yours, Cap). Better than here, I’m unlikely to say, so I’ll just do the translation.
Bias is almost always useful because it allows you to shift the activation function left or right , which can be extremely important for successful learning.
A simple example will help to understand. Imagine a simple neural network without a hidden layer, only one incoming and 1 outgoing neuron.
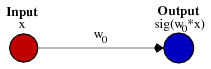
The output signal of the neural network is calculated by multiplying the weight W0 by the signal X and applying the activation function (most often a sigmoid) to the product.
An example of the functions that we obtain for different values of the weight W0

By changing the value of the weight W0, we change the slope of the curve, the degree of its steepness, this is convenient, but what if we need the outgoing signal to be 0 when X is 2? Just changing the slope of the curve does not work - it does not work to shift the entire curve to the right .
This is exactly what Bias does. If we add Bias to our neural network, for example:
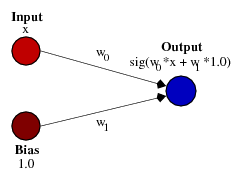
... then the output signal of our neural network will be considered sig (w0 * x + w1 * 1.0). Accordingly, our function will look like this when changing the weight of W1: A
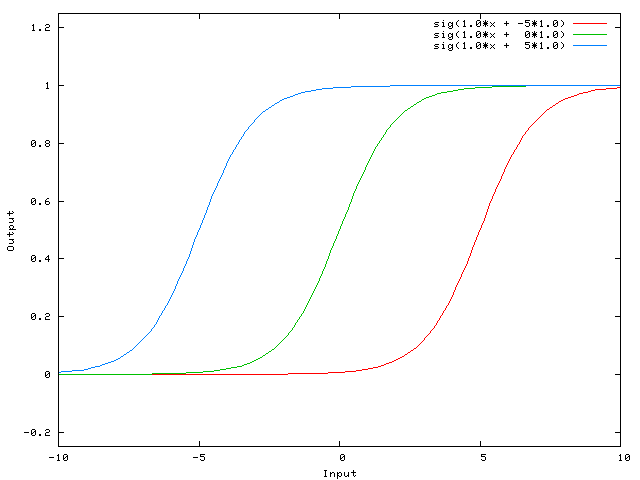
weight of W1 equal to -5 will shift the curve to the right, so the output signal of the neural network will be 0 when X is 2
Bias is almost always useful because it allows you to shift the activation function left or right , which can be extremely important for successful learning.
A simple example will help to understand. Imagine a simple neural network without a hidden layer, only one incoming and 1 outgoing neuron.
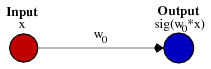
The output signal of the neural network is calculated by multiplying the weight W0 by the signal X and applying the activation function (most often a sigmoid) to the product.
An example of the functions that we obtain for different values of the weight W0

By changing the value of the weight W0, we change the slope of the curve, the degree of its steepness, this is convenient, but what if we need the outgoing signal to be 0 when X is 2? Just changing the slope of the curve does not work - it does not work to shift the entire curve to the right .
This is exactly what Bias does. If we add Bias to our neural network, for example:

... then the output signal of our neural network will be considered sig (w0 * x + w1 * 1.0). Accordingly, our function will look like this when changing the weight of W1: A

weight of W1 equal to -5 will shift the curve to the right, so the output signal of the neural network will be 0 when X is 2
Calculation of the outgoing signal of the neural network
At this stage, we need to calculate the output signal of the neural network using the weights initialized in the previous step.
def runAll(self, nn, X):
z=[0]
m = len(X)
a = [ copy.deepcopy(X) ] # a[0] is equal to the first input values
logFunc = self.logisticFunctionVectorize()
for i in range(1, len(nn['structure'])): # for each layer except the input
a[i-1] = np.c_[ np.ones(m), a[i-1]]; # add bias column to the previous matrix of activation functions
z.append(a[i-1]*nn['theta'][i].T) # for all neurons in current layer multiply corresponds neurons
# in previous layers by the appropriate weights and sum the productions
a.append(logFunc(z[i])) # apply activation function for each value
nn['z'] = z
nn['a'] = a
return a[len(nn['structure'])-1]
More detailed description of variables
The format of the matrix X : rows are the vector of input values, columns are elements of the vectors.
Z is a sheet with matrices of sums of products of the values of the activation function from the previous layer and the weights connecting them to the current layer by a neuron. Input values do not need to use an activation function, they do not have weights, so we skip z [0] and start with z [1]
a is a sheet with matrices of activation function values
a [0] is a matrix containing bias (a unit vector of dimension m * 1) and input vectors X, that is, its dimension is the number of rows in X * (1 + the number of columns in X). Accordingly, a [1] contains a matrix of the value of activation functions in the first hidden layer, its dimension is the number of rows in X * (1 + the number of neurons in the first hidden layer)
Z is a sheet with matrices of sums of products of the values of the activation function from the previous layer and the weights connecting them to the current layer by a neuron. Input values do not need to use an activation function, they do not have weights, so we skip z [0] and start with z [1]
a is a sheet with matrices of activation function values
a [0] is a matrix containing bias (a unit vector of dimension m * 1) and input vectors X, that is, its dimension is the number of rows in X * (1 + the number of columns in X). Accordingly, a [1] contains a matrix of the value of activation functions in the first hidden layer, its dimension is the number of rows in X * (1 + the number of neurons in the first hidden layer)
def logisticFunction(self, x):
a = 1/(1+np.exp(-x))
if a == 1: a = 0.99999 #make smallest step to the direction of zero
elif a == 0: a = 0.00001 # It is possible to use np.nextafter(0, 1) and
#make smallest step to the direction of one, but sometimes this step is too small and other algorithms fail :)
return a
def logisticFunctionVectorize(self):
return np.vectorize(self.logisticFunction)
In short, using the np.vectorize command, a function can now accept and read value matrices. For example, for each element of a 10x1 matrix, a logistic function will be calculated and a matrix of values of 10x1 dimension will be returned
What are these conditions in the logisticFunction?
In the code above, there is one important pitfall associated with rounding (here you have to run ahead). Suppose that you are preparing a large network, many layers, many neurons, you initialized weights randomly and it turns out that the sum of the products on the output layer for each neuron is very small, for example -40. The logistic function from -40 will happily return you one.
Next, we will need to calculate the error of our neural network and we will transfer this unit to calculate the logarithm of 1 - the output value [log (1-output)] naturally the logarithm of the unit is not determined, but the error will not pop up, just our neural network will not train.
Next, we will need to calculate the error of our neural network and we will transfer this unit to calculate the logarithm of 1 - the output value [log (1-output)] naturally the logarithm of the unit is not determined, but the error will not pop up, just our neural network will not train.
Of the important, I want to note that we add the bias column after we apply the activation function to the sum of the pieces. This means that bias is always equal to one, and not a logistic function of one (which is 0.73)
a[i-1] = np.c_[ np.ones(m), a[i-1]];
In addition, in the final matrix of activation functions, bias is present in all layers except the output layer, it contains only the output signals of the neural network (accordingly, the dimension of the matrix = number of examples * number of neurons in the output layer).
For those who are not familiar with python, I note that not copies of variables (for example, the neural network nn ) are passed to the runAll function, but references to them, so when we change the variable nn ['z'] = z we change our network nn despite not passing the variable nn back. As a result, this function ( runAll ) will return to us the matrix of output signals of the network (its dimension is the number of output neurons * 1) and change the matrices z and
a in a neural network variable.
Neural network error
The error of the output signal of a neural network with regularization is calculated according to the following formula The
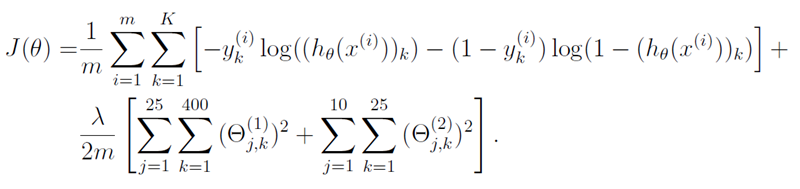
picture is taken from the materials of the Machine Learning course
m is the number of examples, K is the number of output neurons of the neural network, h0 (xi) is the vector of output values of the neural network, θ is the weight matrix, where θ ^ 1 weight matrix for the first hidden layer, lambda - regularization coefficient.
If it seems rather scary and incomprehensible to you, this is normal :), in essence, it decomposes into 2 components, with which we will work.
A detailed and understandable explanation of the essence of this formula will stretch out, and I'm not sure that it is necessary for such a prepared public, so for now let’s omit it, but write, if necessary, add it.
What is the essence of regularization?
The second line of the formula is responsible for regularization, the larger the regularization parameter, the greater the error of the neural network (since the sum of two positive numbers occurs in the whole formula), therefore, in order to reduce the error, it will be necessary to reduce the weight of the neural network, that is, a high regularization coefficient will keep the weights of the neural network small.
Actually, the error function will return us a single value in the float format, which will characterize how correctly our neural network calculates the output signal.
def costTotal(self, theta, nn, X, y, lamb):
m = len(X)
#following string is for fmin_cg computaton
if type(theta) == np.ndarray: nn['theta'] = self.roll(theta, nn['structure'])
y = np.matrix(copy.deepcopy(y))
hAll = self.runAll(nn, X) #feed forward to obtain output of neural network
cost = self.cost(hAll, y)
return cost/m+(lamb/(2*m))*self.regul(nn['theta']) #apply regularization
The function returns a neural network error for a given matrix X of input parameters.
Count the first part of the formula, directly the network error
def cost(self, h, y):
logH=np.log(h)
log1H=np.log(1-h)
cost=-1*y.T*logH-(1-y.T)*log1H #transpose y for matrix multiplication
return cost.sum(axis=0).sum(axis=1) # sum matrix of costs for each output neuron and input vector
Consider regularization
def regul(self, theta):
reg=0
thetaLocal=copy.deepcopy(theta)
for i in range(1,len(thetaLocal)):
thetaLocal[i]=np.delete(thetaLocal[i],0,1) # delete bias connection
thetaLocal[i]=np.power(thetaLocal[i], 2) # square the values because they can be negative
reg+=thetaLocal[i].sum(axis=0).sum(axis=1) # sum at first rows, than columns
return reg
We allow a cycle through an array with theta matrices since it is assumed that we have a very limited number of layers, performance will not cause much damage.
We remove from the regularization the connection with the bias since it can very well be of great importance if we need to strongly shift the logistic function along the X axis.
Gradient calculation
At this stage, we can create a neural network, calculate the output signal and error, now it is only necessary to calculate the gradient and implement the algorithm for correcting weights.
At this step, we can not do without a cycle along the incoming vectors and in order to speed up the calculation of the gradient a little, we take out a maximum of operations before the cycle. For example, in the previous steps, we specially designed the runAll function in such a way that it would calculate the matrix of input values, and not the vector (row) individually, at this stage we will calculate the output values in advance, then we will access them in a loop. According to experimental measurements, these features accelerate the function by an additional 25%
We use the reverse cycle through the layers of the neural network from the last to the first, since we need to calculate the error and pass it back to the layer to calculate the next, etc.
The main difficulty is not to get confused in variable indices. For example, in most documentation on neural networks for for example a three-layer network (with one hidden layer), the error delta of the output layer will have an index of 3, it is clear that in this case the sheet should consist of four elements, while the gradient sheet consists of 3 elements.
def backpropagation(self, theta, nn, X, y, lamb):
layersNumb=len(nn['structure'])
thetaDelta = [0]*(layersNumb)
m=len(X)
#calculate matrix of outpit values for all input vectors X
hLoc = copy.deepcopy(self.runAll(nn, X))
yLoc=np.matrix(y)
thetaLoc = copy.deepcopy(nn['theta'])
derFunct=np.vectorize(lambda x: (1/(1+np.exp(-x)))*(1-(1/(1+np.exp(-x)))) )
zLoc = copy.deepcopy(nn['z'])
aLoc = copy.deepcopy(nn['a'])
for n in range(0, len(X)):
delta = [0]*(layersNumb+1) #fill list with zeros
delta[len(delta)-1]=(hLoc[n].T-yLoc[n].T) #calculate delta of error of output layer
for i in range(layersNumb-1, 0, -1):
if i>1: # we can not calculate delta[0] because we don't have theta[0] (and even we don't need it)
z = zLoc[i-1][n]
z = np.c_[ [[1]], z ] #add one for correct matrix multiplication
delta[i]=np.multiply(thetaLoc[i].T*delta[i+1],derFunct(z).T)
delta[i]=delta[i][1:]
thetaDelta[i] = thetaDelta[i] + delta[i+1]*aLoc[i-1][n]
for i in range(1, len(thetaDelta)):
thetaDelta[i]=thetaDelta[i]/m
thetaDelta[i][:,1:]=thetaDelta[i][:,1:]+thetaLoc[i][:,1:]*(lamb/m) #regularization
if type(theta) == np.ndarray: return np.asarray(self.unroll(thetaDelta)).reshape(-1) # to work also with fmin_cg
return thetaDelta
The function returns a sheet whose elements are matrices whose dimensions match the dimension of theta matrices.
At the same time, this lambda function is nothing more than a derivative of an activation function (sigmoid), so if you want to replace the activation function, change also the derivative
lambda x: (1/(1+np.exp(-x)))*(1-(1/(1+np.exp(-x))))
Testing
Now we can test our neural network and even try to teach it something :)
First, we will teach our network simple segmentation, all values within [0; 5) are zero, [5; 9] are one
nn=nt.create([1, 1000, 1])
lamb=0.3
cost=1
alf = 0.2
xTrain = [[0], [1], [1.9], [2], [3], [3.31], [4], [4.7], [5], [5.1], [6], [7], [8], [9]]
yTrain = [[0], [0], [0], [0], [0], [0], [0], [0], [1], [1], [1], [1], [1], [1]]
xTest= [[0.4], [1.51], [2.6], [3.23], [4.87], [5.78], [6.334], [7.667], [8.22], [9.1]]
yTest = [[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]
theta = nt.unroll(nn['theta'])
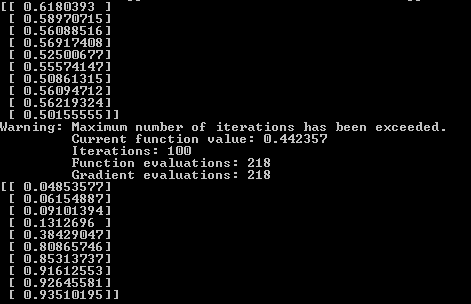
print(nt.runAll(nn, xTest))
theta = optimize.fmin_cg(nt.costTotal, fprime=nt.backpropagation,
x0=theta, args=(nn, xTrain, yTrain, lamb), maxiter=200)
print(nt.runAll(nn, xTest))
Result. The output of the neural network before training, training and after training. It can be seen that after training, the first five values are closer to zero, the second five are closer to unity.

In the previous example, the training was controlled by the fmin_cg function , now we will change theta (network weights) independently.
We set a simple task, to distinguish an upward trend from a downward trend. A neural network will receive 4 numbers at the input, if they increase sequentially, it is one, if they decrease, it is zero.
nn=nt.create([4, 1000, 1])
lamb=0.3
cost=1
alf = 0.2
xTrain = [[1, 2.3, 4.5, 5.3], [1.1, 1.3, 2.4, 2.4], [1.9, 1.7, 1.5, 1.3], [2.3, 2.9, 3.3, 4.9], [3, 5.2, 6.1, 8.2], [3.31, 2.9, 2.4, 1.5], [4.9, 5.7, 6.1, 6.3],
[4.85, 5.0, 7.2, 8.1], [5.9, 5.3, 4.2, 3.3], [7.7, 5.4, 4.3, 3.9], [6.7, 5.3, 3.2, 1.4], [7.1, 8.6, 9.1, 9.9], [8.5, 7.4, 6.3, 4.1], [9.8, 5.3, 3.1, 2.9]]
yTrain = [[1], [1], [0], [1], [1], [0], [1],
[1], [0], [0], [0], [1], [0], [0]]
xTest= [[0.4, 1.9, 2.5, 3.1], [1.51, 2.0, 2.4, 3.8], [2.6, 5.1, 6.2, 7.2], [3.23, 4.1, 4.3, 4.9], [7.1, 7.6, 8.2, 9.3],
[5.78, 5.1, 4.5, 3.55], [6.33, 4.8, 3.4, 2.5], [7.67, 6.45, 5.8, 4.31], [8.22, 6.32, 5.87, 3.59], [9.1, 8.5, 7.7, 6.1]]
yTest = [[1], [1], [1], [1], [1],
[0], [0], [0], [0], [0]]
while cost>0:
cost=nt.costTotal(False, nn, xTrain, yTrain, lamb)
costTest=nt.costTotal(False, nn, xTest, yTest, lamb)
delta=nt.backpropagation(False, nn, xTrain, yTrain, lamb)
nn['theta']=[nn['theta'][i]-alf*delta[i] for i in range(0,len(nn['theta']))]
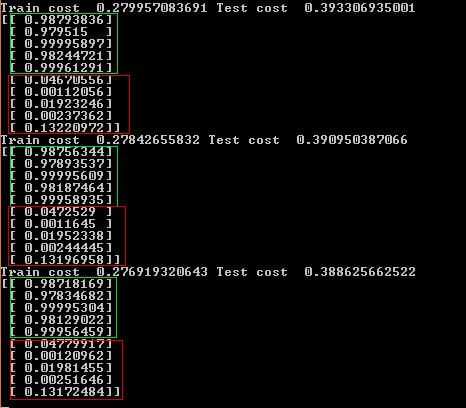
print('Train cost ', cost[0,0], 'Test cost ', costTest[0,0])
print(nt.runAll(nn, xTest))
After 400 iterations (approximately 1 min.), For some reason, the last test case had the highest error (output of the neural network 0.13), most likely in this case it would help to add training data to improve the quality.

In the cycle, we change theta in order to achieve the maximum result. It turns out that we are kind of slipping to the local minimum of the function (and if we added the gradient, we would go to the local maximum). The alf variable , often called the "learning speed", is responsible for how much we will change theta in each iteration. However, if you set the alpha parametertoo large, the network error may even increase or jump up and down since the function will simply step over the local minimum.
As you can see, the entire neural network consists of one variable of the dict type, so it is easy to serilize, and save it in a simple text file and restore it for future use.
Perhaps the next publication will be on the topic of how to speed up this code (and any other written in Python) using GPU computing
Full listing of the module, use as you wish
import copy
import numpy as np
import random as rd
import theano.tensor as th
class network:
# layers -list [5 10 10 5] - 5 input, 2 hidden
# layers (10 neurons each), 5 output
def create(self, layers):
theta = [0]
# for each layer from the first (skip zero layer!)
for i in range(1, len(layers)):
# create nxM+1 matrix (+bias!) with random floats in range [-1; 1]
theta.append(
np.mat(np.random.uniform(-1, 1, (layers[i], layers[i - 1] + 1))))
nn = {'theta': theta, 'structure': layers}
return nn
def runAll(self, nn, X):
z = [0]
m = len(X)
a = [copy.deepcopy(X)] # a[0] is equal to the first input values
logFunc = self.logisticFunctionVectorize()
# for each layer except the input
for i in range(1, len(nn['structure'])):
# add bias column to the previous matrix of activation functions
a[i - 1] = np.c_[np.ones(m), a[i - 1]]
# for all neurons in current layer multiply corresponds neurons
z.append(a[i - 1] * nn['theta'][i].T)
# in previous layers by the appropriate weights and sum the
# productions
a.append(logFunc(z[i])) # apply activation function for each value
nn['z'] = z
nn['a'] = a
return a[len(nn['structure']) - 1]
def run(self, nn, input):
z = [0]
a = []
a.append(copy.deepcopy(input))
a[0] = np.matrix(a[0]).T # nx1 vector
logFunc = self.logisticFunctionVectorize()
for i in range(1, len(nn['structure'])):
a[i - 1] = np.vstack(([1], a[i - 1]))
z.append(nn['theta'][i] * a[i - 1])
a.append(logFunc(z[i]))
nn['z'] = z
nn['a'] = a
return a[len(nn['structure']) - 1]
def logisticFunction(self, x):
a = 1 / (1 + np.exp(-x))
if a == 1:
a = 0.99999 # make smallest step to the direction of zero
elif a == 0:
a = 0.00001 # It is possible to use np.nextafter(0, 1) and
# make smallest step to the direction of one, but sometimes this step
# is too small and other algorithms fail :)
return a
def logisticFunctionVectorize(self):
return np.vectorize(self.logisticFunction)
def costTotal(self, theta, nn, X, y, lamb):
m = len(X)
# following string is for fmin_cg computaton
if type(theta) == np.ndarray:
nn['theta'] = self.roll(theta, nn['structure'])
y = np.matrix(copy.deepcopy(y))
# feed forward to obtain output of neural network
hAll = self.runAll(nn, X)
cost = self.cost(hAll, y)
# apply regularization
return cost / m + (lamb / (2 * m)) * self.regul(nn['theta'])
def cost(self, h, y):
logH = np.log(h)
log1H = np.log(1 - h)
# transpose y for matrix multiplication
cost = -1 * y.T * logH - (1 - y.T) * log1H
# sum matrix of costs for each output neuron and input vector
return cost.sum(axis=0).sum(axis=1)
def regul(self, theta):
reg = 0
thetaLocal = copy.deepcopy(theta)
for i in range(1, len(thetaLocal)):
# delete bias connection
thetaLocal[i] = np.delete(thetaLocal[i], 0, 1)
# square the values because they can be negative
thetaLocal[i] = np.power(thetaLocal[i], 2)
# sum at first rows, than columns
reg += thetaLocal[i].sum(axis=0).sum(axis=1)
return reg
def backpropagation(self, theta, nn, X, y, lamb):
layersNumb = len(nn['structure'])
thetaDelta = [0] * (layersNumb)
m = len(X)
# calculate matrix of outpit values for all input vectors X
hLoc = copy.deepcopy(self.runAll(nn, X))
yLoc = np.matrix(y)
thetaLoc = copy.deepcopy(nn['theta'])
derFunct = np.vectorize(
lambda x: (1 / (1 + np.exp(-x))) * (1 - (1 / (1 + np.exp(-x)))))
zLoc = copy.deepcopy(nn['z'])
aLoc = copy.deepcopy(nn['a'])
for n in range(0, len(X)):
delta = [0] * (layersNumb + 1) # fill list with zeros
# calculate delta of error of output layer
delta[len(delta) - 1] = (hLoc[n].T - yLoc[n].T)
for i in range(layersNumb - 1, 0, -1):
# we can not calculate delta[0] because we don't have theta[0]
# (and even we don't need it)
if i > 1:
z = zLoc[i - 1][n]
# add one for correct matrix multiplication
z = np.c_[[[1]], z]
delta[i] = np.multiply(
thetaLoc[i].T * delta[i + 1], derFunct(z).T)
delta[i] = delta[i][1:]
thetaDelta[i] = thetaDelta[i] + delta[i + 1] * aLoc[i - 1][n]
for i in range(1, len(thetaDelta)):
thetaDelta[i] = thetaDelta[i] / m
thetaDelta[i][:, 1:] = thetaDelta[i][:, 1:] + \
thetaLoc[i][:, 1:] * (lamb / m) # regularization
if type(theta) == np.ndarray:
# to work also with fmin_cg
return np.asarray(self.unroll(thetaDelta)).reshape(-1)
return thetaDelta
# create 1d array form lists like theta
def unroll(self, arr):
for i in range(0, len(arr)):
arr[i] = np.matrix(arr[i])
if i == 0:
res = (arr[i]).ravel().T
else:
res = np.vstack((res, (arr[i]).ravel().T))
res.shape = (1, len(res))
return res
# roll back 1d array to list with matrices according to given structure
def roll(self, arr, structure):
rolled = [arr[0]]
shift = 1
for i in range(1, len(structure)):
temparr = copy.deepcopy(
arr[shift:shift + structure[i] * (structure[i - 1] + 1)])
temparr.shape = (structure[i], structure[i - 1] + 1)
rolled.append(np.matrix(temparr))
shift += structure[i] * (structure[i - 1] + 1)
return rolled
UPD
Thanks to everyone who pluses.
