Principle for analyzing heart rate variability in MATLAB
Greetings, Habr! In this publication I want to present my experience in implementing the human HRV analysis algorithm in MATLAB. The subject of HRV analysis has been given enough attention on Habré. (search by ECG) however, as it seemed to me, some points are poorly disclosed or not considered at all. This article does not pay much attention to the explanation of the HRV phenomenon and the theory of methods for its analysis. It is understood that the reader is prepared, and the main emphasis is on the use of MATLAB functions and procedures for the analysis.
HRV analysis is based on determining the sequence of ECR RR intervals, i.e. between two consecutive heart contractions. They also use the concept of NN-intervals (normal-to-normal), that is, only the intervals between normal contractions are taken into account here (the analysis does not take into account the intervals recorded in case of heart rhythm disturbance, as well as those resulting from external interference).

The upper graph of the figure illustrates the process of detecting the duration of RR intervals by ECG.
The patient after inspection receives cardiointervalogram (CIG), which is a set of RR-intervals (lower graph pattern, which are displayed one after the other. Here, the height of the pulse is equal to the length of the respective RR-interval in ms and the time of occurrence of the next pulse corresponds to the time of its detection.
In Currently, there are several methods for assessing HRV, among which there are three groups:
In this regard, various methods for the analysis of HRV use different qualitative and quantitative assessment criteria. Sometimes there is a contradiction in the interpretation of data obtained on the basis of different methods for assessing heart rate. Therefore, the relevant methods are the total assessment of HRV indicators. R. M. Baevsky proposed for a comprehensive assessment of heart rhythm an indicator of the activity of regulatory systems (PARS), which is calculated in points based on the above methods. Those. a qualitative analysis of HRV should be carried out by all three methods, and the obtained data are used to calculate the PARS indicator.
The initial data for the analysis is the recording of successive time instants of the appearance of the next R-wave. 5-minute recordings are more often used for analysis, although there are options for analyzing recordings of a different duration.
To construct a CIG, it is necessary to know not only the moments of the appearance of the R-wave on the ECG, but also the length of time between two adjacent R-waves. To calculate this duration, use the MATALAB diff function, which calculates the final differences.
Next, determine the possible RR intervals that are not normal (obtain NN intervals). To do this, first create a unit vector of flag values for each RR interval:
Now we replace the elements of the flags vector (flags) corresponding to “abnormal” RR-intervals with zeros. Moreover, it is necessary to identify abnormal intervals manually.
To do this, we construct the CIG of the signal under study using the stem function.

The figure shows a fragment of the construction with an abnormal (not related to the sinus rhythm) interval, which value cannot be taken into account in further calculations.
Such intervals are removed from the CIG, and the areas of their removal will be interpolated by a linear method according to the size of adjacent intervals. This approach allows you to create an NN sequence without disturbing the overall dynamics of the signal. However, it should be noted that the result of the analysis of the CIG will be satisfactory with the value of the false intervals of not more than 5-6.
To restore deleted intervals, we use the MATLAB function for one-dimensional table interpolation. Syntax:
RRinterp = interp1 (x, y, xi, '<method>').
In this case, we take x - the time of occurrence of neighbors to the false (or group of false) intervals, y - their duration, xi - time of occurrence of false intervals marked with flags, '<method>' - 'linear'. As a result, the RRinterp variable returns the duration of the interpolated intervals.

At the next step, it is necessary to obtain Fig. 3 uniformly sampled signal using the smooth interpolation method. To do this, it is recommended to use cubic splines interpolation. The recommended sample rate for uniform sampling is 4 Hz.
To conduct a frequency analysis of the processed RIGspline CIG signal, it is necessary to get rid of its constant component, i.e. remove a linear trend. This is achieved by subtracting the arithmetic mean of the RRspline signal from the samples.
RRdetrend = RRspline - mean (RRspline);
The result is shown in the figure.

To conduct a frequency analysis (calculation of the power spectral density), it is necessary to perform the discrete Fourier transform (DFT) procedure. In this case, spectral leakage and comb distortions should be minimized. To do this, apply the window weighing method. It is recommended to use the Tukey window with 25% smoothing.
And also implement the complement of zeros.
The result of calculating the PSD of the investigated CIG signal, calculated on the basis of the FFT algorithm, is shown in the figure.
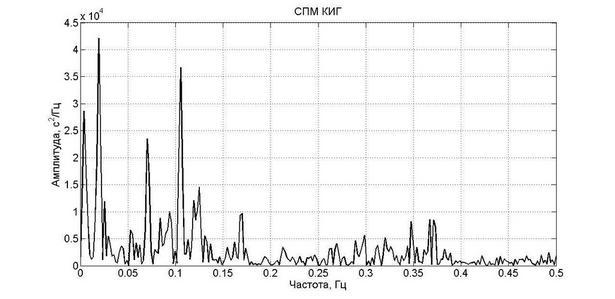
The periodogram method for using FFT is described here. In addition to it, there are the Welch method, autoregressive, etc.
According to the obtained data of the PSD, we calculate the power of the HF, LF, VLF signal components, as well as the total power of the TR. In accordance with the recommendations, the ranges will be limited to the following frequencies.
To calculate the power of the components, the trapz function is used. The function I = trapz (y) calculates the integral, assuming that the integration step is constant and equal to unity; in the case where the step h is different from unity but constant, multiply the calculated integral by h. In this case, h = (fInt / N), where fInt = 4 Hz is the sampling frequency, N is the number of calculated FFT bins.
The data obtained are sufficient to calculate the frequency parameters of PARS according to well-known formulas.
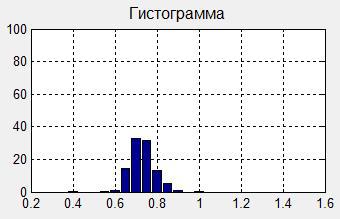
Define the geometric parameters of the histogram. To do this, in accordance with the recommendations, ranges of grouping of cardio-intervals are indicated and the hist command is used.
The result of the construction is shown in the figure.
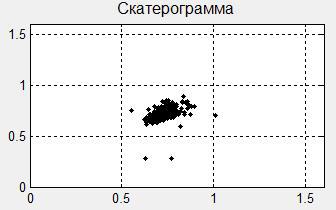
We are building a scatterogram.
PS: Since I am not a medical specialist, in terms I admit possible inaccuracies.
The described analysis principle appeared on the basis of the sources I found and the developments that were already made publicly available.
Due to the peculiarities of the genre, the material tried to be laconic, omitting some technical aspects of MATLAB.
I will be glad to constructive criticism and try to answer possible questions. I hope the material will be useful to someone. Thanks for attention!
The basic about research methods is sufficiently accessible and basic
Baevsky R.M. et al. Analysis of heart rate variability using various electrocardiographic systems
Measurement standards and recommendations for HRV analysis
PhysioNet RR-interval records database
Ready-to-use MATLAB functions: Software for Heart Rate Variability
HRV analysis is based on determining the sequence of ECR RR intervals, i.e. between two consecutive heart contractions. They also use the concept of NN-intervals (normal-to-normal), that is, only the intervals between normal contractions are taken into account here (the analysis does not take into account the intervals recorded in case of heart rhythm disturbance, as well as those resulting from external interference).

The upper graph of the figure illustrates the process of detecting the duration of RR intervals by ECG.
The patient after inspection receives cardiointervalogram (CIG), which is a set of RR-intervals (lower graph pattern, which are displayed one after the other. Here, the height of the pulse is equal to the length of the respective RR-interval in ms and the time of occurrence of the next pulse corresponds to the time of its detection.
In Currently, there are several methods for assessing HRV, among which there are three groups:
- time domain methods - rely on statistical methods and are aimed at the study of general variability;
- autocorrelation analysis and correlation rhythmography - integral indicators of HRV;
- frequency domain methods - the study of the periodic components of HRV.
In this regard, various methods for the analysis of HRV use different qualitative and quantitative assessment criteria. Sometimes there is a contradiction in the interpretation of data obtained on the basis of different methods for assessing heart rate. Therefore, the relevant methods are the total assessment of HRV indicators. R. M. Baevsky proposed for a comprehensive assessment of heart rhythm an indicator of the activity of regulatory systems (PARS), which is calculated in points based on the above methods. Those. a qualitative analysis of HRV should be carried out by all three methods, and the obtained data are used to calculate the PARS indicator.
The initial data for the analysis is the recording of successive time instants of the appearance of the next R-wave. 5-minute recordings are more often used for analysis, although there are options for analyzing recordings of a different duration.
To construct a CIG, it is necessary to know not only the moments of the appearance of the R-wave on the ECG, but also the length of time between two adjacent R-waves. To calculate this duration, use the MATALAB diff function, which calculates the final differences.
RR = diff(D_times); % Расчет RR-интервалов. Здесь D_times – моменты времени детектирования R-зубца, загруженные из файла данных
times = D_times(2:(length(D_times))); % Итоговый вектор временных отметок.
Next, determine the possible RR intervals that are not normal (obtain NN intervals). To do this, first create a unit vector of flag values for each RR interval:
flags = ones(max(size(RR)),1); % Вектор флагов нормальных RR-интервалов.
Now we replace the elements of the flags vector (flags) corresponding to “abnormal” RR-intervals with zeros. Moreover, it is necessary to identify abnormal intervals manually.
To do this, we construct the CIG of the signal under study using the stem function.
stem (RR, 'Marker','.', 'color', [0 0 0]),
title ('Уточнение синусового ритма', 'FontSize', 12);
xlabel('Номер интервала','FontSize',12);
ylabel('Длительность, сек.','FontSize',12);

The figure shows a fragment of the construction with an abnormal (not related to the sinus rhythm) interval, which value cannot be taken into account in further calculations.
Such intervals are removed from the CIG, and the areas of their removal will be interpolated by a linear method according to the size of adjacent intervals. This approach allows you to create an NN sequence without disturbing the overall dynamics of the signal. However, it should be noted that the result of the analysis of the CIG will be satisfactory with the value of the false intervals of not more than 5-6.
To restore deleted intervals, we use the MATLAB function for one-dimensional table interpolation. Syntax:
RRinterp = interp1 (x, y, xi, '<method>').
In this case, we take x - the time of occurrence of neighbors to the false (or group of false) intervals, y - their duration, xi - time of occurrence of false intervals marked with flags, '<method>' - 'linear'. As a result, the RRinterp variable returns the duration of the interpolated intervals.

At the next step, it is necessary to obtain Fig. 3 uniformly sampled signal using the smooth interpolation method. To do this, it is recommended to use cubic splines interpolation. The recommended sample rate for uniform sampling is 4 Hz.
fInt = 4; % Частота дискретизации интерполированного сигнала/
xSpline = min(times): 1/fInt: max(times); % Сетка интерполяции/
RRspline = interp1(times, RRint, xSpline, 'spline'); % Интерполяция кубическими сплайнами. times – время появления интервалов, RRint – длительность полученных NN-интервалов.
To conduct a frequency analysis of the processed RIGspline CIG signal, it is necessary to get rid of its constant component, i.e. remove a linear trend. This is achieved by subtracting the arithmetic mean of the RRspline signal from the samples.
RRdetrend = RRspline - mean (RRspline);
The result is shown in the figure.

To conduct a frequency analysis (calculation of the power spectral density), it is necessary to perform the discrete Fourier transform (DFT) procedure. In this case, spectral leakage and comb distortions should be minimized. To do this, apply the window weighing method. It is recommended to use the Tukey window with 25% smoothing.
w = tukeywin(length(rrdetrend), 0.25); % Окно Тьюки с 25% косинусоидальными фронтами.
rrdetrend = (w'.*rrdetrend).*1000; % Умножение сигнала на оконную функцию для устранения растекания спектра и получение сигнала в мс.
And also implement the complement of zeros.
Pspectr = fft(rrdetrend, 2048); % БПФ дополненное нулями до 2^11.
The result of calculating the PSD of the investigated CIG signal, calculated on the basis of the FFT algorithm, is shown in the figure.

The periodogram method for using FFT is described here. In addition to it, there are the Welch method, autoregressive, etc.
According to the obtained data of the PSD, we calculate the power of the HF, LF, VLF signal components, as well as the total power of the TR. In accordance with the recommendations, the ranges will be limited to the following frequencies.
BW = [0.003 0.04; ... % Гц, VLF
0.04 0.15; ... % Гц, LF
0.15 0.4]; % Гц, HF
To calculate the power of the components, the trapz function is used. The function I = trapz (y) calculates the integral, assuming that the integration step is constant and equal to unity; in the case where the step h is different from unity but constant, multiply the calculated integral by h. In this case, h = (fInt / N), where fInt = 4 Hz is the sampling frequency, N is the number of calculated FFT bins.
The data obtained are sufficient to calculate the frequency parameters of PARS according to well-known formulas.
Define the geometric parameters of the histogram. To do this, in accordance with the recommendations, ranges of grouping of cardio-intervals are indicated and the hist command is used.
dRR = 0.4: 0.05: 1.3; % Диапазоны группировки кардиоинтервалов
[ampRR, dRR] = hist (RRspline, dRR); % Расчет гистограммы
ampRR_proc = (ampRR.*100)./length(rrspline); % Получение данных в процентах
[yMo, yi] = max (ampRR);
Mo = dRR(yi); % Мода - наиболее часто встречающееся значение кардиоинтервала
AMo = (yMo*100)/length(RRspline); % Амплитуда моды
MxDMn = (max(RRspline) - min(RRspline)); % Вариационный размах
bar (dRR, ampRR_proc), grid on % Построение гистограммы.
title ('Гистограмма', 'FontSize', 12);
ylabel('%','FontSize',12);
axis ([0.2 1.6 0 100])
The result of the construction is shown in the figure.

We are building a scatterogram.
rr1 = RRspline (1 : 2:end); % Абсцисса (х) RR(n)
rr2 = RRspline (2 : 2: end); % Ордината (у) RR(n+1)
if length(rr1) ~= length(rr2)
if length(rr1) > length(rr2)
rr1 = rr1 (1: end - 1);
else rr2 = rr2 (1: end - 1);
end
end
plot (rr1, rr2,'Marker','.','LineStyle','none','Color',[0 0 0])
title ('Скатерограмма', 'FontSize', 12), grid on
axis ([0 1.6 0 1.6])

PS: Since I am not a medical specialist, in terms I admit possible inaccuracies.
The described analysis principle appeared on the basis of the sources I found and the developments that were already made publicly available.
Due to the peculiarities of the genre, the material tried to be laconic, omitting some technical aspects of MATLAB.
I will be glad to constructive criticism and try to answer possible questions. I hope the material will be useful to someone. Thanks for attention!
Sources
The basic about research methods is sufficiently accessible and basic
Baevsky R.M. et al. Analysis of heart rate variability using various electrocardiographic systems
Measurement standards and recommendations for HRV analysis
PhysioNet RR-interval records database
Ready-to-use MATLAB functions: Software for Heart Rate Variability
