Fast factorial algorithms
The concept of factorial is known to all. This is a function that calculates the product of consecutive natural numbers from 1 to N inclusive: N! = 1 * 2 * 3 * ... * N. Factorial is a fast-growing function, already for small values of N the value N! has many significant numbers.
Let's try to implement this function in a programming language. Obviously, we need a language that supports long arithmetic. I will use C #, but with the same success you can take Java or Python.
The naive algorithm
So, the simplest implementation (let's call it naive) is obtained directly from the definition of factorial:
On my machine, this implementation works for about 1.6 seconds for N = 50,000.
Next, we consider algorithms that work much faster than a naive implementation.
Tree Computing Algorithm
The first algorithm is based on the consideration that long numbers of approximately the same length are more effective to multiply than a long number to multiply by a short one (as in a naive implementation). That is, we need to ensure that when calculating the factorial, the factors are constantly approximately the same length.
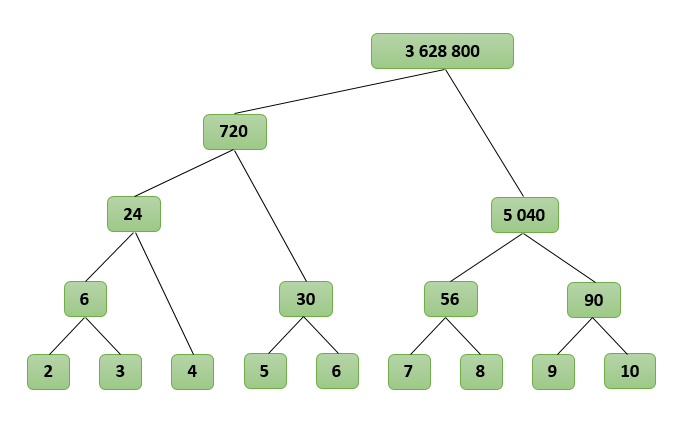
Suppose we need to find the product of consecutive numbers from L to R, we denote it as P (L, R). Divide the interval from L to R in half and calculate P (L, R) as P (L, M) * P (M + 1, R), where M is in the middle between L and R, M = (L + R) / 2 . Note that the factors will be approximately the same length. We similarly divide P (L, M) and P (M + 1, R). We will perform this operation until no more than two factors remain in each interval. Obviously, P (L, R) = L if L and R are equal, and P (L, R) = L * R if L and R differ by one. To find N! you need to count P (2, N).
Let's see how our algorithm works for N = 10, we find P (2, 10):
P (2, 10)
P (2, 6) * P (7, 10)
(P (2, 4) * P (5 , 6)) * (P (7, 8) * P (9, 10))
((P (2, 3) * P (4)) * P (5, 6)) * (P (7, 8) * P (9, 10))
(((2 * 3) * (4)) * (5 * 6)) * ((7 * 8) * (9 * 10))
((6 * 4) * 30) * (56 * 90)
(24 * 30) * (5 040)
720 * 5 040
3 628 800
It turns out a kind of tree where the factors are in the nodes, and the result is in the root We
implement the described algorithm:
For N = 50,000, factorial is calculated in 0.9 seconds, which is almost twice as fast as in a naive implementation.
Factorization Calculation Algorithm The
second fast calculation algorithm uses factorization into prime factors (factorization). Obviously, in the decomposition N! only prime factors from 2 to N are involved. Let's try to calculate how many times the prime factor K is contained in N !, that is, find out the degree of the factor K in the expansion. Each K-th term of the product 1 * 2 * 3 * ... * N increases the exponent by one, that is, the exponent will be equal to N / K. But each K- second term increases the exponent by one more, that is, the exponent becomes N / K + N / K 2 . Similarly for K 3 , K 4etc. As a result, we get that the exponent with a simple factor K will be N / K + N / K 2 + N / K 3 + N / K 4 + ...
For clarity, we calculate how many times the deuce is 10 times! Every second factor gives (2, 4, 6, 8, and 10), a total of 10/2 = 5 such factors. Every fourth gives a quadruple (2 2 ), all these factors are 10/4 = 2 (4 and 8). Every eighth gives a figure of eight (2 3 ), such a factor of only one 10/8 = 1 (8). Sixteen (2 4 ) and more does not give a single factor, which means that the calculation can be completed. Summing up, we get that the exponent for a deuce in the expansion of 10! by prime factors it will be equal to 10/2 + 10/4 + 10/8 = 5 + 2 + 1 = 8.
If you act in the same way, you can find the indicators at 3, 5 and 7 in the expansion 10!, After which it remains only to calculate the value of the product:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800 It
remains to find primes from 2 to N, for this you can use the sieve of Eratosthenes :
This implementation also takes about 0.9 seconds to calculate 50,000!
GMP library
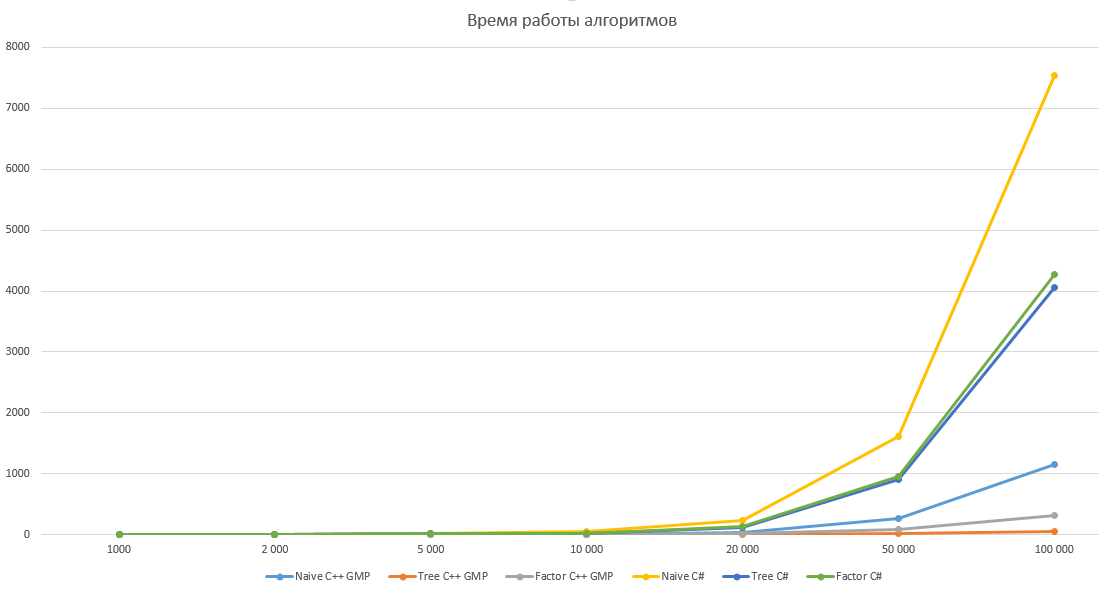
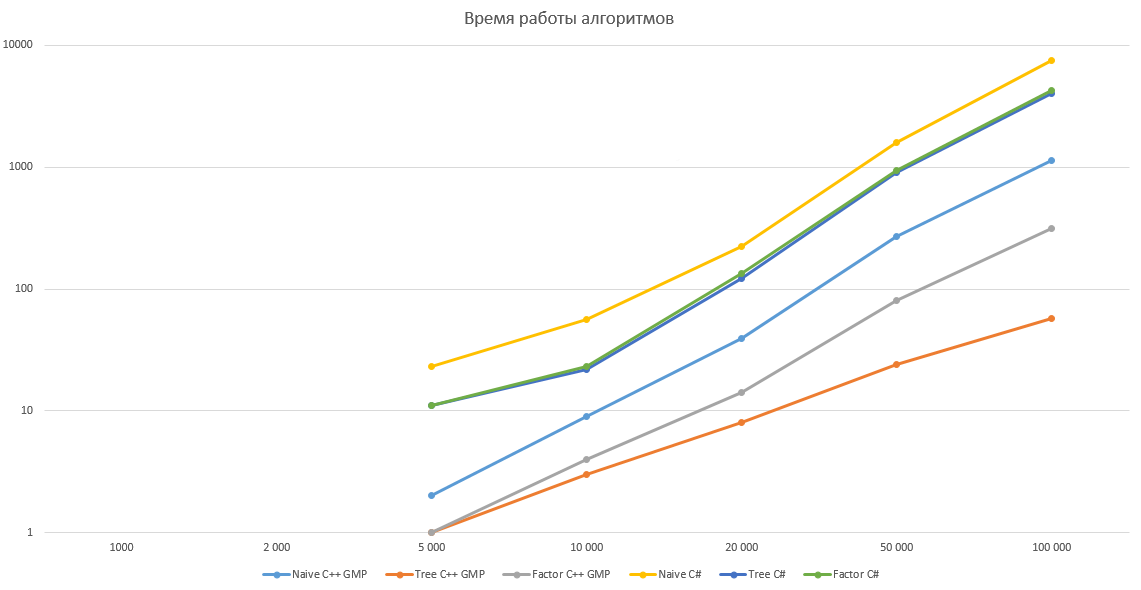
As pomme rightly noted , factorial computation speed is 98% dependent on the rate of multiplication. Let's try to test our algorithms by implementing them in C ++ using the GMP library . The test results are given below, it turns out that the multiplication algorithm in C # has rather strange asymptotics, therefore optimization gives a relatively small gain in C # and huge in C ++ with GMP. However, this issue is probably worth a separate article.
Performance comparison
All algorithms were tested for N equal to 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 in ten iterations. The table shows the average operating time in milliseconds.

Graph with a linear scale
Graph with a logarithmic scale
Ideas and algorithms from comments The
guards offered a lot of interesting ideas and algorithms in response to my article, here I will leave links to the best of them
lany parallelized the tree in Java using the Stream API and got 18 times
acceleration Mrrl suggested factorization optimization by 15-20%
PsyHaSTe suggested an improvement in a naive implementation
Krypt suggested a parallel version in C #
SemenovVV suggested an implementation on Go
pomme suggested using GMP
ShashkovS suggested a fast algorithm in Python
Source codes
The source codes of the implemented algorithms are given under spoilers
Let's try to implement this function in a programming language. Obviously, we need a language that supports long arithmetic. I will use C #, but with the same success you can take Java or Python.
The naive algorithm
So, the simplest implementation (let's call it naive) is obtained directly from the definition of factorial:
static BigInteger FactNaive(int n)
{
BigInteger r = 1;
for (int i = 2; i <= n; ++i)
r *= i;
return r;
}
On my machine, this implementation works for about 1.6 seconds for N = 50,000.
Next, we consider algorithms that work much faster than a naive implementation.
Tree Computing Algorithm
The first algorithm is based on the consideration that long numbers of approximately the same length are more effective to multiply than a long number to multiply by a short one (as in a naive implementation). That is, we need to ensure that when calculating the factorial, the factors are constantly approximately the same length.
Suppose we need to find the product of consecutive numbers from L to R, we denote it as P (L, R). Divide the interval from L to R in half and calculate P (L, R) as P (L, M) * P (M + 1, R), where M is in the middle between L and R, M = (L + R) / 2 . Note that the factors will be approximately the same length. We similarly divide P (L, M) and P (M + 1, R). We will perform this operation until no more than two factors remain in each interval. Obviously, P (L, R) = L if L and R are equal, and P (L, R) = L * R if L and R differ by one. To find N! you need to count P (2, N).
Let's see how our algorithm works for N = 10, we find P (2, 10):
P (2, 10)
P (2, 6) * P (7, 10)
(P (2, 4) * P (5 , 6)) * (P (7, 8) * P (9, 10))
((P (2, 3) * P (4)) * P (5, 6)) * (P (7, 8) * P (9, 10))
(((2 * 3) * (4)) * (5 * 6)) * ((7 * 8) * (9 * 10))
((6 * 4) * 30) * (56 * 90)
(24 * 30) * (5 040)
720 * 5 040
3 628 800
It turns out a kind of tree where the factors are in the nodes, and the result is in the root We

implement the described algorithm:
static BigInteger ProdTree(int l, int r)
{
if (l > r)
return 1;
if (l == r)
return l;
if (r - l == 1)
return (BigInteger)l * r;
int m = (l + r) / 2;
return ProdTree(l, m) * ProdTree(m + 1, r);
}
static BigInteger FactTree(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
return ProdTree(2, n);
}
For N = 50,000, factorial is calculated in 0.9 seconds, which is almost twice as fast as in a naive implementation.
Factorization Calculation Algorithm The
second fast calculation algorithm uses factorization into prime factors (factorization). Obviously, in the decomposition N! only prime factors from 2 to N are involved. Let's try to calculate how many times the prime factor K is contained in N !, that is, find out the degree of the factor K in the expansion. Each K-th term of the product 1 * 2 * 3 * ... * N increases the exponent by one, that is, the exponent will be equal to N / K. But each K- second term increases the exponent by one more, that is, the exponent becomes N / K + N / K 2 . Similarly for K 3 , K 4etc. As a result, we get that the exponent with a simple factor K will be N / K + N / K 2 + N / K 3 + N / K 4 + ...
For clarity, we calculate how many times the deuce is 10 times! Every second factor gives (2, 4, 6, 8, and 10), a total of 10/2 = 5 such factors. Every fourth gives a quadruple (2 2 ), all these factors are 10/4 = 2 (4 and 8). Every eighth gives a figure of eight (2 3 ), such a factor of only one 10/8 = 1 (8). Sixteen (2 4 ) and more does not give a single factor, which means that the calculation can be completed. Summing up, we get that the exponent for a deuce in the expansion of 10! by prime factors it will be equal to 10/2 + 10/4 + 10/8 = 5 + 2 + 1 = 8.
If you act in the same way, you can find the indicators at 3, 5 and 7 in the expansion 10!, After which it remains only to calculate the value of the product:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800 It
remains to find primes from 2 to N, for this you can use the sieve of Eratosthenes :
static BigInteger FactFactor(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
bool[] u = new bool[n + 1]; // маркеры для решета Эратосфена
List> p = new List>(); // множители и их показатели степеней
for (int i = 2; i <= n; ++i)
if (!u[i]) // если i - очередное простое число
{
// считаем показатель степени в разложении
int k = n / i;
int c = 0;
while (k > 0)
{
c += k;
k /= i;
}
// запоминаем множитель и его показатель степени
p.Add(new Tuple(i, c));
// просеиваем составные числа через решето
int j = 2;
while (i * j <= n)
{
u[i * j] = true;
++j;
}
}
// вычисляем факториал
BigInteger r = 1;
for (int i = p.Count() - 1; i >= 0; --i)
r *= BigInteger.Pow(p[i].Item1, p[i].Item2);
return r;
}
This implementation also takes about 0.9 seconds to calculate 50,000!
GMP library
As pomme rightly noted , factorial computation speed is 98% dependent on the rate of multiplication. Let's try to test our algorithms by implementing them in C ++ using the GMP library . The test results are given below, it turns out that the multiplication algorithm in C # has rather strange asymptotics, therefore optimization gives a relatively small gain in C # and huge in C ++ with GMP. However, this issue is probably worth a separate article.
Performance comparison
All algorithms were tested for N equal to 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 in ten iterations. The table shows the average operating time in milliseconds.

Graph with a linear scale

Graph with a logarithmic scale

Ideas and algorithms from comments The
guards offered a lot of interesting ideas and algorithms in response to my article, here I will leave links to the best of them
lany parallelized the tree in Java using the Stream API and got 18 times
acceleration Mrrl suggested factorization optimization by 15-20%
PsyHaSTe suggested an improvement in a naive implementation
Krypt suggested a parallel version in C #
SemenovVV suggested an implementation on Go
pomme suggested using GMP
ShashkovS suggested a fast algorithm in Python
Source codes
The source codes of the implemented algorithms are given under spoilers
C #
using System;
using System.Linq;
using System.Text;
using System.Numerics;
using System.Collections.Generic;
using System.Collections.Specialized;
namespace BigInt
{
class Program
{
static BigInteger FactNaive(int n)
{
BigInteger r = 1;
for (int i = 2; i <= n; ++i)
r *= i;
return r;
}
static BigInteger ProdTree(int l, int r)
{
if (l > r)
return 1;
if (l == r)
return l;
if (r - l == 1)
return (BigInteger)l * r;
int m = (l + r) / 2;
return ProdTree(l, m) * ProdTree(m + 1, r);
}
static BigInteger FactTree(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
return ProdTree(2, n);
}
static BigInteger FactFactor(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
bool[] u = new bool[n + 1];
List> p = new List>();
for (int i = 2; i <= n; ++i)
if (!u[i])
{
int k = n / i;
int c = 0;
while (k > 0)
{
c += k;
k /= i;
}
p.Add(new Tuple(i, c));
int j = 2;
while (i * j <= n)
{
u[i * j] = true;
++j;
}
}
BigInteger r = 1;
for (int i = p.Count() - 1; i >= 0; --i)
r *= BigInteger.Pow(p[i].Item1, p[i].Item2);
return r;
}
static void Main(string[] args)
{
int n;
int t;
Console.Write("n = ");
n = Convert.ToInt32(Console.ReadLine());
t = Environment.TickCount;
BigInteger fn = FactNaive(n);
Console.WriteLine("Naive time: {0} ms", Environment.TickCount - t);
t = Environment.TickCount;
BigInteger ft = FactTree(n);
Console.WriteLine("Tree time: {0} ms", Environment.TickCount - t);
t = Environment.TickCount;
BigInteger ff = FactFactor(n);
Console.WriteLine("Factor time: {0} ms", Environment.TickCount - t);
Console.WriteLine("Check: {0}", fn == ft && ft == ff ? "ok" : "fail");
}
}
}
C ++ with GMP
#include
#include
#include
#include
#include
using namespace std;
mpz_class FactNaive(int n)
{
mpz_class r = 1;
for (int i = 2; i <= n; ++i)
r *= i;
return r;
}
mpz_class ProdTree(int l, int r)
{
if (l > r)
return 1;
if (l == r)
return l;
if (r - l == 1)
return (mpz_class)r * l;
int m = (l + r) / 2;
return ProdTree(l, m) * ProdTree(m + 1, r);
}
mpz_class FactTree(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
return ProdTree(2, n);
}
mpz_class FactFactor(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
vector u(n + 1, false);
vector > p;
for (int i = 2; i <= n; ++i)
if (!u[i])
{
int k = n / i;
int c = 0;
while (k > 0)
{
c += k;
k /= i;
}
p.push_back(make_pair(i, c));
int j = 2;
while (i * j <= n)
{
u[i * j] = true;
++j;
}
}
mpz_class r = 1;
for (int i = p.size() - 1; i >= 0; --i)
{
mpz_class w;
mpz_pow_ui(w.get_mpz_t(), mpz_class(p[i].first).get_mpz_t(), p[i].second);
r *= w;
}
return r;
}
mpz_class FactNative(int n)
{
mpz_class r;
mpz_fac_ui(r.get_mpz_t(), n);
return r;
}
int main()
{
int n;
unsigned int t;
cout << "n = ";
cin >> n;
t = clock();
mpz_class fn = FactNaive(n);
cout << "Naive: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
t = clock();
mpz_class ft = FactTree(n);
cout << "Tree: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
t = clock();
mpz_class ff = FactFactor(n);
cout << "Factor: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
t = clock();
mpz_class fz = FactNative(n);
cout << "Native: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
cout << "Check: " << (fn == ft && ft == ff && ff == fz ? "ok" : "fail") << endl;
return 0;
}
