Description of digital vending machines on VHDL
- Tutorial
Bit of theory
Цифровой автомат (ЦА) — это устройство, которое осуществляет прием, хранение и преобразование дискретной информации по некоторому алгоритму и может находиться в одном из нескольких устойчивых состояний [7].
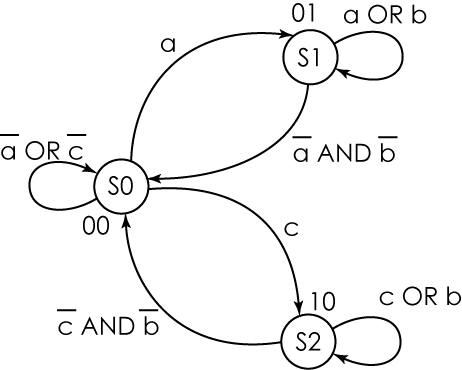
Рисунок 1 — Граф цифрового автомата
Если выходной сигнал цифрового автомата зависит лишь от текущего состояния, то такой автомат называется автоматом Мура, если же выходной сигнал зависит от текущего состояния и входных сигналов, то такой цифровой автомат носит название автомата Мили.
Цифровой автомат может быть описан с помощью таких представлений:
— в виде ориентированного графа,
— с помощью переходов и выходов.
The representation of a digital automaton in the form of a directed graph is shown in Fig. 1. Here, in circles — vertices of the graph — the states of the digital automaton are shown, transitions between states are shown by arcs between vertices, and transition to the same state is shown by a loop.
Near arcs and loops, the values of the input signals at which this transition occurs are shown. For example, (a OR b) means that this transition will occur when a = 1 or b = 1 .
The output signals for the Moore automaton are shown near the vertices of the graph, and for the digital Mily automaton, they are shown on arcs near the input signals. T.O. in fig. 1 shows a digital Moore machine.
Representation of a digital automaton using tables assumes the presence of two tables: transition tables and exit tables.The transition table links together the current state, input signals and the future state of the digital machine. The transition table of the CA described by the graph in Fig. 1 is shown in table. 1.
Table 1 - Transition table of the digital machine
| Current state | Next state | Transition Condition |
| S0 | S0 | a = 0 OR c = 0 |
| S0 | S1 | a = 1 |
| S1 | S1 | a = 1 OR b = 1 |
| S1 | S0 | a = 0 and b = 0 |
| S0 | S2 | c = 1 |
| S2 | S2 | c = 1 OR b = 1 |
| S2 | S0 | c = 0 and b = 0 |
Output table - shows the correspondence of the current state of the digital machine and its output signals (Table 2).
Table 2 - the table of the outputs of the digital machine}
| Current state | Exit |
| S0 | 00 |
| S1 | 01 |
| S2 | 10 |
When implementing a digital machine, we will adhere to the principle of separation into the combinational and sequential parts of the circuit. With this interpretation, a digital machine will be represented by three blocks (Figure 2):
- a combination block of transition logic;
- a register for storing CA states;
- a combination block for generating output signals - different for the TsA Miles and Moore.

Figure 2 - Schematic
diagram of a digital machine with asynchronous outputs The logic diagram of the transitions to its input receives the current state code of the digital machine ( present_st ) and external signals ( input_signal ). The output of this block will be the next state code ( next_st ).
INThe state register includes three signals: clock ( clk ), reset ( reset ) and the next state code ( next_st ). The clock and reset signals are designed to control triggers that store the state of the digital machine. On the rising edge of the clock signal, the next state ( next_st ) is recorded in the triggers. The results of writing to triggers appear at the output of the status register as a signal of the current state of the CA ( present_st ).
Output Signal Generatordepending on the state of the CA (and the input signals for the Miles machine) generates asynchronous output signals. To obtain synchronous output signals, a register is additionally built into this unit.
Using VHDL to describe digital machines
To describe the states of a digital machine, an enumerated type must be used. For this, a type ( state_type ) is described , the values of which are the states of the digital machine. Then the signal ( state ) of this enumerated type is described , in which the current state of the automaton will be stored.
TYPE state_type IS (init, state1, state2, ...);
SIGNAL state: state_type;
Upon implementation, a scheme of several triggers will be obtained. Depending on the state encoding method, the number of triggers may vary, which affects the speed and size of the circuit. We'll talk more about encoding methods a bit later.
To describe the operation of the digital automaton and to create combinational circuits of the logic of transitions and outputs, it is necessary to use the corresponding tables and use the case operator to analyze the values of the present_st signal .
The process that describes the combination part for calculating the transition logic of a digital automaton can be described using this template:
PROCESS (present_st, input_signal)
BEGIN
CASE present_st IS
WHEN state1 =>
IF input_signal = '1'
THEN next_st <= state1;
ELSE next_st <= state2;
END IF;
WHEN state2 =>
IF input_signal = '1'
THEN next_st <= state2;
ELSE next_st <= state3;
END IF;
...
END CASE;
END PROCESS;
To describe the logic of the output signals, it is possible to use a process operator or a parallel conditional assignment operator.
The process that describes the combination part for calculating the outputs of a digital Moore automaton can be described using this template:
PROCESS (present_st)
BEGIN
CASE present_st IS
WHEN state1 =>
output <= "000";
WHEN state2 =>
output <= "001";
...
END CASE;
END PROCESS;
Here, in the process initialization list, only the current state of the present_st digital machine is used , the values of which are analyzed using the case operator .
For the Miles machine, the same process will look like this:
PROCESS (present_st, input_signal)
BEGIN
CASE present_st IS
WHEN state1 =>
IF input_signal = '1'
THEN output <= "000";
ELSE output <= "001";
END IF;
WHEN state2 =>
IF input_signal = '1'
THEN output <= "011";
ELSE OUTPUT <= "010";
END IF;
...
END CASE;
END PROCESS;
This process uses the current CA state ( present_st ) and the input signal ( input_signal ) for initialization, since changes to any of these signals should trigger the process.
To obtain synchronous output signals, it is necessary to use a process with only the clock signal clk in the initialization list . Analysis of the current state as in the previous case is performed using the case statement .
PROCESS (clk)
BEGIN
IF (rising_edge(clk)) THEN
CASE present_st IS
WHEN state1 =>
output <= "000";
WHEN state2 =>
output <= "001";
...
END CASE;
END IF;
END PROCESS;
Generating output signals using parallel conditional assignment does not require a process operator. In this case, you can use the following construction:
output <= "000" WHEN present_st = state1 ELSE
"001" WHEN present_st = state2 ELSE
...
"100";
При описании последовательностной части цифрового автомата в списке инициализаторов процесса должны содержатся сигналы clk и reset. При поступлении сигнала сброса reset цифровой автомат переходит в начальное состояние init, из которого начинается работа всего автомата. Передний фронт сигнала clk приводит к записи в триггеры ЦА его нового текущего состояния, т.е. сигнал next_st переписывается в сигнал present_st.
Фактически последовательностная часть представляет собой регистр со сбросом:
PROCESS (clk, reset)
BEGIN
IF reset = '1'
THEN present_st <= Init;
ELSIF (rising_edge(clk))
THEN present_st <= next_st;
END IF;
END PROCESS;
The reset signal may be synchronous or asynchronous. The listing above describes an asynchronous reset option.
When using an asynchronous reset signal, we always know in what state the digital machine will be when the power is turned on, i.e. before a clock signal arrives and the system starts functioning normally. In this case, there is no need to decode the unused states of the digital automaton, which reduces the logic of transitions.
Using a synchronous reset signal does not allow you to determine what state the machine will be at power on. It is possible that he will “stick” in one of the undescribed states. T.O. when describing a digital automaton, it is necessary to describe all 2 ^ n combinations of trigger states, regardless of whether they are operating states of a digital automaton or not. Here n is the number of triggers used to encode the digital machine. This, in turn, will lead to an increase in the transition logic scheme.
In order to avoid the “sticking” of the target audience in undescribed states, it is necessary to explicitly register actions in such situations using the when ... others construct . For example, it is possible to use such a process to describe synchronous reset and actions in unused states.
PROCESS (clk)
BEGIN
IF (rising_edge(clk)) THEN
IF reset = '1'
THEN state <= init;
ELSE
CASE state IS
WHEN state1 =>
IF input_signal = '1'
THEN state <= state1;
ELSE
state <= state2;
END IF;
WHEN state2 =>
IF input_signal = '1'
THEN state <= state2;
ELSE
state <= state3;
END IF;
...
WHEN OTHERS =>
state <= init;
END CASE;
END IF;
END IF;
END PROCESS;
Three two one
A digital machine can be described using one, two, or three process operators. We will consider these options using the example of a digital traffic light control machine.
This digital machine has five states: initial (Init), red (R), green (G) and two yellow ones - one for switching from red to green (RG), and the second from green to red (GR). In the case when the input cnt is equal to zero, no transitions occur, when the input cnt is equal to one, a transition to the next state occurs. The graph of the digital automaton is shown in Fig. 3.
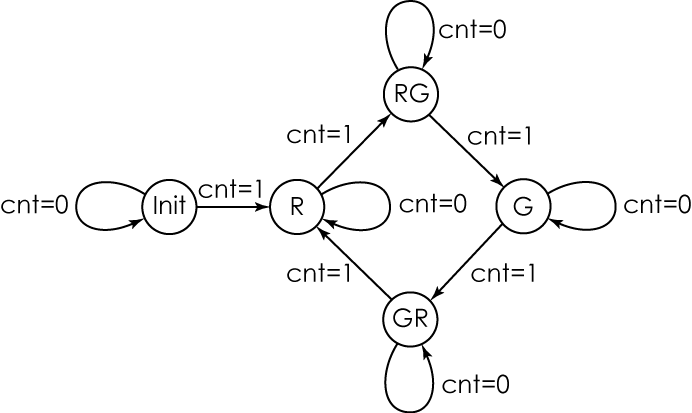
Figure 3 - Graph of a digital traffic light
The same machine can be represented using the transition table and the output table. The output signal is represented by a three-bit vector, in which the most significant bit is responsible for red, the second for yellow and the least for green.
Table 3 - conversion table
| present_ st | next_st | Transition Condition |
| Init | Init | cnt = 0 |
| Init | R | cnt = 1 |
| R | R | cnt = 0 |
| R | Rg | cnt = 1 |
| Rg | Rg | cnt = 0 |
| Rg | G | cnt = 1 |
| G | G | cnt = 0 |
| G | GR | cnt = 1 |
| GR | GR | cnt = 0 |
| GR | R | cnt = 1 |
Table 4 - Output Table
| present_st | output |
| Init | 000 |
| R | 100 |
| Rg | 010 |
| G | 001 |
| GR | 010 |
To describe the states of CA, it is necessary to describe an enumerated type in which all states will be listed. In the above example, the state_type type is introduced , which contains five values: Init, R, RG, G, GR . For the operation of a specific instance of a digital machine, it is necessary to describe signals of this type. In the example, these are signals next_st, present_s t for storing the subsequent and current states of the automaton, respectively. When performing processes, this signal will take on the value of the current state of the digital machine.
Now we will consider the description of this digital automaton using three processes (Figure 4), each of which describes a separate part of the digital automaton:
- the combination part for the transition logic;
- combination part for output signals;
- the serial part is only for recording the states of the digital automaton.
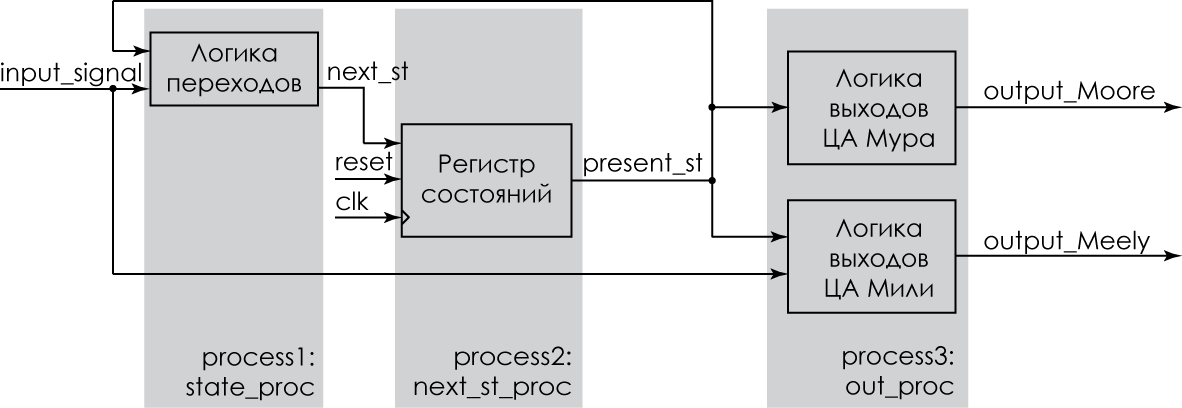
Figure 4 - Digital machine with three processes
This option for describing a digital machine allows the developer to separate the transition logic from the logic for generating the output signals and synchronously record the state of the machine in the state storage register. And this, in turn, makes it easier to describe and debug a synchronous digital machine.
The program itself is a combination of the three processes described above.
Description of a digital machine using three processes
LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
ENTITY traffic IS
PORT(clk : IN std_logic;
cnt : IN std_logic;
reset : IN std_logic;
output : OUT std_logic_vector(2 downto 0)
);
END ENTITY;
ARCHITECTURE rtl OF traffic IS
TYPE state_type IS (Init, R, RG, G, GR);
SIGNAL next_st, present_st: state_type;
BEGIN
state_proc:
PROCESS (present_st, cnt)
BEGIN
CASE present_st IS
WHEN Init =>
IF cnt = '1'
THEN next_st <= R;
ELSE
next_st <= Init;
END IF;
WHEN R =>
if cnt = '1'
THEN next_st <= RG;
ELSE
next_st <= R;
END IF;
WHEN RG =>
IF cnt = '1'
THEN next_st <= G;
ELSE
next_st <= RG;
END IF;
WHEN G =>
IF cnt = '1'
THEN NEXT_st <= GR;
ELSE
next_st <= G;
END IF;
WHEN GR =>
IF CNT = '1'
THEN next_st <= R;
ELSE
next_st <= GR;
END IF;
WHEN OTHERS =>
next_st <= Init;
END CASE;
END PROCESS;
next_st_proc:
PROCESS (clk, reset)
BEGIN
IF reset = '1'
THEN present_st <= Init;
ELSIF (rising_edge(clk))
THEN present_st <= next_st;
END IF;
END PROCESS;
out_proc:
PROCESS (present_st)
BEGIN
CASE present_st IS
WHEN Init =>
output <= "000";
WHEN R =>
output <= "100";
WHEN RG =>
output <= "010";
WHEN G =>
output <= "001";
WHEN GR =>
output <= "010";
END CASE;
END PROCESS;
END rtl;
The resulting CA graph obtained during compilation in the Quartus II package is shown in Figure 5 (Tools - Netlist Viewers - State Machine Viewer menu).
Figure 5 - Digital machine with three processes. Compilation
result The result of the synthesis of the program shown in the listing above is shown in Fig. 6 (Tools menu - Netlist Viewers - Technology Map Viewer). To facilitate understanding in the figure, I / O elements are denoted as IO, triggers as FF, and logic elements as LE. As you can see as a result of the synthesis, we get a scheme of 5 triggers for storing the states of a digital machine (in the case of the One Hot coding method) and two logic elements for implementing a transition scheme and generating output signals.

Figure 6 - Digital machine with three processes. Technology map viewer
The description with the help of two processes (Fig. 6) assumes that the block of transition logic and the state register are combined into one process, in which, using the case operator, the future state of the digital automaton is selected. Since there is no need to separate the signals of the current and future states, these two signals are replaced by one, state , in which the state of the digital machine is stored.
The listing below shows an example of a CA description with asynchronous reset. As a result of compilation, the same result will be obtained as in the previous case - Fig. 7.

Figure 7 - Digital machine with two processes
Description of CA using two processes. Asynchronous reset
LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
ENTITY traffic IS
PORT(clk : IN std_logic;
cnt : IN std_logic;
reset : IN std_logic;
output : OUT std_logic_vector(2 downto 0)
);
END ENTITY;
ARCHITECTURE rtl OF traffic IS
TYPE state_type IS (Init, R, RG, G, GR);
SIGNAL state: state_type;
BEGIN
state_proc:
PROCESS (clk, reset)
BEGIN
IF reset = '1'
THEN state <= Init;
ELSIF (rising_edge(clk)) THEN
CASE state IS
WHEN Init =>
IF cnt = '1'
THEN state <= R;
ELSE
state <= Init;
END IF;
WHEN R =>
IF cnt = '1'
THEN state <= RG;
ELSE
state <= R;
END IF;
WHEN RG =>
IF cnt = '1'
THEN state <= G;
ELSE
state <= RG;
END IF;
WHEN G =>
IF cnt = '1'
THEN state <= GR;
ELSE
state <= G;
END IF;
WHEN GR =>
IF cnt = '1'
THEN state <= R;
ELSE
state <= GR;
END IF;
END CASE;
END IF;
END PROCESS;
out_proc:
PROCESS (state)
BEGIN
CASE state IS
WHEN Init =>
output <= "000";
WHEN R =>
output <= "100";
WHEN RG =>
output <= "010";
WHEN G =>
output <= "001";
WHEN GR =>
output <= "010";
END CASE;
END PROCESS;
END rtl;
A digital machine with synchronous reset described by two processes is shown below. The synthesis results from Technology Map Viewer are shown in Fig. 8, from which it can be seen that the size of the combination part of the automaton has increased significantly compared to an automaton with asynchronous reset.
Description of CA using two processes. Synchronous reset
LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
ENTITY traffic IS
PORT(clk : IN std_logic;
cnt : IN std_logic;
reset : IN std_logic;
output : OUT std_logic_vector(2 downto 0)
);
END ENTITY;
ARCHITECTURE rtl OF traffic IS
TYPE state_type IS (Init, R, RG, G, GR);
SIGNAL state: state_type;
BEGIN
state_proc:
PROCESS (clk)
BEGIN
IF (rising_edge(clk)) THEN
IF reset = '1'
THEN state <= Init;
ELSE
CASE state IS
WHEN Init =>
IF cnt = '1'
THEN state <= R;
ELSE
state <= Init;
END IF;
WHEN R =>
IF cnt = '1'
THEN state <= RG;
ELSE
state <= R;
END IF;
WHEN RG =>
IF cnt = '1'
THEN state <= G;
ELSE
state <= RG;
END IF;
WHEN G =>
IF cnt = '1'
THEN state <= GR;
ELSE
state <= G;
END IF;
WHEN GR =>
IF CNT = '1'
THEN state <= R;
ELSE
state <= GR;
END IF;
END CASE;
END IF;
END IF;
END PROCESS;
out_proc:
PROCESS (state)
BEGIN
CASE state is
WHEN Init =>
output <= "000";
WHEN R =>
output <= "100";
WHEN RG =>
output <= "010";
WHEN G =>
output <= "001";
WHEN GR =>
output <= "010";
END CASE;
END PROCESS;
END rtl;

Figure 8 - The result of the synthesis of a digital machine with synchronous reset
Description of a digital machine using one process assumes that all the logic is in one process. Some authors [5] believe that using a single process to describe a digital machine is simpler and more easily describe and debug a digital machine. This statement is true for small digital vending machines. As the number of states increases and one process is used, the readability of the code deteriorates. Because even the ancient Romans used the rule "Divide and conquer" when describing digital machines.
Another argument that is made in favor of using a single process when describing a digital automaton is that this option involves the use of synchronous output signals. This condition is not mandatory for all CAs and can be easily achieved, which was shown above when discussing the logic of the formation of output signals.
And yet, to complete the image, we give an example of a description of a digital machine with asynchronous reset using a single process.
Description of CA in one process
LIBRARY IEEE;
USE ieee.std_logic_1164.ALL;
ENTITY traffic IS
PORT(clk : IN std_logic;
cnt : IN std_logic;
reset : IN std_logic;
output : OUT std_logic_vector(2 downto 0)
);
END ENTITY;
ARCHITECTURE rtl OF traffic IS
TYPE state_type IS (Init, R, RG, G, GR);
SIGNAL state: state_type;
BEGIN
PROCESS (clk, reset)
BEGIN
IF reset = '1'
THEN state <= Init;
ELSIF (rising_edge(clk)) THEN
CASE state IS
WHEN Init =>
IF cnt = '1'
THEN state <= R;
ELSE
state <= Init;
END IF;
output <= "000";
WHEN R =>
IF cnt = '1'
THEN state <= RG;
ELSE
state <= R;
END IF;
output <= "100";
WHEN RG =>
IF cnt = '1'
THEN state <= G;
ELSE
state <= RG;
END IF;
output <= "010";
WHEN G =>
IF cnt = '1'
THEN state <= GR;
ELSE
state <= G;
END IF;
output <= "001";
WHEN GR =>
IF cnt = '1'
THEN state <= R;
ELSE
state <= GR;
END IF;
OUTPUT <= "010";
END CASE;
END IF;
END PROCESS;
END rtl;
The result of compiling the program is shown in the figure \ ref {FSM_1process_TMView}. Obviously, the result turned out to be the same as when describing using two processes with the only difference - triggers for the output register were added.

Figure 9 - Digital machine with one process
Let us summarize the small results of our research.
First and foremost. A digital machine exists! We saw him in picture 5.
Second. Descriptions using two and three processes give the same result, and the choice of description method depends on the preferences of the developer.
The third. You need to be very careful about the initial reset of the machine and the description of unused states.
Fourth. Description using one process leads to the emergence of registers for the output signals of the digital machine.
List of references.
1. Altera. Quartus II Handbook Version 10.0 Volume 1: Design and Synthesis Vol. 1, 2010 - 1820 p.
2. B. Cohen. VHDL Coding style and Methodologies. Kluwer Academic Publishers. 2002 - 454 p.
3. DL Perry. VHDL programming by example. New York: McGraw-Hill, 2002.- 476 p.
4. DJ Smith. HDL chip design: a practical guide for designing, synthesizing, and simulating ASICs and FPGAs using VHDL or Verilog. Madison, AL: Doone Publications, 1996 .-- 448 p.
5. A. Taylor. How to Implement State Machines in Your FPGA. Xcell 81 (4), p. 52-57.
6. Xilinx. VHDL Reference Guide. XST User Guide.
7. K. G. Samofalov. Applied Theory of Digital Automata. M.:, 1987.375 s.
PS The PDF version is here .
