3/14/15 9:26:53 Celebrating the “Pi Day” of the century, as well as a story about how to get your very personal piece of pi

Translation of Stephen Wolfram's post " Pi or Pie ?! Celebrating Pi Day of the Century (And How to Get Your Very Own Piece of Pi) "
I express my deep gratitude to those who helped me make this translation: Kurban Magomedov and Olga Lavrenyuk .

This Saturday will be the "Pi Day" of the century. Date 3/14/15 in the format month / day / year sets the first digits of the number π = 3.1415 ... And 9: 26: 53.589 ... in the morning will be "super moment of the day of Pi".


Thanks to Mathematica and Wolfram | Alpha , I’m sure that our company has given out π more times to the world than any other organization in history. Therefore, of course, we have to do a little special (SXSW event) for this special Pi Day.

Corporate confusion

One of my tasks as CEO is to come up with ideas and I spent decades building an organization that would bring them to life well. So, a few weeks ago I attended a meeting dedicated to upcoming corporate events and someone noticed that Pi Day (3/14) will be held during the large annual SXSW festival (South by Southwest) in Austin (Texas). I said (well, or at least I thought I said it), "We should have a big pi to celebrate Pi Day" <uses the untranslatable pun word pi - pie, which is important in the future> .

I did not think about this anymore, but after a couple of weeks we had another meeting about the current affairs of the company. One of the items on the agenda was just Pi Day. The person who leads our group, which is responsible for all kinds of events, started talking about the fact that it would be difficult to find a bakery in Austin that would make a fairly large pie. I exclaimed, “What are you talking about?” and then added, “You didn’t understand at all what I had in mind!”

I think that in our " English-speaking" world, the problem of <what is understood by> Pi is very common. Siri speech recognition system sends to the Wolfram | Alpha a lot of the "pie" of requests (pie) , which we have interpreted as the number Pi (pi) . There is also a single board computerRaspberry Pi preinstalled on Wolfram Language . It is even more confusing to my life that my personal file server was called “pi” for many years.

After this error pi (e), we continued the meeting and came up with many ideas on how to celebrate Pi Day. We have already rented a small venue on the territory of the SXSW festival and we wanted to make the most interesting “countdown to Pi Day” that is possible. We decided to make a large number of edible “pixel” cakes, which will be combined in the form of the Pi number into one big cake. Of course, there will also be a special Pi-selfie platform in the form of the Stonehenge-like Pi number, as well as a cake decorated with the Pi number in the form of Wolfie<Wolfram Language logo> for extra selfies. And of course we will do different things on the Raspberry Pi.

A piece of pi for each

I am sure that at the SXSW festival we all will get a lot of “pi-pleasure”. But we also want everyone in the world to take part in the celebration of Pi Day. We were tormented by the question “What could someone do with the number pi?”. In fact, in a sense, anyone can do anything with the Pi number. Say, in addition to the fact that the number Pi has infinitely many signs in its notation, their infinite sequence, in general, is completely random . So, for example, it will meet any predetermined sequence of numbers.

How about giving people a personal connection with this piece of math? The day of Pi occurs on the day that corresponds to the first digits of Pi. But any date is present somewhere in the record of the number Pi. So, we thought: “Why not give people the opportunity to find a place where their birthday appears on the number pi record (or any other date) and then create, say, personalized pi-shirts and pi-posters?”

In Wolfram Language, it’s very easy to find the position that your birthday takes in π. In general, any date in the format mm / dd / yy will be found among the first 10 million digits of the number Pi. On my desktop computer (Mac Pro), it took 6.28 seconds to calculate these 10 million digits of Pi number (2π ?!)

Below is the Wolfram Language code that allows you to get this result and present it as a string (discarding the integer and fractional parts, which is in second place in the resulting string):



Now it’s easy to find any “birthday-string”



So, for example, my birthday occurs for the first time in the record of the number π starting with the number 151 653.

How to visually display this? It depends on how “pi-lucky” you are. Say, for those born on 4/15/92, their birthday is already at position 3. People born on November 23, 1960 have a "birthday string" that starts only from 9 982 546 digits of Pi. In this case, in fact, most people have birthdays that are “quite far away” in the record of the number π (on average, these are positions of about 306,150).

Our main artist, who has been working with us for a very long time, had an idea to use a spiral that twists first inward and then outward, in order to display the beginning and end of such long sequences of numbers. And almost immediately he wrote the code that creates it (one of the most amazing things about Wolfram Language is that even people without a technical background can easily write their own code ...).



He then deployed his code on the Internet. Thanks to the Wolfram Programming Cloud , this was essentially done in just one line of code. Now, you can go to this MyPiDay.com site ...

... and get your own piece of pi!



Then you can share the image or order a T-shirt with it:

Pi science

Although we already talk a lot about the number Pi, I can not resist to talk a little about the number Pi from a scientific point of view. But, for starters, we answer the question: why is the number Pi so known? Yes, this is the ratio of the circumference to its diameter. And this in itself means that the number Pi occurs in billions of scientific formulas . But that's not all. (Say, for example, most people have never heard of an analogue of the number π for an ellipse - the so-called full elliptic integral of the second kind).

It is more interesting that the number π occurs in a significant number of mathematical constructions- including many such that seem to have nothing to do with circles. Such as, say, the sum of negative degrees or the limits of some sequences, or the likelihood that a randomly selected fraction will be irreducible.

If you just look at the sequence of digits of the number Pi 3.1415926 ...., then at first glance there is nothing special about it. But suppose we start to create formulas randomly and then we will perform traditional mathematical operations on them, such as, say, summing series, searching for integrals, limits, etc. We get a lot of answers like 0 or 1/2 or. But at the same time there will also be many cases when we cannot find the result in some closed form, but only numerically. But in cases where it can be obtained, my experience tells me that very often it will contain the number π.

Several other constants will also appear frequently, say - the number e (2.1718 ...) , the Euler-Mascheroni constant (0.5772 ...) or the Catalan constant (0.9159 ...) . But the number π appears clearly more often .

Perhaps mathematics could have another form. But, at least with the mathematics that we humans have created, the number π is a very common building brick, and it is natural that we gave it a name and that it became known so much that we set aside a separate day for celebrating this number.

What about the other constants? "Birthday strings" will, of course, occur in different positions of various constants. And, just as the Wolfram | Alpha service tries to find a closed form for a certain decimal fraction , you can also find the position of a certain sequence of digits inside other constants. So, for example, my birthday is at position 151 653 in number π, 241 683 in number e , 45 515 in , 40 979 in ζ (3) ... and 196 in1601th Fibonacci number .

Randomness in π

Let's say we plot a function that increases whenever the digit of π is greater than or equal to five and decreases otherwise:



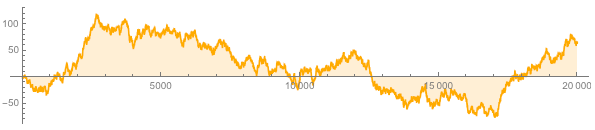
The graph looks like a random walk. At the same time, all statistical and cryptographic random tests that were performed on the digits of Pi (excluding tests that simply ask "are these digits from pi?") Confirm this assumption.

Why is this happening? There are simple procedures that generate Pi numbers. But it is striking that even though these procedures are simple, the result of their implementation is complex to such an extent that it seems completely random. In the past, there were no circumstances in which people would reason about such behavior. But it was precisely the study of such systems that I spent many years and wrote the book A New Kind of Science(A new kind of science). In a sense, the fact that anyone can find their birthday in the Pi number is directly related to concepts, such as, say, the Principle of Computational Equivalence , which I put forward in my book.

SETI and digits pi

Of course, just because we never saw any pattern in the numbers of Pi, this does not mean that such a pattern does not exist. In fact, it is still possible that if we did a sufficiently large search, we could find somewhere far in the numbers of Pi some kind of lurking, strange pattern.

What would that mean? There is a science fiction answer at the end of the book’s version of Contact" Карла Сагана. В книге, поиск внеземного разума заканчивается установлением контакта с межзвездной цивилизацией, которая создала удивительные артефакты — после этого объясняется, что самое важное, что было обнаружено, закодировано как раз в далеких цифрах числа Пи, в которых они нашли разумные послания, такие как, скажем, закодированное изображение окружности.

Вначале можно подумать, что поиск «разума» в цифрах числа Пи — абсурд. Ведь, в конце концов, существует вполне определенный простой алгоритм, который генерирует эти цифры. Но если мои подозрения на этот счет верны также, как и подозрения насчет всей нашей Вселенной, то на самом деле каждая деталь ее истории, в принципе, вычислима так же, как цифры числа Пи.

Now we know that in our Universe we ourselves act as an example of the mind. SETI (Search for Extraterrestrial Intelligence) is simply trying to find other examples. This task is well defined if we are looking for a "human type mind." But, in accordance with what my Principle of Computational Equivalence suggests , I think that in general it is practically impossible to make an exact distinction between what should be considered “reasonable” and what is considered “simply computable”.

If age-old mathematical suspicionsas to the fact that the digits of Pi are “normal”, then this will automatically mean that any sequence of digits will necessarily occur sooner or later among the digits of Pi, including all the works of Shakespeare, or any other legacy of any possible civilization. But can there be any other structure - perhaps even superimposing on normality - which, for example, can serve as evidence of the appearance of “reasonable” complexity?

Although it may be conceptually simple, it certainly seems a lot weirder to look for the possibility of a rational humanoid civilization in Pi numbers than in the physical Universe observed by SETI. But if we generalize what we consider reasonable, the situation becomes much less obvious.

Of course, if we observea complex signal from the pulsar magnetosphere, we say that it is “just physics”, and not the result of the evolution of “magnetohydrodynamic civilization”. Similarly, if we observe some complex structure in the numbers of Pi, we say that it is “just mathematics” and not the result of the life of some “number-theoretical civilization”.

We can move from a sequence of digits of the Pi to representations of any mathematical constant, which are easy to set using traditional mathematical operations. In some cases, there are certain patterns in such representations. But often everything again looks by chance. And the structure search project in such cases is generally similar to the SETI project in the physical Universe. (One of the differences, however, is that the number π, as an object for study, was chosen by us as a result of the structure of our physical Universe, our brain and our mathematical development. The Universe itself probably does not have the opportunity to make such a choice, which is given to us implicitly because we exist in it.)

I spent a lot of time searchingpatterns in the representation of numbers such as pi. I did not find anything significant. I think it is unnecessary to say that any patterns are generally easy to find. And there is a chance that it will take an effort as great as in the SETI project to detect them.

But now, let's celebrate the Pi Day of our century and enjoy things like searching for “birthday strings” in the pi number entry . Of course, someone, like me, can only hope that by the next Day of the Pi century , which will be held in 2115, we will succeed in the SETI or “SETI among numbers” project ...

Resources for learning Wolfram Language ( Mathematica) in Russian: habrahabr.ru/post/244451