Machine Learning - 2. Nonlinear Regression and Numerical Optimization
- Tutorial
A month has passed since the appearance of my first article on Habré and 20 days from the moment of the appearance of the second article about linear regression . Statistics on audience views and target actions are accumulated, and it was she who served as the starting point for this article. In it, we briefly consider an example of nonlinear regression (namely, exponential) and with its help we construct a conversion model by distinguishing two groups among users.
When it is known that a random variable y depends on something (for example, on time or on another random variable x) linearly, i.e. according to the law y (x) = Ax + b, then linear regression is applied (as in the previous articlewe built the dependence of the number of registrations on the number of views). For linear regression, the coefficients A and b are calculated using well-known formulas. In the case of a regression of another kind, for example, exponential, in order to determine unknown parameters, it is necessary to solve the corresponding optimization problem: namely, within the least squares (LSM) method, the problem of finding the minimum sum of squares (y (x i ) - y i ) 2 .
So, here is the data we will use as an example. Peaks in attendance (a number of Views, a red dotted line) occur at the time of publication of articles. The second row of data (Regs, with a factor of 100) shows the number of readers who performed a certain action after reading (registering and downloading Mathcad Express - with it, by the way, you can repeat all the calculations of this and previous articles). All pictures are screenshots of Mathcad Express, and you can take the file with calculations here .

With a green arrow on the graph, I designated a piece of data for which we will build a nonlinear regression. According to the model that we will take as a basis, after a short transition period after the publication of the publication, the number of views decreases with time approximately by an exponential law:
Views ≈ C 0 ∙ exp (C 1 ∙ t).
The justification of this model is postponed until one of future articles, when it comes to the Poisson random process.
It is clear that for analysis it is necessary to select the fragment that corresponds to the model (too close to the initial peak and without summing with the statistics of visits after the second article). It is this gap that is highlighted by a green arrow on the first chart, and on a larger scale it looks like this:

Exponential regression, I recall, will determine the graph of such an exponential function, which will be “on average” closest to the shown experimental points. In order to find the regression coefficients, it will be necessary to solve the optimization problem of finding the minimum of the objective function:
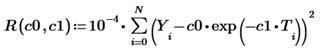
(T, Y) is an array of N experimental points, and we introduced the factor for convenience (it does not affect the position of the minimum). Further, of course, we could immediately write one or two lines of code with a built-in minimum search function to get the desired C0 and C1, however, we use the free Mathcad Express, where they are all turned off, so let's go a little more cumbersome (but easier to understand and visual) way.
First, let's see how the function R (c0, c1) behaves. To do this, we fix several values of c0 and construct for each of them a graph of the function of one variable R (c0, x).
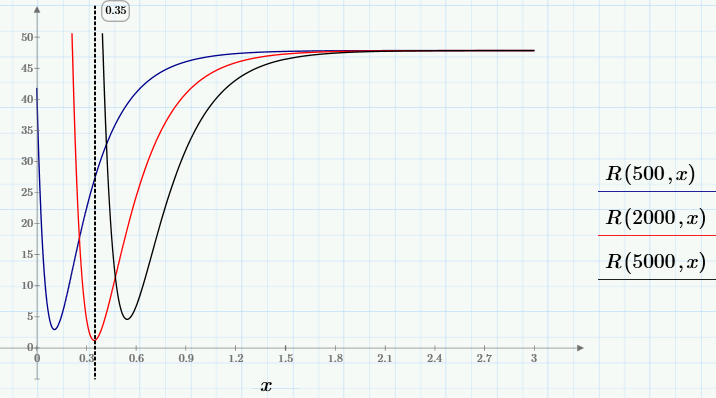
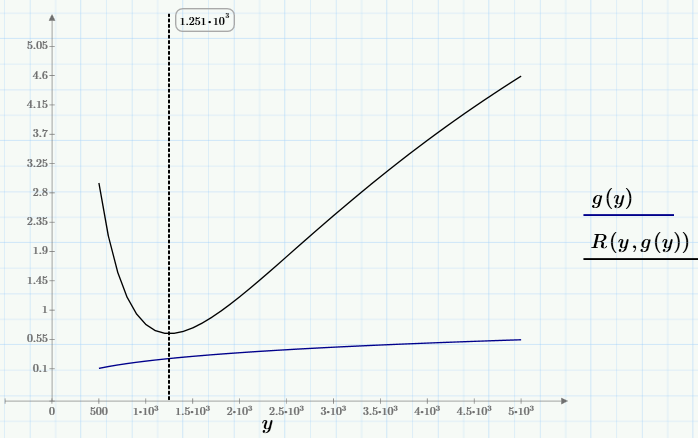
It can be seen that for selected c0 any of the graphs in the family has one minimum whose position x depends on c0, i.e. we can write x = g (c0). The deepest minimum, i.e., the minimum of R (c0, g (c0)) ~ min will be the desired global minimum. We need to find him to solve the problem. To find the global minimum, first (using the tools available in Mathcad Express) we define the user-defined function g (y), and then we find the minimum R (y, g (y)).
I will not dwell on the numerical algorithm for calculating the minimum (anyone interested, it is shown in the first line of the next screenshot). The solution of the problem (point, in the chosen notation c0 = y0 and c1 = x0), the value of the objective function at this point and the regression graph are shown below:
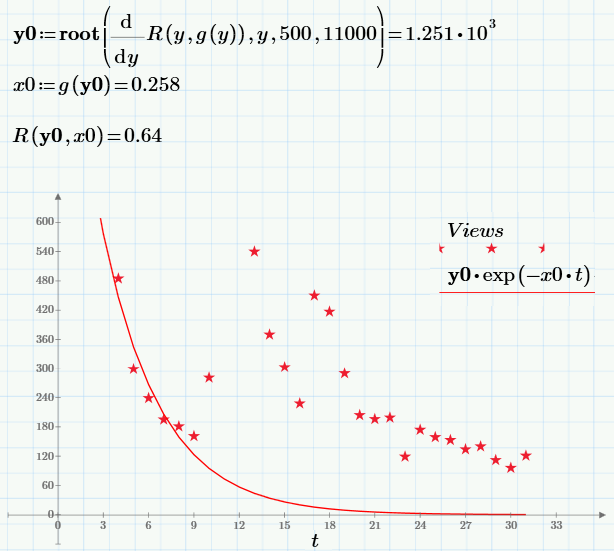
Can we get the result? Most likely not, since the constructed regression does not fit very well on the experimental points. The “tail” interferes, which differs greatly in regression (the exponent quickly drops to almost zero) and data (as you can see, even after a considerable time, the number of views is non-zero, but is about a hundred).
Therefore, to improve the result, let's improve the model. We assume that the model of the number of times an article is viewed is the sum of visits going through two channels:
This third parameter c2 can just be determined from the analysis of the “tail” of the data when there are practically no Poisson visitors, just as the average value of the views over the last 10 days of observation.
Finally, knowing c2, we can construct a refined regression of the form
Views ≈ c0 ∙ exp (c1 ∙ t) + c2,
repeating the algorithm described above completely:
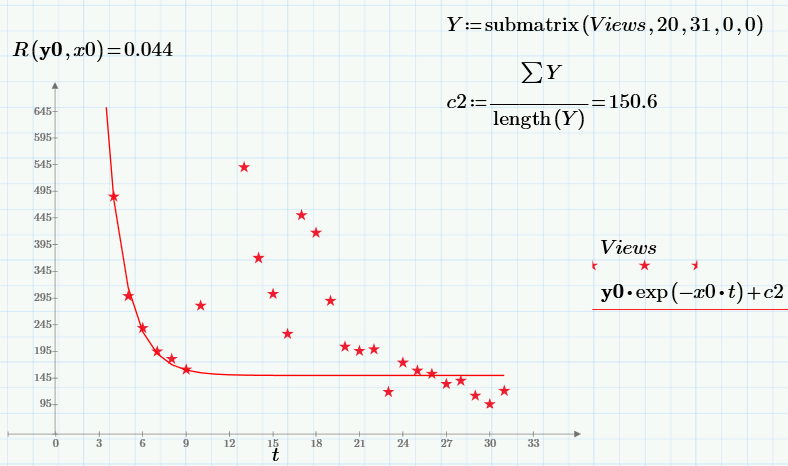
Note that the value of the objective function at a minimum (i.e., the sum of squared residuals) decreases compared with the case c2 = 0 more than an order of magnitude!
In conclusion, I will give the result of the built-in expfit function for finding exponential regression (available in the commercial version of Mathcad Prime). The result of the work is shown on the graph by a green dotted line, and our result (the same as on the previous graph) is shown by a red solid line.

All pictures are screenshots of Mathcad Express (the calculations themselves can be taken here, repeated, and if desired, changed and used for your needs). Do not forget to set c2 = 0 or c2 = 150 at the beginning of the calculations to select the first or second model, respectively.
When it is known that a random variable y depends on something (for example, on time or on another random variable x) linearly, i.e. according to the law y (x) = Ax + b, then linear regression is applied (as in the previous articlewe built the dependence of the number of registrations on the number of views). For linear regression, the coefficients A and b are calculated using well-known formulas. In the case of a regression of another kind, for example, exponential, in order to determine unknown parameters, it is necessary to solve the corresponding optimization problem: namely, within the least squares (LSM) method, the problem of finding the minimum sum of squares (y (x i ) - y i ) 2 .
So, here is the data we will use as an example. Peaks in attendance (a number of Views, a red dotted line) occur at the time of publication of articles. The second row of data (Regs, with a factor of 100) shows the number of readers who performed a certain action after reading (registering and downloading Mathcad Express - with it, by the way, you can repeat all the calculations of this and previous articles). All pictures are screenshots of Mathcad Express, and you can take the file with calculations here .

With a green arrow on the graph, I designated a piece of data for which we will build a nonlinear regression. According to the model that we will take as a basis, after a short transition period after the publication of the publication, the number of views decreases with time approximately by an exponential law:
Views ≈ C 0 ∙ exp (C 1 ∙ t).
The justification of this model is postponed until one of future articles, when it comes to the Poisson random process.
It is clear that for analysis it is necessary to select the fragment that corresponds to the model (too close to the initial peak and without summing with the statistics of visits after the second article). It is this gap that is highlighted by a green arrow on the first chart, and on a larger scale it looks like this:

Exponential regression, I recall, will determine the graph of such an exponential function, which will be “on average” closest to the shown experimental points. In order to find the regression coefficients, it will be necessary to solve the optimization problem of finding the minimum of the objective function:
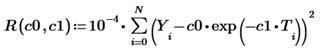
(T, Y) is an array of N experimental points, and we introduced the factor for convenience (it does not affect the position of the minimum). Further, of course, we could immediately write one or two lines of code with a built-in minimum search function to get the desired C0 and C1, however, we use the free Mathcad Express, where they are all turned off, so let's go a little more cumbersome (but easier to understand and visual) way.
First, let's see how the function R (c0, c1) behaves. To do this, we fix several values of c0 and construct for each of them a graph of the function of one variable R (c0, x).

It can be seen that for selected c0 any of the graphs in the family has one minimum whose position x depends on c0, i.e. we can write x = g (c0). The deepest minimum, i.e., the minimum of R (c0, g (c0)) ~ min will be the desired global minimum. We need to find him to solve the problem. To find the global minimum, first (using the tools available in Mathcad Express) we define the user-defined function g (y), and then we find the minimum R (y, g (y)).

I will not dwell on the numerical algorithm for calculating the minimum (anyone interested, it is shown in the first line of the next screenshot). The solution of the problem (point, in the chosen notation c0 = y0 and c1 = x0), the value of the objective function at this point and the regression graph are shown below:

Can we get the result? Most likely not, since the constructed regression does not fit very well on the experimental points. The “tail” interferes, which differs greatly in regression (the exponent quickly drops to almost zero) and data (as you can see, even after a considerable time, the number of views is non-zero, but is about a hundred).
Therefore, to improve the result, let's improve the model. We assume that the model of the number of times an article is viewed is the sum of visits going through two channels:
- channel with Poisson statistics Views ≈ с0 ∙ exp (с1 ∙ t);
- a channel with an approximately constant number of views (let's call it parameter c2).
This third parameter c2 can just be determined from the analysis of the “tail” of the data when there are practically no Poisson visitors, just as the average value of the views over the last 10 days of observation.
Finally, knowing c2, we can construct a refined regression of the form
Views ≈ c0 ∙ exp (c1 ∙ t) + c2,
repeating the algorithm described above completely:

Note that the value of the objective function at a minimum (i.e., the sum of squared residuals) decreases compared with the case c2 = 0 more than an order of magnitude!
In conclusion, I will give the result of the built-in expfit function for finding exponential regression (available in the commercial version of Mathcad Prime). The result of the work is shown on the graph by a green dotted line, and our result (the same as on the previous graph) is shown by a red solid line.

All pictures are screenshots of Mathcad Express (the calculations themselves can be taken here, repeated, and if desired, changed and used for your needs). Do not forget to set c2 = 0 or c2 = 150 at the beginning of the calculations to select the first or second model, respectively.
