Applied optimization practice and a bit of history
“A thousand dollars for one hit with a sledgehammer ?!” Cried out a surprised, but happy (and saved by solving the problem) steam engine engineer. “No, a strike costs $ 1, the rest is for knowing where, when and how to hit hard,” answered the old master.
Type of epigraph
In patenting, there is such a category of inventions when it is patented not what a person / team invented (it has been known for a long time, for example, glue), and not a new way to achieve an urgent goal (for example, sealing a wound from infection). And patented, for example, is the use of a well-known substance in a completely new (for a given substance), but also well-known and long known for achieving the goal application. “And let's try to seal the wound with BF-6 glue? ABOUT! And it turns out that it has bactericidal properties ... and the wound underneath breathes ... and heals faster! Stake and apply! ”
In applied mathematics, there are tools whose competent use allows you to solve a very wide range of various problems. I want to tell you about this. Maybe someone will run into the search for their non-trivial application of successfully mastered algorithms or techniques / programs. There will be few references to rigorous mathematical tools or relationships, a more qualitative analysis of the advantages and applications of the numerical method (s), which has played a large role in my life and become the basis for solving important professional problems.
Quite a long time ago (when defending a dissertation and working at a military-space enterprise, Krasnodar), a toolkit was developed for solving optimization problems - searching for a local extremum of a multi-parameter function on a certain set of restrictions for its parameters. Such methods are widely known, for example, almost everyone is familiar with the steepest descent method ( Gradient Descent ).
The software package (first Fortran, then Pascal / Modula 2, now the algorithm rested in a well-inherited, convenient and universal VBA / Excel) implemented several different well-known methods for finding extremums that successfully complemented each other on a very wide class of problems. They were easily interchangeable and installed on the stack (the next one started from the optimum found by the previous one, with a wide coverage of the possible initial values of the parameters), they quickly found a minimum and “squeezed” the objective function with a good guarantee of the globality of the found extremum.
For example, using this set of programs, a model of an autonomous system was built, consisting of solar panels, batteries (then only long-lasting nickel-hydrogen appeared), payload and control system (battery orientation and energy conversion for load). All this was driven in a given period of time under the influence of external weather conditions in a given area. For this, a weather model was also created (bymyself, 7 years after Bradley Efron, rediscovered ) using the " statistical bootstrap method". At the same time, as the initial" brick "for the model of the solar battery (and battery of batteries), models of real parameters of silicon wafers (batteries) were used, from which the batteries were assembled taking into account their statistical dispersion during production and assembly scheme. The model of the autonomous system allowed to evaluate the size and configuration of the solar and battery, sufficient to solve the tasks in the given conditions for the functioning of the system (here I directly physically recognized / remembered the cloth speech of Colonel the First department).
Measurements of silicon wafers of solar cells at the output of the process and identification of the parameters of the model of a single element by the optimization method made it possible to create an array of element parameters that describes the statistical parameters of the current process for the production of solar cells.
The mathematical model of the current-voltage characteristics (CVC) of the solar cell is well known, there are few parameters there. To select the parameters of the CVC model of a solar cell with a minimum standard deviation is the classic task of finding the minimum of the objective function (the total square of the deviations on the CVC).
The parameters of the finished solar battery obtained by the Monte Carlo method reflected the possible stochastic spread of its parameters for a given structure of the connection of elements. The construction of a battery model assembled from solar cell models made it possible, in particular, to solve the problems of estimating battery power losses due to damage (the war in Afghanistan was in full swing, and meteorites were flying in space) and losses due to partial shading (snow, foliage ), which led to the occurrence of dangerous breakdown voltages and the need to correctly place shunt diodes to reduce average power losses. All these were already stochastic tasks, i.e. requiring a huge amount of computation with different scatter of the initial parameters of the "bricks", battery connection schemes and influencing factors. It was unprofitable to “dance” from the primary identified model of the solar cell in such calculations, therefore, a chain of models was built: the primary silicon wafer, the entire battery (from if the structural diagram analysis was required), and the battery itself were assembled. The parameters of these models were identified using optimization methods, and the array of elements of the battery structure for its calculation was generated by the Monte Carlo method taking into account stochastic variations (array of parameters + statistical bootstrap).
The tasks being solved became more complicated. In the beginning there was an idea to make the most “computationally-intensive” parts of optimization methods in assembler, but as productivity grows, first a SM-computer (tasks were considered overnight) and then a PC (now the most complex tasks require an hour or two), the need to optimize the program optimization (a masterpiece of tautology) has disappeared. In addition, in most cases, the objective functions themselves are “computationally-intensive”.
Here it is necessary to return to the partially affected universality of optimization methods and relate them to other methods of numerical analysis. The main applications of the developed tools:
- identification of the parameters of the theoretical model according to the initial (experimental or calculated) data;
- data approximation, this is the same identification not only of the model, but of the parameters of a suitable (generally abstract) formula, for the purpose of smoothing / approximation, interpolation and extrapolation;
- numerical solution of systems of arbitrary (!) Equations.
It seems to be a little, but this class of problems “covers” a wide range of real applied problems of mathematics in industry, science, an example with an autonomous system model is evidence of this.
The arsenal of classical methods of numerical analysis has effective direct methods / approaches for solving some standard problems (for example, systems of equations with polynomials of low degrees), special program libraries have been developed for them. However, when the number of parameters / unknowns exceeds 4-5 (and the computational costs dramatically increase), and / or when the form of the equations is far from classical (not polynomials, etc.), and in life, as a rule, everything is more complicated (initial data noisy with errors and measurement errors), ready-made library programs are ineffective.
I will give in more detail one more example from the relatively recent application of the developed tools for solving optimization problems from life.
For a dissertation on experimental (field) data, the identification of a theoretical model was required, which was supposed to describe these data and made it possible to give real recommendations on improving the efficiency of an adjacent technological process. Every percentage of the improvement in the process justified the repeated trip to the field trials (and nearby beaches) by the first class through half the world and the acquisition of a chic Lexus jeep only for driving through the fields (and even with a nice long-legged blonde who knows how to cook borsch :) The problem was that there were several such models, the identification and quality of reproducing the experimental data could choose the applicability of one of them, and the parameters in these models were from 6 to 9, and the potentially most useful model according to the law of the sandwich was the most complex.
The following are the initial experimental data (X, Y, Z), 19 measurements:
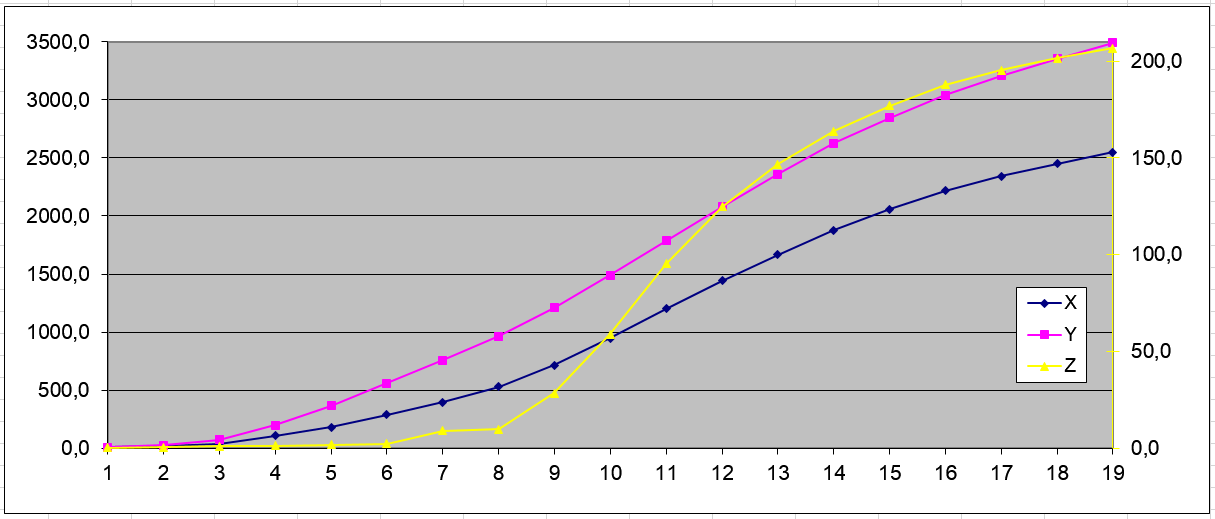
And an example of approximating a curve (U3 - experiment, U3R - calculation by model) when identifying the most complex nine-parameter model (a1 ... a9 - model parameters):

The formula of this model:
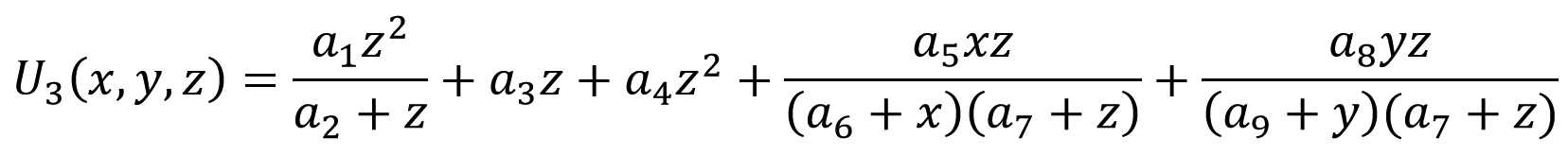
If you have a need for such work, I could do the calculations based on the data provided and send the results by e-mail to evaluate the advantages of the developed mat. apparatus.
This is a popular range of tasks in science, in production, in the preparation of dissertations, serious diplomas, data processing, model building. Moreover, any fraud is excluded, because according to the results provided, everyone can evaluate the calculation accuracy achieved in reality.
Describe your problems in data processing - and I will find how to get a solution, the program should work!
He is interested in receiving a side view of what is described, possibly, in new areas of application. I would be grateful for useful comments and cooperation.
Type of epigraph
In patenting, there is such a category of inventions when it is patented not what a person / team invented (it has been known for a long time, for example, glue), and not a new way to achieve an urgent goal (for example, sealing a wound from infection). And patented, for example, is the use of a well-known substance in a completely new (for a given substance), but also well-known and long known for achieving the goal application. “And let's try to seal the wound with BF-6 glue? ABOUT! And it turns out that it has bactericidal properties ... and the wound underneath breathes ... and heals faster! Stake and apply! ”
In applied mathematics, there are tools whose competent use allows you to solve a very wide range of various problems. I want to tell you about this. Maybe someone will run into the search for their non-trivial application of successfully mastered algorithms or techniques / programs. There will be few references to rigorous mathematical tools or relationships, a more qualitative analysis of the advantages and applications of the numerical method (s), which has played a large role in my life and become the basis for solving important professional problems.
Quite a long time ago (when defending a dissertation and working at a military-space enterprise, Krasnodar), a toolkit was developed for solving optimization problems - searching for a local extremum of a multi-parameter function on a certain set of restrictions for its parameters. Such methods are widely known, for example, almost everyone is familiar with the steepest descent method ( Gradient Descent ).
The software package (first Fortran, then Pascal / Modula 2, now the algorithm rested in a well-inherited, convenient and universal VBA / Excel) implemented several different well-known methods for finding extremums that successfully complemented each other on a very wide class of problems. They were easily interchangeable and installed on the stack (the next one started from the optimum found by the previous one, with a wide coverage of the possible initial values of the parameters), they quickly found a minimum and “squeezed” the objective function with a good guarantee of the globality of the found extremum.
For example, using this set of programs, a model of an autonomous system was built, consisting of solar panels, batteries (then only long-lasting nickel-hydrogen appeared), payload and control system (battery orientation and energy conversion for load). All this was driven in a given period of time under the influence of external weather conditions in a given area. For this, a weather model was also created (by
Measurements of silicon wafers of solar cells at the output of the process and identification of the parameters of the model of a single element by the optimization method made it possible to create an array of element parameters that describes the statistical parameters of the current process for the production of solar cells.
The mathematical model of the current-voltage characteristics (CVC) of the solar cell is well known, there are few parameters there. To select the parameters of the CVC model of a solar cell with a minimum standard deviation is the classic task of finding the minimum of the objective function (the total square of the deviations on the CVC).
The parameters of the finished solar battery obtained by the Monte Carlo method reflected the possible stochastic spread of its parameters for a given structure of the connection of elements. The construction of a battery model assembled from solar cell models made it possible, in particular, to solve the problems of estimating battery power losses due to damage (the war in Afghanistan was in full swing, and meteorites were flying in space) and losses due to partial shading (snow, foliage ), which led to the occurrence of dangerous breakdown voltages and the need to correctly place shunt diodes to reduce average power losses. All these were already stochastic tasks, i.e. requiring a huge amount of computation with different scatter of the initial parameters of the "bricks", battery connection schemes and influencing factors. It was unprofitable to “dance” from the primary identified model of the solar cell in such calculations, therefore, a chain of models was built: the primary silicon wafer, the entire battery (from if the structural diagram analysis was required), and the battery itself were assembled. The parameters of these models were identified using optimization methods, and the array of elements of the battery structure for its calculation was generated by the Monte Carlo method taking into account stochastic variations (array of parameters + statistical bootstrap).
The tasks being solved became more complicated. In the beginning there was an idea to make the most “computationally-intensive” parts of optimization methods in assembler, but as productivity grows, first a SM-computer (tasks were considered overnight) and then a PC (now the most complex tasks require an hour or two), the need to optimize the program optimization (a masterpiece of tautology) has disappeared. In addition, in most cases, the objective functions themselves are “computationally-intensive”.
Here it is necessary to return to the partially affected universality of optimization methods and relate them to other methods of numerical analysis. The main applications of the developed tools:
- identification of the parameters of the theoretical model according to the initial (experimental or calculated) data;
- data approximation, this is the same identification not only of the model, but of the parameters of a suitable (generally abstract) formula, for the purpose of smoothing / approximation, interpolation and extrapolation;
- numerical solution of systems of arbitrary (!) Equations.
It seems to be a little, but this class of problems “covers” a wide range of real applied problems of mathematics in industry, science, an example with an autonomous system model is evidence of this.
The arsenal of classical methods of numerical analysis has effective direct methods / approaches for solving some standard problems (for example, systems of equations with polynomials of low degrees), special program libraries have been developed for them. However, when the number of parameters / unknowns exceeds 4-5 (and the computational costs dramatically increase), and / or when the form of the equations is far from classical (not polynomials, etc.), and in life, as a rule, everything is more complicated (initial data noisy with errors and measurement errors), ready-made library programs are ineffective.
I will give in more detail one more example from the relatively recent application of the developed tools for solving optimization problems from life.
For a dissertation on experimental (field) data, the identification of a theoretical model was required, which was supposed to describe these data and made it possible to give real recommendations on improving the efficiency of an adjacent technological process. Every percentage of the improvement in the process justified the repeated trip to the field trials (and nearby beaches) by the first class through half the world and the acquisition of a chic Lexus jeep only for driving through the fields (and even with a nice long-legged blonde who knows how to cook borsch :) The problem was that there were several such models, the identification and quality of reproducing the experimental data could choose the applicability of one of them, and the parameters in these models were from 6 to 9, and the potentially most useful model according to the law of the sandwich was the most complex.
The following are the initial experimental data (X, Y, Z), 19 measurements:

And an example of approximating a curve (U3 - experiment, U3R - calculation by model) when identifying the most complex nine-parameter model (a1 ... a9 - model parameters):

The formula of this model:
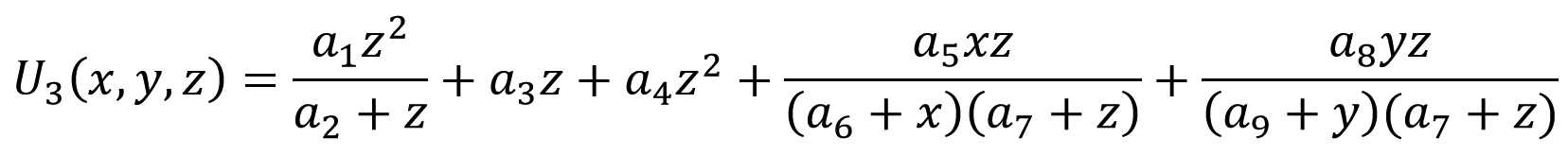
If you have a need for such work, I could do the calculations based on the data provided and send the results by e-mail to evaluate the advantages of the developed mat. apparatus.
This is a popular range of tasks in science, in production, in the preparation of dissertations, serious diplomas, data processing, model building. Moreover, any fraud is excluded, because according to the results provided, everyone can evaluate the calculation accuracy achieved in reality.
Describe your problems in data processing - and I will find how to get a solution, the program should work!
He is interested in receiving a side view of what is described, possibly, in new areas of application. I would be grateful for useful comments and cooperation.
