Search for similar documents with MinHash + LHS
In this post, I’ll talk about how to find similar documents using MinHash + Locality Sensitive Hashing. The Wikipedia description of LHS and Minhash abounds with an appalling amount of formulas. In fact, everything is quite simple.
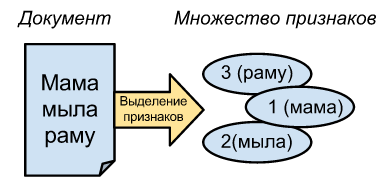
By a document in this article I mean plain text, but in the general case it can be any array of bytes. The thing is that to compare any document using MinHash, you must first convert it to many elements.
For texts, converting to multiple word IDs is a good idea. Say, “mom washed the frame” -> [1, 2, 3], and “mom washed” -> [1, 2].
The similarity of these sets is 2/3, where 2 is the number of similar elements, and 3 is the total number of different words.
You can also break these texts into N-grams, for example, “mom washed the frame” is divided into trigrams “mom, ama, ma_, a_m, ...”, which will give a similarity of 7/12.
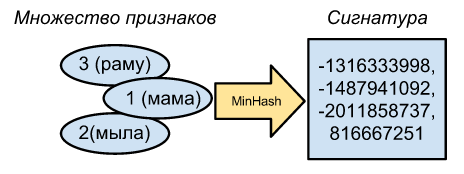
Captain evidence tells us that MinHash is the minimum hash of all the hashes of our set. Say, if we have a simple random hash function f (v) = v, then our sets of word IDs [1, 2, 3] and [1, 2] are transformed into a set of hashes [ 1078 , 2573, 7113] and [ 1078 , 2573 ], and for each set the minhash is 1078 . It seems easy.
The likelihood that the minimum hashes for the two sets coincide is exactly equal to the similarity of the two sets. I do not want to prove it, because I'm allergic to formulas, but this is very important.
Okay, having one minhash, we won’t do much, but it’s already clear that the same sets will give the same minhash, and for completely different sets and an ideal hash function it is guaranteed to be different.
To consolidate the result, we can take many different hash functions and find a minhash for each of them. Quite simply, you can get a lot of different hash functions by generating a lot of random, but different numbers, and put our first hash function on these numbers. Let's say we generate completely random numbers 700 and 7000, which will give us two additional hash functions. Then the minheshes for [1, 2, 3] will be (1078, 2573, 7113) -> 1078 , (1674, 2225, 6517) -> 1674 , (8046, 4437, 145) -> 145 , and for [1, 2 ] minheshes, its signature will be (1078, 2573) -> 1078 , (1674, 2225) -> 1674 , (8046, 4437) -> 4437. As you can see, the first two pairs of minhashes coincide, from which it is very roughly possible to assume that the similarity of the original sets is 2/3. It is clear that the more hash functions, the more accurately you can determine the similarity of the original sets.
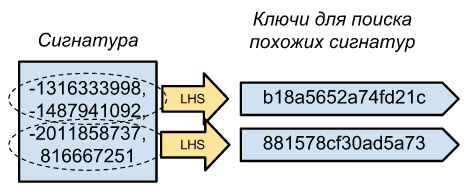
We can now determine how similar documents are using only their signatures (N minhash values), but what needs to be written in the key-value repository to be able to select from all more or less similar documents? If we use whole signatures as keys, then we will make a selection only from almost identical documents, because the probability that N minhesheh matches is equal to s ^ N where s is the identity of the documents.
The solution is simple - let's say our signatures consist of 100 numbers, we can divide it into several parts (say, 10 parts of 10 numbers), after which we make all these parts the keys of an entire signature.
That's all, now to determine that we already have a similar document in the database. It is necessary to obtain its signature of 100 minheshes, split into ten keys and for all the full signatures corresponding to them, calculate its similarity (the number of matching minheshes).
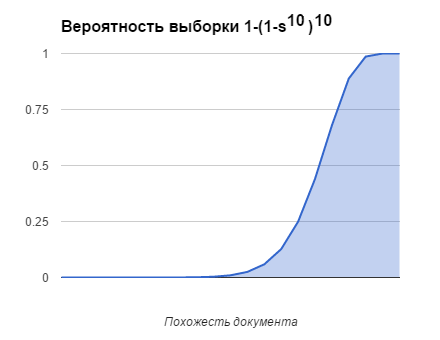
For ten keys with ten elements in each, the probability of selecting a document, depending on the similarity of the document, will be this:
1. Highlighting signs

By a document in this article I mean plain text, but in the general case it can be any array of bytes. The thing is that to compare any document using MinHash, you must first convert it to many elements.
For texts, converting to multiple word IDs is a good idea. Say, “mom washed the frame” -> [1, 2, 3], and “mom washed” -> [1, 2].
The similarity of these sets is 2/3, where 2 is the number of similar elements, and 3 is the total number of different words.
You can also break these texts into N-grams, for example, “mom washed the frame” is divided into trigrams “mom, ama, ma_, a_m, ...”, which will give a similarity of 7/12.
2. Creating a signature with MinHash

Captain evidence tells us that MinHash is the minimum hash of all the hashes of our set. Say, if we have a simple random hash function f (v) = v, then our sets of word IDs [1, 2, 3] and [1, 2] are transformed into a set of hashes [ 1078 , 2573, 7113] and [ 1078 , 2573 ], and for each set the minhash is 1078 . It seems easy.
The likelihood that the minimum hashes for the two sets coincide is exactly equal to the similarity of the two sets. I do not want to prove it, because I'm allergic to formulas, but this is very important.
Okay, having one minhash, we won’t do much, but it’s already clear that the same sets will give the same minhash, and for completely different sets and an ideal hash function it is guaranteed to be different.
To consolidate the result, we can take many different hash functions and find a minhash for each of them. Quite simply, you can get a lot of different hash functions by generating a lot of random, but different numbers, and put our first hash function on these numbers. Let's say we generate completely random numbers 700 and 7000, which will give us two additional hash functions. Then the minheshes for [1, 2, 3] will be (1078, 2573, 7113) -> 1078 , (1674, 2225, 6517) -> 1674 , (8046, 4437, 145) -> 145 , and for [1, 2 ] minheshes, its signature will be (1078, 2573) -> 1078 , (1674, 2225) -> 1674 , (8046, 4437) -> 4437. As you can see, the first two pairs of minhashes coincide, from which it is very roughly possible to assume that the similarity of the original sets is 2/3. It is clear that the more hash functions, the more accurately you can determine the similarity of the original sets.
3. Key Creation with Locality Sensitive Hashing

We can now determine how similar documents are using only their signatures (N minhash values), but what needs to be written in the key-value repository to be able to select from all more or less similar documents? If we use whole signatures as keys, then we will make a selection only from almost identical documents, because the probability that N minhesheh matches is equal to s ^ N where s is the identity of the documents.
The solution is simple - let's say our signatures consist of 100 numbers, we can divide it into several parts (say, 10 parts of 10 numbers), after which we make all these parts the keys of an entire signature.
That's all, now to determine that we already have a similar document in the database. It is necessary to obtain its signature of 100 minheshes, split into ten keys and for all the full signatures corresponding to them, calculate its similarity (the number of matching minheshes).
For ten keys with ten elements in each, the probability of selecting a document, depending on the similarity of the document, will be this:

