Lock-free data structures. Concurrent map: warm up
I was honored to be invited to speak at the first C ++ 2015 Russia conference on February 27-28. I was so arrogant that I asked for 2 hours to speak instead of the one that was supposed to be and stated the topic that interests me the most - competitive associative containers. These are hash set / map and trees. The organizer sermp went forward, for which many thanks to him.
How to prepare for such a challenging
Of course, you need to write down your thoughts, looking at the slides. And if something is written, then it would not be bad to publish. And if you publish, then on the hub
So, in the wake of C ++ 2015 Russia! The author’s presentation, I hope, without the author’s tongue-tied tongue, without notes and with deviations on the topic, written before the event, in several parts.
As a C ++ programmer, most of all from the standard library of containers I had to use not queues / stacks / decks / lists, but associative containers - hash set / map, they are also std :: unordered_set / map, and trees, that is, std :: set / map. As we know, the C ++ 11 standard guarantees us thread-safe operation with such containers, but very weak - only read-only, any change - only under external lock! In practice, such a guarantee is almost nothing, because if I have a read-only map, I will most likely make a sorted array and look for it using binary search - experience shows that it’s faster and the memory is used carefully and the processor cache nicely.
Is it possible to implement a concurrent map container without the need for external synchronization? Let's study this question.
To warm up, let's look at the internal structure of the hash map.
Hash table
The internal structure of the simplest hash map with a list of collisions is extremely primitive: there is an array
T[N], each element of which is a list. The entry to the table (index) is the hash value of the key. All keys with the same hash (modulo N) fall into the same list, called the collision list. 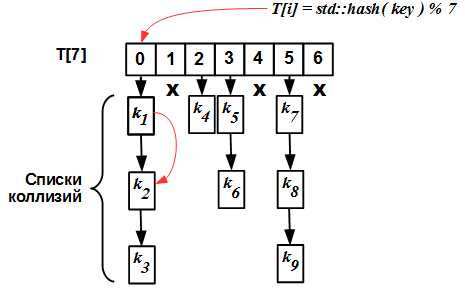
In general, the most important thing here is hidden inside the hash function. A hash map will work well if and only if the correct hash function has been selected for many keys. "Correct" - this means, first of all, "well-scattering" keys in the table cells. But from the point of view of increasing the level of competition, it does not matter to us how the hash function is arranged inside, so we won’t talk about it anymore.
Looking at the picture, you can immediately guess how to make a regular hash map competitive: instead of blocking access to the entire hash map, you can block it at the level of each table cell
T[N]. Thus, work with each specific list of collisions T[i]will be serialized, but work with different lists T[i]and T[j]( i != j) can be done in parallel. This technique is described in M. Herlihy and Nir Shavit's “The Art of Multiprocessor Programming” and is called striping.Claim publishers
Why has this work not yet been translated with us, although in the original it has already stood two editions ?! This fundamental work from very famous authors in the world is an analogue of Knut’s monumental monograph, but for parallel algorithms, an invaluable guide for students and anyone who wants to understand “how it works,” a launching pad for growing domestic personnel.
No, we will publish the waste paper “C ++ in 35 minutes for dummies”! Dummies don't need C ++ !!! And without such books we will only have teapots. This disclaimer does not concern readers of a habr.
No, we will publish the waste paper “C ++ in 35 minutes for dummies”! Dummies don't need C ++ !!! And without such books we will only have teapots. This disclaimer does not concern readers of a habr.
Striped map
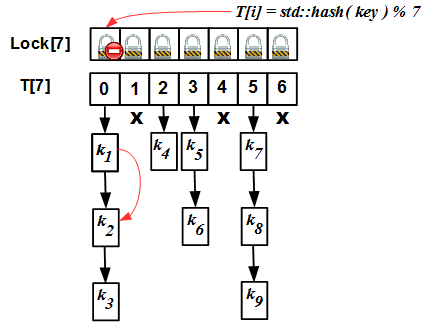
So, in the striping technique, we have two arrays - an array of locks
Lock[N]and a hash table itself T[N]. Initially, the size of these two arrays is the same (this is an important requirement, we will see why later). The internal algorithm of operation is simple: for any operation (insert / erase / find), we calculate the hash value of the ikey modulo N, block the mutex Lock[i]and go to perform the operation in the list T[i]. But there is one “but”: the hash table needs to be expanded from time to time. The criterion for the need for expansion is the so-called load factor: the ratio of the number of elements in the hash map to sizeNhash tables. If we do not expand the table, our collision lists will become very large, and all the benefits of the hash map will turn into a pumpkin: instead of evaluating O (1) for the complexity of the operation, we will get O (S / N), where S is the number of elements in the table, that for S >> N and constant N it is equivalent to O (S), that is, the complexity of a linear search! This is unacceptable. To combat this phenomenon, rehashing is required: increase N if the load factor exceeds a certain threshold value, and rebuild the hash table under new hash values std::hash(key) % N'. The rehashing algorithm for striped map is as follows:
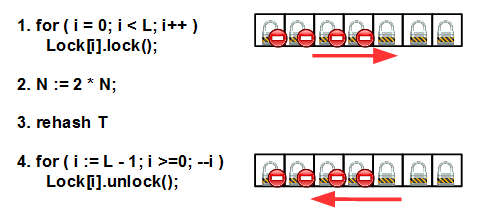
First, we block all mutexes from left to right; then increment N by an integertimes (an integer is important, see below), rebuild the hash table and, finally, unlock all the mutexes in the reverse order - from right to left. Do not forget that the main reason for deadlock is the non-observance of the lock / unlock order of several mutexes.
Locking all mutexes here is important so that no one bothers us doing rehashing. Rehashing is a rather difficult operation and redistributes the keys in the cells of the new table
T[N']. Note that we talked about increasing the size of the hash table above, but didn’t say anything about increasing the size of the lock array
Lock[N], it’s no accident: the fact is that the size of the lock array does not change . 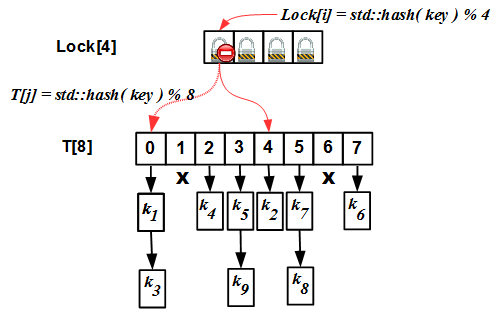
If the array sizes
Lockand Tdifferent, then , in principle,possible that different mutex Lock[i], and Lock[j]corresponds to the same cell T[k]that breaks down all our slender algorithm. For this to be unacceptable, it is required:- Initially, the sizes of arrays
Lockand are theTsame and equalN - When rehashing, the new size of the
N'array isTcalculated asN' = k * N, wherekis a natural number (usually 2).
Under these conditions, we always have the size of the array a
Tmultiple of the size of the array Lock(which does not change); based on the properties of arithmetic modulo, it is easy to prove that in this case the same cell T[k]cannot correspond to different mutexes Lock[i]and Lock[j].Refinable hash map
The authors of “The Art of Multiprocessor Programming” go further, solving the rehashing problem for the array
Lock, that is, proposing an algorithm that allows increasing the size Lock[]along with increasing the hash table. They call this algorithm the refinable hash map. Interested in sending to the original.The striping algorithm easily extends to other data structures, such as trees:

The idea is very simple: each element of the
Lock[L]mutex array protects its tree. The input to Lock[L]is the hash value of the key (modulo L). Lock[i]By blocking , we gain access to the corresponding tree, in which we perform the required action.libcds
The libcds library has implementations of striped and refinable hash set / map, as well as adapters for all associative containers from STL and boost, including intrusive ones.
The striping technique is not bad, but it has a significant flaw in terms of the series of articles on lock-free data structures - it is blockable. Is it possible to come up with a lock-free algorithm for hash map? ..
Lock-free ordered list
Let's take another look at the hash map internal structure:

For now, let's leave rehashing questions out of the way, we will assume that we know a priori the number of elements in the hash table and have a good hash function for our set of keys. Then to build a lock-free hash map we need a little - a lock-free list of collisions. A list of collisions is nothing more than an ordered (by key), simply connected list. We will try to build it, after T. Harris and M. Michael .
A search on a lock-free list is pretty trivial: a linear walk through the list, starting from its head. Given that we use atomic operations and one of the safe deletion schemes (Hazard Pointer, user-space RCUor similar), the search algorithm is not much different from ordinary search in an ordered list (in fact, if you look at the code, it is strong, but this is a lock-free fee).
Inserting a new element does not present any problems either:
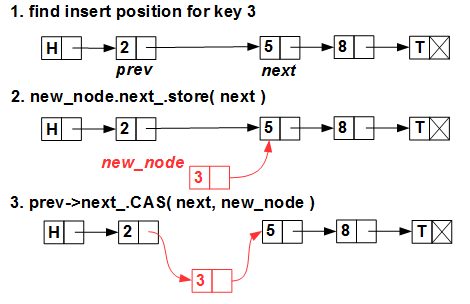
We look for the insertion position (remember that the list is ordered), create a new element and insert it with a single CAS primitive (compare-and-swap, which is the same
std::compare_exchange). Deletion is also quite trivial: We
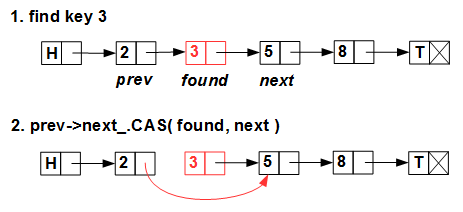
linearly look for the element to be deleted and atomically, with CAS, throw the pointer from its predecessor to the element following it.
The problems begin when all this is done together and in parallel: thread A deletes the element with key 3, thread B inserts key 4:

Streams A and B simultaneously search; at the same time, they remember in local variables the position found for deletion (A) and for insertion (B). Then thread A safely deleted 3 from the list, thread B at this time, for example, was
iprevand inextin the list — and it runs the atomic CAS primitive to insert the element - where? After the item with key 3, which is already excluded from the list! (Hazard Pointer / RCU guarantees that element 3 has not yet been physically deleted, that is, we will not get a “garbage treatment”, but 3 is already excluded from the list by thread A). Everything was done without errors, as a result, the element with the key 4 is lost and in addition we got a memory leak.T. Harris found an elegant solution to this problem in 2001. He proposed a two-phase deletion of an element: the first phase - logical deletion - marks the element as deleted, not excluding it from the list, the second phase - physical exclusion - excludes the element from the list (and the third phase - physical deletion - is performed by the safe memory deletion scheme - Hazard Pointer, RCU or similar). The meaning of logical deletion is to mark the element to be deleted so that CAS does not work on it . Harris suggested using the least significant bit of the pointer.
nextitem. Indeed, in modern architectures (both processors and the OS), the data is aligned on the border of 4 (for 32bit) or 8 (for 64bit) bytes, so the lower 2 or 3 bits of any pointer are always zero and can be used as bit flags. This trick got its own name marked pointer and is widely used in lock-free programming. Using marked pointer, parallel insertion / deletion looks like this:
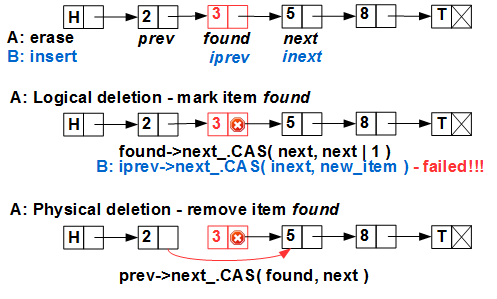
Stream A marks element 3 as logically deleted - sets the least significant bit of the pointer
found->nextto one. Now thread B, trying to insert 4 after 3, will fail - CAS will not work, since we believe that the pointer is 3.nextnot marked. The price of the marked pointer method is an additional CAS call when an item is deleted.
It may seem that all of the above is unnecessary and much faster and easier to just assign a
nextvalue to the pointer of the element to be deleted nullptr- then CAS on the insert will not work. Yes, it's easier, but these are two independent operations: one is an exception, the other is zeroing next. And if there are two operations, then someone can wedge between them and insert a new element after the already excluded one. Thus, we only reduce the probability of an error, but do not exclude it. Lock-free grimaces: everything should be done as atomically as possible, but in any case - without violating the internal structure of the container.Historical excursion
An interesting evolution of the Harris algorithm for the lock-free ordered list. The original algorithm is distinguished by the fact that for it, in principle, the Hazard Pointer scheme is not applicable. The fact is that Harris’s algorithm involves the physical removal of a chain of related list nodes, which is, in principle, endless. As we know, the Hazard Pointer scheme requires you to first protect deleted items by declaring them hazardous, and only then do something with them. But the number of hazard pointers is limited , we cannot protect the entire dimensionless chain of elements!
When developing Hazard Pointer, M.Michael revealed this fundamental inapplicability of his scheme to Harris' elegant algorithm and proposed his modification, which also uses two-phase deletion - receiving a marked pointer - but deletes elements one at a time , thereby making the use of Hazard Pointer permissible.
There is another modification of this algorithm that solves the problem of resuming the search.. As I have repeatedly emphasized, all lock-free algorithms are an endless cycle of “sweeping until it works out”. Describing the interesting situations above, I did not mention what needs to be done when CAS did not work. In fact, everything is simple: if the CAS on insertion / deletion did not work, we should again try to insert / delete from the very beginning - from the search for a position - until we either perform the operation or we realize that it is impossible to perform it (for insertion - because the key is already in the list, for deletion - because the key is not in the list). Resuming an operation from the beginning of the list is an expensive thing if the list is long (and we will see later that on the basis of the list described here you can build a rather efficient ordered container algorithm that supports millions of elements), so the thought comes up: But what if you start a second search not from the beginning, but from some previous element? But the concept of “previous” in the ever-changing world of lock-free is very shaky. Fomichev inhis dissertation suggests adding to each element of the lock-free list back-reference to some previous element and describes methods of working with these pointers and keeping them up to date, quite complicated.
Well, to the heap - there is an original algorithm for an ordered list based on fine-grained locks at the level of each element - lazy list . It is also implemented in libcds. Despite its lock-based nature, the hash map built on it is not much inferior to the lock-free counterpart discussed in this article. As mutexes, it uses spin-locks by default.
When developing Hazard Pointer, M.Michael revealed this fundamental inapplicability of his scheme to Harris' elegant algorithm and proposed his modification, which also uses two-phase deletion - receiving a marked pointer - but deletes elements one at a time , thereby making the use of Hazard Pointer permissible.
There is another modification of this algorithm that solves the problem of resuming the search.. As I have repeatedly emphasized, all lock-free algorithms are an endless cycle of “sweeping until it works out”. Describing the interesting situations above, I did not mention what needs to be done when CAS did not work. In fact, everything is simple: if the CAS on insertion / deletion did not work, we should again try to insert / delete from the very beginning - from the search for a position - until we either perform the operation or we realize that it is impossible to perform it (for insertion - because the key is already in the list, for deletion - because the key is not in the list). Resuming an operation from the beginning of the list is an expensive thing if the list is long (and we will see later that on the basis of the list described here you can build a rather efficient ordered container algorithm that supports millions of elements), so the thought comes up: But what if you start a second search not from the beginning, but from some previous element? But the concept of “previous” in the ever-changing world of lock-free is very shaky. Fomichev inhis dissertation suggests adding to each element of the lock-free list back-reference to some previous element and describes methods of working with these pointers and keeping them up to date, quite complicated.
Well, to the heap - there is an original algorithm for an ordered list based on fine-grained locks at the level of each element - lazy list . It is also implemented in libcds. Despite its lock-based nature, the hash map built on it is not much inferior to the lock-free counterpart discussed in this article. As mutexes, it uses spin-locks by default.
So, we have analyzed the lock-free algorithm of an ordered list, with which you can implement a lock-free hash map. The disadvantage of this algorithm is that it does not provide for rehashing, that is, we need to know a priori the estimated number of S elements in such a container and the optimal load factor. Then the size N of the hash table
T[N]is equal S / load factor. Nevertheless, despite these limitations, or rather, thanks to them, such an algorithm is one of the fastest and most scalable, since there is no overhead for rehashing.According to the results of my experiments, a good load factor is 2-4, that is, each lock-free list of collisions contains on average 2-4 elements. With load factor = 1 (the collision list consists of one element on average), the results are slightly better, but there is more memory overhead for actually degenerate collision lists.
In the next article, we will consider an algorithm that very originally supports rehashing and is based on the lock-free ordered list described here.
Lock-free data structures
