Crossword Puzzle Algorithm
This story begins with the publication “The Most Complex Computer-Generated Crossword Puzzle” . It contains one of the most complex crosswords compiled by the program (see below).

I was sure that all the crosswords were generated programmatically a long time ago and was somewhat surprised that this could be a problem. I note that we are talking about the "Canadian" crosswords, in which each word has an intersection with another word on each letter or very close to them in complexity. In my work, analytics, there are not many really complex tasks, so it became interesting for me to try to develop an algorithm that could do this. The result of reflection, supported by a program for generating crosswords, is given in this article.
To fill the crossword puzzle is always used brute force. We put the first word, then all the following, checking that the letters at the intersections coincide with the letters in the words set earlier. And so, until all the words are delivered. It would seem that there is nothing easier. However, simply counting the number of iterations of word matching for a crossword of average length by 50 words can change this opinion. So, to install any word except the first one, if there are 1,000 words of the corresponding length in the database and there is only one previously filled word at the intersection, on average 1,000/33 = 30 iterations will be needed (on average, we will need to look at 30 words before we come across a word having the desired letter at the position of the intersection filled earlier). If there is more than one previously filled intersection word, this number will increase sharply. A simple calculation shows that to fill 50 words, we need to do 30 ^ (50-1) iterations. These are billions of billions of iterations. Even on modern computers, it will require days and months of work. And here, the search itself is no longer in the first place, but an algorithm that will reduce the time it takes to generate a crossword puzzle by many orders of magnitude.
Immediately, "ashore", we must accept that the generation of the crossword puzzle will consist of two stages:
Based on this, I will mark the solutions given below, to which stage they are applicable.
All experiments will be performed on the crossword puzzle shown in the figure below.

This is not the most difficult crossword puzzle, but the solutions relevant to it will be relevant for all other crosswords. A small number of words guarantees us a relatively quick result.
And the last one. The article will omit everything related to the generation of the word base for the program. This part was “worth” at least 50% of the total time spent. Now the database has more than 158 thousand words, of which more than 125 thousand are unique. The base has been cleaned to the maximum extent programmatically, however, it still requires attention in manual mode. I did not in any way close or encrypt the database - it lies open in text form and in the simplest key-value format. You can delete or add words in it, correct the descriptions or completely replace it with your own (for example, in another language).
The first thing to determine is the sequence of filling in the words. There are very simple and obvious solutions for this.
Decision No. 1: Words will be generated in a sequence that depends primarily on their length. The longer the word, the more intersections it may have and the more difficult it will be to find the word to set. On the contrary, the shortest words, 2 or 3 letters long, will have a minimum number of intersections and it is most convenient to select them at the final stage of generation. This solution is used at the analysis stage.
Solution No. 2: Of the words with the same length, the words with the greatest difficulty of installation will be installed first. The complexity of the installation is a calculated parameter that shows "how difficult it will be to pick up the meaning in this word" and "how much will the price of error be if the word fails to pick up." It is clear that words of the same length, for example, 5 letters, can intersect either with one word or with five at once, while the complexity of the installation will be completely different. This solution is used at the analysis stage.
Decision No. 3: Based on the previous decisions, our words are arranged in such a sequence that does not guarantee the intersection of two neighboring words with each other. This means that if we did not find a word for installation, then we need to change not the previous word, but one of the previously installed words that intersect with this word and, in essence, set the selection conditions for it. It is logical from all previously established intersection words to replace the last word set to roll back to the minimum number of generation words. This solution is used at the generation stage.
If you trace the installation of words in the sequence that was determined on the basis of decisions No. 1 and No. 2, you will notice that the installation of some words forms locally independent fragments. Take a look at the picture below.
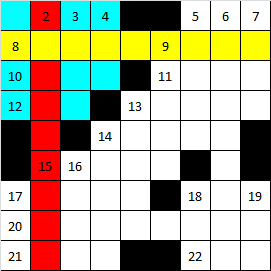
The color drawing shows the sequence of installing the first words in the crossword puzzle grid in the order corresponding to the well-known “Every hunter wants to know where the pheasant sits”. The first word to be set is red. After it is a word marked in yellow, etc. After installing only 2 words in a crossword puzzle, a local fragment formed, marked in blue.
Before continuing, we will first determine the terminology:
When a fragment appears, a dilemma arises - either continue to generate the crossword in a previously defined sequence, or first generate all the words in the fragment in order to verify that the start word is correctly set. This is one of the places in the algorithm that can critically affect its overall performance and which does not have a clear logical solution.
Solution No. 4: For each word that is set, fragments will be searched. All words belonging to one fragment will have a sequential order of installation, starting from the start word, or from the first word of the fragment. This solution is used at the analysis stage.
At the moment, part of the algorithm for changing the sequence of generating words of fragments is as follows:
Actually that's all - the algorithm for generating a crossword puzzle by ordinary enumeration is ready. With minimal detail, it looks like this:
Checked - it really works on grids up to medium difficulty. However, as the crossword puzzle grid becomes more complex and the number of words increases, the number of successful generation attempts tends to 0. Actually, from this moment the most interesting begins.
The first question that comes to mind is: is it possible to somehow reduce the number of rollbacks? After all, each rollback a few words back can cost tens and hundreds of thousands of iterations. The logical step is to add rules that reduce the number of installation errors for words, such as not putting a soft or hard sign in the cell with which the word begins, etc. If you do not go deep, to describe most of these rules for the Russian language is quite simple, but there is a problem - they will be absolutely useless, for example, for English. I wanted to make a universal algorithm, independent of the language.
Reflections on this issue led to the following: “it would be good if, for each word that is still unidentified, crossing the current word to be installed, the availability of installation options is guaranteed.”
So the idea came up to use templates similar to the LIKE command in Transact-SQL. A pattern is a character string that will be used to compare words. The template itself includes letters and wildcards. When comparing with a pattern, it is necessary that the letters exactly match the characters indicated on the line. Pattern characters can match arbitrary elements of a character string.
Decision No. 5: For each starting word, patterns of all words intersecting with it will be calculated. The starting word must have letters strictly from the list in the template corresponding to the position of the intersection letter. This solution is used at the generation stage.
Examples of patterns for three-letter words are given below:
Using the latter as an example, you should read the patterns as follows: for a word of 3 letters whose first two letters are equal to "DO", there are words in the database whose last letter is equal to one of "G K M N".
Let's go back to the fragments. Take a look at the picture below.
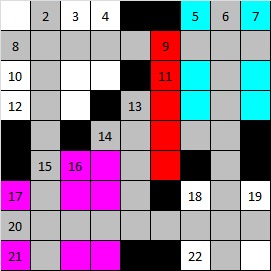
In it gray cells of the words established earlier are marked. When setting the word marked in red, two fragments are formed at once, marked with blue and violet colors.
If you look at the purple fragment, you will see that it is associated with the start word with one single intersection. And this is wonderful! This gives us the opportunity to use another solution.
A little more terminology:
Solution No. 6: If the fragment for which the start word is an accelerator is unsuccessful, the algorithm will store a list of letters that were installed in the start word at the intersection with one of the words of the fragment to block re-setting of words with these letters at the said intersection. This solution is used at the generation stage.
The algorithm for using accelerators is given below.
First, how it works without an accelerator:
The fragment depth can be large enough and the total number of iterations to fill the fragment can be in the millions. To sort through all possible options, you need the number of iterations for a single filling of a fragment, multiply by the number of words in the database with a length, like a start word (which can be tens of thousands).
How it works with the accelerator:
The depth of the fragment is the same. However, to sort through all possible options, you need to multiply the number of iterations to fill the fragment not by the number of options for the starting word, but by only 33 (the number of letters in the alphabet).
Previous decisions, in fact, have exhausted those 20% of the efforts that, according to the Pareto principle, give us 80% of the result. Then we have to use more and more complex approaches, with sometimes unclear prospects.
Once, when generating a crossword puzzle, the program issued the following message: "Time for exhaustive search: 11,471 days ...". This message appears only if all variants for the very first word have been enumerated and a new meaning is to be found for it. The program already spent time simply multiplies by the remaining number of options. This amused me and made me wonder if this time can be converted into a result? The idea is to deliberately trim some search options that have a minimal chance of success.
The main thesis of this decision is that it is better if the program yields a negative result in the shortest possible time (that is, among the most optimal options the selection failed) than it will engage in the selection for so long that all conceivable boundaries will be exceeded.
Decision No. 7: When installing a word that intersects words with great difficulty of installation, it is forbidden to put letters at the position of the mentioned intersection, the frequency of use of which in word intersections is minimal. This solution is used at the generation stage.
If for simple reasons, this solution discards a certain number of letters of the Russian alphabet (sometimes up to 20), increasing the chance to generate complex sections from words with more frequently used letters (here the Italian alphabet is in chocolate with its 21 letters). As a result, we will get more options for selecting a difficult-to-install word when it comes to the turn, which means there is a greater chance for the successful generation of the entire crossword puzzle.
There are also disadvantages - some of the search options will be irretrievably lost. Perhaps, among them will be the very, only possible option of filling the grid. Only you can get it in 30 years - you just have to wait a bit.
Another disadvantage is that long words with more than 10 intersections are blocked the most. This leads to the fact that the program can not start the generation by blocking the first word until it runs out of options. This minus is only partially bypassed, by reducing the degree of blocking, and hence the effectiveness of this solution.
To organize the grids according to the complexity of generation, the attribute “Complexity of generation” is introduced, which is calculated based on the number of words, their length and the number of intersections. In fact - a less stable result can be obtained with complexity up to 600 units. All of the above is for luck.
Below is the average generation time for 10 attempts for several grids arranged in increasing order of generation complexity.

A simple test grid for experiments, with a small number of words.
Subtotal: Grids of such complexity are generated quickly and stably.

This grid is more complicated. This is a small “Canadian” crossword, where all words have intersections in all letters.
Subtotal: Grids of such complexity in most cases are generated quite quickly, however, sometimes the generation can drag on for 10 minutes or more.

This rather complicated grid turned out to be very “convenient” for generation.
Subtotal: Due to the fact that this grid is very well fragmented and intersections are not found on all letters of long words, the program generates it almost instantly.

But this grid already has a “target” complexity. This is a full-fledged “Canadian” crossword puzzle, however, far from the most difficult.
Subtotal: The program did it! A successful generation result, in the most extreme case, can be obtained in just 17 minutes. The average generation time is just over 4 minutes.

And finally, the most complicated crossword puzzle that started it all. It has 72 words, which is not so much. However, the complexity of the generation turned out to be very high. The main problem for generating are the four longest words, with which almost all other words of the crossword cross. They are like skeleton bones, on which you need to string all the other words. Rollbacks are thrown away by the generation process almost to the very beginning. Thus, the process of generating this grid can be compared with Sisyphus, pushing a stone uphill. And every time when there is very little left to the goal, the stone rolls down to the very beginning of the path.
Alas - this peak remained unconquered! I started several generations with different settings, with a limit of up to 10 hours, however, none of them were completed successfully. There is clearly not enough time. Who knows, maybe this unconquered peak will inspire someone to a new assault!
And yet yes! Generating a crossword puzzle, even for the most modern computers, is a daunting task. I am sure that the possibilities to improve this algorithm are far from exhausted, however, regardless of the capabilities of the algorithm and the power of the computer, you can always complicate the crossword puzzle grid a little more so that the program will promise you the result, in 20-30 years.
I hope you were interested, and you read to the end.

I was sure that all the crosswords were generated programmatically a long time ago and was somewhat surprised that this could be a problem. I note that we are talking about the "Canadian" crosswords, in which each word has an intersection with another word on each letter or very close to them in complexity. In my work, analytics, there are not many really complex tasks, so it became interesting for me to try to develop an algorithm that could do this. The result of reflection, supported by a program for generating crosswords, is given in this article.
To fill the crossword puzzle is always used brute force. We put the first word, then all the following, checking that the letters at the intersections coincide with the letters in the words set earlier. And so, until all the words are delivered. It would seem that there is nothing easier. However, simply counting the number of iterations of word matching for a crossword of average length by 50 words can change this opinion. So, to install any word except the first one, if there are 1,000 words of the corresponding length in the database and there is only one previously filled word at the intersection, on average 1,000/33 = 30 iterations will be needed (on average, we will need to look at 30 words before we come across a word having the desired letter at the position of the intersection filled earlier). If there is more than one previously filled intersection word, this number will increase sharply. A simple calculation shows that to fill 50 words, we need to do 30 ^ (50-1) iterations. These are billions of billions of iterations. Even on modern computers, it will require days and months of work. And here, the search itself is no longer in the first place, but an algorithm that will reduce the time it takes to generate a crossword puzzle by many orders of magnitude.
To the track ...
Immediately, "ashore", we must accept that the generation of the crossword puzzle will consist of two stages:
- Analysis - creating a generation plan, the main result of which is a certain sequence of generating crossword words and other data that will help at the generation stage.
- Generation - the sequential filling of the crossword puzzle grid with words, by the method of exhaustive search of all possible options, taking into account the data obtained at the stage of analysis.
Based on this, I will mark the solutions given below, to which stage they are applicable.
All experiments will be performed on the crossword puzzle shown in the figure below.

This is not the most difficult crossword puzzle, but the solutions relevant to it will be relevant for all other crosswords. A small number of words guarantees us a relatively quick result.
And the last one. The article will omit everything related to the generation of the word base for the program. This part was “worth” at least 50% of the total time spent. Now the database has more than 158 thousand words, of which more than 125 thousand are unique. The base has been cleaned to the maximum extent programmatically, however, it still requires attention in manual mode. I did not in any way close or encrypt the database - it lies open in text form and in the simplest key-value format. You can delete or add words in it, correct the descriptions or completely replace it with your own (for example, in another language).
The beginning of the way
The first thing to determine is the sequence of filling in the words. There are very simple and obvious solutions for this.
Decision No. 1: Words will be generated in a sequence that depends primarily on their length. The longer the word, the more intersections it may have and the more difficult it will be to find the word to set. On the contrary, the shortest words, 2 or 3 letters long, will have a minimum number of intersections and it is most convenient to select them at the final stage of generation. This solution is used at the analysis stage.
Solution No. 2: Of the words with the same length, the words with the greatest difficulty of installation will be installed first. The complexity of the installation is a calculated parameter that shows "how difficult it will be to pick up the meaning in this word" and "how much will the price of error be if the word fails to pick up." It is clear that words of the same length, for example, 5 letters, can intersect either with one word or with five at once, while the complexity of the installation will be completely different. This solution is used at the analysis stage.
Decision No. 3: Based on the previous decisions, our words are arranged in such a sequence that does not guarantee the intersection of two neighboring words with each other. This means that if we did not find a word for installation, then we need to change not the previous word, but one of the previously installed words that intersect with this word and, in essence, set the selection conditions for it. It is logical from all previously established intersection words to replace the last word set to roll back to the minimum number of generation words. This solution is used at the generation stage.
Fragments
If you trace the installation of words in the sequence that was determined on the basis of decisions No. 1 and No. 2, you will notice that the installation of some words forms locally independent fragments. Take a look at the picture below.

The color drawing shows the sequence of installing the first words in the crossword puzzle grid in the order corresponding to the well-known “Every hunter wants to know where the pheasant sits”. The first word to be set is red. After it is a word marked in yellow, etc. After installing only 2 words in a crossword puzzle, a local fragment formed, marked in blue.
Before continuing, we will first determine the terminology:
- A fragment is a group of words in the amount of from 1 word to 50% of the total number of words in the crossword puzzle, the generation of which does not depend on all the remaining, not yet set words.
- The start word is the word after the installation of which a fragment was formed (in the figure above it is the word highlighted in yellow).
- The first word is the fragment word, which has the lowest order of installation of all words in the fragment.
- Fragment Depth - the number of words that make up the fragment.
When a fragment appears, a dilemma arises - either continue to generate the crossword in a previously defined sequence, or first generate all the words in the fragment in order to verify that the start word is correctly set. This is one of the places in the algorithm that can critically affect its overall performance and which does not have a clear logical solution.
Solution No. 4: For each word that is set, fragments will be searched. All words belonging to one fragment will have a sequential order of installation, starting from the start word, or from the first word of the fragment. This solution is used at the analysis stage.
At the moment, part of the algorithm for changing the sequence of generating words of fragments is as follows:
- Find the fragments.
- We determine the complexity of filling the fragment.
- We determine the word, after which it is necessary to arrange all the words of the fragment according to the following rules:
- Words that are members of fragments, set one after another.
Actually that's all - the algorithm for generating a crossword puzzle by ordinary enumeration is ready. With minimal detail, it looks like this:
- The sequence of word generation is determined.
- The selection and installation of the word is carried out taking into account previously installed words.
- If there is no word for installation, a rollback is performed to the last word intersecting with it, the search of which continues as if its previous value was not found at all.
Checked - it really works on grids up to medium difficulty. However, as the crossword puzzle grid becomes more complex and the number of words increases, the number of successful generation attempts tends to 0. Actually, from this moment the most interesting begins.
Patterns
The first question that comes to mind is: is it possible to somehow reduce the number of rollbacks? After all, each rollback a few words back can cost tens and hundreds of thousands of iterations. The logical step is to add rules that reduce the number of installation errors for words, such as not putting a soft or hard sign in the cell with which the word begins, etc. If you do not go deep, to describe most of these rules for the Russian language is quite simple, but there is a problem - they will be absolutely useless, for example, for English. I wanted to make a universal algorithm, independent of the language.
Reflections on this issue led to the following: “it would be good if, for each word that is still unidentified, crossing the current word to be installed, the availability of installation options is guaranteed.”
So the idea came up to use templates similar to the LIKE command in Transact-SQL. A pattern is a character string that will be used to compare words. The template itself includes letters and wildcards. When comparing with a pattern, it is necessary that the letters exactly match the characters indicated on the line. Pattern characters can match arbitrary elements of a character string.
Decision No. 5: For each starting word, patterns of all words intersecting with it will be calculated. The starting word must have letters strictly from the list in the template corresponding to the position of the intersection letter. This solution is used at the generation stage.
Examples of patterns for three-letter words are given below:
- Template: "___"
- Letter No. 1: А A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
- Letter No. 2: Y A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
- Letter No. 3: Y A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
- Template: "TO_"
- Letter No. 1: D
- Letter number 2: O
- Letter No. 3: G K M N
Using the latter as an example, you should read the patterns as follows: for a word of 3 letters whose first two letters are equal to "DO", there are words in the database whose last letter is equal to one of "G K M N".
Accelerators
Let's go back to the fragments. Take a look at the picture below.

In it gray cells of the words established earlier are marked. When setting the word marked in red, two fragments are formed at once, marked with blue and violet colors.
If you look at the purple fragment, you will see that it is associated with the start word with one single intersection. And this is wonderful! This gives us the opportunity to use another solution.
A little more terminology:
- Accelerator - a start word that has a child fragment, having one single intersection with it. He got his name for the property to accelerate the generation of fragments by an order of magnitude or more.
Solution No. 6: If the fragment for which the start word is an accelerator is unsuccessful, the algorithm will store a list of letters that were installed in the start word at the intersection with one of the words of the fragment to block re-setting of words with these letters at the said intersection. This solution is used at the generation stage.
The algorithm for using accelerators is given below.
First, how it works without an accelerator:
- Search and installation of all words of the fragment is performed.
- If the filling of the fragment is successful, then move on, otherwise - the starting word changes and the process of filling in the words of the fragment is repeated.
The fragment depth can be large enough and the total number of iterations to fill the fragment can be in the millions. To sort through all possible options, you need the number of iterations for a single filling of a fragment, multiply by the number of words in the database with a length, like a start word (which can be tens of thousands).
How it works with the accelerator:
- Searches and sets the words for the fragment.
- If the filling of the fragment is successful, then go ahead, otherwise - remember the letter at the intersection of the accelerator and the word of the fragment.
- The word installed on the accelerator changes, while the new word should not have letters that were previously remembered at the intersection mentioned above.
The depth of the fragment is the same. However, to sort through all possible options, you need to multiply the number of iterations to fill the fragment not by the number of options for the starting word, but by only 33 (the number of letters in the alphabet).
Dynamic balancing of installation complexity
Previous decisions, in fact, have exhausted those 20% of the efforts that, according to the Pareto principle, give us 80% of the result. Then we have to use more and more complex approaches, with sometimes unclear prospects.
Once, when generating a crossword puzzle, the program issued the following message: "Time for exhaustive search: 11,471 days ...". This message appears only if all variants for the very first word have been enumerated and a new meaning is to be found for it. The program already spent time simply multiplies by the remaining number of options. This amused me and made me wonder if this time can be converted into a result? The idea is to deliberately trim some search options that have a minimal chance of success.
The main thesis of this decision is that it is better if the program yields a negative result in the shortest possible time (that is, among the most optimal options the selection failed) than it will engage in the selection for so long that all conceivable boundaries will be exceeded.
Decision No. 7: When installing a word that intersects words with great difficulty of installation, it is forbidden to put letters at the position of the mentioned intersection, the frequency of use of which in word intersections is minimal. This solution is used at the generation stage.
If for simple reasons, this solution discards a certain number of letters of the Russian alphabet (sometimes up to 20), increasing the chance to generate complex sections from words with more frequently used letters (here the Italian alphabet is in chocolate with its 21 letters). As a result, we will get more options for selecting a difficult-to-install word when it comes to the turn, which means there is a greater chance for the successful generation of the entire crossword puzzle.
There are also disadvantages - some of the search options will be irretrievably lost. Perhaps, among them will be the very, only possible option of filling the grid. Only you can get it in 30 years - you just have to wait a bit.
Another disadvantage is that long words with more than 10 intersections are blocked the most. This leads to the fact that the program can not start the generation by blocking the first word until it runs out of options. This minus is only partially bypassed, by reducing the degree of blocking, and hence the effectiveness of this solution.
Testing
To organize the grids according to the complexity of generation, the attribute “Complexity of generation” is introduced, which is calculated based on the number of words, their length and the number of intersections. In fact - a less stable result can be obtained with complexity up to 600 units. All of the above is for luck.
Below is the average generation time for 10 attempts for several grids arranged in increasing order of generation complexity.
Grid No. 1

A simple test grid for experiments, with a small number of words.
- Generation Difficulty: 248
- Word Count: 28
- Average time of successful generation, sec .: 5 (from 1 to 32)
Subtotal: Grids of such complexity are generated quickly and stably.
Grid No. 2

This grid is more complicated. This is a small “Canadian” crossword, where all words have intersections in all letters.
- Generation Difficulty: 372
- Word Count: 34
- Average time of successful generation, sec .: 62 (from 1 to 472)
Subtotal: Grids of such complexity in most cases are generated quite quickly, however, sometimes the generation can drag on for 10 minutes or more.
Grid No. 3

This rather complicated grid turned out to be very “convenient” for generation.
- Generation Difficulty: 544
- Word Count: 46
- Average time of successful generation, sec .: 1 (from 1 to 2)
Subtotal: Due to the fact that this grid is very well fragmented and intersections are not found on all letters of long words, the program generates it almost instantly.
Net No. 4

But this grid already has a “target” complexity. This is a full-fledged “Canadian” crossword puzzle, however, far from the most difficult.
- Generation Difficulty: 570
- Word Count: 78
- Average time of successful generation, sec .: 250 (from 10 to 989)
Subtotal: The program did it! A successful generation result, in the most extreme case, can be obtained in just 17 minutes. The average generation time is just over 4 minutes.
Grid No. 5

And finally, the most complicated crossword puzzle that started it all. It has 72 words, which is not so much. However, the complexity of the generation turned out to be very high. The main problem for generating are the four longest words, with which almost all other words of the crossword cross. They are like skeleton bones, on which you need to string all the other words. Rollbacks are thrown away by the generation process almost to the very beginning. Thus, the process of generating this grid can be compared with Sisyphus, pushing a stone uphill. And every time when there is very little left to the goal, the stone rolls down to the very beginning of the path.
Alas - this peak remained unconquered! I started several generations with different settings, with a limit of up to 10 hours, however, none of them were completed successfully. There is clearly not enough time. Who knows, maybe this unconquered peak will inspire someone to a new assault!
Summary
And yet yes! Generating a crossword puzzle, even for the most modern computers, is a daunting task. I am sure that the possibilities to improve this algorithm are far from exhausted, however, regardless of the capabilities of the algorithm and the power of the computer, you can always complicate the crossword puzzle grid a little more so that the program will promise you the result, in 20-30 years.
I hope you were interested, and you read to the end.
