Automatic age rating system for facial images
- Transfer
Abstract
People are the most important tracking objects in video surveillance systems. However, tracking a person alone does not provide sufficient information about his motives, intentions, desires, etc. In this work, we present a new and reliable system for automatic age estimation using computer vision technology. It uses global facial features obtained by combining Gabor wavelets and preserving the orthogonality of local projections Orthogonal Locality Preserving Projections, OLPP). In addition, the system is capable of estimating age from real-time images. This means that the proposed system has greater potential compared to other semi-automatic systems. The results obtained in the application of the proposed approach can provide a clearer understanding of the algorithms in the field of age estimation necessary for developing applications relevant for real applications.
Keywords: Gabor wavelets, face image, age estimation, support vector machine ( Support Vector Machine , SVM).
1. Introduction
The image of a human face contains abundant information about a person, including facial features, emotions, gender, age, etc. In general, an image of a person’s face can be considered as a complex signal, consisting of many face properties, such as: skin color, geometric features of facial features . These attributes play an important role in real face image analysis applications. In such applications, various properties (attributes) evaluated from the captured face image can be used for further reaction (actions) of the system. Age, in particular, is one of the most important attributes. For example, users may require an age-dependent interactive computer system, or a system that can estimate age to provide access control, or a system for collecting intelligence.
The automatic age estimation system consists of two parts: face detection in the image and the age estimate itself. It is quite difficult to detect faces in the image, because the detection results are highly dependent on many conditions: environment, movement, lighting, orientation of faces in space, expression of emotions. These factors can lead to distortions in the color, brightness, shadows, and contours of images. For this reason, Viola and Jones proposed their famous face detection system in 2004. The Viola-Jones classifier uses the AdaBoost algorithm at each node of the classifier cascade to train a high degree of face detection by reducing the number of faces ignored throughout the cascade. This algorithm has the following features: 1) uses Haar features- comparison of differences in the sums of intensities of pixels in two rectangular areas with threshold values; 2) the use of an integrated image to accelerate the calculation of the sums of pixels in a rectangular region or a rectangular region rotated by an angle of 45 degrees; 3) the AdaBoost algorithm uses statistical boosting to create binary (face - not face) classification nodes characterized by a good probability of detecting faces and a low probability of missing a face; 4) nodes of weak classifiers are organized in a cascade with the aim of eliminating non-face images at the initial stage of the algorithm (i.e., the first levels of the cascade allow more errors of incorrect classification, but work faster than the subsequent levels of the cascade classifier). A person is classified as a person
Although automatic detection of faces in an image is a mature technique involving many applications, estimating age from a face image is still a difficult task. This is because the aging process is expressed differently, not only among different races, but also within the race. This process is mostly personal. In addition, it is also determined by the influence of external factors: lifestyle (proper nutrition, sport), place of residence, weather conditions. Therefore, the issue of sustainable age estimates is an open problem.
In general, there are three categories of feature extraction methods for assessing a person’s age in the literature. The first category is statistical approaches. Xin Geng et al. [2, 3] proposed AGing pattErn Subspace (AGES), a method for automatic age estimation. The idea of this approach is to model the pattern (pattern) of aging, which is determined by the sequence of personal images of facial aging. This model is built by studying subspace like an EM iterative learning method for principal components analysis (PCA). In other works [4, 5], Guodong Guo et al. Compare three typical methods for reducing dimensions of feature spaces and various embedding methods such as: PCA, locally linear embedding (Locally Linear Embedding (LLE), Orthogonal Locality Preserving Projections (OLPP). According to the distribution of data in the OLPP subspace, they offer the Locally Adjusted Robust Regression (LARR) method for training and predicting a person’s age. LARR uses Support Vector Regression (SVR) for rough prediction and determines local settings within a small limited range of ages centered on the result using the Support Vector Machine (SVM) method .
The second category of methods includes an approach based on the Active Appearance Model (AAM). Using the appearance model is the most intuitive method among all face image analysis methods.
Young H. Kwon et al. [6] used visual age features to construct an anthropometric model. Primary features are the eyes, nose, mouth and chin. The relations of these features were calculated to distinguish between different age categories. When analyzing secondary features, a wrinkle map was used to control the detection and measurement of wrinkles. Jun ‐ Da Txia et al. [7] proposed an age estimation method based on the active appearance model(AAM) for extracting regions of age-specific features. Each face requires the calculation of 28 special points and is divided into 10 regions of wrinkles. Shuicheng Yan et al. [8] used a path-based appearance model called Patch-Kernel. This method is designed to determine the Kullback-Leibler distance between models that are derived from the global model of Gaussian mixtures (GMM) using the maximum a Posteriori probability ( MAP) of any two images. The ability to classify was then enhanced by the use of a weak learning process called intermodal similarity synchronization. Nuclear regression is used at the end to estimate age.
The third category of methods uses a frequency-based approach. In image processing and pattern recognition, frequency domain analysis is one of the most popular methods for extracting image features. Guodong Guo et al. [9] investigated the "biological" image features ( biologically inspired features , BIF) to estimate the age of people image. Unlike previous works [4, 5], Guo modeled a person’s face using Gabor filters [10]. Gabor filters are linear filters used in image processing to highlight the boundaries of objects within an image. The frequency and orientation of the Gabor filter representations is similar to human vision and is well suited for texture representation and solving the discrimination problem.
Our system uses cascaded AdaBoost for training for face detection, and receives an estimate of age through the use of Gabor and OLPP wavelets. This article consists of the following sections. The first includes a description of the face detection system: histogram alignment, feature selection, cascading classifier, trained AdaBoost and the algorithm for clustering regions of the face image. The second section: the process of assessing age includes extracting features using Gabor wavelets, sifting out features and choosing the best, classifying the age. At the end of the article, the simulation results and conclusions are drawn.
This article proposes a fully automatic age rating system that uses Gabor wavelets to represent the aging process. The system we offer has 4 main modules: 1) face detection; 2) analysis based on Gabor wavelets; 3) OLPP reduction; 4) classification by the method of support vectors. The input image can come from the camera or read from a file. The face image is selected from the original image using the face detector using the approach described in [12]. Then the image is scaled to have a size of 64 * 64 pixels. Then, using 40 Gabor wavelet cores, features are extracted and OLPP reduction is applied to them. In the end, an age assessment is started using the trained SVM classifier.
The rest of the article is organized as follows: Section 2 describes the face detection subsystem using AdaBoost. Section 3 describes the age estimation algorithm and includes: texture analysis by Gabor wavelets, OLPP reduction, and SVM classification. Section 4 presents experimental results. Section 5 draws conclusions on the proposed system.
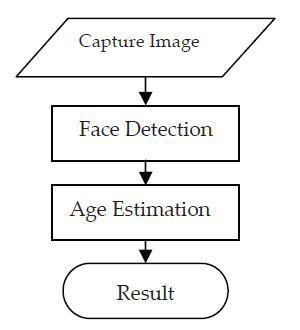
Figure 1. System Overview
2. Face Detection
Figure 1 shows the architecture of the automatic age estimation system proposed in our work. The whole system consists of a face detection subsystem, the task of which is to detect areas of faces in the image and age estimation subsystems. To search for faces in the image, scanning windows of various sizes are used, because when capturing an image, the object may be at different distances from the camera. There are a total of 12 scale levels of scanning, and the image size changes starting from 24 * 24 with a scale factor of 1.25. Depending on the lighting conditions in which the image is captured, there may be various variations in the brightness of the images. The image can be more accurately recognized (more precisely, the face in the image) after normalizing its brightness.
2.1. Normalization of illumination
Normalization of illumination is based on the method of alignment (adjustment) of histograms. The primary task of fitting the histograms is to convert the original histogram H (l) to the target histogram G (l). The target histogram G (l) is selected as the image histogram close to the average histogram for the face database. Select the target image and the histogram G (l) as shown in Figure 2 (a). Images before and after normalization are shown in Figures 2 (b) -.

Figure 2. Normalization of illumination. (a) Target image. (b) Input images. (c) Normalized images
Input images that are too dark or too light are normalized according to the histogram of the target image. The histograms H (l) are converted to the histograms G (l) as follows:
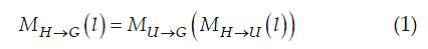
where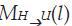 and
and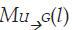 - direct and inverse mapping of histograms H (l) and G (l) into histograms of homogeneous (uniform) distributions.
- direct and inverse mapping of histograms H (l) and G (l) into histograms of homogeneous (uniform) distributions.
2.2 Selection of features
We have selected four rectangular Haar features as shown in Figure 3 [13].

Figure 3. Four types of rectangular features
It is permissible to use a composition of rectangles of different brightness to represent light and dark regions of the image. Features are defined as follows:
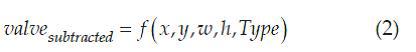
where (x, y) denotes the center of the relative coordinate system of the rectangular feature in the scanning window. The importance of w and h denotes the relative width and height of the rectangular feature, respectively. Type - type of rectangular feature, - the difference of the sums of pixels in the light and dark areas.
- the difference of the sums of pixels in the light and dark areas.
A rectangular feature that can effectively separate faces from non-faces is considered a weak classifier:

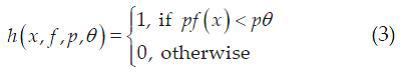
A weak classifier is used to determine if the current part of the image is a face or not a face based on counting a rectangular feature, threshold q, and polarity (direction of inequality) p. For each weak classifier, the optimal threshold is chosen so as to minimize the error of incorrect classification. The threshold is selected by training on a sample of 4000 face images and 59000 non-face images. Figures 4 (a) - (b) are examples from databases of individuals and non-individuals. In this procedure, we calculate the distribution of each feature
used to determine if the current part of the image is a face or not a face based on counting a rectangular feature, threshold q, and polarity (direction of inequality) p. For each weak classifier, the optimal threshold is chosen so as to minimize the error of incorrect classification. The threshold is selected by training on a sample of 4000 face images and 59000 non-face images. Figures 4 (a) - (b) are examples from databases of individuals and non-individuals. In this procedure, we calculate the distribution of each feature for each image in the database, and select a threshold that has the maximum discriminative ability (i.e. breaks the image into two classes better than the rest).
for each image in the database, and select a threshold that has the maximum discriminative ability (i.e. breaks the image into two classes better than the rest).

Figure 4. Database of faces (a) and non-faces (b)
Although each rectangular feature is calculated very efficiently, calculating all combinations is very computationally expensive. For example, for the smallest sliding window (24 * 24), the full set of features is 160,000.
The AdaBoost algorithm combines a set of weak classifiers to form a strong classifier. Although a strong classifier is effective for face detection applications, it has been running for quite some time. The cascading classifier structure, which improves detection ability and reduces computation time, was proposed by Viola and Jones [14]. Based on this idea, our cascading AdaBoost forms a strong classifier. In the first step, if the image from the sliding window is classified as a face, then we go to step 2, in another case, the image is discarded. A similar process is performed for all steps. The number of steps should be sufficient to achieve a good degree of recognition and at the same time, should minimize the computation time. For example, if at each step the probability of detecting a face is 0.99, The 10-step classifier will reach a probability of 0.9 (since 0.9 ~ = 0.99 ^ 10). Although achieving this probability may sound like a very difficult task, it can be done easily, since each step should have a false positive recognition error value of only about 30%.
The operation procedure of the AdaBoost algorithm can be described as follows: if m and l are the numbers of persons and non-persons, respectively, and j is the sum of non-persons and persons. The initial weights w_ (i, j) for the ith step can be defined as . The normalized weighted error of a weak classifier can be expressed as follows:
. The normalized weighted error of a weak classifier can be expressed as follows:
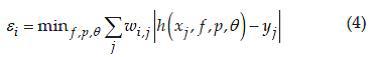
Weights are updated according to formula (5) in each iteration. If the object is classified correctly, then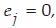 in the remaining cases ej = 1.
in the remaining cases ej = 1.
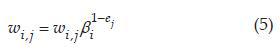
The final classifier for the i-th step is defined below:

where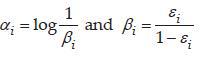
2.3 Area-based clustering
A face detector usually finds more than one face, even if it has one face (as shown in Figure 5).

Figure 5. The results of the face detector
Therefore, area-based clustering is used to solve this problem. The proposed method consists of two levels of clustering - local and global clustering. Local clustering is used to cluster blocks on a single scale and form a simple filter to determine the number of image blocks within clusters. If the number of blocks in a cluster is more than one, then this cluster is marked as probably containing a person, otherwise, the cluster is rejected. The local clustering method also has the following rule for deciding on cluster
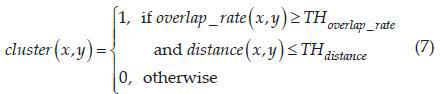
labeling : In formula (7), the percentage of overlap (x, y) denotes the distance between two detected candidate regions and is equal to the distance between the centers of these regions. Equality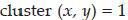 means that x and y are in the same cluster and these regions almost completely overlap each other
means that x and y are in the same cluster and these regions almost completely overlap each other
Figure 6 shows several possible cases of overlapping regions.

Figure 6. Diagrams of overlapping regions and distance of block centers
In Figure 6 (a), two blocks fall into one cluster. In Figure 6 (b), two blocks fall into different clusters, because the distance between their centers is greater than the threshold. For special cases, as shown in Figure 6 (c), all blocks are considered as candidates, but most of them are false faces. Therefore, in this work, for practical applications, we select only one block that satisfies equation (7) rather than several blocks. In the end, global clustering will use the blocks obtained during the local clustering stage, and the label of the facial region corresponds to the average size of all available blocks. Some results of the entire clustering process based on the choice of regions for the local and global levels are shown in Figure 7. From the right image in Figure 7, in fact,

Figure 7. Clustering results. (a) Local clustering results. (b) Global Clustering Results
3. Age Estimation
There are three main parts of our age rating system presented in this work: extracting age features, reducing the number of features, and classifying features. Feature extraction is performed using Gabor wavelets, which are used to analyze images because of their biological significance and computational properties. Gabor wavelet kernels are similar to the 2D perception of milk bacteria and expressing powerful spatial orientation and selectivity abilities, as well as being locally optimal in the spatial and frequency domains. Gabor transformation is well known, especially suitable for decomposition of images and their presentation, when the goal is the choice of local and distinctive features. Moreover, Donato and others [15] showed experimentally, that the representation through Gabor wavelets is effective for classifying facial features. This section introduces the basics of Gabor wavelets to represent the features of images and describes the reduction in the number of features, their selection into a vector used to estimate age.
3.1 Extraction of features using wavelets Gabor
Wavelet Gabor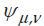 can be defined as follows [16]:
can be defined as follows [16]:
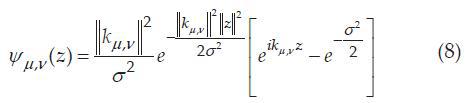
where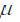 and
and 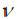 determine the orientation and scale Gabor kernel
determine the orientation and scale Gabor kernel  denotes an operator of calculating the norm, and the wave vector
denotes an operator of calculating the norm, and the wave vector  is defined as follows:
is defined as follows:

where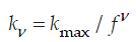 and
and  - the maximum frequency, and f - spatial factor between cores in the frequency domain. In general, the Gabor wavelet kernels in (8) are self-similar, since they can be derived from one filter, the mother wavelet, by scaling and rotation using the wave vector
- the maximum frequency, and f - spatial factor between cores in the frequency domain. In general, the Gabor wavelet kernels in (8) are self-similar, since they can be derived from one filter, the mother wavelet, by scaling and rotation using the wave vector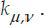 Each core is a product of a Gaussian convolution and a complex wave plane, while the first term in square brackets in (9) defines the vibrational part of the core, and the second term compensates for the direct current value. The sigma parameter is the standard deviation of the width of the Gaussian convolution from the wavelength.
Each core is a product of a Gaussian convolution and a complex wave plane, while the first term in square brackets in (9) defines the vibrational part of the core, and the second term compensates for the direct current value. The sigma parameter is the standard deviation of the width of the Gaussian convolution from the wavelength.
In most cases, researchers use Gabor wavelets with five different scales, and eight orientations.
and eight orientations.  Figure 8 shows the real part of Gabor cores at 5 scale levels and 8 directions, as well as their values for the following parameters:
Figure 8 shows the real part of Gabor cores at 5 scale levels and 8 directions, as well as their values for the following parameters: 
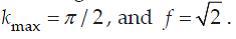

Figure 8. Representation of Gabor
wavelets Representation of wavelets Gabor for an image is a convolution of an image with a family of Gabor kernels using equation (8). Let be - distribution of gray image levels. The result of the convolution of image I
- distribution of gray image levels. The result of the convolution of image I 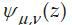 is defined as:
is defined as:
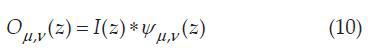
where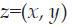 and * denotes the operator of convolution (convolution).
and * denotes the operator of convolution (convolution).
Using the convolution theorem, the fast Fourier transform (FFT) is used to obtain the result of the convolution operation. Equations (11) and (12) are the definition of convolution through FFT.
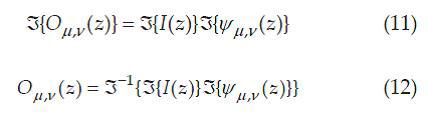
where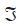 and
and 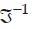 denote the Fourier transform and the inverse Fourier transform, respectively.
denote the Fourier transform and the inverse Fourier transform, respectively.

Figure 9. One of the sampled images and 40 outputs of the convolution operation
Figure 9 shows the output values of the convolution operations for the sample image. In accordance with Figure 9, the output convolution values exhibit spatial orientation and selectivity. Such characteristics produce robust local features that are suitable for visual recognition. Further, we denote the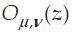 value of the outputs of the convolution operation.
value of the outputs of the convolution operation.
3.2 Reducing the number of features according to the scheme
In general, MGCs or other algorithms work with features in the form of Gabor wavelets to reduce the dimension of the converted data [19, 20]. Convolution results, corresponding to all Gabor wavelets, are brought together as a whole, and in order to improve computational efficiency, MGK is used to reduce the data dimension. Three different schemes are proposed: (a) Parallel Dimension Reduction Scheme (PDRS): features in the form of Gabor wavelets are extracted from each sample image as shown in Figure 10. Each MGC projection matrix for each channel is trained, and the union These features are performed by voting. (b) Ensemble Dimension Reduction Scheme, EDRS): SURA is the most common scheme used for Gabor features. As shown in Figure 11, the difference between SPUR and SURA is that SURA combines Gabor's features instead of using them in parallel. (c) Multi-channel Dimension Reduction , MDRS. Xiaodong Li et al. [21] proposed the SMMS in 2009. As shown in Figure 12, the main idea of the SMMS is to train the MHC projection matrix for one channel using different sample images. In [21], Xiaodong Li et al. Already proved that SMUR works better than SURA using Gabor's features.
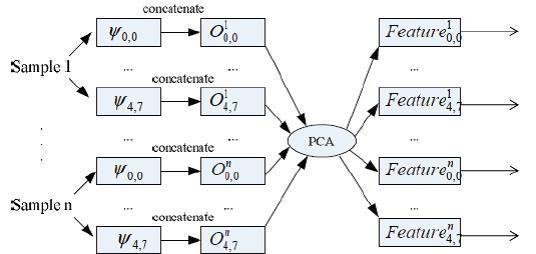
Figure 10. Scheme of parallel dimension reduction
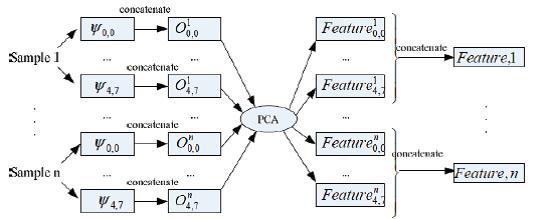
Figure 11. Scheme of ensemble dimension reduction
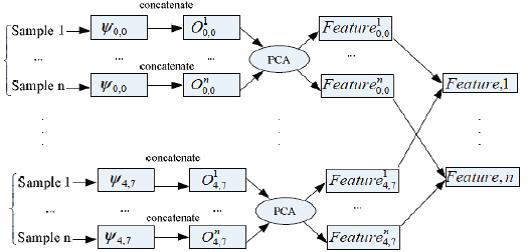
Figure 12. Scheme of multichannel dimension reduction
To compare the operation of SPUR and SMUR, the method of k-nearest neighbors (KNN) is used. For SPUR, we use a voting method called “Gaussian voting” to combine 40 channels. The concept of Gaussian voting is described as using a KNN classifier for each channel to predict 40 ages. Each predicted age is considered as the mathematical expectation of a normal distribution and defines a histogram. Its highest peak is the final predicted age value. For SMUR we use the combined features directly. The FG-NET age database [22] is adapted for experiments. The database contains 1002 images of people's faces (color and grayscale) with a large variation in lighting, postures and expressions of emotions. This database contains 82 different people (of different races) with ages from 0 to 69 years.mean absolute error , MAE) to evaluate the performance of each age estimation method. CAO means the average value of the absolute error between the estimated and known ages. The mathematical function of the CAO has the form:

where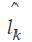 is the known age for the test image k, and
is the known age for the test image k, and  is the estimated age. N is the total number of tested images. Table 1 shows the experimental results for the two schemes. SMUR turned out to be better than SPUR.
is the estimated age. N is the total number of tested images. Table 1 shows the experimental results for the two schemes. SMUR turned out to be better than SPUR.
Table 1. Values of the CAO for SPUR and SMUR

3.3 Selection of features
The dimension of the Gabor wavelet space is extremely large, even despite the use of a dimensional reduction scheme. Therefore, it is important to choose the most significant features and further reduce the dimension of space. Three typical dimensional reduction methods have been proposed in recent studies: (a) linear discriminant analysis(LDA) is similar to MGK, but with the difference that LDA uses class information to improve itself [23]. (b) Preservation of local projections (LPP) is looking for a subspace that preserves the necessary diversity by measuring the distance to neighboring points [24]. OLPP produces orthogonal basis functions based on LPP and preserves the metric structure [25]. To determine which reduction method from the above is most suitable for using age-related features in the form of Gabor wavelets, we used the KNN classifier and the CAO criterion to evaluate the effectiveness. In the experiment, we changed the proximity weight of LPP and OLPP to get more detail. Table 2 shows the CAO values for each reduction method. Cosine distance weighted OLPP is most effective in estimating age.
Table 2. CAO for different methods of reducing the dimension

3.4 Age classification
Features in the form of Gabor wavelets are used in the MOB-classifier to determine the age. MOB has sufficient potential as a classifier of discharged training data. MOV has roots similar to neural networks and, like them, has the ability to approximate any function of many variables with any desired accuracy. This approach was invented by Vladimir Vapnik et al. Using statistical theory. [25-27]. Table 1 and Figure 11 show the results of comparing our conditionally based on the entropy approach to the selection of features with these approaches to the selection of features and classification. All comparisons in this article use the same training and test database. The database contains 1002 images of people's faces (color and grayscale) with a large variation in lighting, postures and expressions of emotions. This database contains 82 different people (of different races) with ages from 0 to 69 years. We used the input dimension of the MOV equal to 43 in the comparison process (as shown in table 2). In addition, we compared the accuracy with the same Gabor features and the KNN method.
4. Experimental results
We used an adapted FG-NET database of images of people of different ages [20]. This database is publicly available and contains 1002 images of people's faces (color and grayscale) with a large variation in lighting, postures and expressions of emotions. This database contains 82 different people (of different races) with ages from 0 to 69 years. Figure 13 shows a series of base images for one of the persons.

Figure 13. Some images of the person in the FG-NET database
To evaluate the operation of the age estimation subsystem, the face area on the images was identified using the face detector described in section 2. The method of cross-checking, in which at each step of the verification, only one person was used as a test, and the rest were used for training. Moreover, all persons of the sample were used alternately as a test person.
Each image was cropped and reduced to a size of 64 * 64 pixels, and color information was converted to 256 gray levels. We used a MOS with a RBF ( Radial basis function kernel , RBF) core, in which the parameter c = 0.5 and the gamma g = 0.0078125. We mainly focused on new features derived from Gabor wavelets.
The work of the age assessment subsystem can be evaluated using two measures: the average absolute error (CAO) and the cumulative sum (NS). CAO is defined as the average absolute error between the estimated age and the known. CAO was used in [2-10]. NS is defined as follows:

where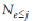 is the number of tested images on which the age estimate has an absolute error of no more than j.
is the number of tested images on which the age estimate has an absolute error of no more than j.
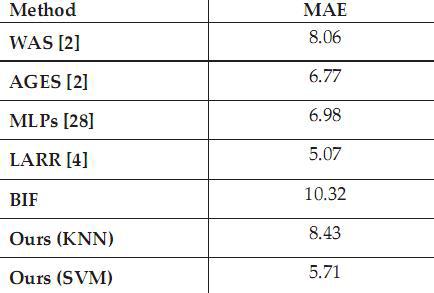
Table 3 shows the results of the experiment. We compare our results with previous methods using the FG-NET age database. The Gabor-OLSS method used in this work has a CAO equal to 8.43 and 5.71 when using KNN and MOB, respectively, which are clearly less than most previous results from similar experiments. Our method offers approximately 16% of SAO in comparison with the results of AGES [2]. In table 3, it can be seen that the LARR [4] method and the BIF [9] method have more favorable CAO values: 5.07 and 4.77 than ours.
Table 3. Values of CAO for different methods
As mentioned earlier, our goal is to build a fully automatic age rating system. The LARR method uses the AAM features of FG-NET directly and this means that this method usually needs to involve people in aligning characteristic points. Our study does not yet have an effective method that could automatically align points quickly and correctly. For example, the LARR method may require considerable effort in aligning points. CAO in BIF is clearly more effective than the method proposed by us. To verify their results, we tried to implement the BIF method. The results were much worse with CAO 10.32. Moreover, the BIF method takes a lot of time to extract aging features. Compared to our method, BIF requires twice as much time.
NS comparisons are illustrated in Figure 14. Our Gabor-OLPP method is faster than WAS and multilayer perceptron methods. The AGES method is similar to the GAbor-OLPP method at a low level of age error, but lower than those of Gabor-OLPP, where the error level is more than five.

Figure 14. Cumulative sum for each method
5. Conclusion
In this work, we proposed a new system for automatic age estimation by facial image. The Gabor wavelet-based transformation is introduced primarily for estimating age in order to extract age-related features automatically in real time. The support vector method has good potential for classifying discharged training data, and also has a stable ability to generalize.
In the most recent studies in this area, the principal component analysis method is used only to reduce the dimensionality of Gabor's features. But MGK has inadequate efficiency when Gabor's features are used directly. By increasing efficiency by reducing classification accuracy, previous researchers tried to select certain features, ignoring all the others. Therefore, dimensional reduction methods are more convenient for selecting target features. We compared four different typical methods for reducing data dimension. OLPP provides the vector of features of the smallest dimension and the most convenient selection of features.
6. Acknowledgments
This work was supported by the Department of Industrial Technology under the grant: 100 ‐ EC-17 ‐ A ‐ 02 ‐ S1‐032, and also, in part, by the Council of Taiwanese National Science under the grant: NSC ‐ 100‐2218-E ‐ 009‐023.
References
[1] Paul V, Jones MJ (2004) Robust Real ‐ Time Face Detection. International Journal of Computer Vision 57 (2), 137-154
[2] Geng X, Zhou Z ‐ H, Zhang Y, Li G, Dai H. (2006) Learning from facial aging patterns for automatic age estimation, In ACM Conf. on Multimedia, pages 307–316
[3] Geng X, Zhou Z ‐ H, Smith ‐ Miles K. (2007) Automatic age estimation based on facial aging patterns. IEEE Trans. on PAMI, 29 (12): 2234–2240
[4] Guo G, Fu Y, Dyer, CR, Huang, TS (2008) Image ‐ Based Human Age Estimation by Manifold Learning and Locally Adjusted Robust Regression. IEEE Trans. on Image Processing, 17 (7): 1178-1188
[5] Guo G, Fu Y, Huang TS and Dyer, CR (2008) Locally Adjusted Robust Regression for Human Age Estimation. IEEE Workshop on Applications of Computer Vision, pages 1-6 ,.
[6] Kwon Y, Lobo N. (1999) Age classification from facial images. Computer Vision and Image Understanding, 74 (1): 1–21
[7] Txia J ‐ D and Huang C ‐ L. (2009) Age Estimation Using AAM and Local Facial Features. Fifth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, pages 885-888
[8] Yan S ‐ C, Zhou X and Liu M. Hasegawa ‐ Johnson, M., Huang, TS (2008) Regression from patch ‐ kernel. IEEE Conference on CVPR, pages 1-8
[9] Guo G, Mu G, Fu Y and Huang TS (2009) Human age assessment using bio-inspired features. IEEE Conference on CVPR, pages 112-119.
[10] Serre T, Wolf L, Bileschi S, Riesenhuber M and Poggio T. (2007) “Robust Object Recognition with Cortex ‐ Like Mechanisms. IEEE Trans. on PAMI, 29 (3): 411–426
[11] Lin C ‐ T, Siana L, Shou Y ‐ W, Yang C ‐ T (2010) Multiclient Identification System using the Adaptive
Probabilistic Model. EURASIP Journal on Advances in Signal Processing. Vol. 2010
[12] Paul V and Jones MJ (2004) Robust Real ‐ Time Face Detection. International Journal of Computer Vision 57 (2), 137-154
[13] Papageorgiou C. P, Oren M and Poggio T. (1998) A general framework for object detection. in
Proceedings of the 6th IEEE International Conference on Computer Vision, pp. 555–562
[14] Viola P and Jones MJ (2004) Robust real ‐ time face detection. International Journal of Computer Vision, vol. 57, no. 2, pp. 137–154
[15] Donato G, Bartlett MS, Hager JC, Ekman P and Sejnowski TJ (1999) Classifying facial actions. IEEE Trans. Pattern Anal. Machine Intell., Vol. 21, pp. 974–989
[16] Wiskott L, Fellous J, Kruger N and Malsburg C. (1997) Face recognition by elastic bunch graph matching. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, pp. 775–779
[17] Liu C and Wechsler H. (2002) Gabor feature based classification using enhanced fisher linear discriminant model for face recognition. IEEE Transactions on Image Processing, vol. 11, pp. 467–476
[18] Liu C. (2004) Gabor ‐ based kernel PCA with fractional power polynomial models for face recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, pp. 572-581.
[19] Belhumeur PN, Hespanha JP and Kriegman DJ (1997). ʺEigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence 19 (7): 711‐ 720.
[20] Duda RO, Hart PE, and Stork DG (2000) Pattern Classification, 2nd ed. New York: Wiley Interscience
[21] Li X, Fei S and Zhang T. (2009) Novel Dimension Reduction Method of Gabor Feature and Its Application to Face Recognition. International Congress on Image and Signal Processing, 2009. CISP ʹ09. 2nd, Page (s): 1-5
[22] The FG ‐ NET Aging Database [Online]. Available: www.fgnet.rsunit.com
[23] He X ‐ F, Yan S ‐ C, Hu Y ‐ X, Niyogi P and Zhang H ‐ J. (2005) Face recognition using Laplacianfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (3): 328-340.
[24] Cai D, He X ‐ F, Han J ‐ W and Zhang H ‐ J. (2006) Orthogonal Laplacianfaces for Face Recognition. IEEE Transactions on Image Processing 15 (11): 3608‐3614.
[25] Mercier G and Lennon M. (2003) Support vector machines for hyperspectral image classification with spectral ‐ based kernels. in Proc. IGARSS, Toulouse, France, July 21–25.
[26] Abe S. (2005) Support Vector Machines for Pattern Classification. London: Springer ‐ Verlag London Limited.
[27] Wang L. (2005) Support Vector Machines: Theory and Applications. New York: Springer, Berlin.
[28] Lanitis A, Draganova C and Christodoulou C. (2004) Comparing different classifiers for automatic age estimation. IEEE Trans. Syst., Man, Cybern. B, Cybern., Vol. 34, no. 1, pp. 621–628
People are the most important tracking objects in video surveillance systems. However, tracking a person alone does not provide sufficient information about his motives, intentions, desires, etc. In this work, we present a new and reliable system for automatic age estimation using computer vision technology. It uses global facial features obtained by combining Gabor wavelets and preserving the orthogonality of local projections Orthogonal Locality Preserving Projections, OLPP). In addition, the system is capable of estimating age from real-time images. This means that the proposed system has greater potential compared to other semi-automatic systems. The results obtained in the application of the proposed approach can provide a clearer understanding of the algorithms in the field of age estimation necessary for developing applications relevant for real applications.
Keywords: Gabor wavelets, face image, age estimation, support vector machine ( Support Vector Machine , SVM).
1. Introduction
The image of a human face contains abundant information about a person, including facial features, emotions, gender, age, etc. In general, an image of a person’s face can be considered as a complex signal, consisting of many face properties, such as: skin color, geometric features of facial features . These attributes play an important role in real face image analysis applications. In such applications, various properties (attributes) evaluated from the captured face image can be used for further reaction (actions) of the system. Age, in particular, is one of the most important attributes. For example, users may require an age-dependent interactive computer system, or a system that can estimate age to provide access control, or a system for collecting intelligence.
The automatic age estimation system consists of two parts: face detection in the image and the age estimate itself. It is quite difficult to detect faces in the image, because the detection results are highly dependent on many conditions: environment, movement, lighting, orientation of faces in space, expression of emotions. These factors can lead to distortions in the color, brightness, shadows, and contours of images. For this reason, Viola and Jones proposed their famous face detection system in 2004. The Viola-Jones classifier uses the AdaBoost algorithm at each node of the classifier cascade to train a high degree of face detection by reducing the number of faces ignored throughout the cascade. This algorithm has the following features: 1) uses Haar features- comparison of differences in the sums of intensities of pixels in two rectangular areas with threshold values; 2) the use of an integrated image to accelerate the calculation of the sums of pixels in a rectangular region or a rectangular region rotated by an angle of 45 degrees; 3) the AdaBoost algorithm uses statistical boosting to create binary (face - not face) classification nodes characterized by a good probability of detecting faces and a low probability of missing a face; 4) nodes of weak classifiers are organized in a cascade with the aim of eliminating non-face images at the initial stage of the algorithm (i.e., the first levels of the cascade allow more errors of incorrect classification, but work faster than the subsequent levels of the cascade classifier). A person is classified as a person
Although automatic detection of faces in an image is a mature technique involving many applications, estimating age from a face image is still a difficult task. This is because the aging process is expressed differently, not only among different races, but also within the race. This process is mostly personal. In addition, it is also determined by the influence of external factors: lifestyle (proper nutrition, sport), place of residence, weather conditions. Therefore, the issue of sustainable age estimates is an open problem.
In general, there are three categories of feature extraction methods for assessing a person’s age in the literature. The first category is statistical approaches. Xin Geng et al. [2, 3] proposed AGing pattErn Subspace (AGES), a method for automatic age estimation. The idea of this approach is to model the pattern (pattern) of aging, which is determined by the sequence of personal images of facial aging. This model is built by studying subspace like an EM iterative learning method for principal components analysis (PCA). In other works [4, 5], Guodong Guo et al. Compare three typical methods for reducing dimensions of feature spaces and various embedding methods such as: PCA, locally linear embedding (Locally Linear Embedding (LLE), Orthogonal Locality Preserving Projections (OLPP). According to the distribution of data in the OLPP subspace, they offer the Locally Adjusted Robust Regression (LARR) method for training and predicting a person’s age. LARR uses Support Vector Regression (SVR) for rough prediction and determines local settings within a small limited range of ages centered on the result using the Support Vector Machine (SVM) method .
The second category of methods includes an approach based on the Active Appearance Model (AAM). Using the appearance model is the most intuitive method among all face image analysis methods.
Young H. Kwon et al. [6] used visual age features to construct an anthropometric model. Primary features are the eyes, nose, mouth and chin. The relations of these features were calculated to distinguish between different age categories. When analyzing secondary features, a wrinkle map was used to control the detection and measurement of wrinkles. Jun ‐ Da Txia et al. [7] proposed an age estimation method based on the active appearance model(AAM) for extracting regions of age-specific features. Each face requires the calculation of 28 special points and is divided into 10 regions of wrinkles. Shuicheng Yan et al. [8] used a path-based appearance model called Patch-Kernel. This method is designed to determine the Kullback-Leibler distance between models that are derived from the global model of Gaussian mixtures (GMM) using the maximum a Posteriori probability ( MAP) of any two images. The ability to classify was then enhanced by the use of a weak learning process called intermodal similarity synchronization. Nuclear regression is used at the end to estimate age.
The third category of methods uses a frequency-based approach. In image processing and pattern recognition, frequency domain analysis is one of the most popular methods for extracting image features. Guodong Guo et al. [9] investigated the "biological" image features ( biologically inspired features , BIF) to estimate the age of people image. Unlike previous works [4, 5], Guo modeled a person’s face using Gabor filters [10]. Gabor filters are linear filters used in image processing to highlight the boundaries of objects within an image. The frequency and orientation of the Gabor filter representations is similar to human vision and is well suited for texture representation and solving the discrimination problem.
Our system uses cascaded AdaBoost for training for face detection, and receives an estimate of age through the use of Gabor and OLPP wavelets. This article consists of the following sections. The first includes a description of the face detection system: histogram alignment, feature selection, cascading classifier, trained AdaBoost and the algorithm for clustering regions of the face image. The second section: the process of assessing age includes extracting features using Gabor wavelets, sifting out features and choosing the best, classifying the age. At the end of the article, the simulation results and conclusions are drawn.
This article proposes a fully automatic age rating system that uses Gabor wavelets to represent the aging process. The system we offer has 4 main modules: 1) face detection; 2) analysis based on Gabor wavelets; 3) OLPP reduction; 4) classification by the method of support vectors. The input image can come from the camera or read from a file. The face image is selected from the original image using the face detector using the approach described in [12]. Then the image is scaled to have a size of 64 * 64 pixels. Then, using 40 Gabor wavelet cores, features are extracted and OLPP reduction is applied to them. In the end, an age assessment is started using the trained SVM classifier.
The rest of the article is organized as follows: Section 2 describes the face detection subsystem using AdaBoost. Section 3 describes the age estimation algorithm and includes: texture analysis by Gabor wavelets, OLPP reduction, and SVM classification. Section 4 presents experimental results. Section 5 draws conclusions on the proposed system.

Figure 1. System Overview
2. Face Detection
Figure 1 shows the architecture of the automatic age estimation system proposed in our work. The whole system consists of a face detection subsystem, the task of which is to detect areas of faces in the image and age estimation subsystems. To search for faces in the image, scanning windows of various sizes are used, because when capturing an image, the object may be at different distances from the camera. There are a total of 12 scale levels of scanning, and the image size changes starting from 24 * 24 with a scale factor of 1.25. Depending on the lighting conditions in which the image is captured, there may be various variations in the brightness of the images. The image can be more accurately recognized (more precisely, the face in the image) after normalizing its brightness.
2.1. Normalization of illumination
Normalization of illumination is based on the method of alignment (adjustment) of histograms. The primary task of fitting the histograms is to convert the original histogram H (l) to the target histogram G (l). The target histogram G (l) is selected as the image histogram close to the average histogram for the face database. Select the target image and the histogram G (l) as shown in Figure 2 (a). Images before and after normalization are shown in Figures 2 (b) -.

Figure 2. Normalization of illumination. (a) Target image. (b) Input images. (c) Normalized images
Input images that are too dark or too light are normalized according to the histogram of the target image. The histograms H (l) are converted to the histograms G (l) as follows:
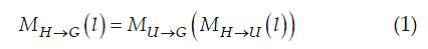
where
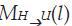 and
and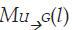 - direct and inverse mapping of histograms H (l) and G (l) into histograms of homogeneous (uniform) distributions.
- direct and inverse mapping of histograms H (l) and G (l) into histograms of homogeneous (uniform) distributions. 2.2 Selection of features
We have selected four rectangular Haar features as shown in Figure 3 [13].

Figure 3. Four types of rectangular features
It is permissible to use a composition of rectangles of different brightness to represent light and dark regions of the image. Features are defined as follows:
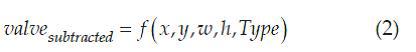
where (x, y) denotes the center of the relative coordinate system of the rectangular feature in the scanning window. The importance of w and h denotes the relative width and height of the rectangular feature, respectively. Type - type of rectangular feature,
 - the difference of the sums of pixels in the light and dark areas.
- the difference of the sums of pixels in the light and dark areas.A rectangular feature that can effectively separate faces from non-faces is considered a weak classifier:

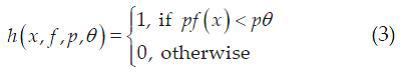
A weak classifier is
 used to determine if the current part of the image is a face or not a face based on counting a rectangular feature, threshold q, and polarity (direction of inequality) p. For each weak classifier, the optimal threshold is chosen so as to minimize the error of incorrect classification. The threshold is selected by training on a sample of 4000 face images and 59000 non-face images. Figures 4 (a) - (b) are examples from databases of individuals and non-individuals. In this procedure, we calculate the distribution of each feature
used to determine if the current part of the image is a face or not a face based on counting a rectangular feature, threshold q, and polarity (direction of inequality) p. For each weak classifier, the optimal threshold is chosen so as to minimize the error of incorrect classification. The threshold is selected by training on a sample of 4000 face images and 59000 non-face images. Figures 4 (a) - (b) are examples from databases of individuals and non-individuals. In this procedure, we calculate the distribution of each feature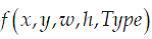 for each image in the database, and select a threshold that has the maximum discriminative ability (i.e. breaks the image into two classes better than the rest).
for each image in the database, and select a threshold that has the maximum discriminative ability (i.e. breaks the image into two classes better than the rest). 
Figure 4. Database of faces (a) and non-faces (b)
Although each rectangular feature is calculated very efficiently, calculating all combinations is very computationally expensive. For example, for the smallest sliding window (24 * 24), the full set of features is 160,000.
The AdaBoost algorithm combines a set of weak classifiers to form a strong classifier. Although a strong classifier is effective for face detection applications, it has been running for quite some time. The cascading classifier structure, which improves detection ability and reduces computation time, was proposed by Viola and Jones [14]. Based on this idea, our cascading AdaBoost forms a strong classifier. In the first step, if the image from the sliding window is classified as a face, then we go to step 2, in another case, the image is discarded. A similar process is performed for all steps. The number of steps should be sufficient to achieve a good degree of recognition and at the same time, should minimize the computation time. For example, if at each step the probability of detecting a face is 0.99, The 10-step classifier will reach a probability of 0.9 (since 0.9 ~ = 0.99 ^ 10). Although achieving this probability may sound like a very difficult task, it can be done easily, since each step should have a false positive recognition error value of only about 30%.
The operation procedure of the AdaBoost algorithm can be described as follows: if m and l are the numbers of persons and non-persons, respectively, and j is the sum of non-persons and persons. The initial weights w_ (i, j) for the ith step can be defined as
 . The normalized weighted error of a weak classifier can be expressed as follows:
. The normalized weighted error of a weak classifier can be expressed as follows: 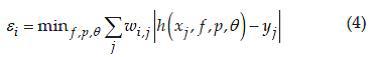
Weights are updated according to formula (5) in each iteration. If the object is classified correctly, then
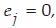 in the remaining cases ej = 1.
in the remaining cases ej = 1. 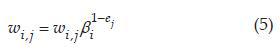
The final classifier for the i-th step is defined below:

where
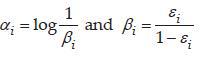
2.3 Area-based clustering
A face detector usually finds more than one face, even if it has one face (as shown in Figure 5).

Figure 5. The results of the face detector
Therefore, area-based clustering is used to solve this problem. The proposed method consists of two levels of clustering - local and global clustering. Local clustering is used to cluster blocks on a single scale and form a simple filter to determine the number of image blocks within clusters. If the number of blocks in a cluster is more than one, then this cluster is marked as probably containing a person, otherwise, the cluster is rejected. The local clustering method also has the following rule for deciding on cluster
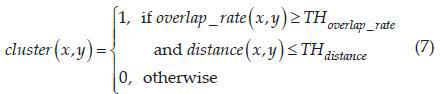
labeling : In formula (7), the percentage of overlap (x, y) denotes the distance between two detected candidate regions and is equal to the distance between the centers of these regions. Equality
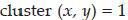 means that x and y are in the same cluster and these regions almost completely overlap each other
means that x and y are in the same cluster and these regions almost completely overlap each other Figure 6 shows several possible cases of overlapping regions.

Figure 6. Diagrams of overlapping regions and distance of block centers
In Figure 6 (a), two blocks fall into one cluster. In Figure 6 (b), two blocks fall into different clusters, because the distance between their centers is greater than the threshold. For special cases, as shown in Figure 6 (c), all blocks are considered as candidates, but most of them are false faces. Therefore, in this work, for practical applications, we select only one block that satisfies equation (7) rather than several blocks. In the end, global clustering will use the blocks obtained during the local clustering stage, and the label of the facial region corresponds to the average size of all available blocks. Some results of the entire clustering process based on the choice of regions for the local and global levels are shown in Figure 7. From the right image in Figure 7, in fact,

Figure 7. Clustering results. (a) Local clustering results. (b) Global Clustering Results
3. Age Estimation
There are three main parts of our age rating system presented in this work: extracting age features, reducing the number of features, and classifying features. Feature extraction is performed using Gabor wavelets, which are used to analyze images because of their biological significance and computational properties. Gabor wavelet kernels are similar to the 2D perception of milk bacteria and expressing powerful spatial orientation and selectivity abilities, as well as being locally optimal in the spatial and frequency domains. Gabor transformation is well known, especially suitable for decomposition of images and their presentation, when the goal is the choice of local and distinctive features. Moreover, Donato and others [15] showed experimentally, that the representation through Gabor wavelets is effective for classifying facial features. This section introduces the basics of Gabor wavelets to represent the features of images and describes the reduction in the number of features, their selection into a vector used to estimate age.
3.1 Extraction of features using wavelets Gabor
Wavelet Gabor
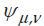 can be defined as follows [16]:
can be defined as follows [16]: 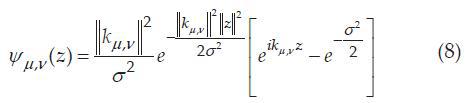
where
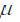 and
and 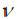 determine the orientation and scale Gabor kernel
determine the orientation and scale Gabor kernel  denotes an operator of calculating the norm, and the wave vector
denotes an operator of calculating the norm, and the wave vector  is defined as follows:
is defined as follows: 
where
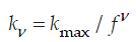 and
and  - the maximum frequency, and f - spatial factor between cores in the frequency domain. In general, the Gabor wavelet kernels in (8) are self-similar, since they can be derived from one filter, the mother wavelet, by scaling and rotation using the wave vector
- the maximum frequency, and f - spatial factor between cores in the frequency domain. In general, the Gabor wavelet kernels in (8) are self-similar, since they can be derived from one filter, the mother wavelet, by scaling and rotation using the wave vector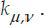 Each core is a product of a Gaussian convolution and a complex wave plane, while the first term in square brackets in (9) defines the vibrational part of the core, and the second term compensates for the direct current value. The sigma parameter is the standard deviation of the width of the Gaussian convolution from the wavelength.
Each core is a product of a Gaussian convolution and a complex wave plane, while the first term in square brackets in (9) defines the vibrational part of the core, and the second term compensates for the direct current value. The sigma parameter is the standard deviation of the width of the Gaussian convolution from the wavelength. In most cases, researchers use Gabor wavelets with five different scales,
 and eight orientations.
and eight orientations.  Figure 8 shows the real part of Gabor cores at 5 scale levels and 8 directions, as well as their values for the following parameters:
Figure 8 shows the real part of Gabor cores at 5 scale levels and 8 directions, as well as their values for the following parameters: 
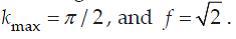

Figure 8. Representation of Gabor
wavelets Representation of wavelets Gabor for an image is a convolution of an image with a family of Gabor kernels using equation (8). Let be
 - distribution of gray image levels. The result of the convolution of image I
- distribution of gray image levels. The result of the convolution of image I 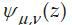 is defined as:
is defined as: 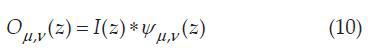
where
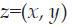 and * denotes the operator of convolution (convolution).
and * denotes the operator of convolution (convolution). Using the convolution theorem, the fast Fourier transform (FFT) is used to obtain the result of the convolution operation. Equations (11) and (12) are the definition of convolution through FFT.
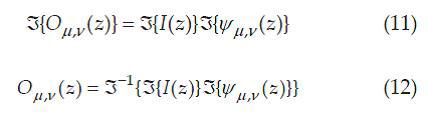
where
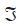 and
and 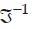 denote the Fourier transform and the inverse Fourier transform, respectively.
denote the Fourier transform and the inverse Fourier transform, respectively. 
Figure 9. One of the sampled images and 40 outputs of the convolution operation
Figure 9 shows the output values of the convolution operations for the sample image. In accordance with Figure 9, the output convolution values exhibit spatial orientation and selectivity. Such characteristics produce robust local features that are suitable for visual recognition. Further, we denote the
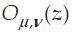 value of the outputs of the convolution operation.
value of the outputs of the convolution operation. 3.2 Reducing the number of features according to the scheme
In general, MGCs or other algorithms work with features in the form of Gabor wavelets to reduce the dimension of the converted data [19, 20]. Convolution results, corresponding to all Gabor wavelets, are brought together as a whole, and in order to improve computational efficiency, MGK is used to reduce the data dimension. Three different schemes are proposed: (a) Parallel Dimension Reduction Scheme (PDRS): features in the form of Gabor wavelets are extracted from each sample image as shown in Figure 10. Each MGC projection matrix for each channel is trained, and the union These features are performed by voting. (b) Ensemble Dimension Reduction Scheme, EDRS): SURA is the most common scheme used for Gabor features. As shown in Figure 11, the difference between SPUR and SURA is that SURA combines Gabor's features instead of using them in parallel. (c) Multi-channel Dimension Reduction , MDRS. Xiaodong Li et al. [21] proposed the SMMS in 2009. As shown in Figure 12, the main idea of the SMMS is to train the MHC projection matrix for one channel using different sample images. In [21], Xiaodong Li et al. Already proved that SMUR works better than SURA using Gabor's features.

Figure 10. Scheme of parallel dimension reduction

Figure 11. Scheme of ensemble dimension reduction

Figure 12. Scheme of multichannel dimension reduction
To compare the operation of SPUR and SMUR, the method of k-nearest neighbors (KNN) is used. For SPUR, we use a voting method called “Gaussian voting” to combine 40 channels. The concept of Gaussian voting is described as using a KNN classifier for each channel to predict 40 ages. Each predicted age is considered as the mathematical expectation of a normal distribution and defines a histogram. Its highest peak is the final predicted age value. For SMUR we use the combined features directly. The FG-NET age database [22] is adapted for experiments. The database contains 1002 images of people's faces (color and grayscale) with a large variation in lighting, postures and expressions of emotions. This database contains 82 different people (of different races) with ages from 0 to 69 years.mean absolute error , MAE) to evaluate the performance of each age estimation method. CAO means the average value of the absolute error between the estimated and known ages. The mathematical function of the CAO has the form:

where
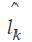 is the known age for the test image k, and
is the known age for the test image k, and  is the estimated age. N is the total number of tested images. Table 1 shows the experimental results for the two schemes. SMUR turned out to be better than SPUR.
is the estimated age. N is the total number of tested images. Table 1 shows the experimental results for the two schemes. SMUR turned out to be better than SPUR. Table 1. Values of the CAO for SPUR and SMUR

3.3 Selection of features
The dimension of the Gabor wavelet space is extremely large, even despite the use of a dimensional reduction scheme. Therefore, it is important to choose the most significant features and further reduce the dimension of space. Three typical dimensional reduction methods have been proposed in recent studies: (a) linear discriminant analysis(LDA) is similar to MGK, but with the difference that LDA uses class information to improve itself [23]. (b) Preservation of local projections (LPP) is looking for a subspace that preserves the necessary diversity by measuring the distance to neighboring points [24]. OLPP produces orthogonal basis functions based on LPP and preserves the metric structure [25]. To determine which reduction method from the above is most suitable for using age-related features in the form of Gabor wavelets, we used the KNN classifier and the CAO criterion to evaluate the effectiveness. In the experiment, we changed the proximity weight of LPP and OLPP to get more detail. Table 2 shows the CAO values for each reduction method. Cosine distance weighted OLPP is most effective in estimating age.
Table 2. CAO for different methods of reducing the dimension

3.4 Age classification
Features in the form of Gabor wavelets are used in the MOB-classifier to determine the age. MOB has sufficient potential as a classifier of discharged training data. MOV has roots similar to neural networks and, like them, has the ability to approximate any function of many variables with any desired accuracy. This approach was invented by Vladimir Vapnik et al. Using statistical theory. [25-27]. Table 1 and Figure 11 show the results of comparing our conditionally based on the entropy approach to the selection of features with these approaches to the selection of features and classification. All comparisons in this article use the same training and test database. The database contains 1002 images of people's faces (color and grayscale) with a large variation in lighting, postures and expressions of emotions. This database contains 82 different people (of different races) with ages from 0 to 69 years. We used the input dimension of the MOV equal to 43 in the comparison process (as shown in table 2). In addition, we compared the accuracy with the same Gabor features and the KNN method.
4. Experimental results
We used an adapted FG-NET database of images of people of different ages [20]. This database is publicly available and contains 1002 images of people's faces (color and grayscale) with a large variation in lighting, postures and expressions of emotions. This database contains 82 different people (of different races) with ages from 0 to 69 years. Figure 13 shows a series of base images for one of the persons.

Figure 13. Some images of the person in the FG-NET database
To evaluate the operation of the age estimation subsystem, the face area on the images was identified using the face detector described in section 2. The method of cross-checking, in which at each step of the verification, only one person was used as a test, and the rest were used for training. Moreover, all persons of the sample were used alternately as a test person.
Each image was cropped and reduced to a size of 64 * 64 pixels, and color information was converted to 256 gray levels. We used a MOS with a RBF ( Radial basis function kernel , RBF) core, in which the parameter c = 0.5 and the gamma g = 0.0078125. We mainly focused on new features derived from Gabor wavelets.
The work of the age assessment subsystem can be evaluated using two measures: the average absolute error (CAO) and the cumulative sum (NS). CAO is defined as the average absolute error between the estimated age and the known. CAO was used in [2-10]. NS is defined as follows:

where
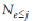 is the number of tested images on which the age estimate has an absolute error of no more than j.
is the number of tested images on which the age estimate has an absolute error of no more than j.Table 3 shows the results of the experiment. We compare our results with previous methods using the FG-NET age database. The Gabor-OLSS method used in this work has a CAO equal to 8.43 and 5.71 when using KNN and MOB, respectively, which are clearly less than most previous results from similar experiments. Our method offers approximately 16% of SAO in comparison with the results of AGES [2]. In table 3, it can be seen that the LARR [4] method and the BIF [9] method have more favorable CAO values: 5.07 and 4.77 than ours.
Table 3. Values of CAO for different methods

As mentioned earlier, our goal is to build a fully automatic age rating system. The LARR method uses the AAM features of FG-NET directly and this means that this method usually needs to involve people in aligning characteristic points. Our study does not yet have an effective method that could automatically align points quickly and correctly. For example, the LARR method may require considerable effort in aligning points. CAO in BIF is clearly more effective than the method proposed by us. To verify their results, we tried to implement the BIF method. The results were much worse with CAO 10.32. Moreover, the BIF method takes a lot of time to extract aging features. Compared to our method, BIF requires twice as much time.
NS comparisons are illustrated in Figure 14. Our Gabor-OLPP method is faster than WAS and multilayer perceptron methods. The AGES method is similar to the GAbor-OLPP method at a low level of age error, but lower than those of Gabor-OLPP, where the error level is more than five.

Figure 14. Cumulative sum for each method
5. Conclusion
In this work, we proposed a new system for automatic age estimation by facial image. The Gabor wavelet-based transformation is introduced primarily for estimating age in order to extract age-related features automatically in real time. The support vector method has good potential for classifying discharged training data, and also has a stable ability to generalize.
In the most recent studies in this area, the principal component analysis method is used only to reduce the dimensionality of Gabor's features. But MGK has inadequate efficiency when Gabor's features are used directly. By increasing efficiency by reducing classification accuracy, previous researchers tried to select certain features, ignoring all the others. Therefore, dimensional reduction methods are more convenient for selecting target features. We compared four different typical methods for reducing data dimension. OLPP provides the vector of features of the smallest dimension and the most convenient selection of features.
6. Acknowledgments
This work was supported by the Department of Industrial Technology under the grant: 100 ‐ EC-17 ‐ A ‐ 02 ‐ S1‐032, and also, in part, by the Council of Taiwanese National Science under the grant: NSC ‐ 100‐2218-E ‐ 009‐023.
References
[1] Paul V, Jones MJ (2004) Robust Real ‐ Time Face Detection. International Journal of Computer Vision 57 (2), 137-154
[2] Geng X, Zhou Z ‐ H, Zhang Y, Li G, Dai H. (2006) Learning from facial aging patterns for automatic age estimation, In ACM Conf. on Multimedia, pages 307–316
[3] Geng X, Zhou Z ‐ H, Smith ‐ Miles K. (2007) Automatic age estimation based on facial aging patterns. IEEE Trans. on PAMI, 29 (12): 2234–2240
[4] Guo G, Fu Y, Dyer, CR, Huang, TS (2008) Image ‐ Based Human Age Estimation by Manifold Learning and Locally Adjusted Robust Regression. IEEE Trans. on Image Processing, 17 (7): 1178-1188
[5] Guo G, Fu Y, Huang TS and Dyer, CR (2008) Locally Adjusted Robust Regression for Human Age Estimation. IEEE Workshop on Applications of Computer Vision, pages 1-6 ,.
[6] Kwon Y, Lobo N. (1999) Age classification from facial images. Computer Vision and Image Understanding, 74 (1): 1–21
[7] Txia J ‐ D and Huang C ‐ L. (2009) Age Estimation Using AAM and Local Facial Features. Fifth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, pages 885-888
[8] Yan S ‐ C, Zhou X and Liu M. Hasegawa ‐ Johnson, M., Huang, TS (2008) Regression from patch ‐ kernel. IEEE Conference on CVPR, pages 1-8
[9] Guo G, Mu G, Fu Y and Huang TS (2009) Human age assessment using bio-inspired features. IEEE Conference on CVPR, pages 112-119.
[10] Serre T, Wolf L, Bileschi S, Riesenhuber M and Poggio T. (2007) “Robust Object Recognition with Cortex ‐ Like Mechanisms. IEEE Trans. on PAMI, 29 (3): 411–426
[11] Lin C ‐ T, Siana L, Shou Y ‐ W, Yang C ‐ T (2010) Multiclient Identification System using the Adaptive
Probabilistic Model. EURASIP Journal on Advances in Signal Processing. Vol. 2010
[12] Paul V and Jones MJ (2004) Robust Real ‐ Time Face Detection. International Journal of Computer Vision 57 (2), 137-154
[13] Papageorgiou C. P, Oren M and Poggio T. (1998) A general framework for object detection. in
Proceedings of the 6th IEEE International Conference on Computer Vision, pp. 555–562
[14] Viola P and Jones MJ (2004) Robust real ‐ time face detection. International Journal of Computer Vision, vol. 57, no. 2, pp. 137–154
[15] Donato G, Bartlett MS, Hager JC, Ekman P and Sejnowski TJ (1999) Classifying facial actions. IEEE Trans. Pattern Anal. Machine Intell., Vol. 21, pp. 974–989
[16] Wiskott L, Fellous J, Kruger N and Malsburg C. (1997) Face recognition by elastic bunch graph matching. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, pp. 775–779
[17] Liu C and Wechsler H. (2002) Gabor feature based classification using enhanced fisher linear discriminant model for face recognition. IEEE Transactions on Image Processing, vol. 11, pp. 467–476
[18] Liu C. (2004) Gabor ‐ based kernel PCA with fractional power polynomial models for face recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, pp. 572-581.
[19] Belhumeur PN, Hespanha JP and Kriegman DJ (1997). ʺEigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence 19 (7): 711‐ 720.
[20] Duda RO, Hart PE, and Stork DG (2000) Pattern Classification, 2nd ed. New York: Wiley Interscience
[21] Li X, Fei S and Zhang T. (2009) Novel Dimension Reduction Method of Gabor Feature and Its Application to Face Recognition. International Congress on Image and Signal Processing, 2009. CISP ʹ09. 2nd, Page (s): 1-5
[22] The FG ‐ NET Aging Database [Online]. Available: www.fgnet.rsunit.com
[23] He X ‐ F, Yan S ‐ C, Hu Y ‐ X, Niyogi P and Zhang H ‐ J. (2005) Face recognition using Laplacianfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (3): 328-340.
[24] Cai D, He X ‐ F, Han J ‐ W and Zhang H ‐ J. (2006) Orthogonal Laplacianfaces for Face Recognition. IEEE Transactions on Image Processing 15 (11): 3608‐3614.
[25] Mercier G and Lennon M. (2003) Support vector machines for hyperspectral image classification with spectral ‐ based kernels. in Proc. IGARSS, Toulouse, France, July 21–25.
[26] Abe S. (2005) Support Vector Machines for Pattern Classification. London: Springer ‐ Verlag London Limited.
[27] Wang L. (2005) Support Vector Machines: Theory and Applications. New York: Springer, Berlin.
[28] Lanitis A, Draganova C and Christodoulou C. (2004) Comparing different classifiers for automatic age estimation. IEEE Trans. Syst., Man, Cybern. B, Cybern., Vol. 34, no. 1, pp. 621–628
