MIT course "Security of computer systems". Lecture 10: "Symbolic Execution", part 3
- Transfer
- Tutorial
Massachusetts Institute of Technology. Lecture course # 6.858. "Security of computer systems." Nikolai Zeldovich, James Mykens. year 2014
Computer Systems Security is a course on the development and implementation of secure computer systems. Lectures cover threat models, attacks that compromise security, and security methods based on the latest scientific work. Topics include operating system (OS) security, capabilities, information flow control, language security, network protocols, hardware protection and security in web applications.
Lecture 1: “Introduction: threat models” Part 1 / Part 2 / Part 3
Lecture 2: “Control of hacker attacks” Part 1 / Part 2 / Part 3
Lecture 3: “Buffer overflow: exploits and protection” Part 1 /Part 2 / Part 3
Lecture 4: “Privilege Separation” Part 1 / Part 2 / Part 3
Lecture 5: “Where Security System Errors Come From” Part 1 / Part 2
Lecture 6: “Capabilities” Part 1 / Part 2 / Part 3
Lecture 7: “Native Client Sandbox” Part 1 / Part 2 / Part 3
Lecture 8: “Network Security Model” Part 1 / Part 2 / Part 3
Lecture 9: “Web Application Security” Part 1 / Part 2/ Part 3
Lecture 10: “Symbolic Execution” Part 1 / Part 2 / Part 3
Now, following the branch down, we see the expression t = y. Since we are considering one path at a time, we don’t have to introduce a new variable for t. We can simply say that t = y means that t is no longer equal to 0. We
continue to move down and get to the point where we fall into another branch. What is the new assumption that we must make in order to follow further down this path? This is an assumption that t <y.
What is t? If you look up the right branch, we see that t = y. And in our table T = y and Y = y. From this it follows logically that our constraint looks like y <y, which cannot be.
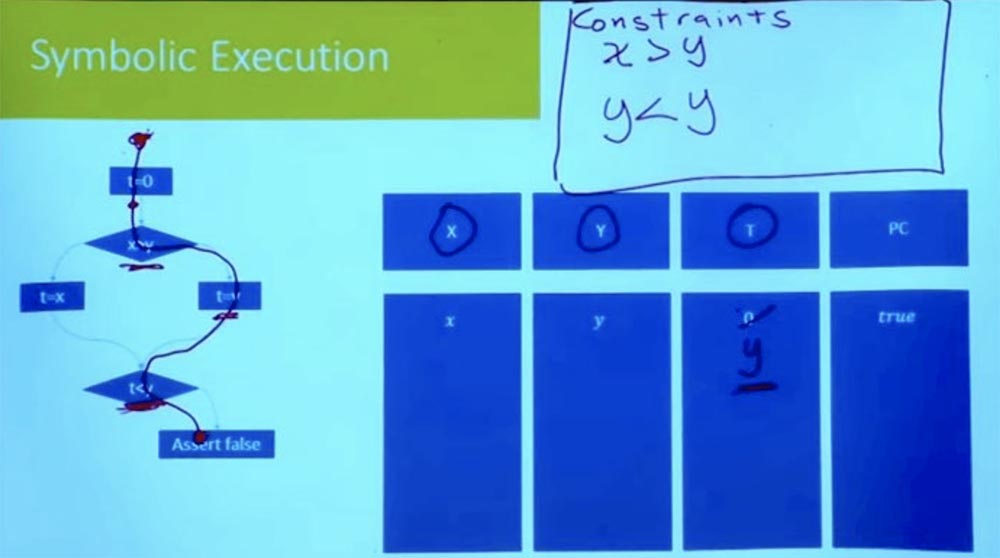
Thus, we had everything in order, until we reached this point t <y. Until we reach the statement of false, all inequalities must be correct. But this does not work, because when performing the tasks of the right branch, we get a logical discrepancy.
We have what is often called the condition of the path. This condition must be true for the program to go this way. But we know that this condition cannot be fulfilled, therefore it is impossible for the program to go this way. So this path is now completely eliminated, and we know that this right path cannot be traversed.
What about the other way? Let's try to pass the left branch in another way. What are the conditions for this path? Again, our character state begins with t = 0, and X and Y are equal to variables x and y.

What is the path constraint in this case now? Denote the left branch as True, and the right one as False, and then consider the value t = x. As a result of the logical processing of the conditions t = x, x> y and t <y, we get that we simultaneously have that x> y and x <y.
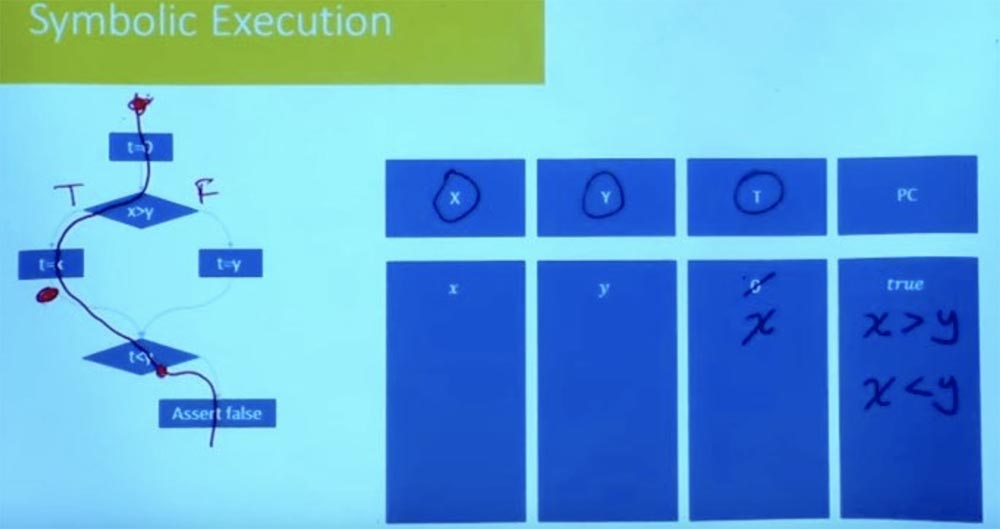
It is quite clear that this condition of the path is unsatisfactory. We cannot have x, which is both larger and smaller than y. There is no variable assignment X, which satisfies both constraints. So this tells us that the other way is also unsatisfactory.
It turns out that at this moment we explored all possible paths in the program that could lead us to this state. We can actually establish and certify that there is no possible way that would lead us to asserting false.
Audience: in this example, you showed that you studied the program in all possible branches. But one of the advantages of symbolic execution is that we do not need to study all possible exponential paths. So how to avoid this in this example?
Professor:This is a very good question. In this case, you reach a compromise between character execution and how specific you want to be. So in this case, we are not so much using symbolic execution as the first time, when we looked at the course of the program on both branches at the same time. But thanks to this, our limitations have become very, very simple.
Individual restrictions “one way after another” are very simple, but you have to do it again and again, studying all existing branches, and exponentially - all possible ways.
There are exponentially many paths, but for each path as a whole, there is also an exponentially large set of input data that can go along this path. So this already gives you a big advantage, because instead of trying all possible inputs, you are trying to try every possible way. But can you do something better?
This is one of the areas where many experiments have been made regarding symbolic execution, for example, the simultaneous execution of several paths. In the materials of the lecture, you met heuristics and a set of strategies that experimenters used to make the search more solvable.
For example, one of the things they do is that they explore one path after another, but they do not do it completely blindly. They check the conditions of the path after each step taken. Suppose that here in our program instead of the statement “false” there would be a complex program tree, a control flow graph.
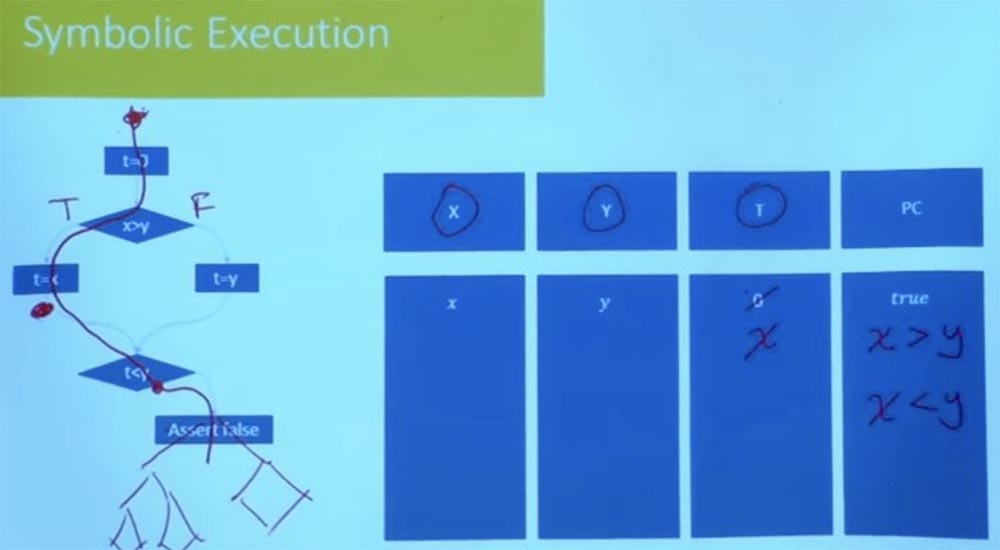
You do not need to wait until you reach the very end to check that this path is feasible. The moment you reach the condition t <y, you already know that this path is not satisfactory, and you will never go in that direction. Therefore, cutting off the wrong branches at the beginning of the program reduces the amount of empirical labor. Reasonable exploration of the path prevents the program from failing later. The set of practical tools that are used today, first of all, start with random testing to get an initial set of paths, after which they will begin to explore the paths in the neighborhood. They process a variety of options for the possible execution of a program for each of the branches, wondering what is happening on these paths.
Especially useful if we have a good test suite. You run your test and find out that this piece of code is not being executed. Therefore, you can take the path that was the closest to the implementation of the code, and ask if it is possible to change this path so that it goes in the right direction?

But the moment you try to do all the paths at the same time, constraints begin to become difficult to solve. Therefore, what you can do is perform one function at a time, and you can explore all the ways in a function together. If you try to make big blocks, then generally you can scout all possible paths.
The most important thing is that for each branch you check your limitations and set whether this branch can really go in both directions. If she cannot follow both ways, you save time and effort by not following in the direction where she cannot go. In addition, I do not remember the specific strategies that they use to find ways that are more likely to give a very good result. But cutting off the wrong branches at the initial stage is very important.
Until now, we have mostly talked only about “toy code”, about integer variables, about branches, about very simple things. But what happens when you have a more complex program? In particular, what happens when you have a program that includes a bunch?

Historically, a bunch of hip has been the curse of all software analysis, because the clean and elegant things of the times of Fortran explode completely when you try to run them with programs written in C, in which you allocate memory left and right. There you have overlays and all the mess that is associated with the work of the program with the allocated memory and with the arithmetic of pointers. This is one of the areas where symbolic execution has an outstanding ability to talk about programs.
So how do we do this? Let's forget about the branches and the flow of control for a minute. We have a simple program here. It allocates some memory, resets it, and receives a new pointer y from the pointer x. Then it writes something to y and checks whether the value stored in the pointer y is equal to the value stored in the pointer x?
Based on the basic knowledge of the C language, you can see that this check is not performed because x is zeroed and y = 25, so x indicates a different location. So far we are doing well.
The way in which we model the heap, and the way the heap is modeled in most systems, uses the heap representation in C, where it is simply a giant address base, a giant array in which you can arrange your data.
This means that we can represent our program as a very large global dataset, which will be called MEM. This is an array that, in essence, is going to map addresses to values. The address is just a 64-bit value. And what will happen after you read any of this address? It depends on how you model the memory.
If you model it at the level of bytes, it turns out to be a byte. If you model it at the word level, then the word is obtained. Depending on the type of errors you are interested in, and depending on whether you are concerned about memory allocation or not, you will model it a little differently, but usually memory is just an array from address to value.

So the address is just an integer. In a sense, it doesn't matter what C thinks about the address, it's just a whole 64-bit or 32-bit number, depending on your machine. This is just the value that is indexed in this memory. And what you can put in memory, then you can read from this memory.
Therefore, things like pointer arithmetic just become integer arithmetic. In practice, there are some difficulties, because in C, pointer arithmetic is aware of pointer types, and they will increase in proportion to size. So the result will be the following string:
y = x + 10; sizeof (int)

But what really matters is what happens when you write to memory and read from memory. Based on the pointer that you need to write 25 to y, I take an array of memory and index it with y. And I write 25 to this memory location.
Then I turn to the statement MEM [y] = = MEM [x], read the value from the y location in memory, read the value from the x location in memory and compare them to each other. So I check if they match.
This is a very simple assumption that allows you to move from a program that uses a heap to a program that uses this gigantic global array representing memory. This means that now, when reasoning about programs that manage the heap, you really do not need to reason about the programs that manage the heap. You'll be fine with the opportunity to talk about arrays, not heaps.
Here is another simple question. What about the malloc function? You can simply take and use the C implementation of malloc, keep track of all the selected pages, track everything that has been released, just have a free list, and that is enough. It turns out that for many purposes and for many types of errors you do not need malloc to be complex.
In fact, you can go from malloc, which looks like this: x = malloc (sizeof (int) * 100), to malloc of this type:
POS = 1
Int malloc (int n) {
rv = POS
POS + = n;
}
Which simply says: "I am going to save the counter for the next free memory space, and whenever someone asks for an address, I give him this location and increase this position, and then return rv." In this case, what is malloc in the traditional sense is completely ignored.

In this case, there is no release of memory. The function simply continues to move through the memory further, and further, and further, and that is all and ends without any release. She is also not very worried about the fact that there are areas of memory in which you should not write, because there are special addresses that have special meaning reserved for the operating system.
It does not model anything that makes writing the malloc function difficult, but only at a certain level of abstraction, when you try to reason about some complex code that manipulates the pointer.
In this case, you do not care about the release of memory, but it does care whether the program is going, for example, to write outside of some buffer, in which case the malloc function can be quite good.

And this actually happens very, very often when you do symbolic execution of a real code. A very important step is the modeling of the functions of your library. How you model library functions will have a huge impact, on the one hand, on the performance and scalability of the analysis, but on the other hand, will also affect accuracy.
So if you have such a “toy” malloc model, like this one, it will act very quickly, but there will be certain types of errors that you cannot notice. For example, in this model, I completely ignore the distribution, so I may get an error if someone gets access to unallocated space. Therefore, in real life, I will never use this mickey mouse malloc model.
So there is always a balance between analysis accuracy and efficiency. And the more complex the model of standard functions, such as malloc get, the less scalable their analysis. But for some classes of errors you will need these simple models. Therefore, various C libraries are of great importance, which are needed in order to understand what a program actually does.
Therefore, we have reduced the problem of reasoning about the heap, reasoning about a program with arrays, but I actually did not tell you how to reason about a program with arrays. It turns out that most SMT solvers support array theory.

The idea is that if a is an array, then there are some notation that allows you to take this array and create a new array, where location i is updated to the value e. It's clear?
Therefore, if I have an array a, and I do this update operation, and then I try to read the value of k, then this means that the value of k will be equal to the value of k in the array a, if k is different from i, and it will be equal to e, if k is i.
Updating an array means taking an old array and updating it with a new array. Well, if you have a formula that includes the theory of arrays, so I started with a zero array, which is represented simply by zeros everywhere.

Then I write down 5 at location i and 7 at location j, after which I read from k and check if it is 5 or not. Then it can be extended using the definition for something that says, for example: “if k is equal to i and k is equal to y, while k is different from j, then yes it will be 5, otherwise it will not be equal five".
And in practice, SMT solvers do not simply extend this to a variety of Boolean formulas, they use this strategy of moving back and forth between the SAT – solver and the engine, which is able to reason about array theory for the implementation of this work.
It is important that by relying on this theory of arrays, using the same strategy we used to generate formulas for integers, you can actually generate formulas that include array logic, array updates, array axes, and array iteration. And as long as you fix your way, these formulas are very easy to generate.
If you do not correct your paths, but you want to create a formula that corresponds to the passage of the program through all paths, then this is also relatively easy. The only thing you have to deal with is the special kind of cycles.
Dictionaries and maps are also very easy to model using undefined functions. Actually, the array theory itself is just a special case of an undefined function. With such functions, more complex things can be done. In today's SMT solver, there is built-in support for reasoning about sets and set operations, which can be very useful if you reason about a program that includes the calculation of sets.
When designing one of these tools, the modeling stage is very important. And it's not just how you model complex software functions down to your theories, for example, things like dropping heaps to arrays. The point is also what theories and solvers you use. There are a large number of theories and solvers with different relations, for which it is necessary to choose a reasonable compromise between efficiency and cost.

Most practical tools adhere to the theory of bit vectors and, if necessary, can use array theory to simulate a heap. In general, practical tools try to avoid more complex theories, such as set theory. This is because they are usually less scalable in some cases, if you are not dealing with a program that really requires these kinds of tools to work.
Audience: besides the study of symbolic performance, what are the developers focusing their attention on?
Professor:Another very active area of research is applications and the search for software models that will identify new types of errors. So, for example, Nikolai, Franz, and Si Wan, at last year’s lectures, considered using symbolic execution for programs that could not be optimized with the help of the compiler. This concerned security checks that can be optimized without a compiler.
Thus, it is very different from the question of whether the program will go this way or not. But there is a modeling step that allows you to move from a high-level conceptual question, whether there is code in your program that can be compiled, to an algorithm based on symbolic execution that can easily determine whether a program can follow a particular path and whether such a specific path is possible.
It turns out that applications are a large area, expanding to new classes of errors, to new features of different programming languages. For example, one of the things that is still quite difficult to model using symbolic execution is a very high level languages, such as JavaScript or Python, where you have many very dynamic language functions. But at the same time, almost any program can be adapted for symbolic execution, and this is definitely very good.

A couple of years ago we had jobs that use symbolic execution for reasoning about errors in Python programming tasks. Thus, in the case of symbolic execution, part of the problem is that your character state does not allow you to simply say: “OK, I will execute this instruction, and then this instruction, and then this instruction”. There is no sequence.
For example, several years ago we looked at very small snippets of code, but very responsible ones, containing a matching data structure inside the operating system, or an unlocked data structure, or simulating the interaction between threads.
Basically, every time there is a variable that can be overwritten by some other value, you only replace its value with a new character value and create constraints that relate to these character values and character values in other threads.
This was even used to talk about things like missing memory boundaries, while the complexity grows quite insignificantly. Relatively speaking, what you can no longer do on the Microsoft Word scale, you can do on the scale, for example, of a parallel data structure.
There were other works in the context of parallelism, for example, is it possible to use symbolic execution to reconstruct misinterpretation based on knowledge of how the program behaved while doing so.
This opens up many opportunities, as it allows you to ask specific questions about the path of the program. Symbolic execution allows you to ask what values these things should have in order for the program to do something, or for something to happen. This is a very powerful feature, and there are many applications that have been tested on its basis. But this is quite a new technology, as is the technology for analyzing program execution.
Full version of the course is available here .
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr's users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps until December for free if you pay for a period of six months, you can order here .
Dell R730xd 2 times cheaper? Only here2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?
