Programming languages. Compositional look
Hello, Habr! Today I would like to raise the question of the use of compositions and their role in programming. Those who have come across functional languages have most likely heard about them, and those who have not come across may learn something new. I hope for an interesting discussion at the end of the article on their application. Escher to attract attention.

Let's start with the concept of a program. From a mathematical point of view, a program is a function. Sometimes this may not seem obvious. If the program is a function, then you should decide what its arguments are and what it returns. In the case of simple utilities like bc, everything is clear: the argument is an expression from stdin , and the result is the result in stdout. In more complex cases, you can also come to the conclusion that the program is a function. Consider, for example, the DBMS, in this case the program is also a function, with an argument it takes the memory allocated to it in user-space , and returns it, while continuously executing. Maybe a rather suboptimal example, but it is understandable.
If the program is a function, then you should consider what means of obtaining this function can be. It all depends on programming languages, they are such tools. And regardless of whether it is a functional language, procedural, imperative, declarative, etc., all of them tend to use compositions, explicit or implicit. The time has come to define the concept of composition. Let two functions be given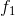 and
and  , from them we can construct a function
, from them we can construct a function applying to them the function
applying to them the function 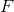 :
: ) . Such a function F, which takes other functions as an argument, will be called a composition . And there
. Such a function F, which takes other functions as an argument, will be called a composition . And there  can be many ways to build , each way - composition. Consider a couple of sample compositions: branching composition and superposition composition.
can be many ways to build , each way - composition. Consider a couple of sample compositions: branching composition and superposition composition.
Branch composition . Let two functions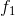 and be given
and be given  , as well as one predicate
, as well as one predicate  (the same function, but returning not the element of the set on which it is defined, but the values “true” or “false”). There is such a function
(the same function, but returning not the element of the set on which it is defined, but the values “true” or “false”). There is such a function  that
that 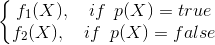 . In this case, they say that the function is
. In this case, they say that the function is  obtained by the branch operation, we denote this operation as
obtained by the branch operation, we denote this operation as  , then
, then) . Applying the composition to the functions, you can get a new function, which is then used.
. Applying the composition to the functions, you can get a new function, which is then used.
Superposition composition . Let a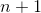 function be given
function be given  , where
, where 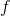 is an
is an 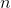 -ary function and there exists a function
-ary function and there exists a function 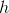 that is defined as
that is defined as ,f_2(X),...f_n(X))) . In this case
. In this case 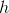 it would be considered obtained by superposition operations
it would be considered obtained by superposition operations 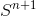 :
: ) .
.
Consider the prototypes of these operations in programming languages. Somewhere they are more explicit, somewhere less. In C, the branch operation is obviously hidden in the control structure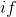 :
: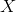 , for example, the entire set of variables in scope. In LISP, the prototype of this composition would look like this:
, for example, the entire set of variables in scope. In LISP, the prototype of this composition would look like this:
It should immediately be noted that the arity of all the proposed functions should be unified, otherwise the application of the composition mechanism to them can be significantly difficult, i.e. X is actually something like .
.
Obviously, the compositions are deeply “buried” in the syntax of programming languages, implicitly present in them. However, there is nothing new, as a sophisticated reader can rightly notice. Even Edsgar Dijkstra noticed this in his book Discipline of Programming.
In connection with the foregoing, many questions arise. In particular, why are the compositions not used explicitly? Indeed, the use of compositions explicitly could bring many advantages. Especially that it will become possible to consider the programming process itself, and therefore to optimize the development of complex projects. After all, how is the programmer programming now? He does this as an artist painting a picture. In other words, design decisions are made on the basis of his experience, premonition, the advice of colleagues, some personal aesthetic beliefs. But this line of thought cannot be simply put into a file with the program. Those. There is a program, but there is no train of thought that led to it. This is the first question. Why do languages have such syntax, why did the creators of the language lay such a set of control structures? Why is their set dogmatized? What to do if you need to add other control structures.
These questions would help to solve the means of application and generation of compositions. Since the solution of any arbitrarily complex task by a person is reduced to analysis / decomposition, and then synthesis, this process can be organically supported by the composition mechanism. After all, compositions will be precisely the connecting element that will glue together the parts into which the task is divided. Well, a person will have to break the task one way or another, it is precisely his prerogative, and not the syntactic design of the task. Unfortunately, not a single language that has been tailored to the concept of composition has been noticed so far.
For a better understanding, consider the example of finding the largest common divisor (GCD) using compositions. The calculator can find the remainder of the division ( ), perform integer division (
), perform integer division (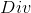 ), calculate the inequality predicate (
), calculate the inequality predicate ( 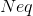 ), generate zero (
), generate zero (  ). All functions are defined on the set of natural numbers without zero. We thus have the following functions in the proposed algebra
). All functions are defined on the set of natural numbers without zero. We thus have the following functions in the proposed algebra  = {
= { 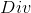 ,
,  ,
,  ,
, 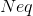 ,
, 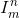 }. The reader may notice another function - the
}. The reader may notice another function - the 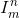 so-called selector function, which of the
so-called selector function, which of the 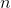 arguments returns without changing the
arguments returns without changing the 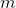 -th, it is necessary, since we work with
-th, it is necessary, since we work with 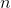 -ary functions. In addition, a cycling composition is available, let's call it
-ary functions. In addition, a cycling composition is available, let's call it  . We give its definition. Let given are
. We give its definition. Let given are 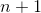
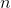 -ary functions
-ary functions  , as well as
, as well as 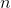 -ary predicate
-ary predicate . Iteratively, each function calculates one of the arguments for the next iteration, it
. Iteratively, each function calculates one of the arguments for the next iteration, it 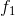 calculates
calculates 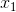 ,
,  calculates
calculates  , etc. The iterative process continues until the value of the predicate is true. The arguments to the loop operation are passed in the following order
, etc. The iterative process continues until the value of the predicate is true. The arguments to the loop operation are passed in the following order ) . The value
. The value 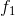 obtained at the last iteration
obtained at the last iteration  will be the value of the function resulting from the composition. In addition, a composition of superposition, as previously described, is available. Then the GCD calculation algorithm can be written as
will be the value of the function resulting from the composition. In addition, a composition of superposition, as previously described, is available. Then the GCD calculation algorithm can be written as ,S^3(Div, I^3_3, I^3_2),S^3(Rem, I^3_3, I^3_2), I^3_2), I^2_1, I^2_2, I^2_1)) . Schematically, it will look as follows:
. Schematically, it will look as follows:
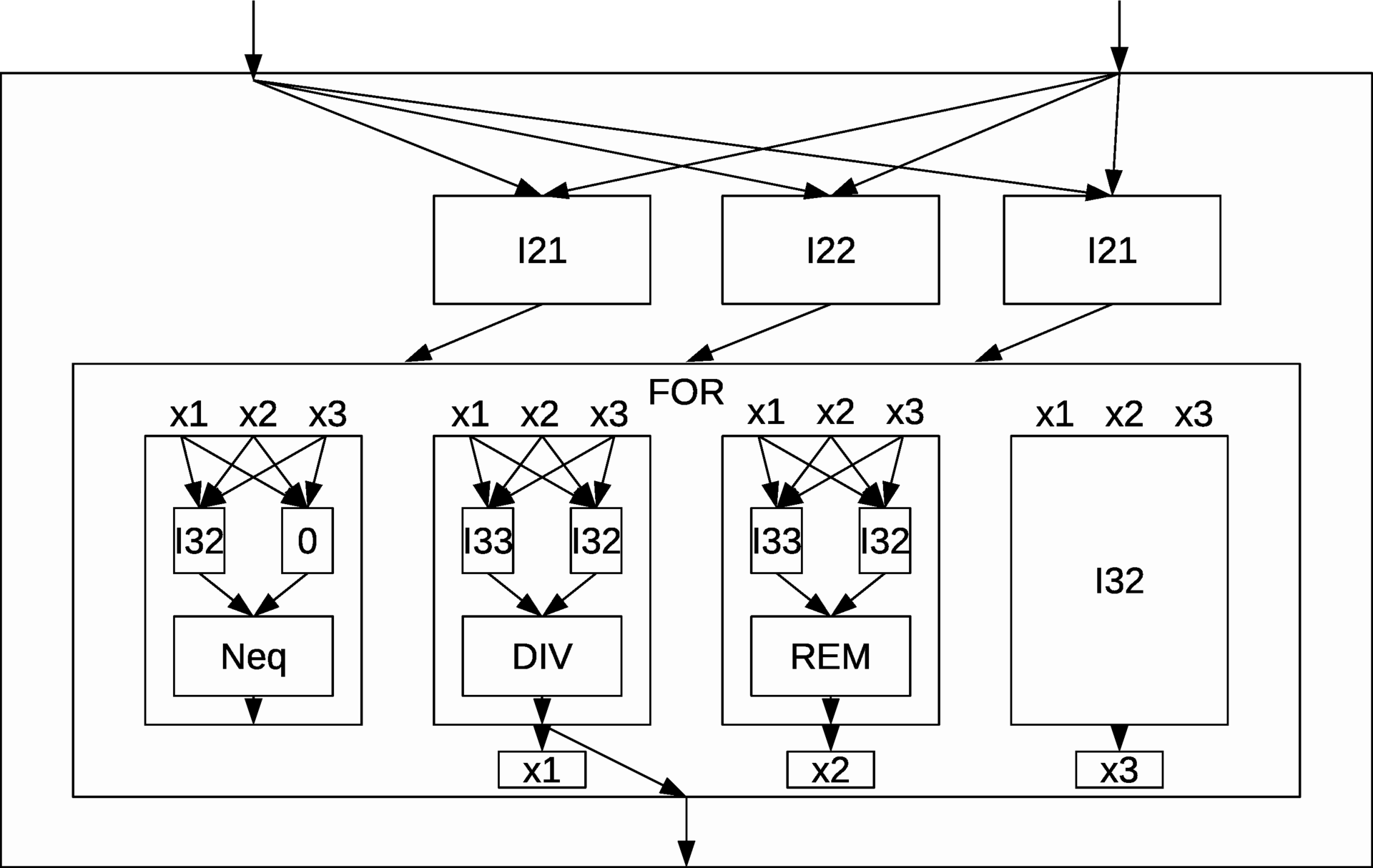
Thus, it becomes possible to formalize the algorithm itself with the “language of mathematics”, which means that it can be studied by mathematical means, which makes it possible to reduce the proportion of unreasonable or unconsciously accepted design decisions due to the fact that a person thinks in terms of the programming language he writes in instead of to reflect on compositions that, in fact, underlie various languages.
The compositional approach to the solution itself was investigated by A.I. Maltsev (Maltsev algebras), academician Glushkov (algorithmic algebras). But they all work at the level of application of compositions, dogmatizing the set of compositions with which work is being conducted. An important improvement in the compositional approach would be the ability to obtain new compositions from existing ones by applying some meta-compositions to them. The topic is interesting, I don’t know that anyone would touch it, but more about that next time. I hope I did not bore you.
The foregoing is the subject of my research. I will immediately make a remark that the compositional approach is not proposed for use for trivial calculations, like the same GCD algorithm, or in projects where the proportion of calculations is negligible. I really want to know what the community believes. Does the compositional approach have a future? Would you like to practice compositions? Do you need tools for this?
PS Suddenly I saw a recent post , which also touched on the theme of compositions. I hope they complement each other.
PPS Many thanks to sekrasoft for helping me fix the article.

Let's start with the concept of a program. From a mathematical point of view, a program is a function. Sometimes this may not seem obvious. If the program is a function, then you should decide what its arguments are and what it returns. In the case of simple utilities like bc, everything is clear: the argument is an expression from stdin , and the result is the result in stdout. In more complex cases, you can also come to the conclusion that the program is a function. Consider, for example, the DBMS, in this case the program is also a function, with an argument it takes the memory allocated to it in user-space , and returns it, while continuously executing. Maybe a rather suboptimal example, but it is understandable.
If the program is a function, then you should consider what means of obtaining this function can be. It all depends on programming languages, they are such tools. And regardless of whether it is a functional language, procedural, imperative, declarative, etc., all of them tend to use compositions, explicit or implicit. The time has come to define the concept of composition. Let two functions be given
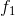 and
and  , from them we can construct a function
, from them we can construct a function applying to them the function
applying to them the function 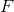 :
: ) . Such a function F, which takes other functions as an argument, will be called a composition . And there
. Such a function F, which takes other functions as an argument, will be called a composition . And there  can be many ways to build , each way - composition. Consider a couple of sample compositions: branching composition and superposition composition.
can be many ways to build , each way - composition. Consider a couple of sample compositions: branching composition and superposition composition. Branch composition . Let two functions
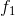 and be given
and be given  , as well as one predicate
, as well as one predicate  (the same function, but returning not the element of the set on which it is defined, but the values “true” or “false”). There is such a function
(the same function, but returning not the element of the set on which it is defined, but the values “true” or “false”). There is such a function  that
that 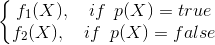 . In this case, they say that the function is
. In this case, they say that the function is  obtained by the branch operation, we denote this operation as
obtained by the branch operation, we denote this operation as  , then
, then) . Applying the composition to the functions, you can get a new function, which is then used.
. Applying the composition to the functions, you can get a new function, which is then used. Superposition composition . Let a
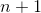 function be given
function be given  , where
, where 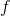 is an
is an 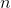 -ary function and there exists a function
-ary function and there exists a function 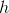 that is defined as
that is defined as ,f_2(X),...f_n(X))) . In this case
. In this case 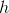 it would be considered obtained by superposition operations
it would be considered obtained by superposition operations 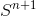 :
: ) .
. Consider the prototypes of these operations in programming languages. Somewhere they are more explicit, somewhere less. In C, the branch operation is obviously hidden in the control structure
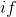 :
:if(p(X)) f1(X); else f2(X);p(X) ? f1(X) : f2(X);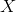 , for example, the entire set of variables in scope. In LISP, the prototype of this composition would look like this:
, for example, the entire set of variables in scope. In LISP, the prototype of this composition would look like this:(if (p X) (f1 X) (f2 X))if p X then f1 X else f2 Xg x
| p x == True = f1 x
| p x == False = f2 xf(f1(X), f2(X), f3(X));(f (f1 X) (f2 X) (f3 X))f (f1 x) (f2 x) (f3 x)It should immediately be noted that the arity of all the proposed functions should be unified, otherwise the application of the composition mechanism to them can be significantly difficult, i.e. X is actually something like
 .
. Obviously, the compositions are deeply “buried” in the syntax of programming languages, implicitly present in them. However, there is nothing new, as a sophisticated reader can rightly notice. Even Edsgar Dijkstra noticed this in his book Discipline of Programming.
Using Songs
In connection with the foregoing, many questions arise. In particular, why are the compositions not used explicitly? Indeed, the use of compositions explicitly could bring many advantages. Especially that it will become possible to consider the programming process itself, and therefore to optimize the development of complex projects. After all, how is the programmer programming now? He does this as an artist painting a picture. In other words, design decisions are made on the basis of his experience, premonition, the advice of colleagues, some personal aesthetic beliefs. But this line of thought cannot be simply put into a file with the program. Those. There is a program, but there is no train of thought that led to it. This is the first question. Why do languages have such syntax, why did the creators of the language lay such a set of control structures? Why is their set dogmatized? What to do if you need to add other control structures.
These questions would help to solve the means of application and generation of compositions. Since the solution of any arbitrarily complex task by a person is reduced to analysis / decomposition, and then synthesis, this process can be organically supported by the composition mechanism. After all, compositions will be precisely the connecting element that will glue together the parts into which the task is divided. Well, a person will have to break the task one way or another, it is precisely his prerogative, and not the syntactic design of the task. Unfortunately, not a single language that has been tailored to the concept of composition has been noticed so far.
For a better understanding, consider the example of finding the largest common divisor (GCD) using compositions. The calculator can find the remainder of the division (
 ), perform integer division (
), perform integer division (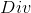 ), calculate the inequality predicate (
), calculate the inequality predicate ( 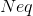 ), generate zero (
), generate zero (  ). All functions are defined on the set of natural numbers without zero. We thus have the following functions in the proposed algebra
). All functions are defined on the set of natural numbers without zero. We thus have the following functions in the proposed algebra  = {
= { 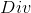 ,
,  ,
,  ,
, 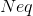 ,
, 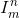 }. The reader may notice another function - the
}. The reader may notice another function - the 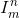 so-called selector function, which of the
so-called selector function, which of the 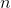 arguments returns without changing the
arguments returns without changing the 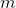 -th, it is necessary, since we work with
-th, it is necessary, since we work with 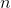 -ary functions. In addition, a cycling composition is available, let's call it
-ary functions. In addition, a cycling composition is available, let's call it 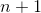
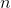 -ary functions
-ary functions  , as well as
, as well as 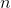 -ary predicate
-ary predicate . Iteratively, each function calculates one of the arguments for the next iteration, it
. Iteratively, each function calculates one of the arguments for the next iteration, it 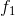 calculates
calculates 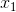 ,
,  calculates
calculates  , etc. The iterative process continues until the value of the predicate is true. The arguments to the loop operation are passed in the following order
, etc. The iterative process continues until the value of the predicate is true. The arguments to the loop operation are passed in the following order  obtained at the last iteration
obtained at the last iteration 
Thus, it becomes possible to formalize the algorithm itself with the “language of mathematics”, which means that it can be studied by mathematical means, which makes it possible to reduce the proportion of unreasonable or unconsciously accepted design decisions due to the fact that a person thinks in terms of the programming language he writes in instead of to reflect on compositions that, in fact, underlie various languages.
The compositional approach to the solution itself was investigated by A.I. Maltsev (Maltsev algebras), academician Glushkov (algorithmic algebras). But they all work at the level of application of compositions, dogmatizing the set of compositions with which work is being conducted. An important improvement in the compositional approach would be the ability to obtain new compositions from existing ones by applying some meta-compositions to them. The topic is interesting, I don’t know that anyone would touch it, but more about that next time. I hope I did not bore you.
The foregoing is the subject of my research. I will immediately make a remark that the compositional approach is not proposed for use for trivial calculations, like the same GCD algorithm, or in projects where the proportion of calculations is negligible. I really want to know what the community believes. Does the compositional approach have a future? Would you like to practice compositions? Do you need tools for this?
PS Suddenly I saw a recent post , which also touched on the theme of compositions. I hope they complement each other.
PPS Many thanks to sekrasoft for helping me fix the article.
