We write a converter for the ringtone generator from Nokia 3310

Fans of all the old, but insanely interesting, good evening!

Remember this phone - Nokia 3310? Remember, of course! And such a thing as a melody synthesizer in it? Also remember, great. Do you miss old, warm and lamp melodies? So I miss. And I came across a website with more than a hundred sheet music for this editor. And that I had to leave this charm without attention? No, really. What I've done? Right! I took and wrote exactly the same melody generator, which allows you to get a Wave - file with a melody at the output. I wonder what came of it? Then I ask for cat.

Nokia Composer was built into a whole bunch of phones like the Nokia 3310. In addition to 7 notes, it allowed you to record 5 sharps, specify an octave and duration in parts. And there were notes that didn't sound - pauses. That is, the “note” in Composer was really a note.

The very record of the note for Composer looked like this:



That is, in the beginning there is a duration (in parts of the whole), then there could be a dot extending the sound by one and a half times, the note itself in the letter designation, and an octave . In this case, after a pause, the octave is not indicated (is it logical?), And the duration is indicated exactly the same as for a normal note.

Okay, talk.

Let's write a script that will take a note as it is and return a tuple of parameters.

(writing in Python 2.7, yes)

def Parse_Tone(Note):
	Note = Note.upper()
	if Note.find("-") == -1:
		try:
			(Duration, Octave) = re.findall(r"[0-9]+", Note)
		except:
			pass
	else:
		Duration = re.findall(r"[0-9]+", Note)[0]
		Octave = 1
	Tone = re.findall(r"[A-Z,#,-]+", Note)[0]
	Duration = int(Duration)
	Octave = int(Octave)
	if Note.find(".") != -1:
		Duration = Duration/1.5
	return (32/Duration, Tone, Octave)

In! That is, first we translate it into the UPPER REGISTER, and then - using regular expressions we parse it into components. Separately, check for a point (increase by 1.5 times) and take into account the pause.

Gototo!
Now, if we transfer functions, for example, 16C2, we get (2, C, 2) at the output, that is, the duration in shares, note and octave.

What? Where did the number 32 come from? It’s just
Original Nokia Composer let you set the duration of a note as 1/32 of a “full” note. Moreover, for him there are also 1/16, 1/8, 1/4, 1/2 and 1 duration. That is, each next duration differs from the previous one exactly 2 times. Then we can do this:

Take 1/32 notes as a “single note”. Then 1/16 is already 2 single notes, 1/8 - 4 and so on. Then we can take and divide 32 by the received duration.

We figured it out. Now it remains to understand how we will turn this whole thing into a Wav file.

If it’s very rough - in the Wave file, in addition to the header, the voltages that are supplied to the speaker are recorded. If a little more precisely - part of the voltage from the maximum . That is, if the number 32765 is written in a two-byte frame, this means that you need to apply the maximum voltage. By changing stress levels over time, we can achieve vibrations of the speaker membrane. And if these fluctuations are in the range we need ... That's right! We will hear a sound of a certain frequency.

Now, how to do it.

Let's strain the memory and ... remember the school physics course! About the part that talks about harmonic vibrations .

If it’s very simple: harmonic oscillations are a type of oscillations whose oscillating value changes according to the law of sine (well, or cosine, as you want).



The general formula of this disgrace looks like: Did



you



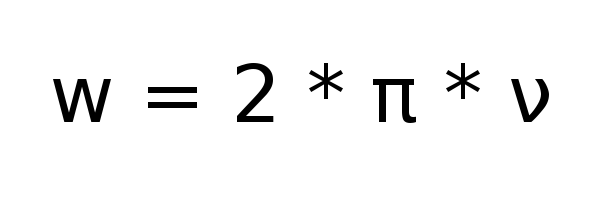
remember this cyclic frequency ? Excellent! Now you need to understand - why.

Since we decided to set the sound as a change in the voltage across the speaker, we will set the changes as a sinusoid with the cyclic frequency we need (by the way, the most obvious way to create sound). In this case, the formula for calculating the amplitude of the current frame will look like

Result = (32765 * VOL * math.sin (6.28 * FREQ * i / 44100))

Where did all this come from? I tell you.

32765 - We have a two-byte frame, so the maximum amplitude value is exactly 32765. VOL is a variable that sets the volume. Changes in the range from 0 (complete silence) to 1 (yelling as if on an area)

6.28 - this is just 2 * Pi. You can calculate each time, but we are not animals.

FREQ - And this is what everything was started for - the frequency we need.

i / 44100 - time, relative to the origin. Why are we dividing by 44100? But because this is the sampling rate of the output file (well, I thought of it that way. Maybe less. The quality will be lower). There are 44100 readings per second, therefore we divide. I hope it turned out to explain

Here you go. We learned to set one frame. Now you need to make it all work. That is, in addition to the frequency, also set the duration.

And since the frequency is fixed ... Yeah! Wrap it in a loop.

Here in this one.

for i in range(0,TIME/10*441):
		Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
		Frames.append(Result)

Again incomprehensibility. Where did TIME / 10 * 441 come from ? From my imagination. No seriously. This is how I decided that the minimum playing time is 0.001 second . As I already said - one sample (at a given sampling frequency) is 1/44100 seconds. Accordingly, 0.001 second is 44.1 counts. A 44.1 = 441/10. And if you need to set N milliseconds ... multiply, yeah. So we get what we wrote (TIME is just the same time in milliseconds, yes)

So well, let's wrap this whole thing up a function, I hope no one is against it?

def Append_Freq(VOL,FREQ, TIME):
	for i in range(0,TIME/10*441):
		Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
		Frames.append(Result)

In! Now we can generate sound of absolutely any frequency.

It remains to record what happened in the wave - file.

To work with Wave in Python (at least 2.7) there is an attractive module with an unforgettable name - Wave . And to work with all sorts of structures - struct (in general, up to a certain point, Python is an insanely logical language).

After some dances with a tambourine and other perversions, we got this function:

def Write_Wave(Name):
	File = wave.open(Name, 'w')
	File.setparams((1, 2, 44100, 0, 'NONE', 'not compressed'))
	Result = []
	for frame in Frames:
		Result.append(pack('h', frame))
	for Each in Result:
		File.writeframes(Each)

(I won’t talk about it, because, firstly, everything is clear, and secondly, we won’t move away from the topic)

Well. Now you can generate a sound!
We try.

Frames = []
Append_Freq(1, 4000, 5000)
Write_Wave('Sound.wave')

Full volume, 4 kilohertz, 5 seconds.
Let's see what happened?

This is how it sounds:

5000Hz.wav

And it looks like this:



Well, in general, what they wanted was what they got. The sound is really rather unpleasant.

By the way, if my memory serves me right, that in the old library for Turbo Pascal the sound was set not by a sinusoid, but by a meander. In fact, just changing the voltage across the speaker is enough. Just a sine wave prettier than a meander or saw.

Here you go. Now we have a function that generates sound of the desired frequency and duration and a function that records what we have done in this file.

Now you need to learn how to record notes.

A clean (not instrumentally colored) note is the sound of a certain frequency.

A sharp note is a sound with a frequency one and a half tones higher than a clean note.

Be - mole is a sound with a frequency one and a half tones lower than a clean note . Do not pray the original Composer (still remember what we wanted to write there? Excellent!) Does not allow to set, therefore we will not work with be - moles. Well them.

Octave - if simplified, it's a note frequency multiplier . That is, the frequency Re of the second octave is twice as high as the same Re of the first octave.

Find a table of notes and their frequencies on the Internet



and make a dictionary out of it.

Here is one:

Notes = {"-" : 0 ,"C" : 261.626, "#C" : 277.183, "D" : 293.665, "#D" : 311.127, "E": 329.628, "#E" : 349.228, "F" : 349.228, "#F" : 369.994, "G" : 391.995, "#G" : 415.305, "A" : 440.000, "#A" : 466.164, "B" : 493.883, "#B" : 523.251}

(In general, it is probably more correct to write C # rather than #C, but as a rule all the tunes for Composer were indicated in this format)

And now we will write another function that generates the sound of a certain note

def Append_Note(VOL, TIME, NOTE, OCTAVE):
	for i in range(0,int(TIME/10.0*441)):
		FREQ = Notes[NOTE]*OCTAVE
		Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
		Frames.append(Result)
		#making clear sound
	if (abs(math.sin(6.28*FREQ*i/44100))>0.01):
		while (abs(math.sin(6.28*FREQ*i/44100))>0.01):
			Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
			Frames.append(Result)
			i+=1

So, there’s something else to say.

With the first part, everything is clear - the value of the desired frequency is taken from the dictionary, multiplied by an octave and written to the list.

Why do we need a second?

Very simple. If the desired duration is not a multiple of the sine wave period, then at time T1 a large voltage can be applied to the speaker, and nothing will be supplied to T1 + 1 . To my bear’s ears, it sounds like a suddenly broken phrase of a murdered comrade — unpleasant. Therefore, we bring our sine wave to the nearest zero. At a high sampling rate, this will be noticeably small, but by ear it will look like the same clipping phrase of a friend, if the deceiving (but yelling) friend falls into the well. It’s also not God knows what, but for the generation of Nokiev melodies it will do.

Now it remains to write a function that will take a list of notes and feed it to the generator element by element.

def Append_Notes(VOL, LIST, BPM):
	for Each in LIST:
		(Duration, Tone, Octave) = Parse_Tone(Each)
		try:
			Append_Note(VOL, int(Duration*1000*7.5/BPM), Tone, Octave)	
		except:
			print "Ошибка! Не могу обработать %s" %Each
		Append_Note(0, int(250*7.5/BPM), "-", 1)

Something like this.

Is something incomprehensible again? This is normal, I don’t understand anything either , now we’ll figure it out.

BPM is the number of beats per minute. Roughly speaking, this is the "speed of the game." This BPM is equal to the number of quarter notes in one minute . That is, one quarter note should be played 60 / BPM seconds. And since, we decided that the duration of a single note with us is 1/32 - this value is 60/32 * 4 / BPM = 7.5 / BPM . One quarter note sounds exactly 1000 milliseconds (for some reason the composers came up with this), and then this result is also multiplied by the number of such 1/32 notes.

When the function completes, the finished list appears in the Frame list , which remains to be written.

Well, and since I'm too lazy to write GUIs, I like console interfaces, we write a note sequence handler that takes this sequence, BPM and the name of the output file in the argument list and feeds the functions Append_Notes ()

def MakeTune():
	if (len(Arguments)!=3):
		print 'ERROR!\n	USAGE:\n	Composer "Notes" BMP FileName\nExample:\n	Composer "16c2 16#a1 4c2 2f1 16#c2 16c2 8#c2 8c2 2#a1 16#c2 16c2 4#c2 2f1 16#a1 16#g1 8#a1 8#g1 8g1 8#a1 2#g1 16g1 16#g1 2#a1 16#g1 16#a1 8c2 8#a1 8#g1 8g1 4f1 4#c2 1c2 16c2 16#c2 16c2 16#a1 1c2" 120 Music.wave'
		return 1
	List = Arguments[0].split(' ')
	BPM = int(Arguments[1])
	OutFile = Arguments[2]
	print "\nFile information:\n\n	Note number: %s\n	Tempo: %s BPM\n\nGeneration of amplitude..." % (len(List), BPM)
	Append_Notes(1, List, BPM)
	print "\nOk!\n\nWriting Wave File..."
	Write_Wave(OutFile)
	File = open(OutFile,'rb').read()
	Size = len(File)
	print "\n	File size: %.2f MB\n	Duration: %.2f c. \n\nAll Done." % (Size/1024.0/1024, Size/44100/2)

That's all.

Now it remains only to transfer the source data to the program and pick up the finished melody.

Will we try?



We drive it into the generator ...



And we take the result:

output.wav

In my opinion, not bad.

More examples? Easy!

Anthem of the USSR
Under the blue sky
Autumn
Christmas melody (from the original 3310)

Do you want to write yourself? Give it a try!



Here's the pace: 200

Skip through the generator and see what happens (And someone may know by eye).

Generator Script

I hope you enjoyed it!

Sincerely yours, listening to monophonic Mozart, GrakovNe