How not to calculate the matrix exponent
The post was written under the influence of the post of the user pchelintsev_an .
In this article I will try to tell you what computational difficulties you may encounter if you go along the “naive” way of calculating the matrix exponent. The article may be useful to those who would like to get acquainted with computational mathematics, but are already familiar with such concepts as a system of ordinary differential equations and the Cauchy problem. The experiments were carried out using the GNU Octave system .
A matrix exponent arises when considering the Cauchy problem for a linear system of ordinary differential equations with constant coefficients:
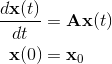
Sometimes such systems arise after partial discretization of partial differential equations, for example, in finite element methods. Then the matrix A is some finite-dimensional approximation of the differential operator. As a result, the number of rows of matrix A can easily reach thousands, millions, and even several billion. Such matrices cannot even be stored in the form of a square array; therefore, they are stored in special sparse presentation formats.
The solution to the ODE system can be written out explicitly:
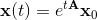
A matrix exponent appears here, which is defined as the sum of the series:
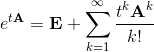
In fact, the matrix exponent is obtained by formal substitution of the matrix A into the Taylor series for e z (the mathematician will note that the series converges absolutely for any matrix and any t ). Conveniently, using the matrix exponent, you can calculate the solution at any time t. For example, if this system is solved by some method of numerical integration, for example, Adams or Runge-Kutta , then the time spent will be proportional to time t. However, a solution through a matrix exponent is possible only for autonomous systems with constant coefficients.
In the course of differential equations for practical calculations of the matrix exponent, a method for reducing the matrix to Jordan form is proposed: if the matrix A is represented in the form SJS -1 , where J is the Georges form, S is the matrix of the transition to the Jordan basis, then the matrix exponent A is expressed through the matrix exponent J: The
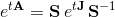
matrix exponent from the Jordan matrix J is written in explicit form. However, this method requires computing a system of eigenvectors, as well as vectors attached to them. This task is much more complicated than the initial one. Moreover, even for a real matrix A, its Jordan form J can be complex.
So, we have an infinite series and the desire to calculate it in the foreseeable time. The obvious way is to end the summation on some term by discarding the remainder. Moreover, the summation of the series ends if the next kth term in the norm is small:
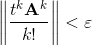
Let us dwell briefly on the norm of the matrix. There are a lot of different matrix norms. We can introduce a norm based on the requirement.
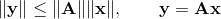
In this case, we speak of the norm of the matrix induced (or subordinate) to some vector norm. For the most used vector norms, the corresponding matrix norms have the form:
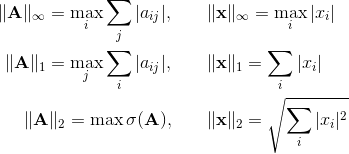
The first two norms of the matrix are considered elementary, and for the latter it is required to calculate a singular number, which is very difficult. In addition to the induced norms, there are a number of other norms. The Frobenius norm is practically convenient, which, on the one hand, is easy to calculate, and on the other hand, it is closely related to the singular numbers A. In fact, this is the Euclidean norm of the vector obtained by “pulling” the matrix into one row:
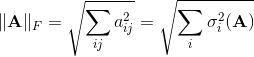
To understand the difficulties that arise when summing up Taylor series, it is not necessary to refer to the example with a matrix exponent. Let's just try to plot the function e -x on the interval [0, 50], summing up the Taylor series for the exponent in the same way. We complete the summation if the next term does not exceed 10 -20 . We will use the following code on Octave:
The result is rather strange:
For x> 30, the function graph starts to behave randomly and has nothing to do with the exponent.
The reason for this effect is the accumulation of rounding errors. For example, when calculating e -35 , 132 terms were added up, of which the last term had a minimum of the absolute value s 132 ≈ 5.8674 · 10 -21 , and the term number 35 had a maximum of the absolute value: s 35 ≈ -1.067 · 10 14 . Since Octave performs calculations with double precision (approximately 16 significant digits), rounding of the 35th term has already introduced an error of the order of 0.01, which significantly exceeds both the value ϵ = 10 -20 and the value of the sum of the series e-35 ≈ 6.305 · 10 -16
Is the Taylor series so hopeless? No, rounding errors will not make a significant contribution if the summed terms do not reach such huge values. For example, such an algorithm will work reliably for small values of x (| x | ≲ 1). For the matrix exponent, a similar condition has the form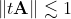 . In addition to computational stability, such a choice of x provides fast convergence, that is, it is enough to take only a few terms from the series to obtain acceptable accuracy.
. In addition to computational stability, such a choice of x provides fast convergence, that is, it is enough to take only a few terms from the series to obtain acceptable accuracy.
Note that the matrix exponent satisfies the following relation:
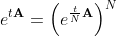
This means that the matrix exponent can be calculated for the matrix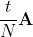 , and then the result can be raised to the power N. Taking as N = 2 p, you can use the fast algorithm for raising to the power in p matrix multiplications:
, and then the result can be raised to the power N. Taking as N = 2 p, you can use the fast algorithm for raising to the power in p matrix multiplications:
The number p can (and should) be chosen for reasons of computational stability of step 1 of the algorithm, i.e., the
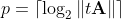
Corresponding Octave code:
A segment of a Taylor series is not the only way to approximately calculate the value of a function. Better approximations of the function can be obtained not in the form of polynomials, but in the form of rational functions. The best approximations in the form of the ratio of two polynomials of given degrees are called Padé approximants . For example, the Padé approximation by the ratio of two quadratic polynomials for the exponent is written as:
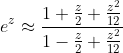
A similar approximation for the matrix exponent will be:
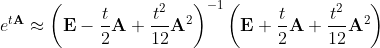
Padé approximants can be used for step 1 in the doubling algorithm. The main difficulty associated with Padé approximations is the need to invert the matrix once. For large matrices, this can be quite time consuming.
How to make sure that the matrix exponent is calculated correctly? Is it enough that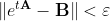 a more “intelligent” check is required?
a more “intelligent” check is required?
Recall that the matrix exponent arose not out of the blue, but as a result of solving a system of ordinary differential equations. The eigenvalues of the matrix A characterize the rates of the processes occurring in the system described by this system of differential equations. For example, the matrix:
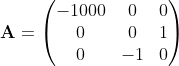
describes a system with one rapidly decaying process (eigenvalue -1000) and two oscillatory processes (eigenvalues ± i ). A good criterion for the correctness of the calculation of the matrix exponent can be the relation:
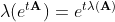
connecting the eigenvalues of the matrix A and its matrix exponent.
To begin, we study the performance algorithms on random matrices of different sizes. As methods, we use the method of summing the Taylor series, the method of doubling the argument, and the expm function built into Octave . Initially, I also wanted to compare the correspondence of the eigenvalues, but I had to abandon this idea, since all three algorithms equally failed this check with the size of the matrix N ≳ 50. Perhaps the culprit was the function of determining the eigenvalues eig , which does not work accurately or the conditionality of the problem of determining the eigenvalues itself values for these matrices.
Based on the graph, the doubling method works approximately twice as long as the library function (it may be worth loosening the overestimated accuracy requirement), while direct summation even has a different asymptotic behavior ≈O (N 3.7 ), while the rest have the asymptotic behavior O (N 3 ).
Next, let’s check how the algorithm works with large eigenvalues. Consider the following system of ordinary differential equations
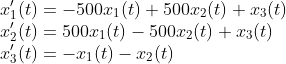
with the initial conditions:
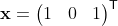 .
.
Its peculiarity is that one of its eigenvalues is -1000 (a rapidly decaying solution), and the other two are ± i √2 (oscillatory solutions). If distortions are introduced into the imaginary eigenvalues, this will be clearly visible. Take a time step τ = 0.038, find the matrix exponent in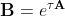 different ways. The solution of the system on a grid with a step τ is obtained by the following simple algorithm:
different ways. The solution of the system on a grid with a step τ is obtained by the following simple algorithm:
Let's look at the obtained numerical trajectories (only the first component of the vector is displayed):
All the trajectories, except those obtained by direct summation of the Taylor series, visually coincide. Note that the graph does not go beyond the initial condition x 1 (0) = 1. In fact, the graph exponentially approaches the point y = 1, just the characteristic distance of the “rotation” of the graph (∼ 1/1000) is much less than the time step τ = 0.038.
We can say that the example is synthetic, and in practice it will not occur, but this is not so. There are many so-called rigid Cauchy problems , which are characterized by a strong scatter of eigenvalues (in fact, the rates of physical processes).
The various methods of calculating the matrix exponent can be found in the article [English] [2]. A remarkable two-volume book has been written on the methods for solving ordinary differential equations and stiff problems [3,4]
In this article I will try to tell you what computational difficulties you may encounter if you go along the “naive” way of calculating the matrix exponent. The article may be useful to those who would like to get acquainted with computational mathematics, but are already familiar with such concepts as a system of ordinary differential equations and the Cauchy problem. The experiments were carried out using the GNU Octave system .
What is a matrix exponent in general and what is it used for
A matrix exponent arises when considering the Cauchy problem for a linear system of ordinary differential equations with constant coefficients:
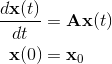
Sometimes such systems arise after partial discretization of partial differential equations, for example, in finite element methods. Then the matrix A is some finite-dimensional approximation of the differential operator. As a result, the number of rows of matrix A can easily reach thousands, millions, and even several billion. Such matrices cannot even be stored in the form of a square array; therefore, they are stored in special sparse presentation formats.
The solution to the ODE system can be written out explicitly:
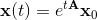
A matrix exponent appears here, which is defined as the sum of the series:
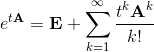
In fact, the matrix exponent is obtained by formal substitution of the matrix A into the Taylor series for e z (the mathematician will note that the series converges absolutely for any matrix and any t ). Conveniently, using the matrix exponent, you can calculate the solution at any time t. For example, if this system is solved by some method of numerical integration, for example, Adams or Runge-Kutta , then the time spent will be proportional to time t. However, a solution through a matrix exponent is possible only for autonomous systems with constant coefficients.
In the course of differential equations for practical calculations of the matrix exponent, a method for reducing the matrix to Jordan form is proposed: if the matrix A is represented in the form SJS -1 , where J is the Georges form, S is the matrix of the transition to the Jordan basis, then the matrix exponent A is expressed through the matrix exponent J: The
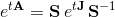
matrix exponent from the Jordan matrix J is written in explicit form. However, this method requires computing a system of eigenvectors, as well as vectors attached to them. This task is much more complicated than the initial one. Moreover, even for a real matrix A, its Jordan form J can be complex.
Row summation
So, we have an infinite series and the desire to calculate it in the foreseeable time. The obvious way is to end the summation on some term by discarding the remainder. Moreover, the summation of the series ends if the next kth term in the norm is small:
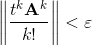
Matrix Norms
Let us dwell briefly on the norm of the matrix. There are a lot of different matrix norms. We can introduce a norm based on the requirement.
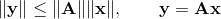
In this case, we speak of the norm of the matrix induced (or subordinate) to some vector norm. For the most used vector norms, the corresponding matrix norms have the form:
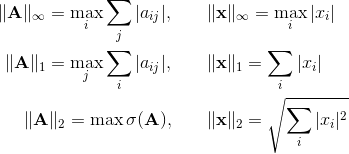
The first two norms of the matrix are considered elementary, and for the latter it is required to calculate a singular number, which is very difficult. In addition to the induced norms, there are a number of other norms. The Frobenius norm is practically convenient, which, on the one hand, is easy to calculate, and on the other hand, it is closely related to the singular numbers A. In fact, this is the Euclidean norm of the vector obtained by “pulling” the matrix into one row:
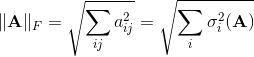
Surprises when summing up a series
To understand the difficulties that arise when summing up Taylor series, it is not necessary to refer to the example with a matrix exponent. Let's just try to plot the function e -x on the interval [0, 50], summing up the Taylor series for the exponent in the same way. We complete the summation if the next term does not exceed 10 -20 . We will use the following code on Octave:
function [y] = myexp(x, eps)
xk = ones(size(x));
y = xk;
k = 0;
do
k = k + 1;
xk = xk .* x / k;
y = y + xk;
until (max(abs(xk)) < eps)
end
x = linspace(0, 50, 2000);
y = myexp(-x, 1e-20);
plot(x, y, 'b', x, exp(-x), 'r');
axis([0 50 -0.1 1.1]);
The result is rather strange:
For x> 30, the function graph starts to behave randomly and has nothing to do with the exponent.
The reason for this effect is the accumulation of rounding errors. For example, when calculating e -35 , 132 terms were added up, of which the last term had a minimum of the absolute value s 132 ≈ 5.8674 · 10 -21 , and the term number 35 had a maximum of the absolute value: s 35 ≈ -1.067 · 10 14 . Since Octave performs calculations with double precision (approximately 16 significant digits), rounding of the 35th term has already introduced an error of the order of 0.01, which significantly exceeds both the value ϵ = 10 -20 and the value of the sum of the series e-35 ≈ 6.305 · 10 -16
Is the Taylor series so hopeless? No, rounding errors will not make a significant contribution if the summed terms do not reach such huge values. For example, such an algorithm will work reliably for small values of x (| x | ≲ 1). For the matrix exponent, a similar condition has the form
Argument Doubling Method
Note that the matrix exponent satisfies the following relation:
This means that the matrix exponent can be calculated for the matrix
- Calculate matrix exponent
- Multiply B by
repeating this operation p times
- As a result
The number p can (and should) be chosen for reasons of computational stability of step 1 of the algorithm, i.e., the
Corresponding Octave code:
function [B] = taylorexp(t, A, eps, max_terms)
B = eye(size(A));
Ak = B;
k = 0;
while norm(Ak, 'fro') > eps && k < max_terms
k = k + 1;
Ak = (t / k) * Ak * A;
B = B + Ak;
end
end
function [B] = argdbl(t, A, eps, max_terms)
p = ceil(log2(abs(t) * norm(A, 'fro')));
B = taylorexp(t / pow2(p), A, eps, max_terms);
for i = 1:p
B = B * B;
end;
end
Pade approximation method
A segment of a Taylor series is not the only way to approximately calculate the value of a function. Better approximations of the function can be obtained not in the form of polynomials, but in the form of rational functions. The best approximations in the form of the ratio of two polynomials of given degrees are called Padé approximants . For example, the Padé approximation by the ratio of two quadratic polynomials for the exponent is written as:
A similar approximation for the matrix exponent will be:
Padé approximants can be used for step 1 in the doubling algorithm. The main difficulty associated with Padé approximations is the need to invert the matrix once. For large matrices, this can be quite time consuming.
Accuracy analysis
How to make sure that the matrix exponent is calculated correctly? Is it enough that
Recall that the matrix exponent arose not out of the blue, but as a result of solving a system of ordinary differential equations. The eigenvalues of the matrix A characterize the rates of the processes occurring in the system described by this system of differential equations. For example, the matrix:
describes a system with one rapidly decaying process (eigenvalue -1000) and two oscillatory processes (eigenvalues ± i ). A good criterion for the correctness of the calculation of the matrix exponent can be the relation:
connecting the eigenvalues of the matrix A and its matrix exponent.
Computational Experiment
To begin, we study the performance algorithms on random matrices of different sizes. As methods, we use the method of summing the Taylor series, the method of doubling the argument, and the expm function built into Octave . Initially, I also wanted to compare the correspondence of the eigenvalues, but I had to abandon this idea, since all three algorithms equally failed this check with the size of the matrix N ≳ 50. Perhaps the culprit was the function of determining the eigenvalues eig , which does not work accurately or the conditionality of the problem of determining the eigenvalues itself values for these matrices.
Based on the graph, the doubling method works approximately twice as long as the library function (it may be worth loosening the overestimated accuracy requirement), while direct summation even has a different asymptotic behavior ≈O (N 3.7 ), while the rest have the asymptotic behavior O (N 3 ).
Performance Testing Code
tries = 10;
N = 10;
while N < 1000
taylortime = 0;
dbltime = 0;
expmtime = 0;
for it = 1:tries
A = rand(N);
A = 0.5 * (A + A');
tic;
B2 = argdbl(1, A, 1e-20, 1e10);
dbltime = dbltime + toc;
tic;
B3 = expm(A);
expmtime = expmtime + toc;
tic;
B1 = taylorexp(1, A, 1e-20, 1e10);
taylortime = taylortime + toc;
end
taylortime = 1e3 * taylortime / tries;
dbltime = 1e3 * dbltime / tries;
expmtime = 1e3 * expmtime / tries;
printf('%d,%f,%f,%f\n', N, taylortime, dbltime, expmtime);
fflush(stdout);
N = round(N * 1.25);
end
Next, let’s check how the algorithm works with large eigenvalues. Consider the following system of ordinary differential equations
with the initial conditions:
Its peculiarity is that one of its eigenvalues is -1000 (a rapidly decaying solution), and the other two are ± i √2 (oscillatory solutions). If distortions are introduced into the imaginary eigenvalues, this will be clearly visible. Take a time step τ = 0.038, find the matrix exponent in
- The solution at the initial moment is known from the initial condition
- Knowing the solution u n at the moment t n , the solution at the moment t n + 1 = t n + τ is obtained from it by multiplying by the matrix exponent B:
- Repeat the second point until the end of the integration segment is reached.
Let's look at the obtained numerical trajectories (only the first component of the vector is displayed):
All the trajectories, except those obtained by direct summation of the Taylor series, visually coincide. Note that the graph does not go beyond the initial condition x 1 (0) = 1. In fact, the graph exponentially approaches the point y = 1, just the characteristic distance of the “rotation” of the graph (∼ 1/1000) is much less than the time step τ = 0.038.
ODE Decision Code
mu = 1000;
function [B] = trueexp(t, mu)
B = [
(exp(-mu*t) + cos(sqrt(2)*t))/2.,(-exp(-mu*t) + cos(sqrt(2)*t))/2.,sin(sqrt(2)*t)/sqrt(2);
(-exp(-mu*t) + cos(sqrt(2)*t))/2.,(exp(-mu*t) + cos(sqrt(2)*t))/2.,sin(sqrt(2)*t)/sqrt(2);
-(sin(sqrt(2)*t)/sqrt(2)),-(sin(sqrt(2)*t)/sqrt(2)),cos(sqrt(2)*t);
];
end
A = [-mu/2, mu/2, 1; mu/2, -mu/2, 1; -1, -1, 0];
t = 0:.038:100;
x0 = [1 0 1]';
B1 = trueexp(t(2), mu);
B2 = expm(t(2) * A);
B3 = taylorexp(t(2), A, 1e-20, 1e10);
B4 = argdbl(t(2), A, 1e-20, 1e10);
y1 = x0;
y2 = x0;
y3 = x0;
y4 = x0;
for i = 2:length(t)
y1 = B1 * y1;
y2 = B2 * y2;
y3 = B3 * y3;
y4 = B4 * y4;
printf('%f', t(i));
y = y1;
printf(' %e %e %e', y(1), y(2), y(3));
y = y2;
printf(' %e %e %e', y(1), y(2), y(3));
y = y3;
printf(' %e %e %e', y(1), y(2), y(3));
y = y4;
printf(' %e %e %e', y(1), y(2), y(3));
printf('\n');
end
Why such a strange time step
All norms of the matrix A have a value of the order of 1000. Accordingly, the norm of the matrix τA will be about 38. This value corresponds to the region (see the graph for the e -x function above), where rounding errors become significant when using the Taylor series “head-on” summation. If you take a step more, errors will grow catastrophically, the solution will quickly go beyond the limits of bit depth, if you take a step less, the effect will not be so noticeable.
We can say that the example is synthetic, and in practice it will not occur, but this is not so. There are many so-called rigid Cauchy problems , which are characterized by a strong scatter of eigenvalues (in fact, the rates of physical processes).
Further reading
The various methods of calculating the matrix exponent can be found in the article [English] [2]. A remarkable two-volume book has been written on the methods for solving ordinary differential equations and stiff problems [3,4]
List of sources used
- Fedorenko R.P. Introduction to computational physics. M .: Moscow Publishing House. physical and technical Institute, 1994 .-- 528s. § 17
- Cleve Moler and Charles Van Loan Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later // SIAM Rev. 45 (1), 3–49. (47 pages)
- Hyrer E., Nersett S., Wanner G. Solution of ordinary differential equations. Rigid tasks. M.: Mir,
1990 .-- 512 p. - Khairer E., Wanner G. Solution of ordinary differential equations. Rigid and differential algebraic problems. M .: Mir, 1999 .-- 685 p.
