Anatomy of melancholy

Knowledge is power.

       Francis Bacon.

... in much wisdom there is much sadness;
    and whoever multiplies knowledge, multiplies sorrow.

       Book of Ecclesiastes.

Games live their own lives. They arise from nowhere, develop, give rise to new games, are forgotten by everyone and, sometimes, come back from oblivion. There are many examples of games that have been defeated in this process of natural selection. These are the various variations of Shogi that have survived only thanks to the reverent attitude of the people of Japan to their cultural heritage. A game party like Taikyoku shogi could drag on for months (if not years). But these Heian- era chess dinosaursare not the most prominent representatives of the "fossil" world of board games.

I want to talk about a truly amazing game. The threats in it are not obvious, and the goals are not trivial. You can win in many ways, but playing is not at all easy. It cannot be attributed either to the family of Checkers or to the chess family. Its origin is foggy. For the average layman, this game is about as exciting as composing magic squares . It fully justifies one of its names - only philosophers can play it .

For the first time, Rithmomachia , also known as the “Battle of the Numbers” or “The Game of the Philosophers”, was described around 1030 by a monk named Asilo. Authorship, apparently unfounded, is attributedПлатону, а правила игры основаны на арифметической теории Боэция. Впоследствии, правила игры были незначительно изменены другим монахом, по имени Hermannus Contractus, добавившим примечания, посвященные теории музыки. Продолжительное время Ритмомахия использовалась в качестве учебного пособия, при обучении студентов математике. Интеллектуалы того времени играли в Ритмомахию для удовольствия (одно время она была даже более популярна чем Шахматы), Роберт Бёртон упоминал её в "Анатомии меланхолии", а Томас Мор считал эту игру хорошим досугом для обитателей своей "Утопии". Then, suddenly, it was over. The interests of mathematics and Rhythmachia diverged and the game was forgotten. Of course, this does not mean that we cannot remember it.

Rules of the game

Two players are playing Rhythm Machia on a rectangular 8x16 square board. The moves are made in turn. Each move moves one piece. As a result of the move, one or more pieces of the opponent can be taken (removed from the board). The following types of shapes are defined:

• A circle
• Triangle
• Square
• Pyramid

Ignoring the numerical marks on the figures (I will talk about them below), you can see that two types of moves are allowed. In the first case, the figure moves in a straight line and can be stopped by any other figure (its own or the enemy) that is in the way. Thus, the Circle moves (one cell diagonally), as well as the Triangle (strictly two cells along the orthogonal) and the Square (strictly three cells along the orthogonal). Another possibility is to “jump” the pieces onto the target square, similar to the move of the Knight in Chess. So the Triangle or the Square can walk. Any move should be performed only on an empty cell.

A unique figure is the Pyramid. Actually this is not a figure, but a set of figures. Each piece in the set (Circle, Triangle or Square) allows the Pyramid to perform the corresponding type of move. The figure above shows the possible moves of the Pyramid in the "maximum configuration". As you might guess, by the end of the game, “completeness” can be severely violated (by the way, the Pyramid from Rhythmachia is the only figure I know that can be “killed in parts”).

I will dwell on the methods of "killing". In Rhythmachia there are four of them:

• Capture by siege
• Capture by equality
• Capture by ambush
• Capture by eruption

The most radical is the siege of the figure. The figure will be removed if after the next move it is blocked in all diagonal or orthogonal directions. If the figure is located at the edge of the board or in the corner, you will have to block fewer directions. This is the simplest (but not the only) way to take the Pyramid all at once - as a whole. The siege is the only way that does not use the numerical values ​​of the figures.

Another way is to take a figure with a matching numerical value. If, after completing the move, on the field where the piece could move the next move (if this field was empty, of course), the opponent’s piece is located, with the same numerical value, it will be taken. It should be noted that this method of combat may be asymmetric. So (in the figure above), after White’s move, the Circle, with a numerical value of 16, can take a black Triangle with the same value, but the Triangle, in its turn, cannot do this, since it goes to other cells. At the same time, white and black triangles with numerical values ​​of 25 beat each other symmetrically (then which figure will be shot is determined by the order of the move).

An improved version of the previous is the following method. This time, "out of ambush", two figures are attacking. If the sum, difference, product or quotient of their numerical values ​​coincides with the numerical value on the opponent’s figure, the figure is removed. This is the most frequently used feature of the battle of figures in the game, but to see all such threats, in a more or less difficult position, can be quite difficult.

The latter method allows you to beat figures at a long distance. If the result of the work or the private numerical value of the figure and the distance to the opponent’s figure (orthogonal) coincides with the numerical value of the opponent’s figure, the figure is removed. Other figures located in the direction of the battle do not impede the threat. When calculating the distance, the start and end positions are taken into account. This is a symmetrical method of combat (since it does not depend on the rules for moving figures). The sequence of the move determines which of the figures will be taken.

It remains to talk about how these rules apply to the Pyramids. With this, everything is simple - in any calculation for taking figures, the Pyramid can act either as an independent figure (its numerical value coincides with the sum of the numerical values ​​of all its components), or as any of its parts. Similarly, the Pyramid can be taken as a whole (by its total value), or in parts (each of its components individually is vulnerable). Given the rules for moving the Pyramid, which I mentioned above, this makes the Pyramid the strongest (and most vulnerable) figure.



The initial arrangement of figures is associated with another important feature of the game. Although the set of figures is the same, the numerical values ​​vary. Also, the "complete set" of the pyramids is different (shown on the side of the board, for each of the players). This makes the game asymmetric. Tactics and strategies for the black player are not suitable for white (and vice versa). This makes the game more interesting.

Glorious victories

The rules described above are enough to start playing Rhythmachy, but if the goal of the game was to simply capture all the opponent’s pieces, the game would not be so interesting. Yes, you can win in this way, but this is not the only (and not the best) way to win! I really like games, the purpose of which is not a straightforward "killing" of enemy figures. So in Chess, to win, it is not at all necessary to “eat” all the pieces, it is enough to check the King! In some versions of Hasami Shogi , the goal of the game is even more unexpected (to win, you need to build a line of 5 of your chips “in a row”). Rhythmachy does not disappoint in this regard either. Here is a list of ways to win this game (in increasing order of their “fame”):

• De Corpore ("by body"): Get a given (or more) number of enemy pieces (usually 15)
• De Bonis (“by goods”): Take the opponent’s pieces with a given (or large) total value (usually 1315 for white and 984 for black)
• De Lite (“by lawsuit”): Take enemy figures with a given (or large) total value, provided that the number of digits on the captured figures does not exceed a given
• De Honore ("by honor"): Take enemy pieces with a given (or large) total value, provided that the number of captured pieces does not exceed a given
• De Honore Liteque (“by honor and lawsuit”): Take enemy figures with a given (or large) total value, provided that the number of captured figures does not exceed the specified and the number of digits on the captured figures does not exceed the specified
• Victoria Magna ("great victory"): Arrange three pieces (on enemy territory) in arithmetic progression
• Victoria Major (“greater victory”): Position four figures (on the territory of the enemy) so that they have two (but no more) groups of three figures placed in different types of progression ( arithmetic , geometric or harmonic )
• Victoria Excellentissima ("most excellent victory"): Position (on the territory of the enemy) four pieces so that there are all three types of progression

Here you can distinguish two fundamentally different types of goals of the game. Common Victories are associated with the capture of enemy figures (with the possible limitation of the number of captured figures, in order to protect against aggressive play). Proper Victories are considered a more worthy conclusion and are associated with the restoration of a certain “harmony” on the territory of the enemy (which does not exclude the possibility of the battle of enemy figures).



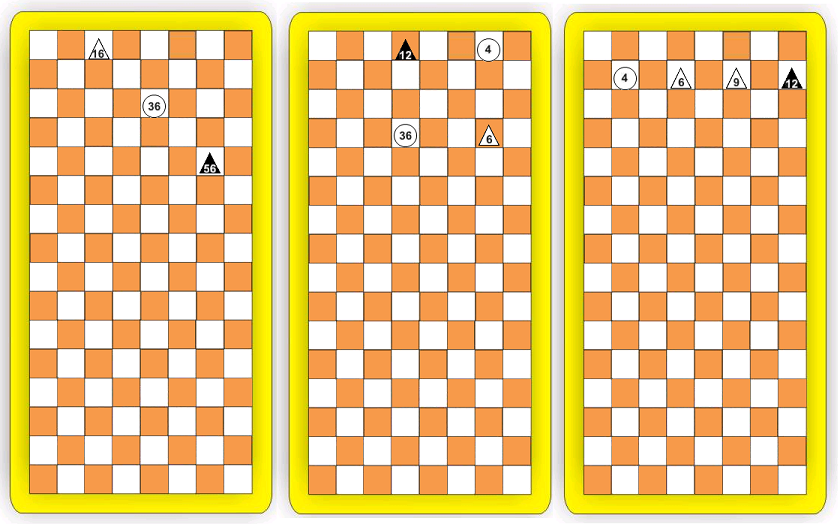
The examples above illustrate that enemy figures can (and should) be involved. In the first case, an arithmetic progression is constructed (16, 36, 56). The second example combines geometric (4, 12, 36) and harmonic (4, 6, 12) progressions. In the third case, all three types of progression are present (you yourself can find them). In case there are difficulties with verbal counting, tables of all possible solutions in Rhythmachy have been built (however, Rhythmachy is unlikely to be of interest to people with problems with verbal counting).

Possible options

During its heyday, Rhythmachy has already undergone many changes. Subsequent renovations did not improve the situation. There are many differences in the description of the rules of this game. Some sources give alternative options for the initial arrangement of pieces (I even came across an option that describes the game on an 8 x 14 board):



There are options with simplified rules for moving pieces. According to these rules, figures move in a straight line (orthogonal and diagonal) by a given number of cells. Any figure, in the way of movement, stops moving. There are no jumps, like a Knight's move in Chess. The pyramid, as usual, combines the moves of the figures present in its set.



In addition, there is an option with the usual rules for the movement of figures, in which a special Pyramid move is added to 3 cells diagonally. Such a move is possible provided that not one of the figures originally included in the Pyramid is taken. With the safety of the initial set of figures of the Pyramid, another option is associated. It is allowed to use the total value of the Pyramid, only on condition that none of its figures has not yet been "eaten". There are simpler options in which the Pyramid is completely removed if any of its components is attacked.

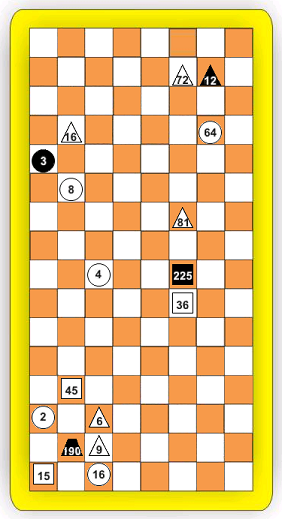
Some of the options are related to changes in the rules for taking figures. So, in one of the options for taking a piece " by Siege" (осада), необходимо блокировать все направления её «естественного» перемещения. При этом, не обязательно располагать свои фигуры вплотную к блокируемой (примеры ниже иллюстрируют концепцию). Это довольно интересное правило.



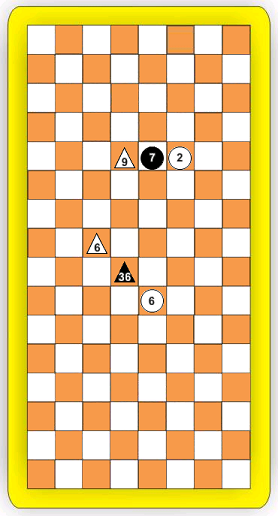
Есть вариант, в котором взятие "by Ambush" (засада) осуществляется подобно играм «зажимного» типа (при этом, правила перемещения фигур игнорируются):



Имеется большое количество расхождений в определениях "Glorious Victories". Часто, в условия таких побед, включается предварительное уничтожение Пирамиды противника. Также, существует условие завершения игры, ограничивающееся взятием Пирамиды. Вариантов этой игры много. Ознакомление с нюансами правил, перед началом игры, в любом случае, будет совсем не лишним.

Details for the curious

The implementation of the game naturally divided into several stages. The easiest way was to implement moving shapes. This is where I started. Here's what the Squares move looks like:


Some difficulty arose with the Pyramids, since their set of moves is determined by what pieces are included in them at the moment. I had to describe all possible moves for them, and when making a move, check for the presence of the corresponding figure in the set:


The implementation of the battle of figures turned into a real "race for survival." It was required to implement four completely different (and very non-trivial) methods of capture. At the same time, I wanted to limit the number of field views in order to minimize the overhead of calculations (the move is calculated disgracefully long already). As a result, I settled on the idea of ​​pre-filling several arrays, with the following checks of the conditions of the battle of figures:


The capture of figures in the Pyramid, as well as the movement, had to be handled in a special way:


Already in the process of debugging, I realized that all checks are performed at the time before the move. I had to write a small function that simulates the movement of a piece (this is not a very complete recalculation of the position on the board, but I managed to get by with a little blood):


Against the background of all these horrors, checking the conditions for ending the game seemed a trivial task. There was some Axiom magic, but there is nothing that I’m afraid to show my parents:


From this moment, the program could already play (though it did it rather passively). The fact is that, in the absence of an evaluation function (and a custom implementation of AI), Axiom tries to perform a complete exhaustive search, to the terminal position. It is clear that the end of the game is far beyond the horizon of the possible depth of search, as a result of which the moves found do not differ in particular meaningfulness. In general, it remains to add AI teeth:


Here we used the very convenient material-balance function (provided by Axiom), which uses the weight values ​​given to the figures (the same values ​​were used to implement the Rhythmachy rules):


This implementation lacks a lot (for example, checking for game completion by Glorious Victories ). I will try to add the missing functionality in the future. The current version of the source code can always be found here .

What is the result?

Rhythmachy interested me, first of all, with its complexity. Of course, there were no thoughts to implement it on ZRF . I had to master Axiom , for this! Currently, there is a simplified implementation that does not support Glorious Victories . Also, there is no firm belief that I found all the errors in the code (1000 lines in ForthScript - this is serious). This is a beta version, but overall it works:



You may notice that the game ends very quickly. It really is. In case both players play aggressively, according to the terms of Common Victories (and without limiting the number of pieces taken), the average duration of a game is ~ 10 moves. At the same time, the first player has a serious advantage:

Cumulative results following game 13 of 100:
Player 1 "Eval", wins = 13.
Player 2 "Eval", wins = 0.
Draws = 0

It's funny that if only one of the players is aggressive, the game drags on to more than 300 moves (an aggressive player almost always wins).

Cumulative results following game 22 of 100:
Player 1 "Rithmomachy", wins = 1.
Player 2 "Eval", wins = 21.
Draws = 0

It's hard for a person with a computer to play. Even with the highlight of the figures under battle, it can be difficult to figure out which particular piece to make a move in order to take (although it is also advisable not to substitute your own figures). Nowadays, this game is unlikely to be popular, but one cannot be taken away from it. She is great at developing her oral counting skills.