Factorization and natural number classes
Accept the abbreviations: natural series of numbers (NRF); the problem of factorization of large numbers (ZFBCH).
Manipulation with natural numbers is possible both directly with values and with characteristics - properties of numbers. The convenience of such manipulation is largely determined by the model of the number. It is desirable to have a limited variety of models, and structural construction simple. Descriptions of the properties of models of natural numbers (however, and any other numbers) are desirable to have in quantitative terms, in a formalized form. The dependence of the values of property indicators on the bit depth of numbers must be eliminated, or properties selected free of such dependencies. Any classification basically has properties - it is an element of formalization. The main issue in the work is the factorization of numbers - in connection with which we formulate below a version of the theorem of factorization of a natural number.
The theorem states that the difficulties of factorization do not arise for all numbers; therefore, it is necessary to subject the complicated factorization procedure not to all the numbers of NRFs, but only to some (smaller) part of them. The text of the theorem does not say how to formalize this smaller part and make it convenient for further processing. But the discussion will focus on the formation of a representation of numbers of such a smaller set that is convenient for processing.
Factorization theorem for natural numbers
An arbitrary composite natural number N by successively performing some elementary transformations on it can be represented by a product of the form
N = 2 t 2 ∙ 3 t 3 ∙ 5 t 5 ∙ (p k+ 30 ∙ t), where 0 ≤ t i , i = 2,3,5, t is positive integer, p k > 5 is prime.
Theorem
1. If N is a composite even natural number, then it can be represented in the form N = 2 t 2 ∙ n 2 ,
where n 2 ≡ 1 (mod 2) is a composite odd number, t 2 = 1 (1) ..., and 2 ∤ n 2 ;
2. If N = n 2 is a composite odd number ending with the number 5, then it can be represented as N = 5 t 5 ∙ n 5 , where n 5 is a composite odd number, t 5 = 1 (1) ...; and 5 ∤ n 5 ;
3. If N = n 5Is a composite odd number that does not end with the number 5, and its convolution s (N) (the sum of the digits) is a multiple of 3, then it can be represented as N = 3 t 3 ∙ n 3 , where n 3 is a composite odd number,
t 3 = 1 (1) ...; and 3 ∤ n 3 ;
4. If N = n 3 is a composite odd number, with the last digit ( flexion ) ф ϵ {1, 3, 7, 9}, then it has the form N = (p k + 30 ∙ t), where t = 1 ( 1) ... is a positive integer, and p k ϵ {7,11,13,17,19,23,29,31}, and factorization can be performed, for example, using the notion of limit contour and φ-invariantodd number or one of the existing known methods.
Instead of proof. Further, the text of the work, including Table 3, is essentially a proof of the first part of the theorem (on the representation of a number in the form of a model N = 30 ∙ t + p k) In the course of exposition, complete and truncated models of NRF appear, flat and three-dimensional. The set of all natural numbers is divided into two subsets. The first one is intuitively perceived as containing more natural numbers that are factorized by elementary means (the simplest signs of divisibility into prime numbers 2, 3, 5 are used). The second subset is the smaller one, which contains all the odd primes (except for 3 and 5), and the factorization of which is especially for large numbers an insurmountable problem of the present. The last published factorized number is described in 232 decimal digits.
The well-known analytical model of NRF in the form of a list of 30k, 30k ± 1, 30k ± 3, ..., 30k ± 15,
k = 1 (1) ∞, of the relations allows us to understand how we can describe those of the numbers that should be contained in each of the indicated subsets, i.e., essentially carry out such a partition of the LDP.
The multiplicative representation of 30 has the form 30 = 2 ∙ 3 ∙ 5. Natural numbers N, comparable with zero modulo divisors of 30,N ≡ 0 (mod2), N ≡ 0 (mod3), N ≡ 0 (mod5) are all even numbers, numbers divisible by three without remainder, and odd numbers ending with the number 5.
It turns out that a set of natural numbers with a violation of such properties splits into equivalence classes with other simple, clearly distinguishable attributes. Thus, the task in the work is to divide the NRF into two subsets, and obtain a description of the smaller one in a simple and convenient form for further processing of numbers.
Classes of natural numbers. We put as the basis of the classification in question two very easily defined indicators of the properties (s, f) of numbers. The first indicator is denoted by the symbol s,
1 ≤ s ≤ 9, is called the convolution (this is the sum of the digits of the number reduced to one digit) of the number, it characterizes the property of divisibility of the number by three, and the second indicator is denoted by the symbol ф,
0 ≤ ф ≤ 9, inflection(end, last digit) of a number, characterizes the property of a finite number to have the last digit.
Example 1 . N = 4757, s (N) = ((4 + 7 + 5 + 7 = 23) → (2 + 3)) = 5; f (N) ≡ N (mod10) = 7.
A pair of properties of numbers characterized by exponents (s, f) breaks up the LDP into non-intersecting classes (equivalences) that have the same values for a pair of exponents. A characteristic of the class of numbers to which the number N = 4757 belongs is a pair with the value (s, φ) = (5, 7).
The number T (s, f) of classes of numbers distinguishable by such a characteristic is determined by the product of the ranges of variation in the values of each indicator of the two properties of the number
T (S, Ф) = S × Ф = 9 × 10 = 90.
The volume of each class includes an infinite number of natural numbers, among which there is the smallest number in the class. We place the smallest representatives of all classes on the left side of table 1, and on the right we continue by filling in (according to the sample on the left) the cells of the tables in a row with the following natural numbers.
Table 1 - Classes T (s, f) of numbers with a period of 90. The flat model of the NRF

An analysis of the contents of the table (the set of T-90 numbers) shows that on the left side of the 10 × 9 table all numbers are the smallest in their class and have different characteristic values (s, f). The right side of the 10 × 9 table is similarly to the left side filled with representatives of different classes with the same characteristic (s, f), but with the next value (period) of the element increased by 90 units. Such tables can be continued indefinitely and shifted to the left with the overlay on the 1st (left) table. As a result, we obtain a three-dimensional parallelepiped, in which all the numbers that form the class of natural numbers with a fixed value of the pair (s, φ) are written over each cell of the lower table.
3D Model
In essence, we have obtained yet another volumetric model of NRF. Its advantages are manifested in the ability to significantly reduce NRF without losing important positions, for example, positions containing prime numbers. We show how this can be done.
First, cross out the lines of table 1 that contain even and odd numbers ending in five, and secondly, delete the classes of numbers that are multiples of three. Table cells of such classes belong to diagonals parallel to the side diagonal of the table. In table 1, the deleted cells (classes) are highlighted with a fill.
The unfilled cell-classes T (s, f) are preserved, the number of which is 24 (the remaining ones after deleting the number will be called the T-24 set), they correspond to the cells of the table without filling. Possible inflections in the remaining classes will be only f = 1,3,7,9 and with each inflection there are 6 convolution values, i.e., 24 classes. It is obvious that primes can appear within only these classes. Indeed, in the left table of the 24 smallest representatives of all classes, 22 are primes. Only two cells (out of 24) are filled with compound numbers 7 × 7 = 49 and7 × 11 = 77 , obtained by multiplying the smallest remaining prime number 7 by itself and by the next prime number 11.
An algebraic group of residues of class generators
We will continue the reform of the NRF, we will return to the number 30 = 2 ∙ 3 ∙ 5. Recall that the eight primes p (i) = {7,11,13,17,19,23,29,31} forms the multiplicative group E (Euler group) of eighth-order residues modulo this. The unit element is identified with a prime number 31, p (i) ≡ 31 (mod30) = 1. By the Lagrange theorem (on the orders of groups), the group может can have proper subgroups of the 2nd and 4th orders. Elements of the 8th order group (11,19 and 29) are of the 2nd order; (7,13, 17, 23) 4th order and unit. There are three subgroups of the 4th order: one (1,11,19,29) - includes only involutions, and two cyclic subgroups:
7 × 7 ≡ 49 (mod30) = 19; 19 × 7 ≡ 133 (mod30) = 13; 13 × 7 ≡ 91 (mod30) = 1;
11 × 19 ≡ 209 (mod30) = 29; 11 × 29 ≡ 319 (mod30) = 19; 19 × 29 ≡ 551 (mod30) = 1;
17 × 17 ≡ 289 (mod30) = 19; 19 × 17 ≡ 323 (mod30) = 23; 23 × 17≡ 391 (mod30) = 1;
Surprisingly, all the numbers in the 24 classes | T (S, Φ) | = 3 × 8 are transformed into a family of classes consisting of only 8 classes generated by each representative of the set p (i). In the new classes of numbers - elements follow with a period of not 90, but three times smaller, only 30.
Table 2 - Multiplicative subgroups of the residue group (p k ) by mod30
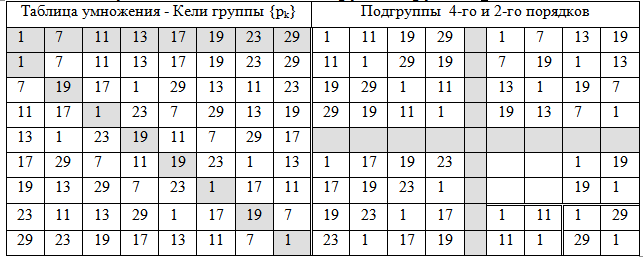
Classes are formed taking into account the inflection and convolution of numbers of three pairs (2, 1), (5.1), (8.1); (4.1), (7.1), (1.1); (2.3), (5.3), (8.3); (4.3), (7.3), (1.3); (7.7), (1.7), (4.7); (8.7), (2.7), (5.7); (7.9), (1.9), (4.9); (8.9), (2.9), (5.9);
Below in table 3 we give the initial fragments of these 8 classes. Any odd number N> 31 not multiple of 3 or 5 has the form N = p (i) + 30t and falls into one of the 8 classes presented in Table 3. We call the set of numbers from such a table the set T - 8.
Table 3 - Classes of numbers with a period of 30. Prime numbers {p k } are highlighted by filling.

Even a superficial analysis of the table allows us to draw some conclusions regarding simplicity, complexity and the possibility of factorization of numbers:
- all degrees of all class generators, i.e. prime numbers are compound;
- rows with a number multiple to the generator in the cell column of this generator contain composite numbers whose divisor is the generator;
– числа, принадлежащие области запрета простых чисел в спирали Улама, – составные, примеры таких чисел в первой тысяче:143,161,203,217,323,451, 517,539,473, 611,637 и др.
– числа, допускающие разложение в сумму- разность и вынесение за скобку общего множителя, например, 217 =210+7 =7(30 +1) =7×31; 1397 = 1270 +127 = 127(10 +1) = 127×11.
Таким образом, элементарными средствами и операциями удается селектировать множество Т-8 нечетных чисел НРЧ, которые должны и могут служить объектом последующего исследования в интересах решения как теоретических, так и прикладных практических задач. К числу таких задач в области криптологии и информационной безопасности следует отнести следующие: ЗФБЧ, задачу установления простоты числа, задачу дискретного логарифма в конечных полях и группах точек эллиптических кривых.
The set of T-8 numbers is organized in a special way (consists of 8 classes), the smallest representatives of the classes form a group of residues modulo 30 (φ (30) = 8). This property provides the determination of the column number of the result of the product of a pair of numbers whose column numbers are known. The Keli group table provides a solution to this problem.
The purpose of the examples is to show what information about the relationships between the values of numbers, row numbers and column numbers is contained in the set T-8.
One of the possible methods of factoring the numbers of the set T-8 using table 3.
Example 2 . Let an odd positive integer (snc) be given
N = 1727. It is required to factorize it. Find the position of this number in the set T-8: row number N / 30 = 57 (the integer part of the fraction is taken), column number (name) N - 30 ∙ 57 = 17. In this same column we specify the product 7 ∙ 11 = 77, number whose line is 2.
Try to save each of the dividers. We save d1 = 7, another divisor N takes the form
d2 = 11 + 30 ∙ t, where t is determined through the difference in line numbers and the stored divisor
t = (57 - 2) / 7 = 7.85. We obtained a fractional value, from which it follows that 7 is not a divisor of a given number 1727. In fact, you can immediately find out by trial division whether di is a divisor of a given number.
We save d2 = 11, another divisor takes the form d1 = 7 + 30 ∙ t, where t is determined through the difference in line numbers and the stored divisor t = (57 - 2) / 11 = 5. Then d1 = 7 + 30 ∙ t = 157.
Indeed, 1727/157 = 11.
Example 3. Let an odd positive integer (snc) be given
N = 4294967297, outside the table. Required to factorize it. We will find, as before, the position of this number in the set T-8:
row number N / 30 = 143165576,
column number N - 30 ∙ 143165576 = 17.
In the same column we specify the product 7 ∙ 641 = 4487, whose row number is 149.
We try save each of the dividers. We save d1 = 641, another divider takes the form
7 + 30 ∙ t, where t is determined through the line difference and the stored divisor
t = (143165576 - 149) / 641 = 143165427/641 = 223347.
The value t = 223347 is an integer, therefore, 641 is the divisor of the original number N.
Indeed, N / d1 = 4294967297: 641 = 6700417 is a prime number (another divisor).
Manipulation with natural numbers is possible both directly with values and with characteristics - properties of numbers. The convenience of such manipulation is largely determined by the model of the number. It is desirable to have a limited variety of models, and structural construction simple. Descriptions of the properties of models of natural numbers (however, and any other numbers) are desirable to have in quantitative terms, in a formalized form. The dependence of the values of property indicators on the bit depth of numbers must be eliminated, or properties selected free of such dependencies. Any classification basically has properties - it is an element of formalization. The main issue in the work is the factorization of numbers - in connection with which we formulate below a version of the theorem of factorization of a natural number.
The theorem states that the difficulties of factorization do not arise for all numbers; therefore, it is necessary to subject the complicated factorization procedure not to all the numbers of NRFs, but only to some (smaller) part of them. The text of the theorem does not say how to formalize this smaller part and make it convenient for further processing. But the discussion will focus on the formation of a representation of numbers of such a smaller set that is convenient for processing.
Factorization theorem for natural numbers
An arbitrary composite natural number N by successively performing some elementary transformations on it can be represented by a product of the form
N = 2 t 2 ∙ 3 t 3 ∙ 5 t 5 ∙ (p k+ 30 ∙ t), where 0 ≤ t i , i = 2,3,5, t is positive integer, p k > 5 is prime.
Theorem
1. If N is a composite even natural number, then it can be represented in the form N = 2 t 2 ∙ n 2 ,
where n 2 ≡ 1 (mod 2) is a composite odd number, t 2 = 1 (1) ..., and 2 ∤ n 2 ;
2. If N = n 2 is a composite odd number ending with the number 5, then it can be represented as N = 5 t 5 ∙ n 5 , where n 5 is a composite odd number, t 5 = 1 (1) ...; and 5 ∤ n 5 ;
3. If N = n 5Is a composite odd number that does not end with the number 5, and its convolution s (N) (the sum of the digits) is a multiple of 3, then it can be represented as N = 3 t 3 ∙ n 3 , where n 3 is a composite odd number,
t 3 = 1 (1) ...; and 3 ∤ n 3 ;
4. If N = n 3 is a composite odd number, with the last digit ( flexion ) ф ϵ {1, 3, 7, 9}, then it has the form N = (p k + 30 ∙ t), where t = 1 ( 1) ... is a positive integer, and p k ϵ {7,11,13,17,19,23,29,31}, and factorization can be performed, for example, using the notion of limit contour and φ-invariantodd number or one of the existing known methods.
Instead of proof. Further, the text of the work, including Table 3, is essentially a proof of the first part of the theorem (on the representation of a number in the form of a model N = 30 ∙ t + p k) In the course of exposition, complete and truncated models of NRF appear, flat and three-dimensional. The set of all natural numbers is divided into two subsets. The first one is intuitively perceived as containing more natural numbers that are factorized by elementary means (the simplest signs of divisibility into prime numbers 2, 3, 5 are used). The second subset is the smaller one, which contains all the odd primes (except for 3 and 5), and the factorization of which is especially for large numbers an insurmountable problem of the present. The last published factorized number is described in 232 decimal digits.
The well-known analytical model of NRF in the form of a list of 30k, 30k ± 1, 30k ± 3, ..., 30k ± 15,
k = 1 (1) ∞, of the relations allows us to understand how we can describe those of the numbers that should be contained in each of the indicated subsets, i.e., essentially carry out such a partition of the LDP.
The multiplicative representation of 30 has the form 30 = 2 ∙ 3 ∙ 5. Natural numbers N, comparable with zero modulo divisors of 30,
It turns out that a set of natural numbers with a violation of such properties splits into equivalence classes with other simple, clearly distinguishable attributes. Thus, the task in the work is to divide the NRF into two subsets, and obtain a description of the smaller one in a simple and convenient form for further processing of numbers.
Classes of natural numbers. We put as the basis of the classification in question two very easily defined indicators of the properties (s, f) of numbers. The first indicator is denoted by the symbol s,
1 ≤ s ≤ 9, is called the convolution (this is the sum of the digits of the number reduced to one digit) of the number, it characterizes the property of divisibility of the number by three, and the second indicator is denoted by the symbol ф,
0 ≤ ф ≤ 9, inflection(end, last digit) of a number, characterizes the property of a finite number to have the last digit.
Example 1 . N = 4757, s (N) = ((4 + 7 + 5 + 7 = 23) → (2 + 3)) = 5; f (N) ≡ N (mod10) = 7.
A pair of properties of numbers characterized by exponents (s, f) breaks up the LDP into non-intersecting classes (equivalences) that have the same values for a pair of exponents. A characteristic of the class of numbers to which the number N = 4757 belongs is a pair with the value (s, φ) = (5, 7).
The number T (s, f) of classes of numbers distinguishable by such a characteristic is determined by the product of the ranges of variation in the values of each indicator of the two properties of the number
T (S, Ф) = S × Ф = 9 × 10 = 90.
The volume of each class includes an infinite number of natural numbers, among which there is the smallest number in the class. We place the smallest representatives of all classes on the left side of table 1, and on the right we continue by filling in (according to the sample on the left) the cells of the tables in a row with the following natural numbers.
Table 1 - Classes T (s, f) of numbers with a period of 90. The flat model of the NRF

An analysis of the contents of the table (the set of T-90 numbers) shows that on the left side of the 10 × 9 table all numbers are the smallest in their class and have different characteristic values (s, f). The right side of the 10 × 9 table is similarly to the left side filled with representatives of different classes with the same characteristic (s, f), but with the next value (period) of the element increased by 90 units. Such tables can be continued indefinitely and shifted to the left with the overlay on the 1st (left) table. As a result, we obtain a three-dimensional parallelepiped, in which all the numbers that form the class of natural numbers with a fixed value of the pair (s, φ) are written over each cell of the lower table.
3D Model
In essence, we have obtained yet another volumetric model of NRF. Its advantages are manifested in the ability to significantly reduce NRF without losing important positions, for example, positions containing prime numbers. We show how this can be done.
First, cross out the lines of table 1 that contain even and odd numbers ending in five, and secondly, delete the classes of numbers that are multiples of three. Table cells of such classes belong to diagonals parallel to the side diagonal of the table. In table 1, the deleted cells (classes) are highlighted with a fill.
The unfilled cell-classes T (s, f) are preserved, the number of which is 24 (the remaining ones after deleting the number will be called the T-24 set), they correspond to the cells of the table without filling. Possible inflections in the remaining classes will be only f = 1,3,7,9 and with each inflection there are 6 convolution values, i.e., 24 classes. It is obvious that primes can appear within only these classes. Indeed, in the left table of the 24 smallest representatives of all classes, 22 are primes. Only two cells (out of 24) are filled with compound numbers 7 × 7 = 49 and
An algebraic group of residues of class generators
We will continue the reform of the NRF, we will return to the number 30 = 2 ∙ 3 ∙ 5. Recall that the eight primes p (i) = {7,11,13,17,19,23,29,31} forms the multiplicative group E (Euler group) of eighth-order residues modulo this. The unit element is identified with a prime number 31, p (i) ≡ 31 (mod30) = 1. By the Lagrange theorem (on the orders of groups), the group может can have proper subgroups of the 2nd and 4th orders. Elements of the 8th order group (11,19 and 29) are of the 2nd order; (7,13, 17, 23) 4th order and unit. There are three subgroups of the 4th order: one (1,11,19,29) - includes only involutions, and two cyclic subgroups:
7 × 7 ≡ 49 (mod30) = 19; 19 × 7 ≡ 133 (mod30) = 13; 13 × 7 ≡ 91 (mod30) = 1;
11 × 19 ≡ 209 (mod30) = 29; 11 × 29 ≡ 319 (mod30) = 19; 19 × 29 ≡ 551 (mod30) = 1;
17 × 17 ≡ 289 (mod30) = 19; 19 × 17 ≡ 323 (mod30) = 23; 23 × 17≡ 391 (mod30) = 1;
Surprisingly, all the numbers in the 24 classes | T (S, Φ) | = 3 × 8 are transformed into a family of classes consisting of only 8 classes generated by each representative of the set p (i). In the new classes of numbers - elements follow with a period of not 90, but three times smaller, only 30.
Table 2 - Multiplicative subgroups of the residue group (p k ) by mod30

Classes are formed taking into account the inflection and convolution of numbers of three pairs (2, 1), (5.1), (8.1); (4.1), (7.1), (1.1); (2.3), (5.3), (8.3); (4.3), (7.3), (1.3); (7.7), (1.7), (4.7); (8.7), (2.7), (5.7); (7.9), (1.9), (4.9); (8.9), (2.9), (5.9);
Below in table 3 we give the initial fragments of these 8 classes. Any odd number N> 31 not multiple of 3 or 5 has the form N = p (i) + 30t and falls into one of the 8 classes presented in Table 3. We call the set of numbers from such a table the set T - 8.
Table 3 - Classes of numbers with a period of 30. Prime numbers {p k } are highlighted by filling.

Even a superficial analysis of the table allows us to draw some conclusions regarding simplicity, complexity and the possibility of factorization of numbers:
- all degrees of all class generators, i.e. prime numbers are compound;
- rows with a number multiple to the generator in the cell column of this generator contain composite numbers whose divisor is the generator;
– числа, принадлежащие области запрета простых чисел в спирали Улама, – составные, примеры таких чисел в первой тысяче:143,161,203,217,323,451, 517,539,473, 611,637 и др.
– числа, допускающие разложение в сумму- разность и вынесение за скобку общего множителя, например, 217 =210+7 =7(30 +1) =7×31; 1397 = 1270 +127 = 127(10 +1) = 127×11.
Таким образом, элементарными средствами и операциями удается селектировать множество Т-8 нечетных чисел НРЧ, которые должны и могут служить объектом последующего исследования в интересах решения как теоретических, так и прикладных практических задач. К числу таких задач в области криптологии и информационной безопасности следует отнести следующие: ЗФБЧ, задачу установления простоты числа, задачу дискретного логарифма в конечных полях и группах точек эллиптических кривых.
The set of T-8 numbers is organized in a special way (consists of 8 classes), the smallest representatives of the classes form a group of residues modulo 30 (φ (30) = 8). This property provides the determination of the column number of the result of the product of a pair of numbers whose column numbers are known. The Keli group table provides a solution to this problem.
The purpose of the examples is to show what information about the relationships between the values of numbers, row numbers and column numbers is contained in the set T-8.
One of the possible methods of factoring the numbers of the set T-8 using table 3.
Example 2 . Let an odd positive integer (snc) be given
N = 1727. It is required to factorize it. Find the position of this number in the set T-8: row number N / 30 = 57 (the integer part of the fraction is taken), column number (name) N - 30 ∙ 57 = 17. In this same column we specify the product 7 ∙ 11 = 77, number whose line is 2.
Try to save each of the dividers. We save d1 = 7, another divisor N takes the form
d2 = 11 + 30 ∙ t, where t is determined through the difference in line numbers and the stored divisor
t = (57 - 2) / 7 = 7.85. We obtained a fractional value, from which it follows that 7 is not a divisor of a given number 1727. In fact, you can immediately find out by trial division whether di is a divisor of a given number.
We save d2 = 11, another divisor takes the form d1 = 7 + 30 ∙ t, where t is determined through the difference in line numbers and the stored divisor t = (57 - 2) / 11 = 5. Then d1 = 7 + 30 ∙ t = 157.
Indeed, 1727/157 = 11.
Example 3. Let an odd positive integer (snc) be given
N = 4294967297, outside the table. Required to factorize it. We will find, as before, the position of this number in the set T-8:
row number N / 30 = 143165576,
column number N - 30 ∙ 143165576 = 17.
In the same column we specify the product 7 ∙ 641 = 4487, whose row number is 149.
We try save each of the dividers. We save d1 = 641, another divider takes the form
7 + 30 ∙ t, where t is determined through the line difference and the stored divisor
t = (143165576 - 149) / 641 = 143165427/641 = 223347.
The value t = 223347 is an integer, therefore, 641 is the divisor of the original number N.
Indeed, N / d1 = 4294967297: 641 = 6700417 is a prime number (another divisor).
