About Bayes formula, forecasts and confidence intervals
There are a lot of articles on Habré on this topic, but they do not consider practical problems. I will try to correct this annoying misunderstanding. Bayes formula is used to filter spam, in recommendation services and in ratings. Without it, a significant number of fuzzy search algorithms would be impossible. In addition, this formula was the cause of holivar among mathematicians.
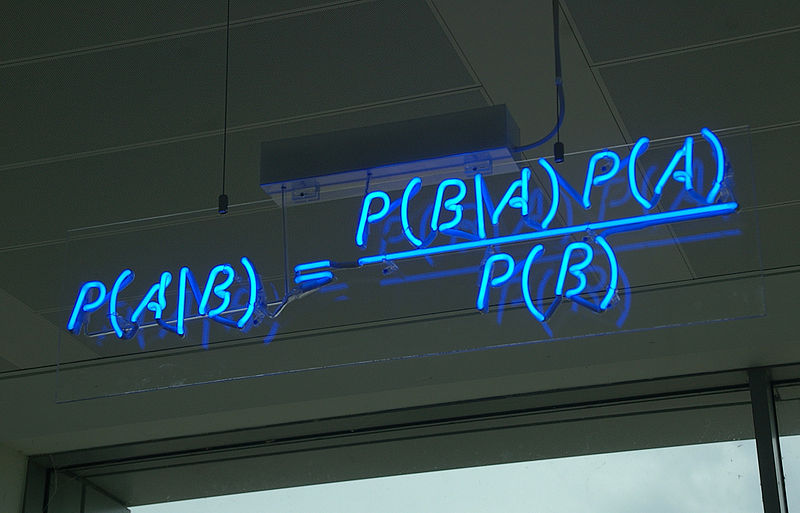
Let's start from afar. If the onset of one event increases or decreases the likelihood of another, then such events are called dependent. Terver does not study causation. Therefore, dependent events are not necessarily consequences of each other, the connection may not be obvious. For example, “a person has blue eyes” and “a person knows Arabic” are dependent events, since Arabs have extremely rare blue eyes.
Now we should introduce the notation.
Let's think about what is the probability of the occurrence of two events at the same time. P (AB). The probability of the onset of the first event multiplied by the probability of the onset of the second event, in the event of the onset of the first. P (AB) = P (A) P (B | A). Now, if we recall that P (AB) = P (BA). We obtain P (A) P (B | A) = P (B) P (A | B). Move P (B) to the left and get the Bayes formula:
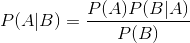
Everything is so simple that a simple priest deduced this formula 300 years ago. But this does not reduce the practical value of this theorem. It allows you to solve the "inverse problem": according to tests to assess the situation.
The direct problem can be described as follows: for the reason, find the probability of one of the consequences. For example, an absolutely symmetric coin is given (the probability of falling an eagle, like tails, is 1/2). We need to calculate the probability that if we flip a coin twice, an eagle will fall both times. Obviously, it is 1/2 * 1/2 = 1/4.
But the problem is that we only know the probability of this or that event in a minority of cases, almost all of which are artificial, for example, gambling. Moreover, there is nothing absolute in nature, the probability of an eagle falling out of a real coin is 1/2 only approximately. We can say that the direct problem studies some spherical horses in a vacuum.
In practice, the inverse problem is more important: to assess the situation according to the test data. But the problem of the inverse problem is that its solution is more complicated. Mainly due to the fact that our solution will not be the point P = C, but some function P = f (x).
For example, we have a coin, we need to evaluate the probability of tails by experiments. If we tossed a coin 1 time and an eagle fell, this does not mean that eagles always drop. If 2 times tossed and received 2 eagles, then again this does not mean that only eagles fall. To get the exact probability of the tails falling, we must toss a coin an infinite number of times. In practice, this is not possible and we always calculate the probability of an event with some accuracy.
We are forced to use some function. Usually it is customary to denote it as P (p = x | s tails, f eagles) and call it the probability density. This is read as the probability that the probability of an eagle falling is x if, according to the experiment, s tails and f eagles fell out. Sounds complicated sounds due to taftology. It is simpler to consider p some property of a coin, and not probability. And read: so the probability is that p = x ...
Looking ahead, I’ll say that if we throw in the first coin 1000 times and get 500 eagles, and the second 10,000 and get 5000 eagles, then the probability densities will look like this:

Due to the fact that we do not have a point, but a curve, we are forced to use confidence intervals. For example, if they say the 80% confidence interval for p is 45% to 55%, then this means that with 80% probability p will be between 45% and 55%.
For simplicity, we consider a binomial distribution. This is the distribution of the number of “successes” in a sequence of a number of independent random experiments, such that the probability of “success” in each of them is constant. It is almost always observed when we have a test sequence with two possible outcomes. For example, when we toss a coin several times, or evaluate the CTR of a banner, or the conversion on a site.
For example, we assume that we need to evaluate the probability of the tails falling out of a coin. We flipped a coin a number of times and got f eagles and s tails. We denote this event as [s, f] and substitute it into the Bayes formula instead of B. The event when p is equal to a certain number will be denoted as p = x and substitute instead of event A.
P ([s, d] | p = x), The probability of getting [s, d] if p = x, provided that p = x we know P ([s, f] | p = x) = K ( f, s) * x ^ s (1-x) ^ f. Where K (f, s) is a binomial coefficient. We get:

We do not know P ([s, f]). And the binomial coefficient is difficult to calculate: there are factorials. But these problems can be solved: the total probability of all possible x should be equal to 1.
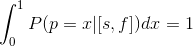
Using simple transformations, we get the formula: This is
programmed simply, just 10 lines:
However, P (p = x) remains unknown. It expresses how likely it is that p = x if we do not have experimental data. This function is called a priori. Because of it, there was a holivar in probability theory. We cannot strictly mathematically calculate a priori, only set subjectively. And without a priori, we cannot solve the inverse problem.
Proponents of the classical interpretation (frequency approach, emergency), believe that all possible p are equally probable before the experiment. Those. Before the experiment, you need to “forget” the data that we know before. Their opponents, supporters of the Bayesian approach (BP), believe that you need to set some a priori based on our knowledge before the experiment. This is a fundamental difference, even the definition of the concept of probability for these groups is different.
By the way, the creator of this formula, Thomas Bayes, died 200 years earlier than the holivar and has only indirect relation to this dispute. Bayes formula is part of both competing theories.
The frequency approach (PE) is better suited for science where it is necessary to objectively prove a hypothesis. For example, the fact that mortality from a drug is less than a certain threshold. If you need, taking into account all the available information, make a decision, then it is better to use a PSU.
PE is not suitable for forecasting. By the way, confidence interval formulas, consider confidence interval by emergency. BP supporters usually use the Beta distribution as a priori for the binomial distribution, with a = 1 and b = 1 it degenerates into a continuous distribution, which their opponents use. As a result, the formula takes the form:
=x^{s+\alpha%20-1}%20(1-x)^{f+\beta%20-1}%20\\P(p=x|[s,f])=\frac{T(x)}{\int_{0}^{1}{%20T(t)dt}})
This is a universal formula. When using an emergency, you need to set b = a = 1. BP proponents must in some way choose these parameters so that a plausible beta distribution is obtained. Knowing a and b, you can use PE formulas, for example, to calculate the confidence interval. For example, we chose a = 4.5, b = 20, we have 50 successes and 100 failures, to calculate the confidence interval in the BP, we need to enter 53.5 (50 + 4.5-1) success and 119 failure into the usual formula.
However, we have no selection criteria a and b. The next chapter will tell you how to select them based on static data.
It is most logical to use the mat as a forecast. expectation. Its formula is easily obtained from the mat. beta distribution expectations. We get
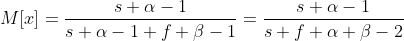 .
.
For example, we have a site with articles. Each of them has a like button. If we sort by the number of likes, then new articles have little chance to kill old ones. If we sort by the ratio of likes to visits, then articles with one entry and one like will interrupt the article with 1000 entries and with 999 likes. It is most reasonable to sort by the last formula, but you need to somehow determine a and b. The easiest way through 2 main points of beta distribution: mat. expectation (how much will be on average) and variance (what is the average deviation from the average).
Let L be the average likelihood of a like. From the expectation of the beta distribution, L = a / (a + b) => a + b = a / L => aL + bL = a => b = a (1 / L - 1). Substitute the dispersion formula:
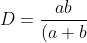^2(a+b+1)}=\frac{a^2(1/L%20-%201)}{(a/L)^2(a/L+1)}=\frac{1/L%20-%201}{(1/L)^2(a/L+1)}%20\\(a/L+1)D=\frac{1/L%20-%201}{(1/L)^2}%20\\a=\frac{1%20-%20L}{(1/L)^2D}-L)
On the pseudo-code, it will look like this:
Despite the fact that this choice of a and b seems objective. This is not rigorous math. First of all, it’s not the fact that the article’s likeability is subject to the Beta distribution, unlike the binomial one, this distribution is “not physical”, it was introduced for convenience. We essentially fitted the curve to the statistics. Moreover, there are several options for fitting .
For example, we conducted an A / B test of several website design options. We got some results and are thinking whether to stop it. If we stop too early we can choose the wrong option, but sometime we still need to stop. We can estimate confidence intervals, but their analysis is complicated. At a minimum, because depending on the significance coefficient, we get different confidence intervals. Now I will show how to calculate the probability that one option is better than all the others.
In addition to dependent events, there are independent events. For such events, P (A | B) = P (A). Therefore, P (AB) = P (B) P (A | B) = P (A) P (B). First you need to show that the options are independent. By the way, comparing confidence intervals is correct only if the options are independent. As already mentioned, proponents of state of emergency discard all data except the experiment itself. Options are separate experiments, so each of them depends only on its results. Therefore they are independent.
For BP, the proof is more complicated, the main point is that a priori “isolates” the options from each other. For example, the events “blue eyes” and “knows Arabic” are dependent, but the events “the Arab knows Arabic” and “the Arab has blue eyes” are not, since the relationship between the first two events is limited to the event “Arab man”. A more correct notation P (p = x) in our case is as follows: P (p = x | apriori = f (x)). Since it all depends on the choice of function a priori. And the events P (p i = x | apriori = f (x)) and P (p j = x | apriori = f (x)) are independent, since the only relationship between them is a priori function.
We introduce the definition of P (p <x), the probability that p is less than x. The formula is obvious:
}=\int_{0}^{x}{P(p=t|[s,f])}%20dt)
We simply “added” all the point probabilities.
Now let's digress, and I will explain to you the formula of complete probability. Let's say there are 3 events A, B, W. The first two events are mutually exclusive and one of them should happen. Those. of these two events, no more and no less than one always occurs. Those. either one event or another should happen, but not together. This is, for example, the gender of a person or the loss of an eagle / tails in one throw. So, Event W can occur only in 2 cases: together with A and together with B. P (W) = P (AW) + P (BW) = P (A) * P (W | A) + P (B) * P (W | B). Similarly, when there are more events. Even when their infinite number. Therefore, we can make such transformations:
=\int_{0}^{1}{P(p=x)P(W|p=x)dx})
Let's say we have n options. We each know the number of successes and failures. [s_1, f_1], ..., [s_n, f_n]. To simplify the recording, we will miss the data from the recording. Those. instead of P (W | [s_1, f_1], ..., [s_n, f_n]) we simply write: P (W). We denote the probability that option i is better than all the others (Chance To Beat All) and carry out some reduction of the record:
=P(best=i))
∀j ≠ i means for any j not equal to i. In simple words, this all means the probability that p i is greater than all the others.
We apply the formula of total probability:
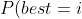%20=\int_{0}^{1}{P(p_i=x)P(best=i|p_i=x)}dx)
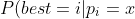%20=\\=P(p_i%3Ep_j,%20\forall%20j\neq%20i%20|p_i=x)%20=\\=P(p_j%3Cx,%20\forall%20j\neq%20i%20|p_i=x)%20=\\=P(p_j%3Cx,%20\forall%20j\neq%20i)%20=\\=\prod_{j\neq%20i}^{{}}{P(p_j%3Cx)})
The first transformation simply changes the form of the record. The second substitutes x instead of p i, since we have a conditional probability. Since p_i is independent of p_j, a third conversion can be performed. As a result, we got that this is equal to the probability that all p_j except i are less than x. Since the options are independent, P (AB) = P (A) * P (B). Those. it all translates into a product of probabilities.
As a result, the formula will take the form:
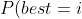=\int_{0}^{1}{P(p_i=x)\prod_{j\neq%20i}^{{}}{P(p_j%3Cx)}}dx)
This can all be calculated in linear time:
For the simple case when there are only two options (Chance to beat baseline / origin, CTBO). Using the normal approximation, this chance can be calculated in constant time . In the general case, it is impossible to solve in constant time. At least Google didn’t succeed. Google WebSite Optimizer had both CTBA and CTBO, after the transfer to Analytics CTBO remained less convenient. The only explanation for this is that there are too many resources spent on CTBA calculation.
By the way, you can understand whether you organized the algorithm correctly in two ways. The total CTBA should be 1. You can also compare your result with screenshots of Google WebSite Optimizer. Here are the comparisons of the results of our free HTraffic Calc statistical calculator with Google WebSite Optimizer.

The difference in the last comparison is due to the fact that I use “smart rounding”. Without rounding, the data is the same.
In general, you can use HTraffic Calc to test your code, because unlike Google WebSite Optimizer, it allows you to enter your data. You can also compare options with it, however, the fundamental features of CTBA should be considered.
If the probability of success is far from 0.5. At the same time, the number of trials (for example, coin tosses or banner displays) in some variants is small and the number of trials differs by several options, then you must either set Apriori or even out the number of trials. The same applies not only to CTBA, but also to comparison of confidence intervals.

As we see from the screenshot, the second option has higher chances to beat the first. This is due to the fact that we have chosen a priori uniform distribution, and his mat expectation is 0.5, this is more than 0.3, therefore, in this case, the option with a smaller number of tests received some bonus. From the point of view of emergency, the experiment is violated - all options should have an equal number of tests. You must align the number of trials by dropping part of the trials from one of the options. Or use the PSU and choose a priori.
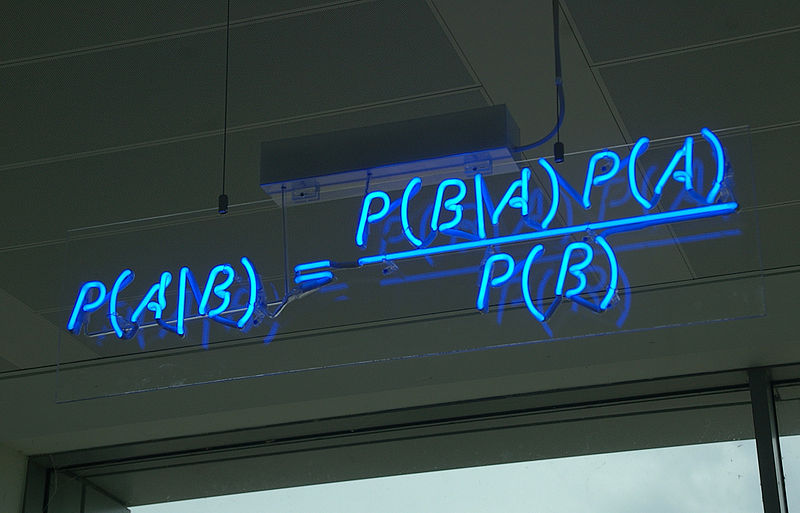
Introduction
Let's start from afar. If the onset of one event increases or decreases the likelihood of another, then such events are called dependent. Terver does not study causation. Therefore, dependent events are not necessarily consequences of each other, the connection may not be obvious. For example, “a person has blue eyes” and “a person knows Arabic” are dependent events, since Arabs have extremely rare blue eyes.
Now we should introduce the notation.
- P (A) means the probability of occurrence of event A.
- P (AB) is the probability of the occurrence of both events together. It does not matter in what order the events P (AB) = P (BA) occur.
- P (A | B) the probability of occurrence of event A, if event B occurred.
Let's think about what is the probability of the occurrence of two events at the same time. P (AB). The probability of the onset of the first event multiplied by the probability of the onset of the second event, in the event of the onset of the first. P (AB) = P (A) P (B | A). Now, if we recall that P (AB) = P (BA). We obtain P (A) P (B | A) = P (B) P (A | B). Move P (B) to the left and get the Bayes formula:
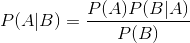
Everything is so simple that a simple priest deduced this formula 300 years ago. But this does not reduce the practical value of this theorem. It allows you to solve the "inverse problem": according to tests to assess the situation.
Direct and inverse problems
The direct problem can be described as follows: for the reason, find the probability of one of the consequences. For example, an absolutely symmetric coin is given (the probability of falling an eagle, like tails, is 1/2). We need to calculate the probability that if we flip a coin twice, an eagle will fall both times. Obviously, it is 1/2 * 1/2 = 1/4.
But the problem is that we only know the probability of this or that event in a minority of cases, almost all of which are artificial, for example, gambling. Moreover, there is nothing absolute in nature, the probability of an eagle falling out of a real coin is 1/2 only approximately. We can say that the direct problem studies some spherical horses in a vacuum.
In practice, the inverse problem is more important: to assess the situation according to the test data. But the problem of the inverse problem is that its solution is more complicated. Mainly due to the fact that our solution will not be the point P = C, but some function P = f (x).
For example, we have a coin, we need to evaluate the probability of tails by experiments. If we tossed a coin 1 time and an eagle fell, this does not mean that eagles always drop. If 2 times tossed and received 2 eagles, then again this does not mean that only eagles fall. To get the exact probability of the tails falling, we must toss a coin an infinite number of times. In practice, this is not possible and we always calculate the probability of an event with some accuracy.
We are forced to use some function. Usually it is customary to denote it as P (p = x | s tails, f eagles) and call it the probability density. This is read as the probability that the probability of an eagle falling is x if, according to the experiment, s tails and f eagles fell out. Sounds complicated sounds due to taftology. It is simpler to consider p some property of a coin, and not probability. And read: so the probability is that p = x ...
Looking ahead, I’ll say that if we throw in the first coin 1000 times and get 500 eagles, and the second 10,000 and get 5000 eagles, then the probability densities will look like this:

Due to the fact that we do not have a point, but a curve, we are forced to use confidence intervals. For example, if they say the 80% confidence interval for p is 45% to 55%, then this means that with 80% probability p will be between 45% and 55%.
Binomial distribution
For simplicity, we consider a binomial distribution. This is the distribution of the number of “successes” in a sequence of a number of independent random experiments, such that the probability of “success” in each of them is constant. It is almost always observed when we have a test sequence with two possible outcomes. For example, when we toss a coin several times, or evaluate the CTR of a banner, or the conversion on a site.
For example, we assume that we need to evaluate the probability of the tails falling out of a coin. We flipped a coin a number of times and got f eagles and s tails. We denote this event as [s, f] and substitute it into the Bayes formula instead of B. The event when p is equal to a certain number will be denoted as p = x and substitute instead of event A.
P ([s, d] | p = x), The probability of getting [s, d] if p = x, provided that p = x we know P ([s, f] | p = x) = K ( f, s) * x ^ s (1-x) ^ f. Where K (f, s) is a binomial coefficient. We get:

We do not know P ([s, f]). And the binomial coefficient is difficult to calculate: there are factorials. But these problems can be solved: the total probability of all possible x should be equal to 1.
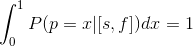
Using simple transformations, we get the formula: This is
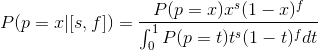
programmed simply, just 10 lines:
//f(x) некоторая функция P(p=x)
m=10000;//число точек
eq=newArray(); //P(p=x|[s,f])
sum=0;
for(i=0;i<m;i++){
x=i/m;// от 0 до 1
eq[i]= f(x) * x^cur.s*(1-x)^cur.f; // С * P(p=x|[s,f]) с точностью до постоянного коефициента
sum+=eq[i]
}
//Сумма должна быть 1for(i=0;i<m;i++)
eq[i]/=sum;
However, P (p = x) remains unknown. It expresses how likely it is that p = x if we do not have experimental data. This function is called a priori. Because of it, there was a holivar in probability theory. We cannot strictly mathematically calculate a priori, only set subjectively. And without a priori, we cannot solve the inverse problem.
Holivar
Proponents of the classical interpretation (frequency approach, emergency), believe that all possible p are equally probable before the experiment. Those. Before the experiment, you need to “forget” the data that we know before. Their opponents, supporters of the Bayesian approach (BP), believe that you need to set some a priori based on our knowledge before the experiment. This is a fundamental difference, even the definition of the concept of probability for these groups is different.
By the way, the creator of this formula, Thomas Bayes, died 200 years earlier than the holivar and has only indirect relation to this dispute. Bayes formula is part of both competing theories.
The frequency approach (PE) is better suited for science where it is necessary to objectively prove a hypothesis. For example, the fact that mortality from a drug is less than a certain threshold. If you need, taking into account all the available information, make a decision, then it is better to use a PSU.
PE is not suitable for forecasting. By the way, confidence interval formulas, consider confidence interval by emergency. BP supporters usually use the Beta distribution as a priori for the binomial distribution, with a = 1 and b = 1 it degenerates into a continuous distribution, which their opponents use. As a result, the formula takes the form:
This is a universal formula. When using an emergency, you need to set b = a = 1. BP proponents must in some way choose these parameters so that a plausible beta distribution is obtained. Knowing a and b, you can use PE formulas, for example, to calculate the confidence interval. For example, we chose a = 4.5, b = 20, we have 50 successes and 100 failures, to calculate the confidence interval in the BP, we need to enter 53.5 (50 + 4.5-1) success and 119 failure into the usual formula.
However, we have no selection criteria a and b. The next chapter will tell you how to select them based on static data.
Forecast
It is most logical to use the mat as a forecast. expectation. Its formula is easily obtained from the mat. beta distribution expectations. We get
For example, we have a site with articles. Each of them has a like button. If we sort by the number of likes, then new articles have little chance to kill old ones. If we sort by the ratio of likes to visits, then articles with one entry and one like will interrupt the article with 1000 entries and with 999 likes. It is most reasonable to sort by the last formula, but you need to somehow determine a and b. The easiest way through 2 main points of beta distribution: mat. expectation (how much will be on average) and variance (what is the average deviation from the average).
Let L be the average likelihood of a like. From the expectation of the beta distribution, L = a / (a + b) => a + b = a / L => aL + bL = a => b = a (1 / L - 1). Substitute the dispersion formula:
On the pseudo-code, it will look like this:
L=0;
L2=0;//Сумма квадратовforeach(articles as article){
p=article.likes/article.shows;
L+=p;
L2+=p^2;
}
n=count(articles);
D=(L2-L^2/n)/(n-1);//Дисперсия
L=L/n;//среднее
a=L^2*(1-L)/D-L;
b=a*(1/L — 1);
foreach(articles as article)
article.forecast=(article.likes+a-1)/(article.shows+a+b-2)
Despite the fact that this choice of a and b seems objective. This is not rigorous math. First of all, it’s not the fact that the article’s likeability is subject to the Beta distribution, unlike the binomial one, this distribution is “not physical”, it was introduced for convenience. We essentially fitted the curve to the statistics. Moreover, there are several options for fitting .
Chance to beat everyone
For example, we conducted an A / B test of several website design options. We got some results and are thinking whether to stop it. If we stop too early we can choose the wrong option, but sometime we still need to stop. We can estimate confidence intervals, but their analysis is complicated. At a minimum, because depending on the significance coefficient, we get different confidence intervals. Now I will show how to calculate the probability that one option is better than all the others.
In addition to dependent events, there are independent events. For such events, P (A | B) = P (A). Therefore, P (AB) = P (B) P (A | B) = P (A) P (B). First you need to show that the options are independent. By the way, comparing confidence intervals is correct only if the options are independent. As already mentioned, proponents of state of emergency discard all data except the experiment itself. Options are separate experiments, so each of them depends only on its results. Therefore they are independent.
For BP, the proof is more complicated, the main point is that a priori “isolates” the options from each other. For example, the events “blue eyes” and “knows Arabic” are dependent, but the events “the Arab knows Arabic” and “the Arab has blue eyes” are not, since the relationship between the first two events is limited to the event “Arab man”. A more correct notation P (p = x) in our case is as follows: P (p = x | apriori = f (x)). Since it all depends on the choice of function a priori. And the events P (p i = x | apriori = f (x)) and P (p j = x | apriori = f (x)) are independent, since the only relationship between them is a priori function.
We introduce the definition of P (p <x), the probability that p is less than x. The formula is obvious:
We simply “added” all the point probabilities.
Now let's digress, and I will explain to you the formula of complete probability. Let's say there are 3 events A, B, W. The first two events are mutually exclusive and one of them should happen. Those. of these two events, no more and no less than one always occurs. Those. either one event or another should happen, but not together. This is, for example, the gender of a person or the loss of an eagle / tails in one throw. So, Event W can occur only in 2 cases: together with A and together with B. P (W) = P (AW) + P (BW) = P (A) * P (W | A) + P (B) * P (W | B). Similarly, when there are more events. Even when their infinite number. Therefore, we can make such transformations:
Let's say we have n options. We each know the number of successes and failures. [s_1, f_1], ..., [s_n, f_n]. To simplify the recording, we will miss the data from the recording. Those. instead of P (W | [s_1, f_1], ..., [s_n, f_n]) we simply write: P (W). We denote the probability that option i is better than all the others (Chance To Beat All) and carry out some reduction of the record:
∀j ≠ i means for any j not equal to i. In simple words, this all means the probability that p i is greater than all the others.
We apply the formula of total probability:
The first transformation simply changes the form of the record. The second substitutes x instead of p i, since we have a conditional probability. Since p_i is independent of p_j, a third conversion can be performed. As a result, we got that this is equal to the probability that all p_j except i are less than x. Since the options are independent, P (AB) = P (A) * P (B). Those. it all translates into a product of probabilities.
As a result, the formula will take the form:
This can all be calculated in linear time:
m=10000;//число точек
foreach(variants as cur){
cur.eq=Array();//P(p=x)
cur.less=Array();//P(p<x)
var sum=0;
for(i=0;i<m;i++){
x=i/m;
cur.eq[i]= x^cur.s*(1-x)^cur.f;//С*P(p=x) с точностью до постоянного коефициента
sum+=cur.eq[i];
cur.less[i]=sum;
}
//сумма всех cur.eq должны быть равны 1for(i=0;i<m;i++){
cur.eq[i]/=sum;
cur.less[i]/=sum;
}
}
//Произведение P_j(p<x)
lessComp=Array();
for(i=0;i<m;i++){
lessComp[i]=1;// заполнить массив единицами
foreach(variants as cur)
lessComp[i]*=cur.less[i];
}
foreach(variants as cur){
cur.ctba=0;//Chance To beat All
for(i=0;i<m;i++)
cur.ctba+=cur.eq[i] * lessComp[i] /cur.less[i];
}For the simple case when there are only two options (Chance to beat baseline / origin, CTBO). Using the normal approximation, this chance can be calculated in constant time . In the general case, it is impossible to solve in constant time. At least Google didn’t succeed. Google WebSite Optimizer had both CTBA and CTBO, after the transfer to Analytics CTBO remained less convenient. The only explanation for this is that there are too many resources spent on CTBA calculation.
By the way, you can understand whether you organized the algorithm correctly in two ways. The total CTBA should be 1. You can also compare your result with screenshots of Google WebSite Optimizer. Here are the comparisons of the results of our free HTraffic Calc statistical calculator with Google WebSite Optimizer.

The difference in the last comparison is due to the fact that I use “smart rounding”. Without rounding, the data is the same.
In general, you can use HTraffic Calc to test your code, because unlike Google WebSite Optimizer, it allows you to enter your data. You can also compare options with it, however, the fundamental features of CTBA should be considered.
CTBA Features
If the probability of success is far from 0.5. At the same time, the number of trials (for example, coin tosses or banner displays) in some variants is small and the number of trials differs by several options, then you must either set Apriori or even out the number of trials. The same applies not only to CTBA, but also to comparison of confidence intervals.

As we see from the screenshot, the second option has higher chances to beat the first. This is due to the fact that we have chosen a priori uniform distribution, and his mat expectation is 0.5, this is more than 0.3, therefore, in this case, the option with a smaller number of tests received some bonus. From the point of view of emergency, the experiment is violated - all options should have an equal number of tests. You must align the number of trials by dropping part of the trials from one of the options. Or use the PSU and choose a priori.
