Network Virtualization in Hyper-V. Configuring an HNV gateway based on Windows Server 2012 R2
In several previous posts about Network Virtualization Technology (Hyper-V Network Virtualization, HNV), I talked about the architecture , settings , and new features of HNV in Windows Server 2012 R2. Today we will talk about perhaps the most difficult topic - building an HNV gateway based on Windows Server 2012 R2 to provide virtualized network segments with access to the outside world. There will be many screenshots.
In most cases, virtual machines (VMs) deployed in virtualized networks need interaction with the outside world - to communicate with other objects of the data center, to access the Internet, to access the corporate network of the company that located these data centers in the data center and so on. With regard to HNV technology, the outside world is anything outside the virtualized network. And before moving on, it is necessary to once again determine the terminology that has slightly changed over the two years of the existence of HNV.
So, the defining concept of HNV is the Customer Network, which has a unique Routing Domain ID (RDID). This is the very virtualized network. There are several synonyms for the Customer Network, depending on which tool you use:
But all these terms are the essence of the Customer Network. Each customer’s network consists of one or more virtual subnets (Virtual Subnet), and each virtual subnet has its own unique 24-bit VSID. Packet routing between VMs belonging to the same customer’s network is carried out automatically, regardless of whether these machines are located on the same virtual subnet or on different, on the same physical host, or on different. But if you need communication with the outside world, that is, you need to transfer packets outside the Customer Network, then an HNV gateway (HNV Gateway, HNVGW) must be configured.
An HNV gateway can be either a turnkey hardware solution or a host based on Windows Server 2012 R2. Currently, three hardware solutions are available on the market:
In this post, I will focus on creating a Windows Server 2012 R2-based HNV gateway, while managing the HNV on my demo network, including setting up the gateway, will be done using System Center 2012 R2 Virtual Machine Manager (VMM). Using the VMM abbreviation below, I assume it is version R2, unless explicitly stated otherwise.
Let me remind you that strictly speaking, HNV is a technology of Windows Server 2012 and higher, and it can be configured without VMM, simply using PowerShell cmdlets. I provide links to examples of relevant scripts without and using an HNV gateway. But in real-world scenarios, VMM is used to manage the HNV, which assumes the role of centralized storage and distribution of HNV policies.
Architecturally, the Windows Server 2012 R2-based HNV gateway is a physical host running one or more VMs that route packets from virtualized networks to the outside world and vice versa. Please note, this is the physical host. Implementing an HNV gateway simply as a virtual machine will fail even if only because the encapsulation of packets (see the post about the HNV concept) requires the Hyper-V role, and Hyper-V does not support nested virtualization.
In fairness, it is worth noting that, technically, a gateway can also be built on the basis of Windows Server 2012. But at the same time, firstly, a gateway with Windows Server 2012 will require running as many VMs as you have Customer Networks, and scaling such a solution is difficult. Secondly, to manage such a gateway using VMM, you will need to write a provider for VMM. Using Windows Server 2012 R2 + System Center 2012 R2 Virtual Machine Manager is an almost out of the box HNV gateway. Windows Server 2012 R2 implements a multi-tenant gateway that allows you to use one VM to route the traffic of various virtualized networks, and System Center 2012 R2 Virtual Machine Manager already has a provider to manage this gateway.
What are the options for the HNV gateway? There are two of them.
The first option implements traffic routing from the Customer Network to the data center network, and routing can be either direct or address translation (NAT).
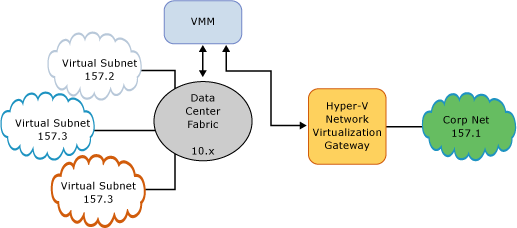
The figure shows direct routing, which makes sense if the spaces of CA addresses of different tenants (Customer Networks) do not intersect and they need access to the corporate network. Or, as in the figure, there is only one tenant with several subnets. For a private cloud, when tenants, for example, are virtualized networks of various departments of a large enterprise, a completely possible option.
When using NAT, each tenant of the HNV gateway associates a dedicated IP address on its external interface, and all packets from tenant virtual machines are sent to the outside world with this dedicated IP in the "Sender's IP address" field.
The second option involves the construction of a network-to-network tunnel from the HNV gateway to the required point, for example, via the Internet to the customer’s corporate network.

This is just a typical hosting scenario, when the customer’s VMs are located in the host’s data center and communicate via VPN with the customer’s network. At the same time, HNV technology allows the customer to save IP settings and not be afraid for the software to work inside the VM, and the hoster can place virtual machines with the IP necessary for the customer, isolating these virtual machines from other VMs and not setting up VLANs.
Concluding the architectural section of the post, I’ll briefly note what is the multi-tenant nature of the gateway based on Windows Server 2012 R2.
Imagine that the data center has virtualized the networks of two customers, Contoso and Woodgroveusing exactly the same CA spaces: 10.0.0.0/24. How to "separate" packages of these customers on the HNV gateway? The first possible solution is to create your own VM on the gateway for each customer and specify it in the settings of the corresponding customer network as the default gateway. Thus, packets sent to the outside world from Contoso will always come to the network interface of one VM of a gateway, packets from Woodgrove will always come to the interface of a second VM, etc. As mentioned, a gateway based on Windows Server 2012 would use just such an approach .

In Windows Server 2012 R2, the ability to use so-called compartments has appeared for routing. In the virtual machine, for each tenant, a certain “cell” object is created, which includes virtual network interfaces, IP addresses, routing table, ARP table, etc. Elements of one cell are isolated from elements of another cell. Thus, packet routing from Contoso is carried out within the corresponding cell and does not overlap; it does not affect the routing of Woodgrove packets in another cell, even if the entries in the routing tables of these cells look the same. This approach allows using one VM for routing packets of different tenants without any conflicts.

As can be seen in fig. above, there is a default compartment, which includes the network settings specified when creating the VM, and two cells for tenants that appeared during the configuration of the HNV gateway.
Having reinforced the theory, we proceed directly to the creation of the gateway. For simplicity, I will consider the option of a gateway without clustering, although it is clear that in a real data center such an important element of virtualization involves working in high availability mode. A detailed document on how to make the HNV gateway highly available can be found here .
The basic steps to create a gateway include the following:
Let's go in order.
This item is described in some detail in one of the previous posts , so I’ll only show you how logical and virtual networks look in my Contoso laboratory candlestick data center.

For our task, we need three logical networks: an external segment (Contoso_External_LN01), a network for gateway management (Contoso_Management_LN01) and a network (Contoso_HNV_LN01), on top of which virtualized networks are actually created. The IP pool of the network Contoso_HNV_LN01 defines the PA space, and in the properties of this network a checkbox must be marked that allows the use of HNV technology.

VM networks (VM Networks, they are also customer networks, they are Customer Networks) look like this:

You see two VM networks for Adatum and Fabrikamusing intersecting address space (10.30.1.0/24). The Gateway Connection column shows that so far none of the VM networks uses a gateway.
In general, any host running Windows Server 2012 R2 that VMM manages can be configured as an HNV gateway. In a good way, this host should have several physical network interfaces looking at the desired segments (external, management segment, HNV segment). However, it follows from the architectural part of the post that the VM itself is involved in routing packets in the gateway. Therefore, how many physical network cards should be in the host acting as a gateway is determined by the issues of performance, reliability (you can use timing, for example) and, of course, the logic of how and where you want to send packets. Specifically, in my stand, the host gateway contains only one physical network interface, for now this is enough for me to experiment.
But in any case, in the properties of the host selected for the gateway role, you should set this checkbox here.

It will prevent any “ordinary” VMs that use HNV from starting on the gateway. In a real situation, you are unlikely to run anything else on the gateway except the components of the gateway itself.
Now let's talk about the very VM that will route packets using compartments. The easiest way to deploy it is with a service template. In this case, you can immediately tell VMM that the RRAS service was raised in it when deploying the VM, so that two machines on the cluster were lifted for high availability of such machines, etc. But, firstly, we agreed to do everything by hand to better understand what happens, secondly, service templates do not support second-generation VMs that are deployed, and work faster.
Therefore, I created a second-generation VM template based on VHDX with a Windows Server 2012 R2 image. There is nothing unusual in this process, I will only show the network settings in the template.

You see three virtual network adapters (vNICs): one is connected to an external network (see. Fig.), The second to the management network, the third can be left in the Not Not connected state in the template , and during or immediately after VM deployment, connect it through the virtual A switch (Hyper-V Extensible Switch) to a network that uses HNV. Typically, when describing a gateway, this network is called Backend.
We now deploy the VM based on this template to the host that we selected and configured as the gateway in the previous paragraph. Pay attention to the name you give to this VM. It will be needed later in the configuration of the gateway.
After the VM is deployed, let's go into it, connect the network adapter to the Backend network, turn off the Firewall and rename the network adapters for convenience so that the names reflect their purpose, for example

Now in the VM (I called it GatewayVM01 ), you need to set the Remote Access role . This is done standardly through Server Manager , Manage -> Add Roles and Features . Click Next until we get to the choice of a role, select Remote Access , then Next again until we get to Role Services , where we mark two services.

Click Next and Install to the stop.. After the installation is completed, click on the Open the Getting Started Wizard

and in the window of the wizard that opens, select Deploy VPN only .

As a result, the well-known RRAS console opens, which shows that the service has not yet been configured.

Thus, we have configured the host and the corresponding VM, and now everything is ready to add this “workpiece” as an HNV gateway to the VMM console for further configuration.
In the VMM console, go to the Fabric section , click Add Resources and select Network Service . On the first page of the wizard, we give the gateway a meaningful name and description.

Then we select Microsoft as the manufacturer and Microsoft Windows Server Gateway in the list of models.

On the Credentials page , select Run As account to access the device. This entry must have administrative rights to the gateway VM. In our case, the VM was not included in the domain, therefore, we indicate the entry with the password of the local administrator. If there is no such record in VMM, you can create it right there.

Perhaps the most interesting parameter is the connection string (Connection String ), in which, using the three parameters VMHost , GatewayVM, and BackendSwitch, you need to specify the host name and “workpiece” VM and the name of the virtual switch on the host through which the VM connects to the Backend network. Please note that there are no spaces in the connection string; the separator is a semicolon ( ; ).

In addition to the three listed above, there are several more parameters, a description of which can be found here (see clause 16). In particular, DirectRoutingMode = True will configure the gateway to work in direct routing mode.
With the connection string specified above, certificates are not used, therefore, on the Certificates pagejust click Next .
On the Provider page, click the Test button and make sure that all tests pass without errors.

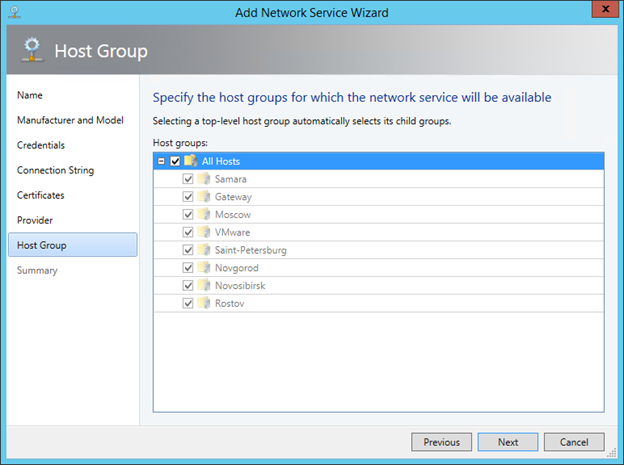
On the Host Group page, specify which host groups can use this gateway.
Check the settings on the Summary page , and if everything is correct, click Finish .

Verify that the related tasks in the Jobs section have completed successfully. It remains to configure the network interfaces of the newly created HNV gateway. In the Fabric -> Networking -> Network Service section of the VMM console, right-click the gateway, selectProperties and go to the Connectivity tab . Here you need to enable Front End Connection and Back End Connection and select the correct VM network adapters and the corresponding logical subnet sites.

Now VMM knows which gateway VM adapters are for what purpose, and will properly configure the RRAS service inside this VM. When jobs are completed, in the RRAS console of the gateway VM, you will see that the service is running and works as a multi-tenant gateway.

The point is small, configure the required VM networks to use the created HNV gateway.
In the VMM console, go to the VMs and Services section , click VM Networks , select the desired VM network and click the Properties button . We go to the Connectivity tab and enable the use of the HNV gateway by this network. For a Fabrikam network , for example, enable NAT.

VMM will automatically allocate from the IP pool of the logical network associated with the external interface of the HNV gateway the address to which the addresses of the senders of all packets from the Fabrikam network will be broadcast . But you can manually select IP from the pool by specifying it in the IP address field

By closing the properties window, at the bottom of the VMM console, you can see what specific external address is used for this VM network

We do the same for the Adatum network and all other virtualized networks that need external access with NAT support.
Now let's see how the connection to the outside world via VPN is configured, that is, we implement the Hybrid Cloud (Site to site VPN) scenario. At the same time, I assume that the VPN device in the corporate network is already configured, uses IKEv2 protocol and Preshared Key authentication, which is typical for network-to-network tunnels, and we know its external IP.
In the properties of the same Fabrikam VM network, on the already familiar Connectivity tab, mark the top checkbox.
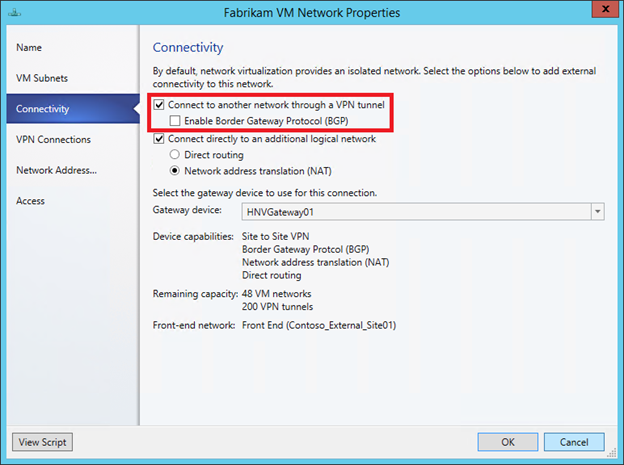
In this case, a new VPN Connections tab appears in the VM network properties window , where you need to click Addadd a VPN connection, specify its name and IP address of the VPN device to which the tunnel is built

In the Authentication section, specify the prepared Run As account entry with the Prescribed Key,

and in the Routes section we write the necessary routes, for example,

As you might have noticed, for dynamic route updates implemented BGP support.
You can look at the advanced settings in Advanced , say change the VPN protocol or encryption settings, but if none of this is required, then click OK. At the bottom of the VMM console for the configured VM network, something like Now will be displayed as

soon as from any VM running on a virtualized networkFabrikam , try pinging the address from the subnet specified with the VPN tunnel settings, for example, 10.30.50.101, the HNV gateway will open the tunnel and establish a connection with the specified VPN device, and through it with the corporate network

Done!
If the information from this post was not enough, you can use the detailed step- by -step guide to create a laboratory stand.
One question remains open, how does packet routing actually occur when using the HNV gateway, what does it look like inside the gateway? But this is already a level of difficulty of 400 for the most sophisticated. :) Although, if any, I’m ready to write.
Hope the material was helpful.
Thanks!
In most cases, virtual machines (VMs) deployed in virtualized networks need interaction with the outside world - to communicate with other objects of the data center, to access the Internet, to access the corporate network of the company that located these data centers in the data center and so on. With regard to HNV technology, the outside world is anything outside the virtualized network. And before moving on, it is necessary to once again determine the terminology that has slightly changed over the two years of the existence of HNV.
Terminology
So, the defining concept of HNV is the Customer Network, which has a unique Routing Domain ID (RDID). This is the very virtualized network. There are several synonyms for the Customer Network, depending on which tool you use:
- in VMM, this is VM Network;
- in PowerShell, this is a Routing Domain;
- in many articles and blogs, it’s Tenant or Tenant Virtual Network.
But all these terms are the essence of the Customer Network. Each customer’s network consists of one or more virtual subnets (Virtual Subnet), and each virtual subnet has its own unique 24-bit VSID. Packet routing between VMs belonging to the same customer’s network is carried out automatically, regardless of whether these machines are located on the same virtual subnet or on different, on the same physical host, or on different. But if you need communication with the outside world, that is, you need to transfer packets outside the Customer Network, then an HNV gateway (HNV Gateway, HNVGW) must be configured.
Gateway Implementation Options
An HNV gateway can be either a turnkey hardware solution or a host based on Windows Server 2012 R2. Currently, three hardware solutions are available on the market:
- from nAppliance
- from Iron Networks
- from F5
In this post, I will focus on creating a Windows Server 2012 R2-based HNV gateway, while managing the HNV on my demo network, including setting up the gateway, will be done using System Center 2012 R2 Virtual Machine Manager (VMM). Using the VMM abbreviation below, I assume it is version R2, unless explicitly stated otherwise.
Let me remind you that strictly speaking, HNV is a technology of Windows Server 2012 and higher, and it can be configured without VMM, simply using PowerShell cmdlets. I provide links to examples of relevant scripts without and using an HNV gateway. But in real-world scenarios, VMM is used to manage the HNV, which assumes the role of centralized storage and distribution of HNV policies.
Gateway architecture
Architecturally, the Windows Server 2012 R2-based HNV gateway is a physical host running one or more VMs that route packets from virtualized networks to the outside world and vice versa. Please note, this is the physical host. Implementing an HNV gateway simply as a virtual machine will fail even if only because the encapsulation of packets (see the post about the HNV concept) requires the Hyper-V role, and Hyper-V does not support nested virtualization.
In fairness, it is worth noting that, technically, a gateway can also be built on the basis of Windows Server 2012. But at the same time, firstly, a gateway with Windows Server 2012 will require running as many VMs as you have Customer Networks, and scaling such a solution is difficult. Secondly, to manage such a gateway using VMM, you will need to write a provider for VMM. Using Windows Server 2012 R2 + System Center 2012 R2 Virtual Machine Manager is an almost out of the box HNV gateway. Windows Server 2012 R2 implements a multi-tenant gateway that allows you to use one VM to route the traffic of various virtualized networks, and System Center 2012 R2 Virtual Machine Manager already has a provider to manage this gateway.
What are the options for the HNV gateway? There are two of them.
Private Cloud (Routing)
The first option implements traffic routing from the Customer Network to the data center network, and routing can be either direct or address translation (NAT).

The figure shows direct routing, which makes sense if the spaces of CA addresses of different tenants (Customer Networks) do not intersect and they need access to the corporate network. Or, as in the figure, there is only one tenant with several subnets. For a private cloud, when tenants, for example, are virtualized networks of various departments of a large enterprise, a completely possible option.
When using NAT, each tenant of the HNV gateway associates a dedicated IP address on its external interface, and all packets from tenant virtual machines are sent to the outside world with this dedicated IP in the "Sender's IP address" field.
Hybrid Cloud (Site to site VPN)
The second option involves the construction of a network-to-network tunnel from the HNV gateway to the required point, for example, via the Internet to the customer’s corporate network.

This is just a typical hosting scenario, when the customer’s VMs are located in the host’s data center and communicate via VPN with the customer’s network. At the same time, HNV technology allows the customer to save IP settings and not be afraid for the software to work inside the VM, and the hoster can place virtual machines with the IP necessary for the customer, isolating these virtual machines from other VMs and not setting up VLANs.
Concluding the architectural section of the post, I’ll briefly note what is the multi-tenant nature of the gateway based on Windows Server 2012 R2.
Imagine that the data center has virtualized the networks of two customers, Contoso and Woodgroveusing exactly the same CA spaces: 10.0.0.0/24. How to "separate" packages of these customers on the HNV gateway? The first possible solution is to create your own VM on the gateway for each customer and specify it in the settings of the corresponding customer network as the default gateway. Thus, packets sent to the outside world from Contoso will always come to the network interface of one VM of a gateway, packets from Woodgrove will always come to the interface of a second VM, etc. As mentioned, a gateway based on Windows Server 2012 would use just such an approach .

In Windows Server 2012 R2, the ability to use so-called compartments has appeared for routing. In the virtual machine, for each tenant, a certain “cell” object is created, which includes virtual network interfaces, IP addresses, routing table, ARP table, etc. Elements of one cell are isolated from elements of another cell. Thus, packet routing from Contoso is carried out within the corresponding cell and does not overlap; it does not affect the routing of Woodgrove packets in another cell, even if the entries in the routing tables of these cells look the same. This approach allows using one VM for routing packets of different tenants without any conflicts.

As can be seen in fig. above, there is a default compartment, which includes the network settings specified when creating the VM, and two cells for tenants that appeared during the configuration of the HNV gateway.
Gateway Creation
Having reinforced the theory, we proceed directly to the creation of the gateway. For simplicity, I will consider the option of a gateway without clustering, although it is clear that in a real data center such an important element of virtualization involves working in high availability mode. A detailed document on how to make the HNV gateway highly available can be found here .
The basic steps to create a gateway include the following:
- setting up logical networks and VM networks;
- configure host for gateway role
- VM preparation for the gateway
- adding a gateway to VMM
- gateway settings for specific VM networks
Let's go in order.
Configure logical networks and VM networks
This item is described in some detail in one of the previous posts , so I’ll only show you how logical and virtual networks look in my Contoso laboratory candlestick data center.

For our task, we need three logical networks: an external segment (Contoso_External_LN01), a network for gateway management (Contoso_Management_LN01) and a network (Contoso_HNV_LN01), on top of which virtualized networks are actually created. The IP pool of the network Contoso_HNV_LN01 defines the PA space, and in the properties of this network a checkbox must be marked that allows the use of HNV technology.

VM networks (VM Networks, they are also customer networks, they are Customer Networks) look like this:

You see two VM networks for Adatum and Fabrikamusing intersecting address space (10.30.1.0/24). The Gateway Connection column shows that so far none of the VM networks uses a gateway.
Configure host for gateway role
In general, any host running Windows Server 2012 R2 that VMM manages can be configured as an HNV gateway. In a good way, this host should have several physical network interfaces looking at the desired segments (external, management segment, HNV segment). However, it follows from the architectural part of the post that the VM itself is involved in routing packets in the gateway. Therefore, how many physical network cards should be in the host acting as a gateway is determined by the issues of performance, reliability (you can use timing, for example) and, of course, the logic of how and where you want to send packets. Specifically, in my stand, the host gateway contains only one physical network interface, for now this is enough for me to experiment.
But in any case, in the properties of the host selected for the gateway role, you should set this checkbox here.

It will prevent any “ordinary” VMs that use HNV from starting on the gateway. In a real situation, you are unlikely to run anything else on the gateway except the components of the gateway itself.
Preparing a VM for a Gateway
Now let's talk about the very VM that will route packets using compartments. The easiest way to deploy it is with a service template. In this case, you can immediately tell VMM that the RRAS service was raised in it when deploying the VM, so that two machines on the cluster were lifted for high availability of such machines, etc. But, firstly, we agreed to do everything by hand to better understand what happens, secondly, service templates do not support second-generation VMs that are deployed, and work faster.
Therefore, I created a second-generation VM template based on VHDX with a Windows Server 2012 R2 image. There is nothing unusual in this process, I will only show the network settings in the template.

You see three virtual network adapters (vNICs): one is connected to an external network (see. Fig.), The second to the management network, the third can be left in the Not Not connected state in the template , and during or immediately after VM deployment, connect it through the virtual A switch (Hyper-V Extensible Switch) to a network that uses HNV. Typically, when describing a gateway, this network is called Backend.
We now deploy the VM based on this template to the host that we selected and configured as the gateway in the previous paragraph. Pay attention to the name you give to this VM. It will be needed later in the configuration of the gateway.
After the VM is deployed, let's go into it, connect the network adapter to the Backend network, turn off the Firewall and rename the network adapters for convenience so that the names reflect their purpose, for example

Now in the VM (I called it GatewayVM01 ), you need to set the Remote Access role . This is done standardly through Server Manager , Manage -> Add Roles and Features . Click Next until we get to the choice of a role, select Remote Access , then Next again until we get to Role Services , where we mark two services.

Click Next and Install to the stop.. After the installation is completed, click on the Open the Getting Started Wizard

and in the window of the wizard that opens, select Deploy VPN only .

As a result, the well-known RRAS console opens, which shows that the service has not yet been configured.

Thus, we have configured the host and the corresponding VM, and now everything is ready to add this “workpiece” as an HNV gateway to the VMM console for further configuration.
Adding a Gateway to VMM
In the VMM console, go to the Fabric section , click Add Resources and select Network Service . On the first page of the wizard, we give the gateway a meaningful name and description.

Then we select Microsoft as the manufacturer and Microsoft Windows Server Gateway in the list of models.

On the Credentials page , select Run As account to access the device. This entry must have administrative rights to the gateway VM. In our case, the VM was not included in the domain, therefore, we indicate the entry with the password of the local administrator. If there is no such record in VMM, you can create it right there.

Perhaps the most interesting parameter is the connection string (Connection String ), in which, using the three parameters VMHost , GatewayVM, and BackendSwitch, you need to specify the host name and “workpiece” VM and the name of the virtual switch on the host through which the VM connects to the Backend network. Please note that there are no spaces in the connection string; the separator is a semicolon ( ; ).

In addition to the three listed above, there are several more parameters, a description of which can be found here (see clause 16). In particular, DirectRoutingMode = True will configure the gateway to work in direct routing mode.
With the connection string specified above, certificates are not used, therefore, on the Certificates pagejust click Next .
On the Provider page, click the Test button and make sure that all tests pass without errors.

On the Host Group page, specify which host groups can use this gateway.

Check the settings on the Summary page , and if everything is correct, click Finish .

Verify that the related tasks in the Jobs section have completed successfully. It remains to configure the network interfaces of the newly created HNV gateway. In the Fabric -> Networking -> Network Service section of the VMM console, right-click the gateway, selectProperties and go to the Connectivity tab . Here you need to enable Front End Connection and Back End Connection and select the correct VM network adapters and the corresponding logical subnet sites.

Now VMM knows which gateway VM adapters are for what purpose, and will properly configure the RRAS service inside this VM. When jobs are completed, in the RRAS console of the gateway VM, you will see that the service is running and works as a multi-tenant gateway.

The point is small, configure the required VM networks to use the created HNV gateway.
Gateway configuration for specific VM networks
In the VMM console, go to the VMs and Services section , click VM Networks , select the desired VM network and click the Properties button . We go to the Connectivity tab and enable the use of the HNV gateway by this network. For a Fabrikam network , for example, enable NAT.

VMM will automatically allocate from the IP pool of the logical network associated with the external interface of the HNV gateway the address to which the addresses of the senders of all packets from the Fabrikam network will be broadcast . But you can manually select IP from the pool by specifying it in the IP address field

By closing the properties window, at the bottom of the VMM console, you can see what specific external address is used for this VM network

We do the same for the Adatum network and all other virtualized networks that need external access with NAT support.
Now let's see how the connection to the outside world via VPN is configured, that is, we implement the Hybrid Cloud (Site to site VPN) scenario. At the same time, I assume that the VPN device in the corporate network is already configured, uses IKEv2 protocol and Preshared Key authentication, which is typical for network-to-network tunnels, and we know its external IP.
In the properties of the same Fabrikam VM network, on the already familiar Connectivity tab, mark the top checkbox.

In this case, a new VPN Connections tab appears in the VM network properties window , where you need to click Addadd a VPN connection, specify its name and IP address of the VPN device to which the tunnel is built

In the Authentication section, specify the prepared Run As account entry with the Prescribed Key,

and in the Routes section we write the necessary routes, for example,

As you might have noticed, for dynamic route updates implemented BGP support.
You can look at the advanced settings in Advanced , say change the VPN protocol or encryption settings, but if none of this is required, then click OK. At the bottom of the VMM console for the configured VM network, something like Now will be displayed as

soon as from any VM running on a virtualized networkFabrikam , try pinging the address from the subnet specified with the VPN tunnel settings, for example, 10.30.50.101, the HNV gateway will open the tunnel and establish a connection with the specified VPN device, and through it with the corporate network

Done!
If the information from this post was not enough, you can use the detailed step- by -step guide to create a laboratory stand.
One question remains open, how does packet routing actually occur when using the HNV gateway, what does it look like inside the gateway? But this is already a level of difficulty of 400 for the most sophisticated. :) Although, if any, I’m ready to write.
Hope the material was helpful.
Thanks!
