What should we build a network
- Tutorial
When you use complex algorithms to solve computer vision problems, you need to know the basics. Ignorance of the basics leads to stupid errors, to the fact that the system produces an unverifiable result. You use OpenCV, and then you guess: "maybe if you made everything specifically for my task with pens would be much better?". Often, the customer puts the condition “you cannot use third-party libraries,” or when work is in progress for some kind of microcontroller, everything needs to be skipped from scratch. This is where the bummer comes in: in the foreseeable future it’s really possible to do something, only knowing how the basics work. However, reading articles is often not enough. To read the article about number recognition and try to do it yourself is a huge chasm. Therefore, personally, I try to periodically write some simple little programs, including a maximum of new and unknown algorithms for me + training old memories. The story is about one of such examples, which I wrote in a couple of evenings. It seemed to me that a quite nice set of algorithms and methods, allowing to achieve a simple evaluative result, which I have never seen.

Sitting in the evening and suffering from the need to do something useful, but I don’t feel like it, I came across another article on neural networks and caught fire. Finally, you need to make your own neural network. The idea is commonplace: everyone loves neural networks, there are tons of open source examples. I sometimes had to use both LeNet and OpenCV networks. But I was always alarmed that their characteristics and mechanics I know only by pieces of paper. And between the knowledge of “neural networks are taught using the backpropagation method” and the understanding of how to do this, there is a huge gap. And then I decided. It's time to sit for 1-2 evenings and do it yourself, figure it out and understand.
A neural network without a puzzle that a horse without a rider. To solve a serious problem made on a knee by a neural network is to spend a lot of time on debugging and processing. Therefore, a simple task was needed. One of the simplest tasks in signal processing that can be solved purely mathematically is the problem of detecting white noise. The plus of the problem is precisely that it can be solved on a piece of paper, you can evaluate the accuracy of the resulting network in comparison with a mathematical solution. After all, not in every task it is possible to evaluate how well the neural network worked just by checking the formula.
To begin, we formulate the problem. Suppose we have a sequence of N elements. In each of the elements of the sequence there is noise, with zero expectation and a single dispersion. There is a signal E, which can be in this sequence with a center from 0.5 to N-0.5. We set the signal with a Gaussian with such a dispersion that, when located in the center of the pixel, most of the energy is in the same pixel (it will be boring with a very point one). It is necessary to decide whether there is a signal in the sequence or not.
“What a synthetic task!” You say. But it is not so. This problem arises every time you work with point objects. It can be stars in the image, it can be a reflected radio (sound, optical) pulse in a time sequence, it can even be some microorganisms under a microscope, not to mention planes and satellites in a telescope.
We write a little more strictly. Let there be a sequence of signals l 0 ... I n containing normal noise with constant dispersion and zero mathematical expectation: The
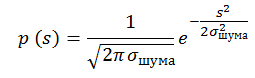
probability that a pixel contains a signal s is equal to p (s). An example of a sequence filled with normally distributed noise with dispersion 1 and expectation 0:

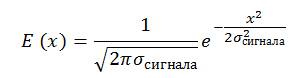
There is also a signal with a constant signal-to-noise ratio, SNR = E_signal / σ_noise = const. We have the right to write this when the signal size is approximately equal to the pixel size. The signal is also set by us by a Gaussian:
For simplicity, we assume that the signal σ_ = 0.25 ∙ L, where L is the pixel size. And this means that for a signal located in the center of the pixel, the pixel will contain the signal energy from - 2σ to + 2σ:
This is how the last sequence with noise looks like, on top of which a signal is superimposed with SNR = 5 centered at 4.1:

By the way, and do you know how to generate a normal distribution ?
It's funny, but many use the central limit theorem to generate it.. In this method, 6 linearly distributed values are added in the range of -0.5 to 0.5. It is believed that the resulting value is distributed normally with a dispersion of unity. But this method gives incorrect distribution tails, with large deviations. If we take exactly 6 quantities, then max = | min | = 3 = 3 * σ. Which immediately cuts off 0.2% of implementations. When generating a 100 * 100 image, such events should occur in 20 pixels, which is not so small.
There are good algorithms: The Box-Muller , Converting George Marsaglia
Habré has a good article on this topic.
All these methods are based on the mathematical transformation of the linear distribution on the interval [0; 1] into the normal distribution.
A lot has been written about the neural network. I will try not to go into details, limiting myself only to links and main points.
A neural network consists of neurons. Nobody knows exactly how a neuron is arranged in a person, but there are many beautiful models. On a habr there were many interesting articles about neurons: 1 , 2 , etc.
In the problem, I took as a basis the simplest scheme of neurons, when a sequence of signals is fed to the input of a neuron, which is summed up and run through the activation function:
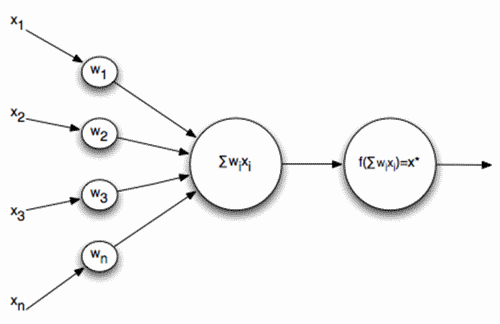
Where is the activation function:
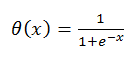
What does such a neuron do in such a model and why does it need an activation function?
A neuron compares with a certain pattern for which it is trained. And the activation function is a trigger that makes a decision on how much the pattern matches and normalizes the solution. For some reason, it often seems to me that a neuron looks like a transistor, but this is a digression:
Why not make the activation function a step? There are many reasons, but the main one, which will be discussed a little later, is a learning feature that requires differentiation of the neuron function. The above activation function has a very good differential:

We have a network. How to solve the problem? The classic way to solve a simple problem is to create a neural network of this kind:
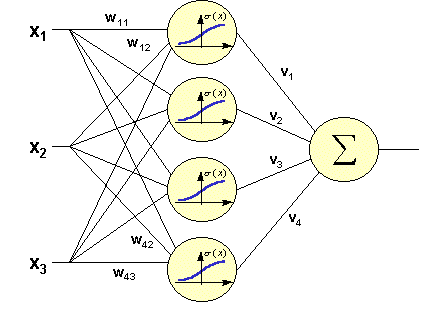
It has an input signal, one hidden layer (where each neuron is connected to all input elements) and an output neuron. Training such a network is, in fact, setting up all the coefficients w and v.
We will do almost this, but after optimizing for the task. Why train every neuron of the hidden layer for every pixel of the input image? The maximum signal takes three pixels, and most likely even two. Therefore, we connect each neuron of the hidden layer with only three neighboring pixels:
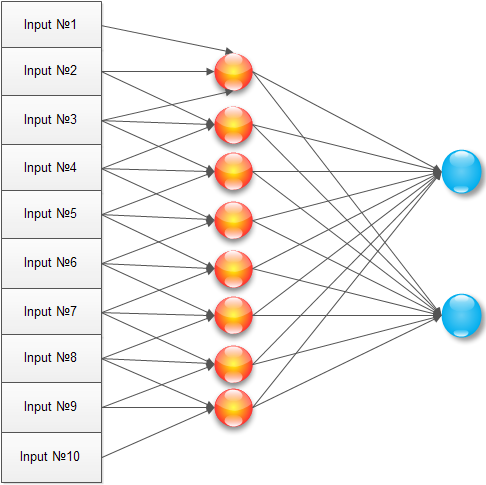
With this configuration, the neuron is trained in the vicinity of the image, starting to work as a local detector. An array of trained elements for the hidden layer (1..N) will look like:
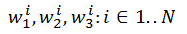
As an experiment, I introduced two output neurons, but as it turned out later, this did not make much sense.
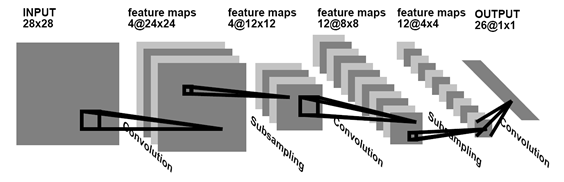
This type of neural network is one of the oldest used in the work. Recently, more and more people are using convolutional networks. About convolution networks already repeatedly wrote on a habr: 1 , 2 .
A convolutional network is a network that searches and remembers existing patterns that are universal for the entire image. Usually, to demonstrate what a neural network is, they draw an image like this:
But when you start trying to code it, the brain goes into a stupor of "how can this be applied to reality." But in reality, the above example of a neural network is translated into a convolutional network with just one action. To do this, when learning, it is enough to assume that the elements w 1 1 , ..., w 1 N are not different elements, but the same element w 1 . Then, as a result of training the hidden layer, only three elements w 1 , w 2 , w 3 will be found , which are a convolution.
True, as it turned out, one convolution is not enough to solve the problem, you need to enter a second one, but this is easy to do by increasing the number of elements in the hidden layer to 1..2N, while the elements 1..N train the first convolution, and the elements N .. 2N is the second.
A neural network is simple to draw, but not so simple to train. When you do this for the first time, the brain turns a little. But, fortunately, there are two very good articles in Runet, after which everything becomes clear as a day: 1 , 2
The first illustrates very well the logic and order of learning, the second is a well-described mathematical essence: where does what comes from formulas, how does the neural network get initialized how to correctly calculate and apply the coefficients.
In general, the method of back propagation of the error is as follows: apply a known signal to the input, distribute it to the output neurons, compare with the desired result. If there is a mismatch, then the error value is multiplied by the weight of the connection and passed to all neurons on the last layer. When all neurons know their error, then shift their learning coefficients so that the error decreases.
If anything, then you should not be afraid of learning. For example, the error definition is made in one line like this:
And the correction of weights like this:
To begin with, as promised, we calculate "what should be." Suppose we have an SNR (signal to noise) ratio of 3. In this case, the signal is 3 times higher than the noise variance. Let's draw the probability that the signal in the pixel takes the value X:
The graph immediately shows the graphs only for the probability distribution of noise and the graph of the probability distribution of signal + noise at a point with the ratio SNR = 3. In order to make a decision on finding a signal, you need to select a certain Xs, consider all values greater than it as a signal, all values less than noise. We will draw the probability that we made a decision about false alarm and skipping an object (for the red graph this is its integral, for the blue “1-integral”):
The intersection point for such graphs is usually called the EER (Equal Error Rate). At this point, the probability of an incorrect decision is equal to the probability of losing the object.
In this problem, we have 10 input signals. How to choose an EER point for such a situation? Simple enough. The probability that a false alarm does not occur at the selected value of Xs will be equal to (the integral in the blue graph from the first figure):
Accordingly, the probability that a false alarm does not occur at 10 pixels is equal to: The
probability that at least 1 false alarm occurs is equal to 1 -P. We draw the 1-P graph and, next to it, the graph of the object skip probability (duplicate from the second graph):
Therefore, the EER point for the signal and noise at SNR = 3 is in the region of the two and EER≈0.2 in it. And what will the neural network give?
It can be seen that the neural network will be slightly worse than the problem solved on the fingers. But it is not all that bad. In mathematical consideration, we did not take into account several features (for example, the signal may not go to the center of the pixel). Without going particularly deeply, we can say that this does not significantly worsen the statistics, but it worsens.
To be honest, I was encouraged by this result. The network copes well with a purely mathematical problem.
Nevertheless, my main task was to create a neural network from scratch and poke a wand into it. In this section there will be a couple of funny gifs about the behavior of the network. The network turned out to be far from ideal (I think that the article will be accompanied by crushing comments by professionals, because this topic is popular on Habré), but I learned a lot of design and writing features as a result of writing and from now on I will try not to repeat it, so I'm personally pleased.
The first GIF for a regular network. The upper bar is the input signal in time. SNR = 10, the signal is clearly visible. The lower two strips are the entrance to the summation of the last neuron. It is seen that the network stabilized the image and when the signal is turned on or off, only the contrast of the inputs of the last neuron changes. It is funny that in the absence of a signal the image is almost stationary.
The second GIF is the same for the convolution network. The number of inputs to the last neuron is increased by 2 times. But in principle, the structure does not change.
All sources are here - github.com/ZlodeiBaal/NeuronNetwork . Written in C #. OpenCV dlls are large, so after downloading you need to unzip inside the lib.rar folder. Or download the project here immediately, you don’t need to unpack anything - yadi.sk/d/lZn2ZJ_BWc4DB .
The code was written for 2 pm somewhere, so it is far from industry standards, but it seems to be clear (I wrote the article on the Habr longer, admittedly).

Sitting in the evening and suffering from the need to do something useful, but I don’t feel like it, I came across another article on neural networks and caught fire. Finally, you need to make your own neural network. The idea is commonplace: everyone loves neural networks, there are tons of open source examples. I sometimes had to use both LeNet and OpenCV networks. But I was always alarmed that their characteristics and mechanics I know only by pieces of paper. And between the knowledge of “neural networks are taught using the backpropagation method” and the understanding of how to do this, there is a huge gap. And then I decided. It's time to sit for 1-2 evenings and do it yourself, figure it out and understand.
A neural network without a puzzle that a horse without a rider. To solve a serious problem made on a knee by a neural network is to spend a lot of time on debugging and processing. Therefore, a simple task was needed. One of the simplest tasks in signal processing that can be solved purely mathematically is the problem of detecting white noise. The plus of the problem is precisely that it can be solved on a piece of paper, you can evaluate the accuracy of the resulting network in comparison with a mathematical solution. After all, not in every task it is possible to evaluate how well the neural network worked just by checking the formula.
Task
To begin, we formulate the problem. Suppose we have a sequence of N elements. In each of the elements of the sequence there is noise, with zero expectation and a single dispersion. There is a signal E, which can be in this sequence with a center from 0.5 to N-0.5. We set the signal with a Gaussian with such a dispersion that, when located in the center of the pixel, most of the energy is in the same pixel (it will be boring with a very point one). It is necessary to decide whether there is a signal in the sequence or not.
“What a synthetic task!” You say. But it is not so. This problem arises every time you work with point objects. It can be stars in the image, it can be a reflected radio (sound, optical) pulse in a time sequence, it can even be some microorganisms under a microscope, not to mention planes and satellites in a telescope.
We write a little more strictly. Let there be a sequence of signals l 0 ... I n containing normal noise with constant dispersion and zero mathematical expectation: The
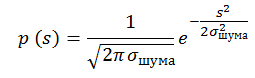
probability that a pixel contains a signal s is equal to p (s). An example of a sequence filled with normally distributed noise with dispersion 1 and expectation 0:

There is also a signal with a constant signal-to-noise ratio, SNR = E_signal / σ_noise = const. We have the right to write this when the signal size is approximately equal to the pixel size. The signal is also set by us by a Gaussian:

For simplicity, we assume that the signal σ_ = 0.25 ∙ L, where L is the pixel size. And this means that for a signal located in the center of the pixel, the pixel will contain the signal energy from - 2σ to + 2σ:

This is how the last sequence with noise looks like, on top of which a signal is superimposed with SNR = 5 centered at 4.1:

By the way, and do you know how to generate a normal distribution ?
It's funny, but many use the central limit theorem to generate it.. In this method, 6 linearly distributed values are added in the range of -0.5 to 0.5. It is believed that the resulting value is distributed normally with a dispersion of unity. But this method gives incorrect distribution tails, with large deviations. If we take exactly 6 quantities, then max = | min | = 3 = 3 * σ. Which immediately cuts off 0.2% of implementations. When generating a 100 * 100 image, such events should occur in 20 pixels, which is not so small.
There are good algorithms: The Box-Muller , Converting George Marsaglia
Habré has a good article on this topic.
All these methods are based on the mathematical transformation of the linear distribution on the interval [0; 1] into the normal distribution.
Neuron
A lot has been written about the neural network. I will try not to go into details, limiting myself only to links and main points.
A neural network consists of neurons. Nobody knows exactly how a neuron is arranged in a person, but there are many beautiful models. On a habr there were many interesting articles about neurons: 1 , 2 , etc.
In the problem, I took as a basis the simplest scheme of neurons, when a sequence of signals is fed to the input of a neuron, which is summed up and run through the activation function:

Where is the activation function:
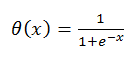

What does such a neuron do in such a model and why does it need an activation function?
A neuron compares with a certain pattern for which it is trained. And the activation function is a trigger that makes a decision on how much the pattern matches and normalizes the solution. For some reason, it often seems to me that a neuron looks like a transistor, but this is a digression:

Why not make the activation function a step? There are many reasons, but the main one, which will be discussed a little later, is a learning feature that requires differentiation of the neuron function. The above activation function has a very good differential:

Neural network
We have a network. How to solve the problem? The classic way to solve a simple problem is to create a neural network of this kind:

It has an input signal, one hidden layer (where each neuron is connected to all input elements) and an output neuron. Training such a network is, in fact, setting up all the coefficients w and v.
We will do almost this, but after optimizing for the task. Why train every neuron of the hidden layer for every pixel of the input image? The maximum signal takes three pixels, and most likely even two. Therefore, we connect each neuron of the hidden layer with only three neighboring pixels:

With this configuration, the neuron is trained in the vicinity of the image, starting to work as a local detector. An array of trained elements for the hidden layer (1..N) will look like:
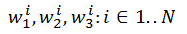
As an experiment, I introduced two output neurons, but as it turned out later, this did not make much sense.
This type of neural network is one of the oldest used in the work. Recently, more and more people are using convolutional networks. About convolution networks already repeatedly wrote on a habr: 1 , 2 .
A convolutional network is a network that searches and remembers existing patterns that are universal for the entire image. Usually, to demonstrate what a neural network is, they draw an image like this:

But when you start trying to code it, the brain goes into a stupor of "how can this be applied to reality." But in reality, the above example of a neural network is translated into a convolutional network with just one action. To do this, when learning, it is enough to assume that the elements w 1 1 , ..., w 1 N are not different elements, but the same element w 1 . Then, as a result of training the hidden layer, only three elements w 1 , w 2 , w 3 will be found , which are a convolution.
True, as it turned out, one convolution is not enough to solve the problem, you need to enter a second one, but this is easy to do by increasing the number of elements in the hidden layer to 1..2N, while the elements 1..N train the first convolution, and the elements N .. 2N is the second.
Training
A neural network is simple to draw, but not so simple to train. When you do this for the first time, the brain turns a little. But, fortunately, there are two very good articles in Runet, after which everything becomes clear as a day: 1 , 2
The first illustrates very well the logic and order of learning, the second is a well-described mathematical essence: where does what comes from formulas, how does the neural network get initialized how to correctly calculate and apply the coefficients.
In general, the method of back propagation of the error is as follows: apply a known signal to the input, distribute it to the output neurons, compare with the desired result. If there is a mismatch, then the error value is multiplied by the weight of the connection and passed to all neurons on the last layer. When all neurons know their error, then shift their learning coefficients so that the error decreases.
If anything, then you should not be afraid of learning. For example, the error definition is made in one line like this:
public void ThetaForNode(Neuron t1, Neuron t2, int myname)
{
//Величина ошибки считается как обратная проекция нейрона
BPThetta = t1.mass[myname] * t1.BPThetta + t2.mass[myname] * t2.BPThetta;
}
And the correction of weights like this:
public void CorrectWeight(double Speed, ref double[] massOut)
{
for (int i = 0; i < mass.Length; i++)
{
//Старый вес + скорость*ошибку*вход*результат*(1-результат)
massOut[i] = massOut[i] + Speed * BPThetta * input[i] * RESULT * (1 - RESULT);
}
}
Result
To begin with, as promised, we calculate "what should be." Suppose we have an SNR (signal to noise) ratio of 3. In this case, the signal is 3 times higher than the noise variance. Let's draw the probability that the signal in the pixel takes the value X:
The graph immediately shows the graphs only for the probability distribution of noise and the graph of the probability distribution of signal + noise at a point with the ratio SNR = 3. In order to make a decision on finding a signal, you need to select a certain Xs, consider all values greater than it as a signal, all values less than noise. We will draw the probability that we made a decision about false alarm and skipping an object (for the red graph this is its integral, for the blue “1-integral”):
The intersection point for such graphs is usually called the EER (Equal Error Rate). At this point, the probability of an incorrect decision is equal to the probability of losing the object.
In this problem, we have 10 input signals. How to choose an EER point for such a situation? Simple enough. The probability that a false alarm does not occur at the selected value of Xs will be equal to (the integral in the blue graph from the first figure):
Accordingly, the probability that a false alarm does not occur at 10 pixels is equal to: The
probability that at least 1 false alarm occurs is equal to 1 -P. We draw the 1-P graph and, next to it, the graph of the object skip probability (duplicate from the second graph):
Therefore, the EER point for the signal and noise at SNR = 3 is in the region of the two and EER≈0.2 in it. And what will the neural network give?
It can be seen that the neural network will be slightly worse than the problem solved on the fingers. But it is not all that bad. In mathematical consideration, we did not take into account several features (for example, the signal may not go to the center of the pixel). Without going particularly deeply, we can say that this does not significantly worsen the statistics, but it worsens.
To be honest, I was encouraged by this result. The network copes well with a purely mathematical problem.
Annex 1
Nevertheless, my main task was to create a neural network from scratch and poke a wand into it. In this section there will be a couple of funny gifs about the behavior of the network. The network turned out to be far from ideal (I think that the article will be accompanied by crushing comments by professionals, because this topic is popular on Habré), but I learned a lot of design and writing features as a result of writing and from now on I will try not to repeat it, so I'm personally pleased.
The first GIF for a regular network. The upper bar is the input signal in time. SNR = 10, the signal is clearly visible. The lower two strips are the entrance to the summation of the last neuron. It is seen that the network stabilized the image and when the signal is turned on or off, only the contrast of the inputs of the last neuron changes. It is funny that in the absence of a signal the image is almost stationary.
The second GIF is the same for the convolution network. The number of inputs to the last neuron is increased by 2 times. But in principle, the structure does not change.
Appendix 2
All sources are here - github.com/ZlodeiBaal/NeuronNetwork . Written in C #. OpenCV dlls are large, so after downloading you need to unzip inside the lib.rar folder. Or download the project here immediately, you don’t need to unpack anything - yadi.sk/d/lZn2ZJ_BWc4DB .
The code was written for 2 pm somewhere, so it is far from industry standards, but it seems to be clear (I wrote the article on the Habr longer, admittedly).
