How Bitcoin Protocol Actually Works
- Transfer
(A wonderful explanation of the principles of operation of the Bitcoin network by Michael Nielsen. A lot of text, a few pictures. About all the clumsy translation - in PM, I will correct it as soon as I find out)
Many thousands of articles were written to explain Bitcoin - online, peer-to-peer (p2p) currency . Most of these articles superficially describe the essence of the cryptographic protocol, omitting many details. Even those articles that “dig” deeper often ignore important points. My goal in this publication is to explain the main ideas that are in the Bitcoin protocol in a clear, easily accessible form. We will start with simple principles, then go to a broad theoretical understanding of how the protocol works, and then dig deeper, looking at the raw data in a Bitcoin transaction.
It is quite difficult to understand the protocol in detail. Instead, it is much easier to take Bitcoin for granted and engage in speculation on how to get rich with Bitcoin, whether Bitcoin is a bubble, whether Bitcoin can one day destroy mandatory taxation, and so on. This is all fun, but significantly limits your understanding. Understanding the details of the Bitcoin protocol opens up inaccessible prospects. In particular, this is the basis for understanding the built-in scripting language (scripting programming language) Bitcoin, which makes it possible to use Bitcoin to create new types of financial instruments, such as smart contracts ( 1 2) New financial instruments can, in turn, be used to create new markets and obtain new forms of collective human behavior.
I will describe concepts such as contracts in the following publications. This post concentrates on explaining the inside of the Bitcoin protocol. To understand me, you must be familiar with the idea of a public crypto key , and with closely related ideas about digital signatures . I also assume that you are familiar with the cryptographic hash function(changing the input data by just one bit drastically changes the hash sum, approx. per.). None of this is very difficult. The main ideas can be obtained from first-year programs in mathematics at the university or classes in computer informatics. The ideas are beautiful, so if you are not familiar with them, I recommend spending a few hours to familiarize yourself.
It may seem surprising that cryptography is the basis of Bitcoin. Isn't Bitcoin a currency, not a way to send secret messages? In fact, the problems that Bitcoin should solve mainly concern the security of transactions - to be sure that people cannot steal from each other, or impersonate each other, and so on. In the world of atoms, we achieve this security with devices such as locks, safes, signatures, and bank vaults. In the world of bits, we achieve this kind of security with cryptography. And that's why Bitcoin in the soul is a cryptographic protocol.
The strategy that I will use in my publication involves the creation of Bitcoin in stages. I will begin by explaining a very simple digital currency based on ideas that are almost obvious. We will call this currency Infocoin to distinguish it from Bitcoin. Of course, our first version of Infocoin will have many shortcomings, and therefore we will go through several iterations of Infocoin, with each new iteration we will introduce only one or two simple new ideas. After several such iterations, we will come to the complete Bitcoin protocol. We will rediscover Bitcoin!
This strategy works more slowly than if I explained the operation of the entire Bitcoin protocol in one gulp. Even if you can understand the mechanics of Bitcoin through such a volley explanation, it will be difficult to understand why Bitcoin is designed in this way. The advantage of a slow, iterative explanation is that it gives us a much clearer understanding of each element of Bitcoin.
Finally, I must mention that I am new to Bitcoin. I have been watching it since 2011 (and cryptocurrencies since the end of the 1990s), but I only really delved into the details of the Bitcoin protocol at the beginning of this year. So I will be grateful for the correction of any errors on my part. In addition, in my material I included a number of “problems for the author,” notes for myself about issues that arose during my writing. You may find them interesting, but you can also skip them completely without losing the main text.
So how can we design a digital currency?
At first glance, a digital currency seems impossible. Imagine a person — let's call her Alice — she has some digital money that she wants to spend. If Alice can use a bit string as money, how can we stop her from using the same bit string again and again, thus creating an unlimited amount of money? Or, if we can somehow solve this problem, how can we prevent falsification of such a string of bits and use it to steal from Alice?
These are just two of the many challenges that must be overcome in order to use information as money.
In the first version of Infocoin, let's find a way for Alice to use a string of bits in a (very primitive and incomplete) form of money, but in such a way that she has at least some kind of protection against fake. Suppose Alice wants to give another person, let's call him Bob, one infocoin. To do this, Alice writes the message “I, Alice, give Bob one infocoin . ” Then she signs the message in digital format using the private encryption key (crypto key), and announces the signed string of bits to the whole world.
(By the way, I use “Infocoin” with a capital letter to denote the protocol and the general concept, and “infocoin” with a capital letter to denote a specific currency. This practice is common, although not universal, in the Bitcoin world.)
Such a prototype digital currency will not really impress you! But he has some advantages. Anyone in the world (including Bob) can use Alice’s public key to verify that Alice was actually the person who signed the message “I, Alice, give Bob one infocoin . ” No one else could create this string of bits, which means Alice cannot turn around and say: “No, I didn’t mean at all that I wanted to give Bob one infocoin”. Thus, the protocol establishes that Alice really intends to give Bob one infocoin. The same fact - no one could compose such a signed message - gives Alice some limited protection against fake. Of course, after Alice published her message, there is the possibility of duplicating her message by other people, so in a sense fake is possible. But this is not possible from scratch. These two features — Alice’s determination of intent and limited counterfeit protection — are truly remarkable features of this protocol.
I (completely) did not say that, in fact, there is digital money. I explain: this is just the message itself, that is, a sequence of bits, or rather, a digitally signed message: "I, Alice, give Bob one infocoin". In the future, protocols will be similar in that all of our forms of digital money will simply be more meaningful messages.
Проблема с первой версией Инфокоин в том, что Алиса может продолжать посылать Бобу то же подписанное сообщение снова и снова. Предположим, Боб получает десять копий подписанного сообщения «Я, Алиса, даю Бобу один инфокоин». Означает ли это, что Алиса послала Бобу десять различных инфокоинов? Было ли ее послание случайно дублированным? Возможно, она пыталась обмануть Боба, притворяясь, что она дала ему десять различных ифнокоинов, в то время как сообщение лишь доказывает всему миру, что она намерена передать один инфокоин.
Чего бы нам хотелось, так это найти способ сделать инфокоины уникальными. Они нуждаются в лейбле или серийном номере. Алиса подпишет сообщение «Я, Алиса, даю Бобу один инфокоин, с серийным номером 8740348». Потом, позже, Алиса может подписать сообщение “I, Alice, give Bob one infocoin, with serial number 8770431,” and Bob (and everyone else) will know that another infocoin has been transmitted.
For this scheme to work, we need a reliable source of serial numbers for infocoins. One way to create such a source is to open a bank. This bank will provide serial numbers for infocoins, track who has which infocoins, and verify that transactions are truly legitimate.
More specifically, let's assume that Alice comes to the bank and says: “I want to withdraw one infocoin from my account”. The bank reduces its account balance by one infocoin, and assigns it a new, never-used serial number, say 1234567. Then, when Alice wants to give her infocoin to Bob, she signs the message “I, Alice, give Bob one infocoin with serial number 1234567 " . But Bob is not just taking infocoin. Instead, he makes contact with the bank and verifies that: (a) the infocoin with this serial number belongs to Alice; and (b) Alice has not yet spent this infocoin. If the conditions are correct, then Bob informs the bank that he wants to accept this infocoin, and the bank updates his records to indicate that the infocoin with this serial number is currently at Bob's disposal and no longer belongs to Alice.
This last decision looks quite promising. However, it turns out that we can do something much more ambitious. We can completely exclude the bank from the protocol. This significantly changes the nature of the currency. This means that there is no longer a single organization responsible for the currency. And if you imagine the enormous power in the hands of the central bank - control over the money supply - this is a pretty serious change.
The idea is for everyone (collectively) to be a bank. In particular, we assume that all Infocoin users keep a complete record of who owns the Infocoins. You can imagine this as an open general ledger with all of the Infocoin transactions. We will call this book “blockchain” (blockchain), that's what Bitcoin calls the public record of all transactions.
Now suppose Alice wants to pass the infocoin to Bob. She signs the message “I, Alice, give Bob one infocoin with serial number 1234567” , and sends the signed message to Bob. Bob can use his copy of the blockchain to check if the infocoin really belongs to Alice. If this is verified, then he simultaneously sends Alice a message and a message on the acceptance of the transaction across the network and everyone updates their copies of the block chain.
We still have the problem of “where does the serial number come from”, but it turns out to be quite easy to solve, and therefore I will postpone it for later, when we discuss Bitcoin. A more complex problem is that this protocol allows Alice to cheat through double spending her infocoins. She sends the signed message “I, Alice, give Bob one infocoin with serial number 1234567” to Bob, and the message “I, Alice, give Charlie one infocoin, with [the same] serial number 1234567”Charley. Both Bob and Charlie use their copy of the blockchain to verify that the infocoin belongs to Alice. Provided that they do this check at the same time (before they had the opportunity to hear from each other), both will see that, yes, the chain of blocks shows Alice's coin ownership. So, they both accept the transfer and also broadcast information about the acceptance of the transaction together. Now we have a problem. How should other people update their blockchain? It may not be so easy to find a way to get a consistent shared transaction book. And even if everyone can agree to update their blockchain on an ongoing basis, there is another problem that Bob or Charlie might be cheated on.
At first glance, re-spending looks difficult for Alice to implement. In the end, if Alice sends the message first to Bob, then Bob can check the message and tell everyone else on the network (including Charlie) to update their block chains. Once this happened, Charlie could no longer be fooled by Alice. So, most likely, only in a short period of time Alice can make repeated expenditures. However, obviously, any such period of time is undesirable. Even worse, there are methods by which Alice can make this period longer. She can, for example, use network traffic analysis to find the time when Bob and Charlie have many communication delays. Or perhaps she can do something to consciously disrupt their connection. If she can slow the connection even a little,
How can we solve the double cost problem? The obvious solution is that when Alice sends Bob one infocoin, Bob should not try to verify the deal alone. Most likely, he should broadcast a possible transaction to all users of the Infocoin network, and ask them to help him determine whether the transaction is legitimate. If they all decide that the deal is in order, then Bob can accept this infocoin and everyone will update their block chains. This type of protocol can help prevent the double-cost problem, because if Alice tries to spend her info-box with Bob and Charlie, other people on the network will notice, and network users will tell Bob and Charlie that there is a problem with the transaction, and the transaction should not be implemented.
In more detail, let's assume that Alice wants to give Bob one infocoin. As before, she signs the message “I, Alice, give Bob one infocoin with serial number 1234567”, and gives a signed message to Bob. Just like before, Bob does a health check using his copy of the blockchain to check if the coin really belongs to Alice. But at that moment the protocol is changed. Bob doesn't just go ahead and accept the deal. Instead, it sends Alice a message to the entire network. Other network members check if Alice has this infocoin. If so, they send the message "Yes, Alice owns the infocoin 1234567, now it can be transferred to Bob." As soon as a sufficient number of people spread this message on the network, everyone will update their blockchain, which will show that infocoin 1234567 is now owned by Bob, and the transaction is completed.
This protocol has many inaccurate elements at present. For example, what does it mean to say “enough people should broadcast this message”? What does “enough” mean? This cannot mean everyone on the network, since we do not know a priori who is on the Infocoin network. For the same reason, this cannot mean some fixed share of users on the network. We will not try to figure this out right now. Instead, in the next section I will point out serious problems in the approach that we described. By paying attention to this problem, we will have a pleasant side effect of creating the ideas above more understandable.
Suppose Alice wants to spend again in the protocol I just described. She can do this by taking control of the Infocoin network. Let's assume that it uses an automated system to configure a large number of individual identities (users), say, a billion, on the Infocoin network. As before, she is trying to pay the same infocoin to Bob and Charlie twice. But when Bob and Charlie ask the network to verify the transactions, Alice's additional users will fill up the network, announcing to Bob that they confirmed his transaction, and Charlie that they confirmed his transaction by deceiving one or both at the same time, accepting such a transaction.
There is a way to avoid this problem by using an idea known as proof-of-work. The idea is paradoxical and involves a combination of two other ideas: (1) (artificially) making confirmation of transactions costly for network users in the form of computer calculations; and (2) reward them for helping verify transactions. The reward is used so that people on the network try to help verify transactions, despite the need to spend computing power on this process. The benefit of verifying transactions is cost-effective, helping to avoid dependence on the number of identities (network users) controlled by someone. Thus, only the total computing power can put pressure on the test. As we will see, using some clever design, we can do so
Here is the essence of proof of proper operation. But in order to truly understand, we must look at the details.
Suppose Alice broadcasts the news “I, Alice, give Bob one infocoin with serial number 1234567” .
Upon hearing this message, everyone adds it to the queue of pending transactions: they are heard, but have not yet been approved by the network. For example, another network user named David may have the following queue of pending transactions:
I, Tom, give Sue one info-code, with serial number 1201174.
I, Sydney, give Cynthia one info-code, with serial number 1295618.
I, Alice, give Bob one infocoin with serial number 1234567.
David checks his copy of the blockchain and sees that every trade is good. He would like to help by sending news about the validity of transactions for the entire network.
Nevertheless, before doing this, as part of the verification protocol, David needs to solve a difficult computational problem - proof of correct operation. Without solving this problem, the rest of the network will not accept its verification of transactions.
What problem does David need to solve? To explain this, let h be a fixed hash function known to everyone on the network - it is built into the protocol. Bitcoin uses the famous SHA-256 hash functionbut any cryptographically secure hash function will do. Let's give David's queue of unfinished deals L label, so it’s more convenient for us to refer. Suppose David adds the number x (the so-called one-time number) and computes the hash sum from the combination. For example, if we use L = “Hello, world!” (Obviously this is not a list of operations, just a line is used to illustrate) and a one-time x = 0, then (we get the output in hexadecimal format)
h (“Hello, world! 0 ") = 1312af178c253f84028d480a6adc1e25e81caa44c749ec81976192e2ec934c64
The task that David must solve is proof of correct operationIs to find a prime number x so that when we add x to L and the result of the hash of the combination starts with a series of zeros. A task can be made more or less difficult by changing the number of zeros needed to solve this problem. A relatively simple proof of the correctness of the task can require only three or four zeros at the beginning of the hash, while a more difficult proof of the correctness of the task can require a much larger number of zeros, say 15 consecutive zeros. In any case, the above attempt to find a suitable one-time number with x = 0 failed, because the result does not start from scratch. Let's try x = 1 ,. Also does not work:
h ("Hello, world! 1") = e9afc424b79e4f6ab42d99c81156d3a17228d6e1eef4139be78e948a9332a7d8
We can continue to look for different values for x = 2,3,4 .... finally, with x = 4250 we get:
h ("Hello, world! 4250") = 0000c3af42fc31103f1fdc0151fa747ff87349a4714df7cc52ea464e12dcd4e9
This number gives us a string of four zeros at the beginning of the hash output . This will be enough to solve the simple task of "proof of work", but not enough to solve the more difficult problem of "proof of work".
There is a thing that makes this task difficult to solve. The result of the cryptographic hash function behaves like random numbers: change at least one bit in the source data and the result will radically differ so much that it is impossible to predict. So, if we want to have a hash value with 10 zeros at the beginning, then David will need to sort through, on average, different x values before he finds a suitable prime number. This is a rather complicated task requiring a lot of computing power.
different x values before he finds a suitable prime number. This is a rather complicated task requiring a lot of computing power.
It is possible to make this task more or less difficult to solve through more or less number of zeros at the exit from the hash function. In fact, the Bitcoin protocol gains a fairly good level of control over the difficulty of the task, using a slight variation of the proof-of-work puzzle described above. Instead of requiring zeros, Bitcoin, as proof of proper operation, requires that the hash of the header of the transaction block be less than or equal to the number known as the target . This goal is automatically adjusted so that the Bitcoin block takes, on average, about ten minutes for authorization.
(In practice, there is significant chance in how much time it takes to approve a block - sometimes a new block is approved in just a minute or two, and in other cases it can take 20 minutes or even more. This changes directly in the Bitcoin protocol, so the time for verification, it usually reaches a maximum of about ten minutes. Instead of solving a single problem, we may require solving several problems; using a carefully designed software design, we can significantly reduce the variance in time for checking the block s Christmas tree.)
Ok, let's assume that David was lucky and he found the right number x. Hurrah! (He will receive a reward for finding the number, as will be described below). It translates the block of operations, which it claims, into the network along with the value of x. Other members of the Infocoin network can verify that x is a solution to proving the correctness of the task. And then they must update their block chains to include the new block of operations in the chain.
In order for the idea of proof of correct operation to have a chance of success, network users need an incentive to help them verify transactions. Without such an incentive, they have no reason to waste valuable computing power just to help verify other people's operations. And if network users are not ready to spend this power, then the whole system will not work. The solution to this problem is to reward people who help verify transactions. In particular, suppose we reward those who have successfully verified a block of transactions by crediting them with a certain amount of infocoins. The reward for infocoin is so great that it will give them an incentive to participate in the test.
In the Bitcoin protocol, this confirmation process is called mining. For each block of transactions verified, a successful miner receives a reward in bitcoins. Initially, this award was set at 50 bitcoins. But for every 210 thousand checked blocks (approximately once every four years), the reward is halved. This happened only once. To date, the reward for mining the block is 25 bitcoins. This half-rate cut will continue every four years until the year 2140. At that point, the mining reward will drop below 10 ^ -8 bitcoins per block. 10 ^ -8 bitcoins, in fact, is the smallest unit of Bitcoin, and is known as Satoshi . Thus, in 2140, the total supply of bitcoins will cease to increase. However, this will not eliminate the incentive to continue checking transactions. Bitcoin also makes it possible to allocate a certain amount in the transaction as a transaction fee, which will go to the miner, which helps to accept transactions. In the early days of Bitcoin, the transaction fee was zero, but with the popularity of Bitcoin, transaction fees gradually increased, and are now an additional addition to the reward of 25 Bitcoins for the mining block.
You can think of proof of work as a competition who accepts transactions faster. Each entry to the competition costs a bit of processing power. The chance that a miner wins the competition is (roughly speaking, and with some reservations) equal to the total processing power that they control. So, for example, if a miner controls one percent of all the processing power used to verify transactions in Bitcoin, then it has about one percent chance of winning. That is, provided that a lot of computing power is involved in the competition, a dishonest miner will most likely have a relatively small chance of distorting the verification process, unless he spends a huge amount of computing resources.
Of course, while this inspires inspiration, the dishonest side has only a relatively small chance to ruin the block chain, but this is not enough to inspire confidence in the currency. In particular, we have not yet fully resolved the issue of re-spending.
I will analyze double costs soon. Before doing this, I want to fill out an important detail in the Infocoin description. It would be ideal to coordinate the order in the Infocoin network in which the transactions took place. If we do not have such an order, then at any moment it may become unclear who owns which infocoins. To solve this, we will require that new blocks always include a pointer to the previous block approved in the chain, in addition to the list of transactions in the block. (The pointer is actually just a hash of the previous block). So, we have a block chain - it’s just a direct chain of transaction blocks, one after another, where each block contains a pointer to the immediately previous block:

Sometimes, a plug appears in a chain of blocks. This can happen, for example, if by chance two miners checked the block of operations at the same time - and both broadcast their newly approved block to the network, and some people will update their block chain in one direction, and others will update in the other direction:
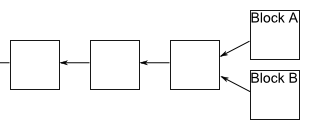
It would seem that this causes a problem which we are trying to avoid - it is no longer clear in what order the transactions occurred, and this does not clarify who owns which infocoins. Fortunately, there is a simple idea that can be used to remove any plugs. The rule is this: if a plug suddenly happens, people on the network track both branches. But at any given time, miners only work on continuing the branching in which a copy of the block chain is longer.
Suppose we have a fork in which some miners get block A first and some miners get block B. Those miners who get block A first will continue to work along this branch, while other miners will go along with branch B. Suppose that miners working on branch B successfully mined a block:
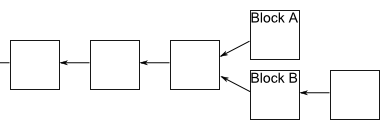
After everyone receives the news that this has happened, miners working on branch A will notice that branch B is now longer and will switch to work on this branch. That's all! Immediately, the work on branch A will stop, and everyone will work on the same linear chain, and block A can be ignored. Of course, any unconfirmed transactions included in block A will still be waiting for decisions in the queues of miners working on branch B, and subsequently all transactions will be confirmed. In addition, it may turn out that miners working on branch A will expand it earlier. In this case, work on branch B stops quickly, and again we have one linear chain.
Regardless of the outcome, this process ensures that the block chain has a time-aligned ordering of transaction blocks. It is accepted in Bitcoin that a transaction is not considered confirmed before: (1) it is part of a block in a long branch, and (2) at least 5 blocks followed it in the longest branch. In this case, we say that the transaction has “6 confirmations”. This allows the network time to arrive at a consistent ordering of blocks. We will also use this strategy for infocoin.
We sorted out the streamlining, let's get back to thinking about what happens if a dishonest user tries to spend twice. Suppose Alice tries to spend an infocoin twice with Bob and Charlie. One of the possible approaches for her is to try to independently check the block, which includes both transactions. Assuming that she has one percent of the total computing power, she can get lucky, and she confirms the block by solving the mathematical problem of proof-of-work. Unfortunately, for Alice, the re-payment will be immediately noticed by other people on the Ifnokoin network and rejected, despite solving the problem with proof of correct operation. So we don’t need to worry.
A more serious problem arises if she broadcasts separately two transactions in which she conducts the same infocoin with Bob and Charlie, respectively. It can, for example, broadcast one transaction to one group of miners, and another transaction to another, hoping to obtain approval of transactions in this way. Fortunately, in this case, as we have seen, the network will finally confirm only one of these transactions, but not both. So, for example, Bob’s deal can ultimately be confirmed, in which case Bob can be calm. Meanwhile, Charlie will see that his deal has not been confirmed, and he will refuse Alice’s offer. So there is no problem. In fact, knowing that this will happen, there is no particular reason for Alice to try this.
There is another important option for double spending if Alice = Bob, i.e. Alice is trying to pay Charlie's coin, which she also “spends” to herself (that is, giving herself back). It looks like it’s easy to notice and deal with it, but at the same time, of course, it’s easy to set up several users connected to the same person or organization on the network, so this possibility must be taken into account. In this case, Alice’s strategy is to wait until Charlie accepts the infocoin, which will happen after the transaction has been confirmed 6 times in the longest chain. She will try to fork the chain before a deal with Charlie, adding a block that includes a payment transaction to herself:

Unfortunately, it is very difficult for Alice to catch up with the longer branch. Other miners do not want to help her, as they will work on a longer branch. And until Alice can solve the proof of correct operation, at least as fast as everyone else on the network together - roughly speaking, this means that controlling more than fifty percent of the processing power - she will simply lag further and further behind. Of course she might be lucky. We can, for example, imagine a scenario in which Alice controls one percent of the processing power, but luck happens and she finds six additional blocks in a row before the rest of the network finds any new block. In this case, she could get ahead, and gain control over the chain of blocks. But this particular event will happen with a probability of 1 / (100 ^ 6) = 10 ^ -12. A more general analysis in this direction shows that Alice’s probability of catching up with the longer branching of the blocks is infinitely small if she is not able to solve the proof of the correct operation at a speed close to all other miners combined.
Of course, this is not a thorough safety analysis, showing Alice's inability to make repeated expenses. This is just an unofficial argument of credibility. The original text representing Bitcoin, in fact, does not contain a thorough security analysis, only informal arguments on the points that I presented. The community that is interested in security is still analyzing Bitcoin and trying to understand possible vulnerabilities. You can see some of these studies here , and I will mention a few problems in “Problems for the author” below (see in the original test). At the moment, I think it's fair to say that the jury still does not know how secure Bitcoin is.
Ideas of proof of proper operation and mining raise many questions. What reward is needed to convince people to mine? How will changes in infocoin emissions affect Ifnocoin's economy? Will mining Infocoin ultimately be concentrated in the hands of a few, or many? If there are only a few miners, will this jeopardize system security? Presumably, the cost of transactions will balance over time - will this not lead to an undesirable source of friction, and will not make small transactions less desirable? These are all big questions that are beyond the scope of this article. I can return to these issues (in the context of Bitcoin) in future publications. Currently, we will focus on understanding how the Bitcoin protocol works.
Let's move away from Infocoin and describe the actual Bitcoin protocol. There are a few new ideas here, but with one exception (see below) that they are basically obvious modifications of Infocoin.
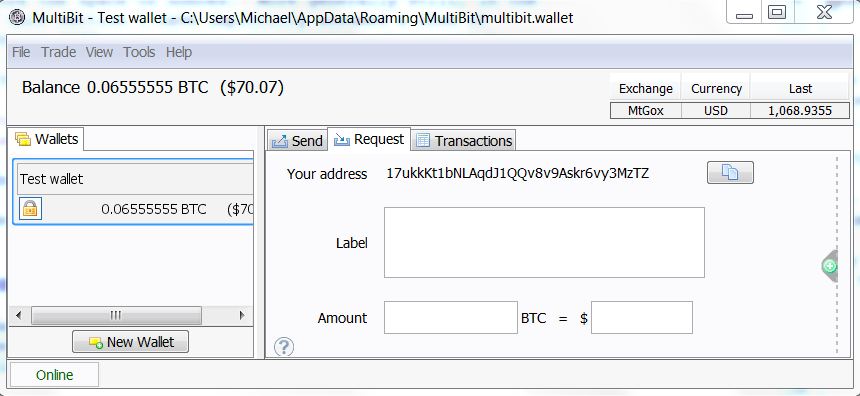
In order to use Bitcoin in practice, we first install the wallet program on your computer. To give you an idea of what this means, here is a screenshot from a wallet program called Multbit. You can see the balance of bitcoins on the left - 0.06555555 bitcoin, or about $ 70 at the exchange rate for the day I took this screenshot - and on the right are two recent transactions that form 0.06555555 bitcoins:

Suppose you are a merchant who created an online store and decided to allow people to pay for your goods using Bitcoin. The first thing you do is generate a Bitcoin address in the program. In response, he will generate a public / private key pair, and then a public key hash to form his Bitcoin address:
Then you send the Bitcoin address to the person who wants to buy from you. You can do this by email, or even put the address publicly on a web page. This is safe, because the address is just a hash value of your public key, which can be safely known in the world anyway. (I will return later to the question of why the Bitcoin address is a hash, and not just a public key.)
The person who will pay you generates the transaction. Let's take a look at the data from a real transaction transmitting 0.31900000 bitcoins. The following shows almost raw data. They are changed in three ways: (1) the data was converted from serial to parallel (deserialized); (2) line numbers that have been added for ease of use; and (3) I shortened the various hashes and public keys by simply displaying the first six hexadecimal digits of each, when in fact they are much longer. Here are the data:
Let's go line by line.
Line 1 contains the hash of the remainder of the transaction, 7c4025 ..., expressed in hexadecimal. This is used as a transaction identifier.
Line 2 tells us that this is a deal in version 1 of the Bitcoin protocol.
Lines 3 and 4 tell us that the transaction has one input and one output, respectively. I will talk below about transactions with a large number of inputs and conclusions, and why this is useful.
Line 5 contains the value of lock_time, which can be used to control when the transaction is completed. For most transactions, Bitcoin today lock_time is set to 0, which means that the transaction is completed immediately.
Line 6 tells us the size (in bytes) of the transaction. Please note that this is not a cash transfer! About it further.
Lines 7 through 11 define the introductory bitcoins for the operation. In particular, lines 8 through 10 tell us that the input should be taken from the output from the previous transaction with the corresponding hash amount, which is expressed in hexadecimal format as 2007ae .... .n = 0 tells us that this will be the first conclusion from that transaction; we will see in the near future how several conclusions (and inputs) in a transaction work, so don’t worry too much about it now. Line 11 contains the signature of the person transferring the money - 304502 ..., then a space, and then the corresponding public key -04b2d .... Again in hexadecimal format.
The only thing that should be noted about the input is the lack of an exact indication of how many bitcoins from the previous transaction should be spent in this transaction. In fact, all bitcoins from n = 0 of the output of the previous transaction were spent. So, for example, if the n = 0th output from the previous transaction was 2 bitcoins, then 2 bitcoins will be spent in this transaction. This seems like an uncomfortable restriction - it’s the same as trying to buy bread with a $ 20 bill, and is not able to break it into small banknotes. The solution, of course, must have a mechanism for getting change. This can be done using transactions with several inputs and outputs, which we will discuss in the next section.
Lines 12 through 14 determine the withdrawal of bitcoins from the transaction. In particular, line 13 tells us the value of the output: 0.319 bitcoins. Line 14 is a rather complicated process. It is important to note that the value of a7db6f ... is the Bitcoin address of the intended recipient (written in hexadecimal format). Actually, line 14 is nothing more than a display of the Bitcoin scripting language. I am not going to describe this programming language in detail in this note, the main thing for us to understand is that a7db6f ... is only a Bitcoin address.
By the way, now you can see how Bitcoin is calling for a problem that I “tucked up my sleeve” in the last chapter: where do the Bitcoin serial numbers come from? In fact, the role of the serial number is played by the hash sum of transactions. In the transaction above, for example, the recipient receives 0.319 bitcoins that come from the first output of the previous operation with the hash sum 2007ae ... (line 9). If you go and look at the block chain for this transaction, you will see that its output comes from an even earlier transaction. Etc.
There are two smart things about using transaction hash amounts instead of serial numbers. Firstly, in Bitcoin there really are no separate, permanent (virtual) “coins”. There is simply a long series of transactions in a chain of blocks. It is a smart idea to understand that you do not need coins, and you can just get by with a book of deals. Secondly, when working in this way we remove the need for any central authority that issues serial numbers. Instead, serial numbers can be generated automatically, only by hashing the transaction.
In fact, you can continue to follow the chain of transactions further into the past. Ultimately, this process should be completed. This can happen in two ways. The first opportunity will arise when you come to the very first Bitcoin transaction contained in the so-called Genesis block . This is a special transaction that has no inputs, but only a conclusion in 50 bitcoins. In other words, this transaction sets the initial money supply. The initial block is accessed separately by clients (programs) of the Bitcoin network. And I will not go into details now, although this is very similar to the deal described above. You can see the serialized to parallel source data here .
The second possibility will be, when you follow the chain of transactions back in time, then in the end you will arrive at the so-called basic transaction (coinbase transaction). With the exception of the Start block, each block of operations in a block chain begins with a special underlying transaction. This deal is an award to the miner who will check this block of operations. It uses a similar but not identical transaction format presented above. I will not go into details on the format, and if you want to see an example, see here . You can read a little more about basic deals here.. In some ways, I was not accurate from the above, namely that it is specifically signed with a digital signature on line 11. Obviously, the payer must sign the entire transaction (except for the hash of the transaction that is generated later). Currently, this is not the case - some parts of the transaction are omitted. This makes some parts of the transaction changeable , i.e. they can be changed later. However, this plasticity is not included in the amount payable by senders and recipients, which cannot be changed later. I must admit, I did not fit into the details. As I understand it, this plasticity is under discussion in the Bitcoin developer community, and efforts are being made to reduce or eliminate this plasticity.
In the last section, I described how a deal with one input and one output works. In practice, it is often very convenient to create a Bitcoin transaction with multiple inputs or multiple outputs. I will talk later about why this might be useful. But first, let's take a look at the actual transaction data :
Let's go line by line. This is very similar to a transaction with one input and one output, so I will do it pretty quickly.
Line 1 contains the hash of the rest of the transaction. This is used as a transaction identifier.
Line 2 tells us that this is a transaction of version 1 of the Bitcoin protocol.
Lines 3 and 4 tell us that the transaction has three inputs and two outputs, respectively.
Line 5 contains lock_time. As with one input and one output, the value is 0, which means that the transaction is completed immediately.
Line 6 tells us the size of the transaction in bytes.
Lines 7 through 19 define a list of entries for the transaction. Each corresponds to a conclusion from a previous Bitcoin transaction.
The first entry is defined in lines 8 through 11.
In particular, lines 8 through 10 tell us that the input should be taken from the n = 0th output from the transaction with a hash value of 3beabc .... Line 11 contains a signature, then a space, and then the public key of the sender of bitcoin.
Lines 12 through 15 define the second input in a format similar to lines 8 through 11. And lines 16 through 19 define the third input.
Lines 20 through 24 define a list containing two conclusions from the transaction.
The first output is defined on lines 21 and 22. Line 21 tells us the output value of 0.01068000 bitcoins. As before, line 22 is an expression of the Bitcoin scripting language. The main thing to pay attention to here is the line e8c30622 ... is Bitcoin address of the intended recipient of funds.
The second conclusion is defined in lines 23 and 24 in a form similar to the first conclusion.
One obvious oddity in this description is that although each output has an indication of the amount in bitcoin associated with it, this is not in the inputs. Of course, the values of the corresponding inputs can be found by referring to the corresponding conclusions in previous transactions. In the standard Bitcoin operation, the sum of all inputs in a transaction must be at least as much as the sum of all conclusions. (The only exceptions to this principle are the Initial block and basic transactions (coinbase), both form a new offer on the Bitcoin network.) If there are more inputs than outputs, then the excess is used as a transaction fee. This is paid to the miner for a successfully verified block in which the current transaction is included.
That's all about transactions with numerous inputs and outputs! They are a fairly simple transaction variation with one input and one output.
One good use of such transactions is the idea of surrender. Suppose, for example, that I want to send you 0.15 bitcoins. I can do this by sending you money from a previous transaction in which I received 0.2 bitcoins. Of course, I do not want to send you all 0.2 bitcoins. The solution will send you 0.15 bitcoins, and send 0.05 bitcoins to your Bitcoin address, which belongs to me. These 0.05 bitcoins are surrender. This is somewhat different from the process of receiving change in a store, because change in this case is a payment to oneself. But the general idea is similar.
This concludes the basic description of the basic ideas that lie in Bitcoin technology. Of course, I omitted many details - we did not do a technical description. But I described the basic ideas for the most common cases of using Bitcoin.
Although the rules of Bitcoin are simple and easy to understand, this does not mean that it is easy to understand all the consequences of these rules. There is much more to say about Bitcoin, and I will explore some of these issues in the future.
I will conclude my post by addressing a few controversial points.
How anonymous is Bitcoin? Many people claim that Bitcoin can be used anonymously. This statement has led to the formation of markets such as the Silk Road) and various successors who specialize in illegal goods. Meanwhile, the claim that Bitcoin is anonymous is a myth. The blockchain is public and open, which means an opportunity for everyone to see any Bitcoin transaction ever. Although Bitcoin addresses are not immediately associated with real people, computer scientists have done a great job figuring out how to de-anonymize"Anonymous" social networks. A block chain is an ideal target for these methods. I will be very surprised if the vast majority of Bitcoin users are not identified with a relatively high degree of confidence and ease in the near future. This confidence will not be high enough to achieve a guilty plea, but high enough to identify likely goals. In addition, identification will be retrospective, which means that those who bought drugs on the Silk Road market in 2011 will still be able to identify themselves based on the block chain, say, in 2020. These de-anonymization methods are well known to scientists, and, presumably, to the National Security Agency (USA). I would not be surprised if the NSA and other institutions have already recognized many users. Paradoxically that Bitcoin is often touted as anonymous. This is not true. On the contrary, Bitcoin is perhaps the most open and transparent financial instrument that the world has not yet seen.
Can you get rich with Bitcoin? Well, maybe. Tim O'Reilly once said: “Money is like gas in a car - you need to pay attention or you will end up on the side of the road; but a well-lived life is not a tour of the gas station! »A lot of interest in Bitcoin comes from people whose life position is aimed at finding a really big gas station. I have to admit, I find it puzzling. In my opinion, it is much more interesting and pleasant to think of Bitcoin and other cryptocurrencies as the path to new forms of collective behavior. It is intellectually fascinating, offers wonderful opportunities for creativity, is socially valuable, and you can also put money in a bank. But if money in the bank is your main task, then I believe that other strategies have a much greater chance of success.
I omitted the details: although this post described the main ideas behind Bitcoin, there are many details that I did not mention. Here, for example, is the size preservation feature that is used by the protocol, based on a data structuring model known as the Merkle Tree . This is a detail, but a great detail, and it’s worth knowing more if data structures are your thing. You can download and explore the original Bitcoin pages . Secondly, I have already talked a bit about the Bitcoin network - questions such as how the network deals with denial of service attack, how the nodes join and leave the network, etc. This is a fascinating topic, but it also requires a lot of detail, so I omitted that. You can learn more about this at some of the links above.
Scripting language Bitcoin: In this article I explained Bitcoin as a form of digital online money. But this is only a small part of a much larger and more interesting story. As we have already seen, each Bitcoin transaction is associated with a script in a programming language Bitcoin. The scenarios that we saw in this article describe simple operations like “Alice gave Bob 10 Bitcoins . ” But the scripting language can also be used to express much more complex transactions. In other words, Bitcoin is programmable money.. In later publications, I will explain the scripting system, and how you can use Bitcoin scripts as a platform for experimenting with all kinds of amazing financial instruments.
Translation: Andrey Dubetskiy, Igor Korsakov
Many thousands of articles were written to explain Bitcoin - online, peer-to-peer (p2p) currency . Most of these articles superficially describe the essence of the cryptographic protocol, omitting many details. Even those articles that “dig” deeper often ignore important points. My goal in this publication is to explain the main ideas that are in the Bitcoin protocol in a clear, easily accessible form. We will start with simple principles, then go to a broad theoretical understanding of how the protocol works, and then dig deeper, looking at the raw data in a Bitcoin transaction.
It is quite difficult to understand the protocol in detail. Instead, it is much easier to take Bitcoin for granted and engage in speculation on how to get rich with Bitcoin, whether Bitcoin is a bubble, whether Bitcoin can one day destroy mandatory taxation, and so on. This is all fun, but significantly limits your understanding. Understanding the details of the Bitcoin protocol opens up inaccessible prospects. In particular, this is the basis for understanding the built-in scripting language (scripting programming language) Bitcoin, which makes it possible to use Bitcoin to create new types of financial instruments, such as smart contracts ( 1 2) New financial instruments can, in turn, be used to create new markets and obtain new forms of collective human behavior.
I will describe concepts such as contracts in the following publications. This post concentrates on explaining the inside of the Bitcoin protocol. To understand me, you must be familiar with the idea of a public crypto key , and with closely related ideas about digital signatures . I also assume that you are familiar with the cryptographic hash function(changing the input data by just one bit drastically changes the hash sum, approx. per.). None of this is very difficult. The main ideas can be obtained from first-year programs in mathematics at the university or classes in computer informatics. The ideas are beautiful, so if you are not familiar with them, I recommend spending a few hours to familiarize yourself.
It may seem surprising that cryptography is the basis of Bitcoin. Isn't Bitcoin a currency, not a way to send secret messages? In fact, the problems that Bitcoin should solve mainly concern the security of transactions - to be sure that people cannot steal from each other, or impersonate each other, and so on. In the world of atoms, we achieve this security with devices such as locks, safes, signatures, and bank vaults. In the world of bits, we achieve this kind of security with cryptography. And that's why Bitcoin in the soul is a cryptographic protocol.
The strategy that I will use in my publication involves the creation of Bitcoin in stages. I will begin by explaining a very simple digital currency based on ideas that are almost obvious. We will call this currency Infocoin to distinguish it from Bitcoin. Of course, our first version of Infocoin will have many shortcomings, and therefore we will go through several iterations of Infocoin, with each new iteration we will introduce only one or two simple new ideas. After several such iterations, we will come to the complete Bitcoin protocol. We will rediscover Bitcoin!
This strategy works more slowly than if I explained the operation of the entire Bitcoin protocol in one gulp. Even if you can understand the mechanics of Bitcoin through such a volley explanation, it will be difficult to understand why Bitcoin is designed in this way. The advantage of a slow, iterative explanation is that it gives us a much clearer understanding of each element of Bitcoin.
Finally, I must mention that I am new to Bitcoin. I have been watching it since 2011 (and cryptocurrencies since the end of the 1990s), but I only really delved into the details of the Bitcoin protocol at the beginning of this year. So I will be grateful for the correction of any errors on my part. In addition, in my material I included a number of “problems for the author,” notes for myself about issues that arose during my writing. You may find them interesting, but you can also skip them completely without losing the main text.
First steps: protocol of intent signed
So how can we design a digital currency?
At first glance, a digital currency seems impossible. Imagine a person — let's call her Alice — she has some digital money that she wants to spend. If Alice can use a bit string as money, how can we stop her from using the same bit string again and again, thus creating an unlimited amount of money? Or, if we can somehow solve this problem, how can we prevent falsification of such a string of bits and use it to steal from Alice?
These are just two of the many challenges that must be overcome in order to use information as money.
In the first version of Infocoin, let's find a way for Alice to use a string of bits in a (very primitive and incomplete) form of money, but in such a way that she has at least some kind of protection against fake. Suppose Alice wants to give another person, let's call him Bob, one infocoin. To do this, Alice writes the message “I, Alice, give Bob one infocoin . ” Then she signs the message in digital format using the private encryption key (crypto key), and announces the signed string of bits to the whole world.
(By the way, I use “Infocoin” with a capital letter to denote the protocol and the general concept, and “infocoin” with a capital letter to denote a specific currency. This practice is common, although not universal, in the Bitcoin world.)
Such a prototype digital currency will not really impress you! But he has some advantages. Anyone in the world (including Bob) can use Alice’s public key to verify that Alice was actually the person who signed the message “I, Alice, give Bob one infocoin . ” No one else could create this string of bits, which means Alice cannot turn around and say: “No, I didn’t mean at all that I wanted to give Bob one infocoin”. Thus, the protocol establishes that Alice really intends to give Bob one infocoin. The same fact - no one could compose such a signed message - gives Alice some limited protection against fake. Of course, after Alice published her message, there is the possibility of duplicating her message by other people, so in a sense fake is possible. But this is not possible from scratch. These two features — Alice’s determination of intent and limited counterfeit protection — are truly remarkable features of this protocol.
I (completely) did not say that, in fact, there is digital money. I explain: this is just the message itself, that is, a sequence of bits, or rather, a digitally signed message: "I, Alice, give Bob one infocoin". In the future, protocols will be similar in that all of our forms of digital money will simply be more meaningful messages.
Using serial numbers to identify coins
Проблема с первой версией Инфокоин в том, что Алиса может продолжать посылать Бобу то же подписанное сообщение снова и снова. Предположим, Боб получает десять копий подписанного сообщения «Я, Алиса, даю Бобу один инфокоин». Означает ли это, что Алиса послала Бобу десять различных инфокоинов? Было ли ее послание случайно дублированным? Возможно, она пыталась обмануть Боба, притворяясь, что она дала ему десять различных ифнокоинов, в то время как сообщение лишь доказывает всему миру, что она намерена передать один инфокоин.
Чего бы нам хотелось, так это найти способ сделать инфокоины уникальными. Они нуждаются в лейбле или серийном номере. Алиса подпишет сообщение «Я, Алиса, даю Бобу один инфокоин, с серийным номером 8740348». Потом, позже, Алиса может подписать сообщение “I, Alice, give Bob one infocoin, with serial number 8770431,” and Bob (and everyone else) will know that another infocoin has been transmitted.
For this scheme to work, we need a reliable source of serial numbers for infocoins. One way to create such a source is to open a bank. This bank will provide serial numbers for infocoins, track who has which infocoins, and verify that transactions are truly legitimate.
More specifically, let's assume that Alice comes to the bank and says: “I want to withdraw one infocoin from my account”. The bank reduces its account balance by one infocoin, and assigns it a new, never-used serial number, say 1234567. Then, when Alice wants to give her infocoin to Bob, she signs the message “I, Alice, give Bob one infocoin with serial number 1234567 " . But Bob is not just taking infocoin. Instead, he makes contact with the bank and verifies that: (a) the infocoin with this serial number belongs to Alice; and (b) Alice has not yet spent this infocoin. If the conditions are correct, then Bob informs the bank that he wants to accept this infocoin, and the bank updates his records to indicate that the infocoin with this serial number is currently at Bob's disposal and no longer belongs to Alice.
Create a bank together
This last decision looks quite promising. However, it turns out that we can do something much more ambitious. We can completely exclude the bank from the protocol. This significantly changes the nature of the currency. This means that there is no longer a single organization responsible for the currency. And if you imagine the enormous power in the hands of the central bank - control over the money supply - this is a pretty serious change.
The idea is for everyone (collectively) to be a bank. In particular, we assume that all Infocoin users keep a complete record of who owns the Infocoins. You can imagine this as an open general ledger with all of the Infocoin transactions. We will call this book “blockchain” (blockchain), that's what Bitcoin calls the public record of all transactions.
Now suppose Alice wants to pass the infocoin to Bob. She signs the message “I, Alice, give Bob one infocoin with serial number 1234567” , and sends the signed message to Bob. Bob can use his copy of the blockchain to check if the infocoin really belongs to Alice. If this is verified, then he simultaneously sends Alice a message and a message on the acceptance of the transaction across the network and everyone updates their copies of the block chain.
We still have the problem of “where does the serial number come from”, but it turns out to be quite easy to solve, and therefore I will postpone it for later, when we discuss Bitcoin. A more complex problem is that this protocol allows Alice to cheat through double spending her infocoins. She sends the signed message “I, Alice, give Bob one infocoin with serial number 1234567” to Bob, and the message “I, Alice, give Charlie one infocoin, with [the same] serial number 1234567”Charley. Both Bob and Charlie use their copy of the blockchain to verify that the infocoin belongs to Alice. Provided that they do this check at the same time (before they had the opportunity to hear from each other), both will see that, yes, the chain of blocks shows Alice's coin ownership. So, they both accept the transfer and also broadcast information about the acceptance of the transaction together. Now we have a problem. How should other people update their blockchain? It may not be so easy to find a way to get a consistent shared transaction book. And even if everyone can agree to update their blockchain on an ongoing basis, there is another problem that Bob or Charlie might be cheated on.
At first glance, re-spending looks difficult for Alice to implement. In the end, if Alice sends the message first to Bob, then Bob can check the message and tell everyone else on the network (including Charlie) to update their block chains. Once this happened, Charlie could no longer be fooled by Alice. So, most likely, only in a short period of time Alice can make repeated expenditures. However, obviously, any such period of time is undesirable. Even worse, there are methods by which Alice can make this period longer. She can, for example, use network traffic analysis to find the time when Bob and Charlie have many communication delays. Or perhaps she can do something to consciously disrupt their connection. If she can slow the connection even a little,
How can we solve the double cost problem? The obvious solution is that when Alice sends Bob one infocoin, Bob should not try to verify the deal alone. Most likely, he should broadcast a possible transaction to all users of the Infocoin network, and ask them to help him determine whether the transaction is legitimate. If they all decide that the deal is in order, then Bob can accept this infocoin and everyone will update their block chains. This type of protocol can help prevent the double-cost problem, because if Alice tries to spend her info-box with Bob and Charlie, other people on the network will notice, and network users will tell Bob and Charlie that there is a problem with the transaction, and the transaction should not be implemented.
In more detail, let's assume that Alice wants to give Bob one infocoin. As before, she signs the message “I, Alice, give Bob one infocoin with serial number 1234567”, and gives a signed message to Bob. Just like before, Bob does a health check using his copy of the blockchain to check if the coin really belongs to Alice. But at that moment the protocol is changed. Bob doesn't just go ahead and accept the deal. Instead, it sends Alice a message to the entire network. Other network members check if Alice has this infocoin. If so, they send the message "Yes, Alice owns the infocoin 1234567, now it can be transferred to Bob." As soon as a sufficient number of people spread this message on the network, everyone will update their blockchain, which will show that infocoin 1234567 is now owned by Bob, and the transaction is completed.
This protocol has many inaccurate elements at present. For example, what does it mean to say “enough people should broadcast this message”? What does “enough” mean? This cannot mean everyone on the network, since we do not know a priori who is on the Infocoin network. For the same reason, this cannot mean some fixed share of users on the network. We will not try to figure this out right now. Instead, in the next section I will point out serious problems in the approach that we described. By paying attention to this problem, we will have a pleasant side effect of creating the ideas above more understandable.
Proof of work
Suppose Alice wants to spend again in the protocol I just described. She can do this by taking control of the Infocoin network. Let's assume that it uses an automated system to configure a large number of individual identities (users), say, a billion, on the Infocoin network. As before, she is trying to pay the same infocoin to Bob and Charlie twice. But when Bob and Charlie ask the network to verify the transactions, Alice's additional users will fill up the network, announcing to Bob that they confirmed his transaction, and Charlie that they confirmed his transaction by deceiving one or both at the same time, accepting such a transaction.
There is a way to avoid this problem by using an idea known as proof-of-work. The idea is paradoxical and involves a combination of two other ideas: (1) (artificially) making confirmation of transactions costly for network users in the form of computer calculations; and (2) reward them for helping verify transactions. The reward is used so that people on the network try to help verify transactions, despite the need to spend computing power on this process. The benefit of verifying transactions is cost-effective, helping to avoid dependence on the number of identities (network users) controlled by someone. Thus, only the total computing power can put pressure on the test. As we will see, using some clever design, we can do so
Here is the essence of proof of proper operation. But in order to truly understand, we must look at the details.
Suppose Alice broadcasts the news “I, Alice, give Bob one infocoin with serial number 1234567” .
Upon hearing this message, everyone adds it to the queue of pending transactions: they are heard, but have not yet been approved by the network. For example, another network user named David may have the following queue of pending transactions:
I, Tom, give Sue one info-code, with serial number 1201174.
I, Sydney, give Cynthia one info-code, with serial number 1295618.
I, Alice, give Bob one infocoin with serial number 1234567.
David checks his copy of the blockchain and sees that every trade is good. He would like to help by sending news about the validity of transactions for the entire network.
Nevertheless, before doing this, as part of the verification protocol, David needs to solve a difficult computational problem - proof of correct operation. Without solving this problem, the rest of the network will not accept its verification of transactions.
What problem does David need to solve? To explain this, let h be a fixed hash function known to everyone on the network - it is built into the protocol. Bitcoin uses the famous SHA-256 hash functionbut any cryptographically secure hash function will do. Let's give David's queue of unfinished deals L label, so it’s more convenient for us to refer. Suppose David adds the number x (the so-called one-time number) and computes the hash sum from the combination. For example, if we use L = “Hello, world!” (Obviously this is not a list of operations, just a line is used to illustrate) and a one-time x = 0, then (we get the output in hexadecimal format)
h (“Hello, world! 0 ") = 1312af178c253f84028d480a6adc1e25e81caa44c749ec81976192e2ec934c64
The task that David must solve is proof of correct operationIs to find a prime number x so that when we add x to L and the result of the hash of the combination starts with a series of zeros. A task can be made more or less difficult by changing the number of zeros needed to solve this problem. A relatively simple proof of the correctness of the task can require only three or four zeros at the beginning of the hash, while a more difficult proof of the correctness of the task can require a much larger number of zeros, say 15 consecutive zeros. In any case, the above attempt to find a suitable one-time number with x = 0 failed, because the result does not start from scratch. Let's try x = 1 ,. Also does not work:
h ("Hello, world! 1") = e9afc424b79e4f6ab42d99c81156d3a17228d6e1eef4139be78e948a9332a7d8
We can continue to look for different values for x = 2,3,4 .... finally, with x = 4250 we get:
h ("Hello, world! 4250") = 0000c3af42fc31103f1fdc0151fa747ff87349a4714df7cc52ea464e12dcd4e9
This number gives us a string of four zeros at the beginning of the hash output . This will be enough to solve the simple task of "proof of work", but not enough to solve the more difficult problem of "proof of work".
There is a thing that makes this task difficult to solve. The result of the cryptographic hash function behaves like random numbers: change at least one bit in the source data and the result will radically differ so much that it is impossible to predict. So, if we want to have a hash value with 10 zeros at the beginning, then David will need to sort through, on average,
 different x values before he finds a suitable prime number. This is a rather complicated task requiring a lot of computing power.
different x values before he finds a suitable prime number. This is a rather complicated task requiring a lot of computing power. It is possible to make this task more or less difficult to solve through more or less number of zeros at the exit from the hash function. In fact, the Bitcoin protocol gains a fairly good level of control over the difficulty of the task, using a slight variation of the proof-of-work puzzle described above. Instead of requiring zeros, Bitcoin, as proof of proper operation, requires that the hash of the header of the transaction block be less than or equal to the number known as the target . This goal is automatically adjusted so that the Bitcoin block takes, on average, about ten minutes for authorization.
(In practice, there is significant chance in how much time it takes to approve a block - sometimes a new block is approved in just a minute or two, and in other cases it can take 20 minutes or even more. This changes directly in the Bitcoin protocol, so the time for verification, it usually reaches a maximum of about ten minutes. Instead of solving a single problem, we may require solving several problems; using a carefully designed software design, we can significantly reduce the variance in time for checking the block s Christmas tree.)
Ok, let's assume that David was lucky and he found the right number x. Hurrah! (He will receive a reward for finding the number, as will be described below). It translates the block of operations, which it claims, into the network along with the value of x. Other members of the Infocoin network can verify that x is a solution to proving the correctness of the task. And then they must update their block chains to include the new block of operations in the chain.
In order for the idea of proof of correct operation to have a chance of success, network users need an incentive to help them verify transactions. Without such an incentive, they have no reason to waste valuable computing power just to help verify other people's operations. And if network users are not ready to spend this power, then the whole system will not work. The solution to this problem is to reward people who help verify transactions. In particular, suppose we reward those who have successfully verified a block of transactions by crediting them with a certain amount of infocoins. The reward for infocoin is so great that it will give them an incentive to participate in the test.
In the Bitcoin protocol, this confirmation process is called mining. For each block of transactions verified, a successful miner receives a reward in bitcoins. Initially, this award was set at 50 bitcoins. But for every 210 thousand checked blocks (approximately once every four years), the reward is halved. This happened only once. To date, the reward for mining the block is 25 bitcoins. This half-rate cut will continue every four years until the year 2140. At that point, the mining reward will drop below 10 ^ -8 bitcoins per block. 10 ^ -8 bitcoins, in fact, is the smallest unit of Bitcoin, and is known as Satoshi . Thus, in 2140, the total supply of bitcoins will cease to increase. However, this will not eliminate the incentive to continue checking transactions. Bitcoin also makes it possible to allocate a certain amount in the transaction as a transaction fee, which will go to the miner, which helps to accept transactions. In the early days of Bitcoin, the transaction fee was zero, but with the popularity of Bitcoin, transaction fees gradually increased, and are now an additional addition to the reward of 25 Bitcoins for the mining block.
You can think of proof of work as a competition who accepts transactions faster. Each entry to the competition costs a bit of processing power. The chance that a miner wins the competition is (roughly speaking, and with some reservations) equal to the total processing power that they control. So, for example, if a miner controls one percent of all the processing power used to verify transactions in Bitcoin, then it has about one percent chance of winning. That is, provided that a lot of computing power is involved in the competition, a dishonest miner will most likely have a relatively small chance of distorting the verification process, unless he spends a huge amount of computing resources.
Of course, while this inspires inspiration, the dishonest side has only a relatively small chance to ruin the block chain, but this is not enough to inspire confidence in the currency. In particular, we have not yet fully resolved the issue of re-spending.
I will analyze double costs soon. Before doing this, I want to fill out an important detail in the Infocoin description. It would be ideal to coordinate the order in the Infocoin network in which the transactions took place. If we do not have such an order, then at any moment it may become unclear who owns which infocoins. To solve this, we will require that new blocks always include a pointer to the previous block approved in the chain, in addition to the list of transactions in the block. (The pointer is actually just a hash of the previous block). So, we have a block chain - it’s just a direct chain of transaction blocks, one after another, where each block contains a pointer to the immediately previous block:

Sometimes, a plug appears in a chain of blocks. This can happen, for example, if by chance two miners checked the block of operations at the same time - and both broadcast their newly approved block to the network, and some people will update their block chain in one direction, and others will update in the other direction:

It would seem that this causes a problem which we are trying to avoid - it is no longer clear in what order the transactions occurred, and this does not clarify who owns which infocoins. Fortunately, there is a simple idea that can be used to remove any plugs. The rule is this: if a plug suddenly happens, people on the network track both branches. But at any given time, miners only work on continuing the branching in which a copy of the block chain is longer.
Suppose we have a fork in which some miners get block A first and some miners get block B. Those miners who get block A first will continue to work along this branch, while other miners will go along with branch B. Suppose that miners working on branch B successfully mined a block:

After everyone receives the news that this has happened, miners working on branch A will notice that branch B is now longer and will switch to work on this branch. That's all! Immediately, the work on branch A will stop, and everyone will work on the same linear chain, and block A can be ignored. Of course, any unconfirmed transactions included in block A will still be waiting for decisions in the queues of miners working on branch B, and subsequently all transactions will be confirmed. In addition, it may turn out that miners working on branch A will expand it earlier. In this case, work on branch B stops quickly, and again we have one linear chain.
Regardless of the outcome, this process ensures that the block chain has a time-aligned ordering of transaction blocks. It is accepted in Bitcoin that a transaction is not considered confirmed before: (1) it is part of a block in a long branch, and (2) at least 5 blocks followed it in the longest branch. In this case, we say that the transaction has “6 confirmations”. This allows the network time to arrive at a consistent ordering of blocks. We will also use this strategy for infocoin.
We sorted out the streamlining, let's get back to thinking about what happens if a dishonest user tries to spend twice. Suppose Alice tries to spend an infocoin twice with Bob and Charlie. One of the possible approaches for her is to try to independently check the block, which includes both transactions. Assuming that she has one percent of the total computing power, she can get lucky, and she confirms the block by solving the mathematical problem of proof-of-work. Unfortunately, for Alice, the re-payment will be immediately noticed by other people on the Ifnokoin network and rejected, despite solving the problem with proof of correct operation. So we don’t need to worry.
A more serious problem arises if she broadcasts separately two transactions in which she conducts the same infocoin with Bob and Charlie, respectively. It can, for example, broadcast one transaction to one group of miners, and another transaction to another, hoping to obtain approval of transactions in this way. Fortunately, in this case, as we have seen, the network will finally confirm only one of these transactions, but not both. So, for example, Bob’s deal can ultimately be confirmed, in which case Bob can be calm. Meanwhile, Charlie will see that his deal has not been confirmed, and he will refuse Alice’s offer. So there is no problem. In fact, knowing that this will happen, there is no particular reason for Alice to try this.
There is another important option for double spending if Alice = Bob, i.e. Alice is trying to pay Charlie's coin, which she also “spends” to herself (that is, giving herself back). It looks like it’s easy to notice and deal with it, but at the same time, of course, it’s easy to set up several users connected to the same person or organization on the network, so this possibility must be taken into account. In this case, Alice’s strategy is to wait until Charlie accepts the infocoin, which will happen after the transaction has been confirmed 6 times in the longest chain. She will try to fork the chain before a deal with Charlie, adding a block that includes a payment transaction to herself:

Unfortunately, it is very difficult for Alice to catch up with the longer branch. Other miners do not want to help her, as they will work on a longer branch. And until Alice can solve the proof of correct operation, at least as fast as everyone else on the network together - roughly speaking, this means that controlling more than fifty percent of the processing power - she will simply lag further and further behind. Of course she might be lucky. We can, for example, imagine a scenario in which Alice controls one percent of the processing power, but luck happens and she finds six additional blocks in a row before the rest of the network finds any new block. In this case, she could get ahead, and gain control over the chain of blocks. But this particular event will happen with a probability of 1 / (100 ^ 6) = 10 ^ -12. A more general analysis in this direction shows that Alice’s probability of catching up with the longer branching of the blocks is infinitely small if she is not able to solve the proof of the correct operation at a speed close to all other miners combined.
Of course, this is not a thorough safety analysis, showing Alice's inability to make repeated expenses. This is just an unofficial argument of credibility. The original text representing Bitcoin, in fact, does not contain a thorough security analysis, only informal arguments on the points that I presented. The community that is interested in security is still analyzing Bitcoin and trying to understand possible vulnerabilities. You can see some of these studies here , and I will mention a few problems in “Problems for the author” below (see in the original test). At the moment, I think it's fair to say that the jury still does not know how secure Bitcoin is.
Ideas of proof of proper operation and mining raise many questions. What reward is needed to convince people to mine? How will changes in infocoin emissions affect Ifnocoin's economy? Will mining Infocoin ultimately be concentrated in the hands of a few, or many? If there are only a few miners, will this jeopardize system security? Presumably, the cost of transactions will balance over time - will this not lead to an undesirable source of friction, and will not make small transactions less desirable? These are all big questions that are beyond the scope of this article. I can return to these issues (in the context of Bitcoin) in future publications. Currently, we will focus on understanding how the Bitcoin protocol works.
Bitcoin
Let's move away from Infocoin and describe the actual Bitcoin protocol. There are a few new ideas here, but with one exception (see below) that they are basically obvious modifications of Infocoin.
In order to use Bitcoin in practice, we first install the wallet program on your computer. To give you an idea of what this means, here is a screenshot from a wallet program called Multbit. You can see the balance of bitcoins on the left - 0.06555555 bitcoin, or about $ 70 at the exchange rate for the day I took this screenshot - and on the right are two recent transactions that form 0.06555555 bitcoins:

Suppose you are a merchant who created an online store and decided to allow people to pay for your goods using Bitcoin. The first thing you do is generate a Bitcoin address in the program. In response, he will generate a public / private key pair, and then a public key hash to form his Bitcoin address:

Then you send the Bitcoin address to the person who wants to buy from you. You can do this by email, or even put the address publicly on a web page. This is safe, because the address is just a hash value of your public key, which can be safely known in the world anyway. (I will return later to the question of why the Bitcoin address is a hash, and not just a public key.)
The person who will pay you generates the transaction. Let's take a look at the data from a real transaction transmitting 0.31900000 bitcoins. The following shows almost raw data. They are changed in three ways: (1) the data was converted from serial to parallel (deserialized); (2) line numbers that have been added for ease of use; and (3) I shortened the various hashes and public keys by simply displaying the first six hexadecimal digits of each, when in fact they are much longer. Here are the data:
- {"Hash": "7c4025 ...",
- "Ver": 1,
- "Vin_sz": 1,
- "Vout_sz": 1,
- Lock_time: 0,
- "Size": 224,
- "In": [
- {"Prev_out":
- {"Hash": "2007ae ...",
- "N": 0},
- "ScriptSig": "304502 ... 042b2d ..."}],
- "Out": [
- {"Value": "0.31900000",
- "ScriptPubKey": "OP_DUP OP_HASH160 a7db6f OP_EQUALVERIFY OP_CHECKSIG"}]}
Let's go line by line.
Line 1 contains the hash of the remainder of the transaction, 7c4025 ..., expressed in hexadecimal. This is used as a transaction identifier.
Line 2 tells us that this is a deal in version 1 of the Bitcoin protocol.
Lines 3 and 4 tell us that the transaction has one input and one output, respectively. I will talk below about transactions with a large number of inputs and conclusions, and why this is useful.
Line 5 contains the value of lock_time, which can be used to control when the transaction is completed. For most transactions, Bitcoin today lock_time is set to 0, which means that the transaction is completed immediately.
Line 6 tells us the size (in bytes) of the transaction. Please note that this is not a cash transfer! About it further.
Lines 7 through 11 define the introductory bitcoins for the operation. In particular, lines 8 through 10 tell us that the input should be taken from the output from the previous transaction with the corresponding hash amount, which is expressed in hexadecimal format as 2007ae .... .n = 0 tells us that this will be the first conclusion from that transaction; we will see in the near future how several conclusions (and inputs) in a transaction work, so don’t worry too much about it now. Line 11 contains the signature of the person transferring the money - 304502 ..., then a space, and then the corresponding public key -04b2d .... Again in hexadecimal format.
The only thing that should be noted about the input is the lack of an exact indication of how many bitcoins from the previous transaction should be spent in this transaction. In fact, all bitcoins from n = 0 of the output of the previous transaction were spent. So, for example, if the n = 0th output from the previous transaction was 2 bitcoins, then 2 bitcoins will be spent in this transaction. This seems like an uncomfortable restriction - it’s the same as trying to buy bread with a $ 20 bill, and is not able to break it into small banknotes. The solution, of course, must have a mechanism for getting change. This can be done using transactions with several inputs and outputs, which we will discuss in the next section.
Lines 12 through 14 determine the withdrawal of bitcoins from the transaction. In particular, line 13 tells us the value of the output: 0.319 bitcoins. Line 14 is a rather complicated process. It is important to note that the value of a7db6f ... is the Bitcoin address of the intended recipient (written in hexadecimal format). Actually, line 14 is nothing more than a display of the Bitcoin scripting language. I am not going to describe this programming language in detail in this note, the main thing for us to understand is that a7db6f ... is only a Bitcoin address.
By the way, now you can see how Bitcoin is calling for a problem that I “tucked up my sleeve” in the last chapter: where do the Bitcoin serial numbers come from? In fact, the role of the serial number is played by the hash sum of transactions. In the transaction above, for example, the recipient receives 0.319 bitcoins that come from the first output of the previous operation with the hash sum 2007ae ... (line 9). If you go and look at the block chain for this transaction, you will see that its output comes from an even earlier transaction. Etc.
There are two smart things about using transaction hash amounts instead of serial numbers. Firstly, in Bitcoin there really are no separate, permanent (virtual) “coins”. There is simply a long series of transactions in a chain of blocks. It is a smart idea to understand that you do not need coins, and you can just get by with a book of deals. Secondly, when working in this way we remove the need for any central authority that issues serial numbers. Instead, serial numbers can be generated automatically, only by hashing the transaction.
In fact, you can continue to follow the chain of transactions further into the past. Ultimately, this process should be completed. This can happen in two ways. The first opportunity will arise when you come to the very first Bitcoin transaction contained in the so-called Genesis block . This is a special transaction that has no inputs, but only a conclusion in 50 bitcoins. In other words, this transaction sets the initial money supply. The initial block is accessed separately by clients (programs) of the Bitcoin network. And I will not go into details now, although this is very similar to the deal described above. You can see the serialized to parallel source data here .
The second possibility will be, when you follow the chain of transactions back in time, then in the end you will arrive at the so-called basic transaction (coinbase transaction). With the exception of the Start block, each block of operations in a block chain begins with a special underlying transaction. This deal is an award to the miner who will check this block of operations. It uses a similar but not identical transaction format presented above. I will not go into details on the format, and if you want to see an example, see here . You can read a little more about basic deals here.. In some ways, I was not accurate from the above, namely that it is specifically signed with a digital signature on line 11. Obviously, the payer must sign the entire transaction (except for the hash of the transaction that is generated later). Currently, this is not the case - some parts of the transaction are omitted. This makes some parts of the transaction changeable , i.e. they can be changed later. However, this plasticity is not included in the amount payable by senders and recipients, which cannot be changed later. I must admit, I did not fit into the details. As I understand it, this plasticity is under discussion in the Bitcoin developer community, and efforts are being made to reduce or eliminate this plasticity.
Operations with multiple inputs and outputs
In the last section, I described how a deal with one input and one output works. In practice, it is often very convenient to create a Bitcoin transaction with multiple inputs or multiple outputs. I will talk later about why this might be useful. But first, let's take a look at the actual transaction data :
- . {"Hash": "993830 ...",
- "Ver": 1,
- "Vin_sz": 3,
- "Vout_sz": 2,
- Lock_time: 0,
- "Size": 552,
- "In": [
- {"Prev_out": {
- "Hash": "3beabc ...",
- "N": 0},
- "ScriptSig": "304402 ... 04c7d2 ..."},
- {"Prev_out": {
- "Hash": "fdae9b ...",
- "N": 0},
- "ScriptSig": "304502 ... 026e15 ..."},
- {"Prev_out": {
- "Hash": "20c86b ...",
- "N": 1},
- "ScriptSig": "304402 ... 038a52 ..."}],
- "Out": [
- {"Value": "0.01068000",
- "ScriptPubKey": "OP_DUP OP_HASH160 e8c306 ... OP_EQUALVERIFY OP_CHECKSIG"},
- {"Value": "4.00000000",
- "ScriptPubKey": "OP_DUP OP_HASH160 d644e3 ... OP_EQUALVERIFY OP_CHECKSIG"}]}
Let's go line by line. This is very similar to a transaction with one input and one output, so I will do it pretty quickly.
Line 1 contains the hash of the rest of the transaction. This is used as a transaction identifier.
Line 2 tells us that this is a transaction of version 1 of the Bitcoin protocol.
Lines 3 and 4 tell us that the transaction has three inputs and two outputs, respectively.
Line 5 contains lock_time. As with one input and one output, the value is 0, which means that the transaction is completed immediately.
Line 6 tells us the size of the transaction in bytes.
Lines 7 through 19 define a list of entries for the transaction. Each corresponds to a conclusion from a previous Bitcoin transaction.
The first entry is defined in lines 8 through 11.
In particular, lines 8 through 10 tell us that the input should be taken from the n = 0th output from the transaction with a hash value of 3beabc .... Line 11 contains a signature, then a space, and then the public key of the sender of bitcoin.
Lines 12 through 15 define the second input in a format similar to lines 8 through 11. And lines 16 through 19 define the third input.
Lines 20 through 24 define a list containing two conclusions from the transaction.
The first output is defined on lines 21 and 22. Line 21 tells us the output value of 0.01068000 bitcoins. As before, line 22 is an expression of the Bitcoin scripting language. The main thing to pay attention to here is the line e8c30622 ... is Bitcoin address of the intended recipient of funds.
The second conclusion is defined in lines 23 and 24 in a form similar to the first conclusion.
One obvious oddity in this description is that although each output has an indication of the amount in bitcoin associated with it, this is not in the inputs. Of course, the values of the corresponding inputs can be found by referring to the corresponding conclusions in previous transactions. In the standard Bitcoin operation, the sum of all inputs in a transaction must be at least as much as the sum of all conclusions. (The only exceptions to this principle are the Initial block and basic transactions (coinbase), both form a new offer on the Bitcoin network.) If there are more inputs than outputs, then the excess is used as a transaction fee. This is paid to the miner for a successfully verified block in which the current transaction is included.
That's all about transactions with numerous inputs and outputs! They are a fairly simple transaction variation with one input and one output.
One good use of such transactions is the idea of surrender. Suppose, for example, that I want to send you 0.15 bitcoins. I can do this by sending you money from a previous transaction in which I received 0.2 bitcoins. Of course, I do not want to send you all 0.2 bitcoins. The solution will send you 0.15 bitcoins, and send 0.05 bitcoins to your Bitcoin address, which belongs to me. These 0.05 bitcoins are surrender. This is somewhat different from the process of receiving change in a store, because change in this case is a payment to oneself. But the general idea is similar.
Conclusion
This concludes the basic description of the basic ideas that lie in Bitcoin technology. Of course, I omitted many details - we did not do a technical description. But I described the basic ideas for the most common cases of using Bitcoin.
Although the rules of Bitcoin are simple and easy to understand, this does not mean that it is easy to understand all the consequences of these rules. There is much more to say about Bitcoin, and I will explore some of these issues in the future.
I will conclude my post by addressing a few controversial points.
How anonymous is Bitcoin? Many people claim that Bitcoin can be used anonymously. This statement has led to the formation of markets such as the Silk Road) and various successors who specialize in illegal goods. Meanwhile, the claim that Bitcoin is anonymous is a myth. The blockchain is public and open, which means an opportunity for everyone to see any Bitcoin transaction ever. Although Bitcoin addresses are not immediately associated with real people, computer scientists have done a great job figuring out how to de-anonymize"Anonymous" social networks. A block chain is an ideal target for these methods. I will be very surprised if the vast majority of Bitcoin users are not identified with a relatively high degree of confidence and ease in the near future. This confidence will not be high enough to achieve a guilty plea, but high enough to identify likely goals. In addition, identification will be retrospective, which means that those who bought drugs on the Silk Road market in 2011 will still be able to identify themselves based on the block chain, say, in 2020. These de-anonymization methods are well known to scientists, and, presumably, to the National Security Agency (USA). I would not be surprised if the NSA and other institutions have already recognized many users. Paradoxically that Bitcoin is often touted as anonymous. This is not true. On the contrary, Bitcoin is perhaps the most open and transparent financial instrument that the world has not yet seen.
Can you get rich with Bitcoin? Well, maybe. Tim O'Reilly once said: “Money is like gas in a car - you need to pay attention or you will end up on the side of the road; but a well-lived life is not a tour of the gas station! »A lot of interest in Bitcoin comes from people whose life position is aimed at finding a really big gas station. I have to admit, I find it puzzling. In my opinion, it is much more interesting and pleasant to think of Bitcoin and other cryptocurrencies as the path to new forms of collective behavior. It is intellectually fascinating, offers wonderful opportunities for creativity, is socially valuable, and you can also put money in a bank. But if money in the bank is your main task, then I believe that other strategies have a much greater chance of success.
I omitted the details: although this post described the main ideas behind Bitcoin, there are many details that I did not mention. Here, for example, is the size preservation feature that is used by the protocol, based on a data structuring model known as the Merkle Tree . This is a detail, but a great detail, and it’s worth knowing more if data structures are your thing. You can download and explore the original Bitcoin pages . Secondly, I have already talked a bit about the Bitcoin network - questions such as how the network deals with denial of service attack, how the nodes join and leave the network, etc. This is a fascinating topic, but it also requires a lot of detail, so I omitted that. You can learn more about this at some of the links above.
Scripting language Bitcoin: In this article I explained Bitcoin as a form of digital online money. But this is only a small part of a much larger and more interesting story. As we have already seen, each Bitcoin transaction is associated with a script in a programming language Bitcoin. The scenarios that we saw in this article describe simple operations like “Alice gave Bob 10 Bitcoins . ” But the scripting language can also be used to express much more complex transactions. In other words, Bitcoin is programmable money.. In later publications, I will explain the scripting system, and how you can use Bitcoin scripts as a platform for experimenting with all kinds of amazing financial instruments.
Translation: Andrey Dubetskiy, Igor Korsakov
