May 9, 2014 at 00:00May habrasovorevlenie: make your own GLONASS
It was a cold winter of 2063 ... you, sitting in a hut in the Siberian steppes, drinking hot tea, out of nostalgic motives took out your favorite rare smartphone of the 2014 model with GLONASS support - but for some reason he did not find a single satellite. Suddenly the piercing bell of the red government telephone cut the silence - the voice on the other side chattered: it turned out that all the GLONASS satellites were out of order due to an unknown malfunction ... (TZZh? Bookmarks? Who will understand now ...)Well, the hope is now only on you - you need to develop a new satellite navigation system as soon as possible (by Monday) taking into account the achievements of science and technology in 2063: due to the fact that fusion reactors and annihilation engines have become compact enough to fit on aboard the satellite - they are now fixed at one point in near-Earth space, there is no longer any orbit. Accordingly, almanacs and ephemeris (satellite orbit parameters) no longer need to be transmitted from satellite to earth.
The principle of operation of GLONASS in 2063
The thing is happening on a two-dimensional plane. It is known in advance that the receiver is guaranteed to be no further than 6378 km from the origin. Satellites are fixed at points distant from the center of coordinates at a distance of 10 thousand to 20 thousand km. Each satellite transmits the same pseudo-random sequence with a transmission speed of 1 Megabits (million bits per second), the signal we receive at a frequency of 10 million samples per second. Because each satellite transmits a signal at its own separate frequency - we can receive them independently.The pseudo-random sequence is repeated every second. The start of satellites transmitting a pseudo-random sequence and receiving a signal on the ground - ideally coincide, however, due to the fact that the distance from the satellites to the receiver is different - because of the speed of light we get a delayed signal (speed of light = 299792458 meters per second) - t. e. first we take the “tail” of the previous sequence, then the “head” of the current one. Having calculated the delay by shifting the code sequence, we can estimate the distance to the satellite. Knowing the distance to several satellites - we can roughly determine the coordinates.
Schematically, it will look like this: The radius of the drawn circle is the calculated signal delay multiplied by the speed of light.
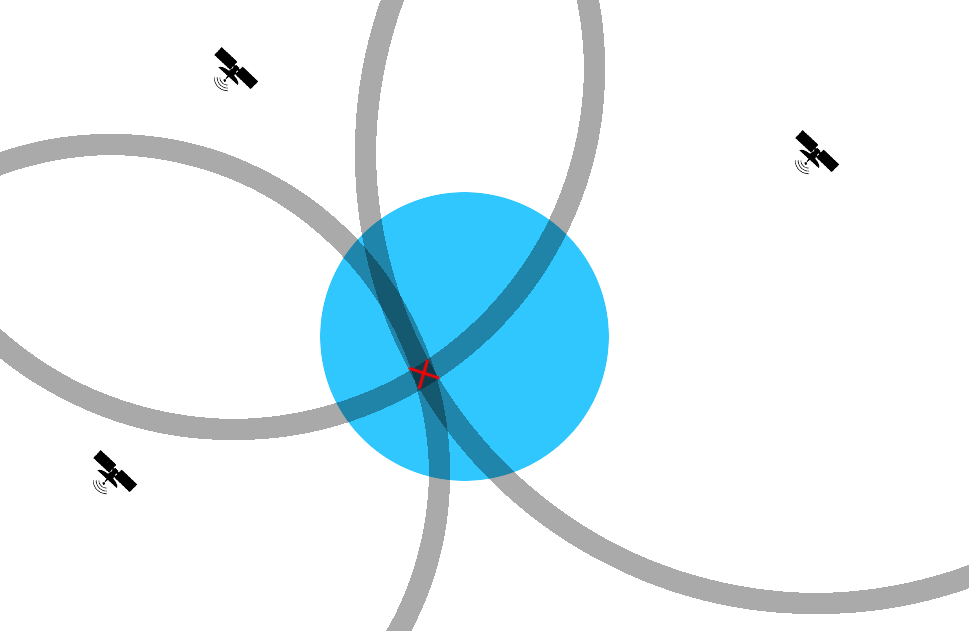
The satellites and the receiver stand still - there is no Doppler shift, and relativistic effects (including gravitational ones) need not be taken into account. Those. in time there are no tricks.
Input format
Data is entered through standard input.The first line is the number N from 2 to 255: the number of satellites.
Next, the description of N satellites: in separate lines - the X and Y coordinates of the satellite in meters, relative to the origin.
Next - 10 million digits 0 or 1, the pseudo-random sequence received from the satellite received on the ground.
Algorithm for generating a pseudo-random sequence (it is always the same):
data = md5("3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446"+to_string(pos))
Where pos - varies from 0 to 999999. If the first character is data> '7' - then one is transmitted, otherwise zero.
The receiver receives a signal with a sample 10 times more often, because 0 and 1 are repeated for 10 consecutive samples. More frequent sampling at the receiver allows you to more accurately determine the propagation delay of the signal.
Output example: (the received code sequence is partially shown)
2 -6.83616e + 006 1.6126e + 007 00000000000000001111111111000000000000000000000000000000000000 [...] -1.07643e + 007 -1.48409e + 007 10000000000111111111111000000000011111111111111111111111111111111111111 [...]
Output format
Results are printed to standard output.The real coordinates of the receiver, separated by a space - X and Y, in meters, relative to the origin.
If it is impossible to unambiguously calculate coordinates, it is permissible to derive any of the solutions.
Example output:
-1.81683e + 006 -1.74334e + 006
Examples of input / output files can be downloaded here: s.14.by/glonass-contest.zip
Evaluation of the results
If delta is the error in determining the coordinates in meters and T is the time taken to calculate, then the number of points is calculated by the formula 100 / (delta + 10) + 10 / (T + 1). If the operating time is more than 5 seconds on the i7-3820 processor with HT or the error in determining the coordinates exceedsProgramming language
Only Java SE 7 is allowed; third-party libraries cannot be used. The solution should be in one file, no larger than 20kB. You cannot work with the network, access any files on the local machine, work with native code (JNI and co).Making decisions, deadlines and where to send
Decisions are made until 23:59 (Moscow time) on May 11 at contest@14.by, the decision file must be attached to the letter - you do not need to insert the code in the letter itself!The first line of the solution should contain a comment of the form:
//@BarsMonster
Prizes
The first place in points - 2 BTC, thesecond - 1 BTC, the
third - 0.5 BTC.
Additional nomination:
For the most compact solution, passing all tests (in time and required accuracy) 1 BTC.
The results will be published on the hub on Monday-Tuesday, winners with read-only accounts will be invited to the hub, and of course we will try to invite the winners for an interview.
Afterword
Blowing off dust from a cabinet shelf, you took out an ancient folder signed “GLONASS: reference implementation”, probably containing the receiver implementation in one of the ancient programming languages ... Perhaps after a while you will be able to figure out what is written there ...Follow the updates of the article and all good luck!
Update 10/05/2014 2:03 : Corrected the description of the code sequence. Will be executed on 64-bit Java (-Xms10g -Xmx30g). Line feeds are not documented, it’s better not to lay it on.
Update 10/05/2014 10:23 : Data is guaranteed to be in the disk cache to test the solution, not the disk (I already know its speed, 500Mb / s).
Update 05/10/2014 13:18: Satellite rounding creates too many ambiguities. The accuracy of satellite coordinates is guaranteed up to 1mm (3 decimal places in meters). Download the new file - the 3rd test with high accuracy has been added to it. All tests for final testing are regenerated with high accuracy.
Update 05/11/2014 18:00 : Finally, the results of recognition of the text of the program came. It turned out that it was written in some ancient programming language with a strange name - Erener. It seems that the authors really liked the ancient money. Judging by the marginal notes - the speed and accuracy of work left much to be desired.
Hidden text
//Might have some OCR errors
$sx, "sy"=>$sy, "sq" => $sequence);
}
$ref = "";
//Calculate reference sequence
for($i=0;$i<10000000;$i++)
{
$hash = md5("3.1415926535897932384626433832795O28841971693993751O582O9749445923O78164O62862O8998628O34825342117O67982148O865132823O6647O938446".((int)((($i)%1OOOOOOO/1O))));
$ref .= ($hash[0]>'7')?"1":"0";
}
$ref .= $ref;
//Calculate pseudorange
for($i=0;$i<$n;$i++)
{
$sat[$i]["range"] = (10000000.0-intval(strpos($ref, $sat[$i]["sq"])))/10000000.0*299792458.0;//Meters
}
$best = 10E100;
for($x=-7000000;$x<7000000;$x+=2000)
{
for($y=-7000000;$y<7000000;$y+=2000)
{
$delta = 0;
for($i=0;$i<$n;$i++)
$delta += abs($sat[$i]["range"]-sqrt(pow($x-$sat[$i]["sx"],2)+pow($y-$sat[$i]["sy"],2)));
if($delta<$best)
{
$best = $delta;
$bestx = $x;
$besty = $y;
}
}
}
print("$bestx $besty\n);
echo "\n\nExecution time: ".(microtime(true)-$startTime);
?>
Update 05/11/2014 20:11 : Time is inexorably coming to an end - the flow of decisions is becoming increasingly stormy. Results will be published no later than Tuesday. The time of taking the latest decisions will be traced by a ruthless robot.
Update 05/14/2014 23:22 : Published results.