The task of changing the voice. Part 3. Applied Speech Representation Models: LPC

We continue the series of articles devoted to the task of changing the human voice, on the solution of which we are working at i-Free . In a previous article, I tried to briefly talk about the mathematical apparatus used to describe the complex physical processes that occur in a person’s speech path when making sounds. Issues related to the modeling of the acoustics of the speech tract were raised. Simplifications and approximations allowed in many cases have been described. The result of the article was to bring the physical model of sound propagation in the speech path to a simple discrete filter.

In this article, I want to continue the previous endeavors on the one hand, and on the other hand, to move a little away from the fundamental theory and talk about more practical (more “engineering”) things. One of the applied models, often used when working with a speech signal, will be briefly considered. The mathematical basis of this approach, as often happens, was originally laid in the framework of studies of a completely different direction. Nevertheless, the physical characteristics of the speech signal made it possible to apply these ideas precisely for its effective analysis and modification.

The previous article, due to the specifics of the issue under consideration, was oversaturated with scientific terms and formulas. In this - we will try instead of a detailed description of mathematical constructions to focus on the ideological concept and qualitative characteristics of the described model.

Next, we will examine in more detail the theory of the LPC model (Linear Prediction Coding) - a remarkable well-composed approach to the description of a speech signal, which in the past determined the direction of development of speech technologies for several decades and is still often used as one of the basic tools in the analysis and description of a speech signal .

Simplified discrete speech model

In this paragraph, we will make the transition from the discrete model of the speech tract from the last article (that model described only the propagation of sound in pipes with a constant cross-sectional area), to a more complete model that describes the entire articulation process. The main idea of ​​the model is formulated quite simply - imagine that the discrete signal y (n) * that we are analyzing is the output of a linear digital filter a ** h, through which some “exciting” signal x (n) passes:
_____________________________
* - hereinafter, we will talk only about discrete signals and we will replace the time variable t with a discrete reference index n
** - we immediately apologize for some references to English-language sources, but often the required question is more fully disclosed in one place, we hope the language barrier will not be a big barrier.



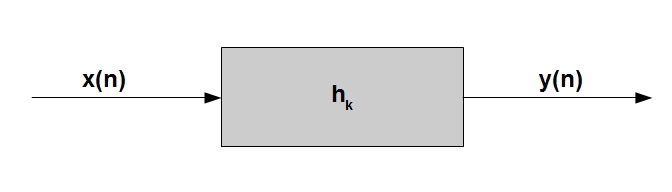
It is logical to assume that by changing the filter coefficients h_k, and, possibly, in some cases the “exciting” signal itself, it is possible to achieve a different sound of the output sound *. In words, everything is very simple, but now let's try to figure out what relation this completely abstract generalized idea can have to a speech signal.
_____________________________
* - as in the previous article, the symbol "_" we will denote the indexing operation, and the symbol "^" - the operation of raising to a power.

Briefly recall, but at the same time a little generalize what was said in the very first article. The formation of speech sounds can, with a few caveats, be described as follows:

1) the glottis in the larynx is the “basic” sound source (here, with the participation of the vocal cords, the same voiced or unvoiced excitation signal from article 1 is generated)

2) the organs of the vocal tract above the larynx are one complex acoustic filter that amplifies some and attenuates other frequencies

3) the “final touch" to the final sound adds the process of emitting sound waves by the mouth or nose

The last point can be neglected in some way, because this transformation over the signal can be approximated by differentiation and, accordingly, it is relatively simple to reverse its effect on the signal. The first two are a bit more complicated. Both process data are not stationary in time. When generating a voiced excitation signal, the period of closure and the degree of closure of the folds of the glottis in the larynx continuously changes, which causes a change in the duration and in the form of "laryngeal" air pulses: as a result, the intonation and intensity of the sound, the emotional color of speech, change. The speech tract above the larynx is one large movable acoustic filter, its chambers and bows, changing its geometry, they change the position of resonant (formant) and antiresonant frequencies - the type of pronounced voiced sound changes in terms of phonetics. When pronouncing unvoiced sound, the vocal folds do not work, and the larynx is the source of the noise signal. The work of the rest of the speech tract does not fundamentally change, and, as a result, the spectrum of noisy sounds of speech also has a formant structure, albeit somewhat less noticeable. The above can be illustrated by the following simplified diagram:



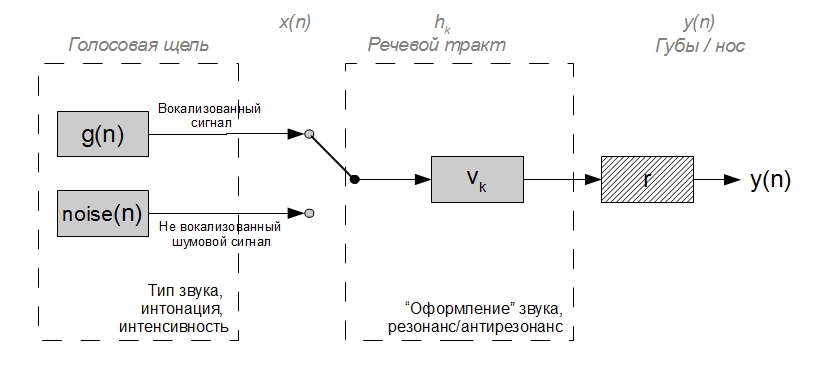
Corresponding elements from the 1st figure are indicated in gray font at the top.

In real life, there are a lot of nuances and mechanisms of the mutual influence of the vocal tract on the larynx and vice versa, as well as the respiratory apparatus on the entire acoustics of the vocal tract at the moment when the vocal gap is open. However, considering several “idealized” processes, we can say that this figure adapts the previous abstract idea of ​​an “exciting signal - filter - sound” to articulate speech sounds and at the same time takes rather well into account the basic properties of a real speech signal.

Advantages of this view on the process of sound production:

- the ability to consider the excitation signal of the vocal tract and its further propagation through the vocal tract independently of each other (in reality they are nevertheless interconnected, but this relationship is not always pronounced and in some cases it can be neglected)

- the ability to analyze the vocal tract as linear stationary (at short time intervals) systems

- the ability to well approximate most sounds in a speech signal

Of course, as it always happens in real life, this simplified approach is not so simple for practical use. A lot of uncertainties arise even at the stage of dividing the analyzed signal into voiced / unvoiced segments. Only for this task in the general case requires a complex signal processing with the involvement of a serious mat. apparatus. The next difficult moment is the non-stationary nature of the processes under consideration, and in this case, x (n) changes much more rapidly than h (n). To obtain reliable estimates of the parameters of this model, the most optimal is signal processing on time segments, the duration of which is a multiple of the period of the fundamental tone, which is not easy, given the fact that this period is constantly changing. It is also worth mentioning the limited applicability of this model for describing some consonants, in particular fricatives and "explosives." When pronouncing a loud fricative sound, a voiced exciting signal passes through a significant narrowing in one or another part of the speech path, which leads to the formation of strong turbulent noise. A deaf fricative is pronounced similarly, with the difference that the exciting signal is initially noise. Thus, the noise component of fricative sounds is largely formed already in the speech tract, and not just in the larynx, which is not taken into account by this model. “Explosive” sounds are a special case, the consideration of which we will omit for now. a voiced excitation signal passes through a significant narrowing in one or another part of the speech path, which leads to the formation of strong turbulent noise. A deaf fricative is pronounced similarly, with the difference that the exciting signal is initially noise. Thus, the noise component of fricative sounds is largely formed already in the speech tract, and not just in the larynx, which is not taken into account by this model. “Explosive” sounds are a special case, the consideration of which we will omit for now. a voiced excitation signal passes through a significant narrowing in one or another part of the speech path, which leads to the formation of strong turbulent noise. A deaf fricative is pronounced similarly, with the difference that the exciting signal is initially noise. Thus, the noise component of fricative sounds is largely formed already in the speech tract, and not just in the larynx, which is not taken into account by this model. “Explosive” sounds are a special case, the consideration of which we will omit for now. what is not taken into account by this model. “Explosive” sounds are a special case, the consideration of which we will omit for now. what is not taken into account by this model. “Explosive” sounds are a special case, the consideration of which we will omit for now.

We now turn from the generalized discrete model to specific application models that allow one to evaluate certain parameters of the speech signal.

Linear Prediction Coding Coefficients or simply LPC

The LPC method is uncomplicated with the generalized discrete speech signal model described above. Namely, the LPC coefficients directly describe the speech path V (see the previous figure). This description, of course, is not exhaustive and is some approximation of a real speaker system. However, according to theory, and as has been repeatedly proved by practice (to take at least the CELP algorithms used in modern cellular networks), this approximation is quite sufficient for many, many cases. The white spot in the LPC model remains the excitation signal of the speech tract, which in practice either does not change significantly, or, for example, is replaced by some previously calculated, as in CELP.

Let us describe more formally exactly what place the LPC coefficients in the system under consideration occupy. The signal at the input of the vocal tract (at the output of the glottis) will be further denoted as g [n]. For now, we will not focus on the nature of this signal - noise or harmonic. The signal at the output of the discrete filter, by which we approximate the speech path, will be denoted by v [n]. The LPC model thus solves the inverse problem - we will look for g [n], as well as the parameters of the filter, which turned g [n] into v [n], having at its disposal only v [n].

Recall the previous article, and the idea described in it of representing the vocal tract as a series of connected tubes. The main result of this approach is a convenient representation of the speech path in the form of a discrete filter (a system consisting of addition / multiplication / delay operations). Using algebraic transformations, it is possible to deduce from the difference equations describing a similar model its transfer characteristic of the form:



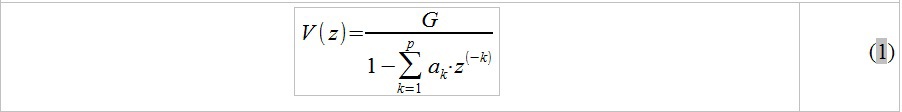
where G is some complex polynomial depending on the reflection coefficients r_k, a_k are some real coefficients that also depend on r_k, P is the number of pipes in the model under consideration. Since we consider the signal at short time intervals, it is fair to assume that the vocal tract is “immobile” during analysis, and, accordingly, the constant values ​​of the areas of articulated tubes with which we approximate the vocal tract (see the previous article). Based on this, we assume that the reflection coefficients r_k are constant, which, in particular, leads to a constant value of the polynomials G and a_k on the analyzed speech segment.

Algebra of reduction of difference equations describing the state of each tube in the composition of the speech tract (see previous article), we will not lead to this simple-looking equation, for obvious reasons. This equation itself is an important fundamental result - when considering the speech tract as a system of articulated tubes, it is possible to bring it to the form of a linear stationary system (LTS), namely an IIR filter containing only poles (looking ahead, we immediately say that these poles and correspond to formant frequencies so dearly loved by us). The operation scheme of such a system is shown below:



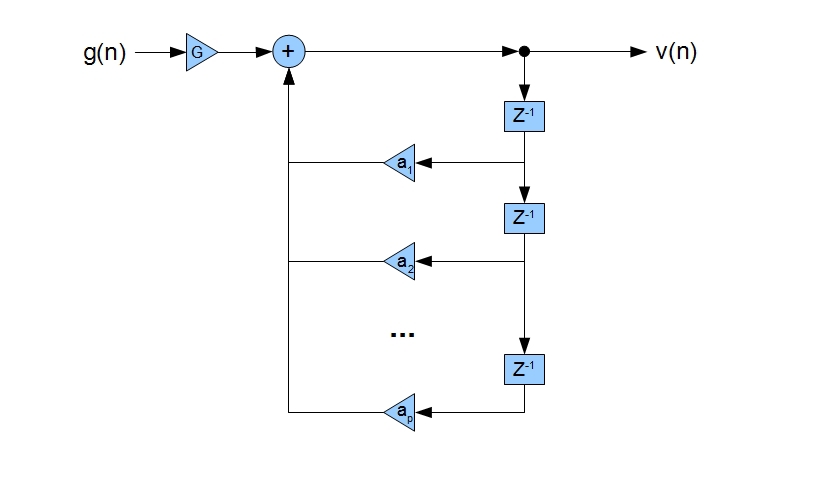
Using the transfer characteristic of the speech path specified above, it can be shown that the signal at the system output has the following form in the time domain:



A very interesting result: the complex process of sound production in the speech path reduces to the fact that the signal at the system output at time n is a superposition of the input signal at time n multiplied by a constant, and a linear combination of previous output samples at moments n - 1, n - 2 ... n - p. But let's not forget that this is of course just an approximation that ignores many details.

To obtain a description of the state of the speech tract in the analyzed speech segment, it is necessary to solve the problem of estimating the coefficients a_k and G. The adaptive filtering theory as a whole, and the LPC model in particular, allow us to solve this problem relatively simply and computationally efficiently. The resulting description of the vocal tract will be far from exhaustive, but sufficient for many tasks.

Finding LPC Coefficients

To solve the problem of estimating the coefficients a_k, it is convenient to introduce the concept of a linear prediction filter, the task of which is to obtain reliable estimates of the desired coefficients (the estimates will be denoted below as a'_k). The output of the prediction filter (v '(n)) can be subtracted from the signal at the output of the speech path (the resulting difference will be called the “signal-error" below):



e (n) - error signal. Coefficients a'_k together with G are called linear prediction coefficients, LPC-coefficients. In the case where the estimates a'_k are close to the true values ​​of a_k, e (n) will tend to G ∙ g (n). Note that the linear prediction filter in this problem is the inverse filter to our approximation of the speech path. If the estimates a'_k are close to the true a_k, then this filter (denoted by v ^ (- 1) _k) is able to reverse the influence of the speech path on the signal g (n) up to the constant G:



Let us return to the estimates a'_k. Having chosen a certain segment of the signal for analysis (suppose the length is M), using expression (3) we can obtain the error signal vector of a similar length. The question is how now, having a given vector, form consistent estimates a'_k? This problem can be solved usingleast squares method . To do this, a minimum of the function E_n is searched, the value of which is equal to the average of the sum of the squares of the signal-error values ​​over some analyzed time interval (the function E_n is nothing other than the standard error ). In other words, the parameters a'_k are sought for which the mean-square error function E_n takes a minimum value. The root-mean-square error itself in our case is expressed by the formula:



Finding the average implies dividing by the number of elements (multiplication by 1 / M), however, this factor will not affect the solution of the desired system, so it can be omitted.

Once again, for clarity, we describe what formula (4) expresses:

1) in the vicinity of the instant of time 'n', M samples of the signal are taken (as a rule, from n to n + M - 1). The number M depends on the sampling frequency of the signal and on our assumptions about the length of the stationarity interval of this signal.

2) For the selected samples, an expression is compiled corresponding to the prediction error e (m), m = n: n + M-1

3) The average of the squares e (m) is found (in the expression for the average, we omit the division by the number of members of the sum).

4) We will minimize the obtained average E_n (which is a function of the reference number n).

Why is the mean square error used as a measure of the reliability of our prediction filter? Firstly, it is a good numerical approximation of the variance of a random process in some cases. If we assume that our error is distributed normally and our prediction filter is not strongly biased, then the mean-square error will tend to the variance D [e (m)] and we, therefore, look for the minimum variance of our error signal. Secondly (although this is rather not a reason, but a convenient consequence), this function is very convenient to differentiate by the desired a'_k, namely, it is convenient to search for the minimum of the function with the help of differentiation.

Having opened the square sign under the sum in (4) and equating to zero the values ​​of the derivatives E_n for each a'_k, it is possible to obtain a system of P linear equations of the form:



We will not give a detailed derivation of (5) from (4) either - for this we need to apply several formulas from school algebra and some formulas to convert certain sums . The system of equations (5) is the “main core” in the LPC algorithm. Index i corresponds to the equation number in the system (the number a'_k, according to which the derivative was taken) and, like index k, all values ​​from 1 to P go through. Recall that P corresponds to the number of tubes in the model approximating the speech path. The same number is called the linear prediction order. The solution of systems of linear algebraic equations is a separate applied field with its own mathematical apparatus, therefore we will not delve into this problem. We will only say that to solve a specific system (5), taking into account its properties, they are usually usedCholesky decomposition or Levinson-Darbin recursion

Having solved a system of P equations from P unknowns, we obtain estimates a'_k, and it remains only to find the gain G. In the LPC method, the estimate G is found after estimating a'_k, assuming that the signal is the input of the filter V is either a discrete delta function shifted at time n (a single pulse at time n) or white noise. In both cases, G can be found from the relation:



The conclusion of this formula is exclusively mathematical (that in the case of the delta function, that in the case of white noise) and how to explain the popular physical meaning of this formula, the author of the article does not present - let us leave it as it is. However, the very assumption that the input signal suddenly became a single pulse or white noise should be explained in more detail.

Strictly speaking, at the exit of the glottis in the larynx - at the entrance of the vocal tract, we have either a "larynx" impulse or a colored noise signal, but not a delta function or white noise. And here in the LPC theory is a very tricky "feint with ears." We imagine the larynx as part of the vocal tract and say that it was precisely in the larynx that either a single impulse or white noise entered. The concept of the speech path is thus somewhat expanded within the framework of our model, and in order to take into account the new model the effects that make a “laryngeal” pulse from a single pulse and colored noise from white noise, we increase the order of linear prediction P. Moreover, we go further, and include in our “LPC filter” effects associated with signal emission, which is also compensated by the addition of additional coefficients. These operations correspond to an increase in the length of our pole filter, by which we approximate the speech tract, which will lead to an increase in the number of its poles, and it is these additional poles that are responsible for the imaginary transformation indicated above. Obviously, in this case, the LPC model no longer fully corresponds to the initial discrete filter approximating the speech path. However, ideologically, these two approaches remain very close, if not “related”. It is not possible to reconstruct the excitation signal of the vocal tract g [n] with the help of LPC, as we initially wanted it. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks. by which we approximate the vocal tract, which will lead to an increase in the number of its poles, and it is these additional poles that are responsible for the imaginary transformation indicated above. Obviously, in this case, the LPC model no longer fully corresponds to the initial discrete filter approximating the speech path. However, ideologically, these two approaches remain very close, if not “related”. It is not possible to reconstruct the excitation signal of the vocal tract g [n] with the help of LPC, as we initially wanted it. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks. by which we approximate the vocal tract, which will lead to an increase in the number of its poles, and it is these additional poles that are responsible for the imaginary transformation indicated above. Obviously, in this case, the LPC model no longer fully corresponds to the initial discrete filter approximating the speech path. However, ideologically, these two approaches remain very close, if not “related”. It is not possible to reconstruct the excitation signal of the vocal tract g [n] with the help of LPC, as we initially wanted it. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks. that in this case, the LPC model no longer fully corresponds to the initial discrete filter approximating the speech path. However, ideologically, these two approaches remain very close, if not “related”. It is not possible to reconstruct the excitation signal of the vocal tract g [n] with the help of LPC, as we initially wanted it. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks. that in this case, the LPC model no longer fully corresponds to the initial discrete filter approximating the speech path. However, ideologically, these two approaches remain very close, if not “related”. It is not possible to reconstruct the excitation signal of the vocal tract g [n] with the help of LPC, as we initially wanted it. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks. does not seem possible. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks. does not seem possible. Nevertheless, the final approximation of the frequency response of the vocal tract (coefficients a'_k) obtained using the LPC is quite accurate for many tasks.

Once talking about choosing the order of P, it is logical to give some general recommendations on his choice. It is believed that, on average, formant frequencies in a speech signal are located at a density of about 1 formant per kilohertz. Then, since each complex pole of our model filter corresponds to one formant frequency, it is convenient to choose the order as:



where [] is rounding to the nearest integer, Fs is the sampling frequency of the signal in hertz. To compensate for the effect of combining the larynx and the vocal tract, as well as to take into account the effect of signal emission by the lips / nose in the model, various sources recommend increasing P by an additional 2-4 factors. That is, for work, for example, with a 10 KHz signal, the order P can be chosen equal to 12-14 coefficients. Some authors also advise applying the density of “1 formant at 1200-1300 Hz” when analyzing a female voice. This is due to the shorter length of the vocal tract in women and, as a result, to higher values ​​of formant frequencies in female voices.

LPC Summary

What ultimately gives us the calculation of LPC coefficients for a certain signal:

1) The output of the LPC calculation algorithm is a set of numerical coefficients that describe the pole filter. These coefficients in pure form allow us to obtain an expression for the output of a given filter in the time domain (expression (2)), as well as a general view of its z-characteristic (expression (1)). Since this filter is a pole filter, it is based on recursion and it is not possible to express the impulse response for such a filter. Using the z-characteristic, however, a complete analysis of the resulting filter is possible in both the time and frequency domains.

2) Если разложить на множители знаменатель полученной z-характеристики, становится возможным найти численные значения частот, соответствующих полюсам данного фильтра. Эти же значения хорошо аппроксимируют формантные частоты речевого тракта на анализируемом сегменте речи. (Правда стоит добавить, что точность аппроксимации зависит от грамотного выбора базовых параметров LPC — порядка P, длительности анализируемого интервала M, времени начала анализа n. Для общего случая автоматизировать этот выбор не так просто.)

3) Полученный с помощью LPC сигнал-ошибка (сигнал возбуждения дискретного фильтра, которым мы аппроксимируем процесс звукообразования) выходит похожим либо на белый шум, либо на смещенную во времени дельта-функцию. (данный пункт наиболее активно эксплуатируется при сжатии речи)

The logarithmic spectrum of a signal obtained by a conventional FFT and using LPC is shown below for example. The vowel A, pronounced by a male voice, was processed.



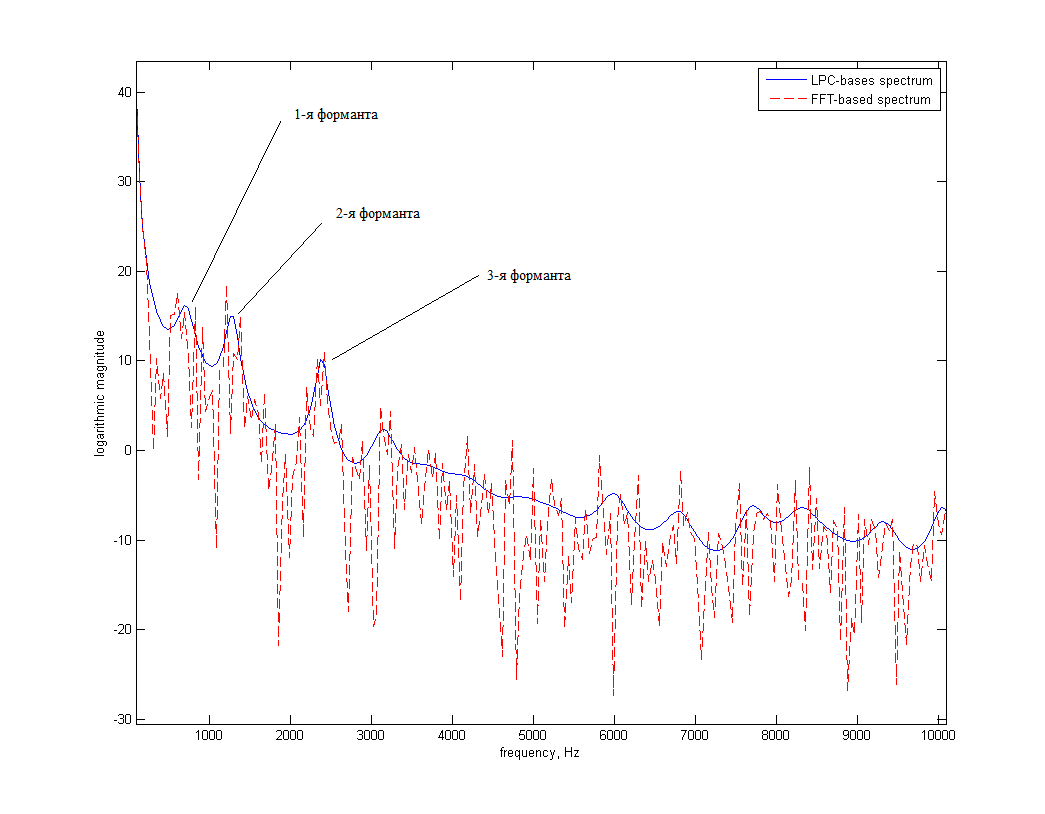
As you can see, the "LPC spectrum" is some smoothed version of the usual "FFT spectrum." In this case, the formant frequencies are manifested by “bright” local maxima, which is a good “start” for their detection and tracking.

The use of LPC for the analysis of the voice path

As mentioned in the previous article, when representing the speech tract in the form of articulated pipes of a fixed diameter, it is possible to approximate the processes that occur inside each pipe when sound propagates along the tract using difference equations. In this case, the equations will depend on the reflection coefficients r_k, where k is the number of the pipe under consideration. These coefficients, in turn, depend on the ratio of the area of ​​the pipe in question to the area of ​​the pipe following it. The boundary conditions (the first tube after the larynx and the last before the lips) are taken from special formulas that depend on the corresponding acoustic impedances, which in turn can in most cases be tabular functions. Earlier in the article, without proof, the fact was cited that, from the set of discrete difference equations describing such a system,

LPC analysis itself is a fairly “straightforward” and efficient method. The question may immediately arise, but is it possible, by calculating the LPC coefficients of a certain signal, to somehow restore the parameters of the speech path? You cannot give a 100% positive answer to this question. On the one hand, LPC coefficients are polynomials in r_k, and it is practically possible to do the opposite operation - restore r_k from a'_k. To do this, you can apply the transition stage in the form of PARCOR (partial correlation) coefficients. That is, from the LPC coefficients, calculate the PARCOR coefficients, and from them r_k. However, there is one complicating circumstance: the effects associated with the passage of the signal through the larynx and its radiation in the region of the lips are included in the LPC model, which does not correspond to the model of the speech path in the form of a discrete filter from the previous article (the number of pipes in the model of the speech path is no longer equal to the linear prediction order P). If you somehow reverse the effect on the larynx and radiation signal and conduct an LPC analysis of this modified signal, it is possible to obtain more consistent estimates of the reflection coefficients based on LPC. Again, it is worth remembering that even in this case, the reflection coefficients can only show the ratio of the areas of adjacent pipes in the speech path model - without any initial approximations, it will not be possible to restore the absolute values ​​of the areas. That is, we will be able to restore some function that repeats the area of ​​the vocal tract, but differs from it by some scaling factor.

There are many works whose authors solve the problem of reconstructing the function of the area of ​​the vocal tract, and in these works the LPC coefficients occupy not the last place in the used mathematical tools. In particular, LPC is often used as a basic method for determining the formant frequencies with which the function of the area of ​​the speech tract is already restored.

The approach to the analysis of the area of ​​the speech tract using LPC itself has many errors associated with the assumptions that we initially make, assuming a linear discrete filter as a model of the speech tract - a lot of this was said in the previous article. Research on this topic has been and is ongoing, good results have been achieved, but it is really impossible to restore the function of the area of ​​the vocal tract today in the general case, either using LPC or using any fundamentally different approaches.

conclusions

This article briefly describes the main ideas and ideology of the LPC model for representing a speech signal. This model is one of the most commonly used in the field of speech processing and, despite its fundamental limitations, gives very good estimates of real physical phenomena. Most often, this model is used for tasks:

- speech compression

- analysis of formant frequencies

- analysis of the speech path (as an auxiliary tool)

In the next article we will talk about the HPN-model (Harmonics-plus-noise) of a speech signal, in which the speech signal in explicitly divided into voiced and unvoiced components.

References:
[1] JL Flanagan. Speech Analysis, Synthesis and Perception.
[2] LR Rabiner, RW Schafer, Digital Processing of Speech Signals // (the main source of this article)
[3] I. Solonina Fundamentals of Digital Signal Processing, 2nd Edition // (a good short, but a bit “dry” explanation as an instruction for use)
[4] Mark Hasegawa-Johnson, Lecture Notes in Speech Production, Speech Coding, and Speech Recognition
[5] G. Fant. Speech Acoustics and Phonetics. Selected Writings .