How to lie with statistics

There are three types of lies: lies, blatant lies and statistics ( source )

There is such a wonderful genre - " bad advice " in which children are given advice, and children, as you know, do everything the other way around and everything turns out just right. Could it be the same with everything else?

Statistics, infographics, big data, data analysis and data science - who is not busy right now. Everyone knows how to deal with all this correctly, it remains only for someone to write how NOT to do this. In this article, we will do just that.


Hazen Robert " Curve fitting ". 1978, Science.

Article structure:

1. Introduction
2. Biased sampling (sampling bias)
3. Correctly choose the average (Well-chosen average)
4. And 10 more unsuccessful experiments that we did not write about
5. Playing with the scale
6. Choose 100%
7. Hide the desired numbers
8. Visual metaphor
9. Quality visualization example
10. Conclusion and Further Reading

Biased sampling (sampling bias)

In 1948, during the presidential race in the United States on the night of the announcement of the election results of Truman (Democrats) against Dewey (Republicans), the Chicago Tribune published its perhaps most famous DEWEY DEFEATS TRUMAN headline (see photo). Immediately after the closure of the sections, the newspaper conducted a poll, phoning a huge (sufficient for the sample) number of voters, and everything foreshadowed Dewey's resounding victory. In the photo we see laughing Truman, the winner of the 48th election. What went wrong?



People were called up really randomly and in sufficient numbers, but in the 48th year the phone was available only to people of a certain income and was rarely found in people with low incomes. Thus, the polling method itself amends the distribution of votes. The sample did not take into account a sufficiently wide stratum of Truman voters (as a rule, Democrats have a large share of the vote among the poor), for whom the phone, in turn, was unavailable. Such a sample is called biased sampling bias .

Folk art about this phenomenon:

According to online voting, 100% of people use the Internet.

Alumni salary

No one was surprised that when we hear about the salaries of university graduates, then for some reason it is always implausibly high numbers? In the US, it even comes to courts , where graduates claim that salary data is artificially high.


(picture from How to Lie with Statistics )

This is a fairly old problem, according to Darrell Huff, a similar question arose for 24 year old Yale graduates. And in fact, everyone is telling the truth, but not all. Statistics were collected in the form of polls (and in those years by paper mail). Not all send an answer, but only a small part of all graduates; those who are doing well are most actively responding (which often results in a good salary), so we only see the “good” part of the picture. This creates the bias of the sample and makes the results of such surveys completely useless.

Correctly choose the average (Well-chosen average)

Imagine a company in which a manager receives 25 thousand, his deputy 7.6 thousand, top managers 5.5 thousand, middle managers 3.5 thousand each, junior managers 2.5 thousand, and ordinary workers 1. 4 thousand (abstract pounds) per month.

And our task is to present information about the company in a positive light. We can write the average salary in a company is X, but what does mean mean ? Consider the possible options (see the diagram below):


(picture from How to Lie with Statistics ) The

arithmetic mean of some finite set X = {x _i } is a number m equal to mean (X) from the equation:



This is the most useless information from the point of view of the employee - 3,472 average salary, but how do you get such a high figure? Due to the high salaries of management, which creates the illusion that the employee will receive the same. From the point of view of the employee, this value is not particularly informative.

Of course, folk art did not bypass this feature of "average size" in the form of arithmetic mean

Officials eat meat, I - cabbage. On average, we eat cabbage rolls.

The median of a certain distribution P (X) (X = {x _i }) is such a quantity m that it satisfies the following equation:



Simply put, half of the workers receive more than this value, and half less - exactly the middle of the distribution! These statistics are quite informative for the company’s employees, as it allows you to determine how the employee’s salary is related to most employees.

The mode of the finite set X = {x _i } is the number m that occurs most often in X. In this case, fashion may be the most informative for a person who is going to start working in this company.

Thus, depending on the situation under the averagecan be understood any of the above values ​​(in principle, and not only of them). Therefore, it is fundamentally important to understand how this average value is calculated.

And 10 more unsuccessful experiments that we did not write about

Let’s put the regular newspaper in sulfuric acid, and the TV Park magazine in distilled water! Did you feel the difference? Nothing happened to the magazine - the paper is like new! (The whole video is here .)



Our research reports that Doake's toothpaste is 23% more effective than its competitors, all thanks to Dr Cornish's Tooth Powder! (Which probably contained β-carotene and the secret formula of the forest - author's note.) You will probably be surprised, but the study really did and even released a technical report. And the experiment really showed that toothpaste is 23% more effective than competitors (whatever that means). But is this the whole story?

In fact, the sample for the experiment was only a dozen people (according to Darrell Huff and the book already mentioned). This is exactly the sample that is needed to get any results! Imagine that we flip a coin five times. What is the probability that the eagle will fall all five times? (1/2) ⁵ = 1/32. Just one thirty-two, it can't be just a coincidence if all five eagles fall out, right? Now imagine that we are repeating this experiment 50 times. At least one of these attempts will succeed. We will write about it in the report, and all other experiments will not go anywhere. This way we get extremely random data that fits perfectly into our task.

Playing with the scale

Suppose tomorrow you need to show at a meeting that we have caught up with competitors, but the numbers do not converge a bit, so what to do? Let's move the scale a bit! Even the New York Times, known for its high-quality work with data, has released such a completely confusing chart (pay attention to the jump from 800k to 1.5m in the center of the scale).



(Example from How to Display Data Badly Howard Wainer. The American Statistician, 1984.)

Choose 100%

Imagine that last year milk cost 10 kopecks per liter and bread was 10 kopecks per loaf. This year, milk fell in price by 5 cents, and bread rose by 20. Attention is the question, what do we want to prove?

Imagine that last year is 100%, the basis for the calculations. Then milk fell in price by 50%, and bread grew by 200%, an average of 125%, which means that in general prices rose by 25%.


Let’s try one more time, let the current year be 100%, so milk prices were 200% last year, and bread 50%. So, last year, prices were on average 25% higher!


(graphs and example from the chapter "How to Statisticulate" How to Lie with Statistics )

Hide the desired numbers

The best way to hide something is to divert attention. For example, consider the dependence of the number of private and public schools (in thousands of units) by year. The graph shows that the number of public schools is reduced, and the number of private schools does not change significantly.



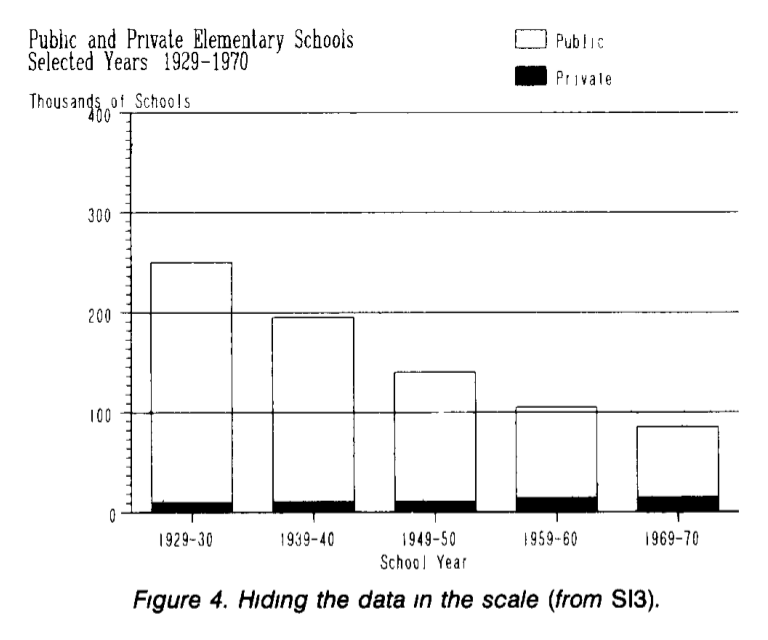
In fact, the growth in the number of private schools is hidden against the background of the number of public schools. Since they differ by an order of magnitude, virtually any changes will not be noticeable on the scale with a sufficiently large step. We will redraw the number of private schools separately; Now we clearly see a significant increase in the number of private schools, which was “hidden” in the previous chart.


(example and graphs from How to Display Data Badly, Howard Wainer . The American Statistician, 1984.)

Visual metaphor

If there is nothing to compare with, but you really want to confuse, then it's time for incomprehensible visual metaphors. For example, if instead of the length we depict the area on the graph, then any growth will seem much more significant.

Consider the consumption of beer in the USA for 1970-1978 in millions of barrels and the market share of Schlitz (see chart below). It looks good, impressive. Is not it?



And now let's get rid of unnecessary “garbage” on this graph and re-draw it in its normal form. Already somehow not so impressive and serious comes out.


(graphs and examples from John P. Boyd, lecture notes How to Graph Badly or What. NOT to Do )

The first picture does not lie, all the numbers in it are correct, only it implicitly presents the data in a completely different light.


(picture from How to Lie with Statistics).

Quality visualization example

High-quality visualization first of all presents the results, avoiding ambiguity, and conveys a sufficient amount of information in a compressed volume. About the work of Charles-Joseph Minard it is well said here :

Everything is perfect here, the viewer is not held for an idiot, and they do not spend his time sticking in censored . A wide beige strip shows the size of the army at each point of the campaign. In the upper right corner is Moscow, where the French army comes and where the retreat begins, shown by a black stripe. A timeline and temperature are tied to the retreat route for added interest.

The conclusion is: the amazed viewer compares the size of the army at the start with the fact that he returned home. The audience is full of feelings, he learned new things, he felt the scale, he is fascinated, he realized that he did not know anything at school.

(Charles Joseph Minard: Napoleon's Retreat From Moscow (The Russian Campaign 1812-1813), 1869.)

Conclusion and Further Reading

76% of all statistics taken from the head

This selection covers a far from complete list of techniques that consciously and also not consciously distort data. This article first of all demonstrates that we must very carefully monitor the statistics provided to us and the conclusions made on their basis.

Short list for further reading:
How to Lie with Statistics - a wonderful little book, incredibly interesting and well written, read in one go. Demonstrates the main "mistakes" that the media (and not only them) make when working with data.
How to Display Data Badly. Howard wainer The American Statistician (1984) - a collection of typical errors and general “harmful” rules, most often found in works with data visualization.