Analysis of VK friendships with Wolfram Mathematica

Not so long ago, a Wolfram Research seminar was held in Moscow. The era of Wolfram technologies , which told a lot of interesting things about one of the most powerful and definitely the most convenient computer research system Wolfram Mathematica . In particular, the results of a study of the data of the social network facebook by the research group “Constructive Cybernetics” were presented. A little earlier, I came across new Wolfram | Alpha features for comprehensive analysis of facebook page . And after all this, I had a crazy idea in my head: “I want to see the graph of friendly connections of the social network in which I live (namely, on the account)” . And I still found the time to implement it. Welcome to cat.


Interaction with the VK API begins with the creation of a Standalone application at https://vk.com/dev (there you can also edit an already created application). After a few clicks and a lot of thought over the name, the system issues the application ID , which will be used to obtain Access Token .
To get Access Token , you need to follow the link below, replacing the trellis with the application ID . You can read about how a line is formed here .

https://oauth.vk.com/authorize?client_id=######&scope=friends&redirect_uri=https://oauth.vk.com/blank.html&display=page&v=5.16&response_type=token

After that, a lot of useful information will appear in the address bar, in particular, access_token and user_id. These two values ​​must be saved. I named the variables myID (Integer || String) and token (String).
The next step is to write a basic function that interacts with the API. The standard response format from the VK API is JSON , which is easily parsed into lists and rules using Mathematica's internal tools .



The list of methods that are now available is limited only by the value of the scope parameter , which was passed during the formation of Access Token . To check the performance of the system, you can find out what your name is.



The VK API output contains a lot of unnecessary, therefore, to highlight only useful data, you must first cut off the unnecessary



And, then, apply the replacement rules (and this is a list of replacement rules) to those parameters that are interesting. Other rules are automatically ignored.



Thus, you can write a module that receives the username and (if desired) its photo.



Note that the parameter for the API is called user_ids , not user_id . This will allow you to get information about the whole list of users in one request (IDs must be separated by commas and there must be less than 1000).

Now you need to find users who are interested in learning something. Get a list of friends. In general, the whole function looks as follows.



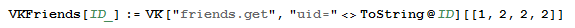
But due to my desire for idealism and the desire to come at least a little closer in thought to built-in functionsMathematica , my VKFriends has grown into this.



However, the " Clean" version will be used to build the graph . The following is interesting here: if you remove the fields parameter , the response from the API will be a list of IDs and nothing more. And if fields at least something, yes equal, the username is automatically included in the response. Therefore, for the version without avatars, the value fields = sex is appliedjust because sex is a beautiful word. In practice, the replacement rule for the floor in the final version is not implemented. Although you can always add fields that you are interested in exploring with your friends and build beautiful histograms from them, but then the code will grow many times more and its structure will need to be changed (unless, of course, strive for mass character).

The last function that the API needs to collect data is mutual friends. With their help, it will be possible to investigate connections only within your circle of friends, without receiving or processing megabytes of unnecessary information about who your friends from those you do not know. To bring syntax and features in line with VKFriends , I had to sweat a bit. The fact is that friends.getMutualit can only return a clean list of IDs, but this is not clear (if suddenly someone needs clarity)



That's it! On this, integration with the VK API for this task is over (and so much more than necessary). It's time to take the bull by the horns lists by the tails. Go!



We get a list of friends, describe the connection. All of them are associated only with you. Speed ​​of execution - a blink of an eye.



But do not worry, you will have time to go for tea and even drink it. Friends.getMutual itself is not particularly fast, so it must be executed for each of your friends. On my 333 friends, it took 119 seconds. This is the longest operation in the entire study. While this function works, you can put a kettle and choose tea. DeleteCasesarose in the process of debugging when the depth of the resulting array turned out to be suddenly 7. And all because friends have users for whom common friends are unavailable for some reason. And the error message is presented in the form of rules. Therefore, having deleted all the rules, the depth of the array will become normal, and the data type will become Integer (represented as String).
As a result of the code execution, the friendsOfFriends variable will have a two-dimensional list, the size of Length [myFriends]. And each element of myFriends (friend) will have a list of your mutual friends with this friend. Now you need to connect each friend from myFriends with all the friends from friendsOfFriends corresponding to him. Fuh. It seemed to explain with words, but if you use the attached Map for this, it will be completely unreadable. Therefore, we mischief a little in the procedural style (please do not repeat it yourself. This is a very bad style for Mathematica. Assembler was based on goto and in procedural programming it became a bad style, but Wolfram Language allows you to solve everything analytically, and explicit cycles are bad style [ purely formally this makes it the language of a new generation])



Next, you can try to build this graph, but nothing will come of it. Undirected graphs with vertices of degree greater than one are added only in the not yet published Mathematica10. The degree of all vertices of a non-digraph is equal to two, because each user who is friends with another user is also friends with the first. Simply put, we found a mutual friend B with user A, and when we looked at page B, user A also ended up in mutual friends. And after exploring the entire network, all users began to connect with two edges. To see this, replace UndirectedEdge with DirectedEdge for all occurrences. But the digraph is exactly 2 times redundant, so you need to get rid of repeated edges and build an undirected graph.



I had to write my own verification function, because there is none. And, for one, we connect the graphs together. Oddly enough, it works for quite a while ... As a result, the number of links should be reduced a little less than half, because the links from gMyFriends are not duplicated.
Well, everything can be built! Only nothing will be incomprehensible. So we continue to code until it becomes clear.

To make it clear, you need to change the appearance of the vertices of the graph. This can be done option VertexShape function Graph . VertexShape accepts a list of rules for replacing names with any objects. The vertex names in this case are a list of gMyFriends , expanded by only one element - by the user myID. Thus, it is necessary to obtain information for all elements of the Append list [myFriends, myID] and make this rule. Remember the boiled kettle? It's about time. You have a couple of minutes to drink tea.



What is cool is that all the info is requested immediately in one request. You just need ToString@Append[myFriends, myID] to remove the brackets and spaces from the brackets.
Now we have an array of what needs to be replaced and an array of what needs to be replaced. But no, not at all. Everything needs to be beautiful.



First, rectangular frames with a name and an avatar are constructed, then they are placed in a three-level list next to the corresponding IDs, and then in each element of the list from lists, the function header is changed from List to Rule. As a result, we get the list of rules from the list of lists. (Well, reallyWolfram Language is not perfect?)

Now everything is for sure!



You can enjoy the result. Personally, I managed to export this beauty only to PDF, however, the Cyrillic alphabet disappears, so if your page has Russian, add the " &lang=en" after " &v=5.16" to the VK function . My result looks somehow so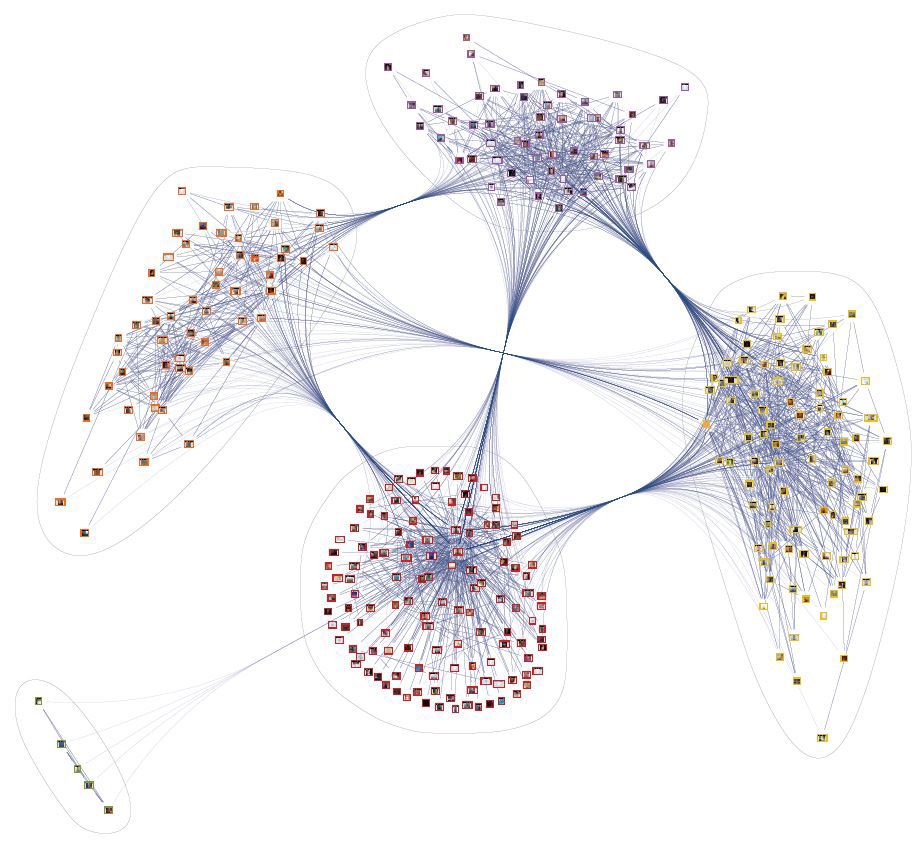




impressive. Globally. Especially when contact is the main means of communication.

Notepad download here . More than 300 people in one request no longer pass, it is necessary to share about this further.

---

(a week passed)

Today they proved to me that drawing yourself on a graph is useless, because in any case you are connected with each of your friends by one connection. Therefore, this connection is redundant. I rebuilt my graphs and they changed. Also, I added a mechanism to automatically split the friends list into parts and collect the result. Now it even shows the progress of execution - after each request, it prints a line and when there are as many printed lines as there are parts in the divided list of friends, this is 100%.



It was experimentally determined that if there are more than 200 people in one request, problems begin. The optimal quantity is 100. In general, the smaller the more reliable. I have 50 because there are 300 friends in total.

And yet, I had to throw out of friends all those with whom I did not have in common. They are carefully displayed and excluded from further calculations.

All this is available here.