The task of changing the voice. Part 2. Physical / acoustic approach to speech presentation
In this post we continue a series of articles devoted to the problem of analyzing and changing a person’s voice. Let us briefly recall the contents of the previous article :
- the sound composition of speech was briefly described
- important processes such as phonation and articulation were described
- a weak classification of the sounds of human speech was given and the characteristic features of the classes of sounds
were described - problems arising from the processing of speech signals were briefly identified
We also outlined the tasks that our division in the i-Free company actually solves. The previous article ended with a “loud” promise to describe the presentation patterns of the speech signal and show how these models can be used to change the voice of the speaker.
Here we immediately make a small reservation. The term “speech signal” can be understood in different ways and often the meaning depends on the context. In the context of our work, we are only interested in the sound-acoustic properties of a speech signal, its semantic and emotional load will not be considered in this and the next articles.
With a creative approach to the task of changing the voice, most of the known models for representing the speech signal are a very powerful tool that allows you to do very, very much. It does not seem expedient to classify such undertakings somehow, and a lot of time will be spent on demonstrating “everything in a row”. In this and the next article, we restrict ourselves to only a brief description of the most commonly used models and somehow try to explain their physical / practical meaning. Examples of the application of these models will be shown a little later - in the following articles we will describe the simplest implementation of effects such as changes in the gender and age of the speaker.
WARNING!

This article aims to describe just a little bit the physics of the formation of sound in the speech path using a simplified model. As a result, the article contains a number of formulas and, possibly, not quite obvious transitions. The primary sources are indicated in the text and, if desired, you can familiarize yourself with this material in more detail yourself. The models described in this article are rarely used for practical tasks of processing recorded speech, rather for research. A reader who is interested only in applied speech signal presentation models will be able to gather information for himself in our next article.
In order to change the properties of any signal, its precise description is not always required. Such operations as amplification, filtering, resampling (changing the sampling frequency), compression , and clipping can very well be done if there is only approximate knowledge about the processed signal. With regard to the task of processing sound, such operations can be attributed to the most basic. Their use, with the exception of “extreme” cases, as a rule does not significantly affect the perception of the processed sound. Really interesting effects with their help are very difficult to obtain, and beyond recognition, spoiling the signal with immense application is as easy as shelling pears.
It’s possible to apply some more cunning transformations, for example modulation and delay (with direct and feedback). Such well-known effects as flanger, tremolo / vibrato, chorus, phaser, wah-wah, comb filter and many others are built on these transformations and can very well be applied not only to musical instruments, but also to the voice. More details about these effects and their implementation can be found in the literature at the end of the subclause. As mentioned in the first article, these effects give the voice a very unusual sound, but the result will not be perceived by ear as natural.
When you want to change the voice so that the result remains “human”, the “thoughtless” conversion of the input signal will not work. A more successful approach to such a task is the analysis of the signal, changing its parameters and the subsequent reconstruction of the new signal, the “rough” scheme for implementing the approach is shown below:
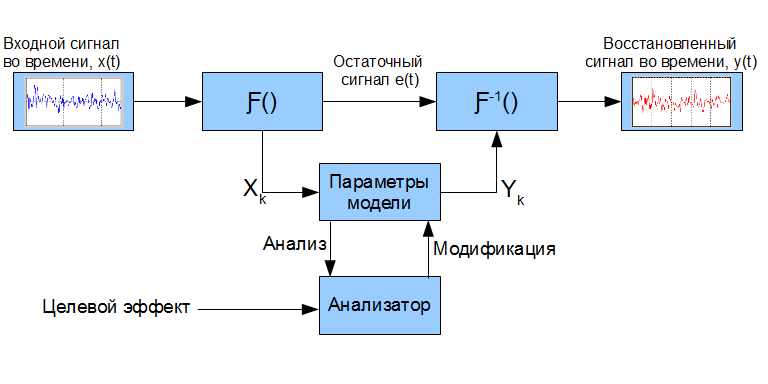
The symbol Ƒ () denotes a transformation that maps the input signal (or part of it) to a certain set of parameters Xk that describe certain properties of the signal. Ƒ ^ -1 () denotes the inverse transformation from the parametric representation to the time domain, actually “resynthesis” *. Some models describe only the most important signal properties from the point of view of this model, and so-called signal-error - e (t). Its meaning is the difference between the input signal and the signal synthesized using the applied model, provided that the parametric representation of the signal is not modified (e (t) = y (t) - x (t) | X_k = Y_k) **, examples will be given further. Having a parametric representation of the signal, it is possible to perform its more versatile analysis and modify certain parameters,
When analyzing a speech signal, it is always necessary to remember about its property to vary greatly even over very short time intervals. Models that use time integration operations in their calculation, thus, can adequately describe the speech signal only at short time intervals. This directly implies the need for signal processing using similar models in small portions. Therefore, in the process of resynthesis, it is necessary to pay special attention to “gluing seams” so that short synthesized signal fragments smoothly (without “clicks”) flow one into another.
* - the operator ^ will further denote exponentiation, i.e., k ^ n is the exponentiation of k to the power n.
** - underline will further symbolically denote subscript indexing
_______________________
Promised literature describing the “internal” structure of many sound effects:
The Theory and Technique of Electronic Music (Miller Puckette)
DAFX - Digital Audio Effects (edited by Udo Zolzer)
Introduction To Digital Signal Processing - Computer Musically Speaking (Tae Hong Park)
It’s worth starting a conversation about speech signal models with the model, so to speak, of the “lowest” level - the acoustic speech signal model. Looking ahead, we’ll immediately say that research at this level is close to fundamental science and requires a very serious theoretical base and technical equipment. In our unit, such work is not carried out and here this model is mentioned only for scientific and educational purposes. (The request is not to react sharply to the “boring” references to the literature, their transcripts will be given at the end of the article and the interested reader will be able to independently investigate the issue)
The purpose of the acoustic model is to describe the physiological structure of a particular person’s speech pathway, parameterize the articulation process in time and reflect the influence of these parameters on the air flow passing through the speech path. As a basic work, many authors refer to [1], where M. Portnoff studied the question of approximating a person’s speech tract using a pipe with a non-uniform time-varying cross-sectional area (illustration below).
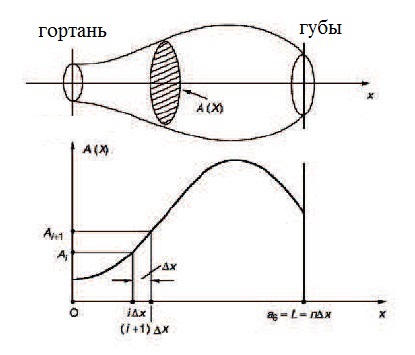
The basic differential equations describing the relationship between pressure and air velocity in a given pipe [2], [3] are presented below. In appearance, they do not seem so “scary” (unless each member of the equation is disclosed in detail):

where p = p (x, t) is the pressure change depending on the time t and the coordinates of the point x in the pipe, u = u (x, t) is the volumetric velocity of the air flow in the pipe, ρ is the air density in the pipe, c is the speed sound, A = A (x, t) is the cross-sectional area of the pipe at point x at time t. The total pipe length is l.
These equations do not have an algebraic solution, except for the simplest cases with strict restrictions on the initial / final conditions [3]. To find numerical solutions, it is necessary to obtain the values of pressure and air velocity at the initial and final points of the vocal tract - the larynx and lips, respectively. Nevertheless, the uncertainty of the values of the function A (x, t) remains a big problem. As stated in [4], advances in the field of three-dimensional tomography allow significant refinement of the relationship between the area of the vocal tract and its acoustic characteristics. However, even knowing fully the behavior of A (x, t), or in the case of its stationarity in time (which is true when analyzing short voiced segments), it is still necessary to make a large number of assumptions in order to obtain some practically useful model. Factors
1) Knowledge of the behavior of A (x, t) in time (unique for each speaker)
2) Losses of sound energy associated with heat transfer and viscous friction in the speech tract
3) Losses associated with the elasticity of the walls of the speech tract (their compliance with incoming air pulses)
4) Emission of sound in the region of the lips
5) The effect of the nasopharynx as an additional resonator / emitter of sound
6) The process of excitation of the initial sound waves (phonation), which is also unique for each individual person
Each of these factors is a separate topic for serious research. If we return to the task of changing the voice using the analysis and resynthesis approach, then to apply this model it is necessary to restore a large number of physiological parameters of the speaker’s speech path from the signal received for processing. Findings of the parameters of the vocal tract and / or articulation parameters from the existing sound signal, experts call the inverse speech problem ([5]). These problems are ill-conditioned and, for their exact solution, require large restrictions on the values of the desired parameters, or their plausible initial approximations, which can be obtained using specialized measurements.
From the point of view of sound processing, obtaining a physically accurate model of a person’s speech pathway and its articulation parameters is of the greatest importance for:
- forensic examination
- medical diagnostics
- speech synthesis systems (text-to-speech systems)
In real-time sound processing, the exact physical Acoustic modeling of sound generation is hardly possible without any a priori knowledge of the speaker’s speech path. For this reason, it is hard to imagine applying this approach to working with unknown voices. Although theoretically, the physical-acoustic approach should, with proper implementation, give the most believable sound, since it is a direct simulation of the processes occurring during sound production.
Having made some assumptions, it is possible to obtain a simplified approximation of the speech path from the model described above, while the frequency response of this approximation is quite close to real measurements. A good description of this simplified model is given in [3]. The main point is given below with emphasis on the implied but not explained in detail in [3] details. The above assumptions come down to the following:
a) For “long” sound waves (whose frequency is less than 4000 Hz, respectively ~ 9 cm or more), it is possible to neglect the turns in the speech tract and present it as an elongated tube (as in the previous figure). Such an approach is close to the analysis of the acoustics of many wind instruments, where only propagation of longitudinal sound waves is considered.
b) It is possible to neglect the losses associated with viscous friction and thermal conductivity. These losses are significantly manifested only in the high-frequency region, and their effect is small in comparison with losses due to sound emission.
c) The losses associated with the elasticity of the walls of the vocal tract are neglected.
d) The radiating surface (mouth and / or nose) is approximated by a hole in a plane, not a sphere.
e) In order to solve differential equations describing the relationship between the space velocity of air and pressure, restrictions are imposed on the boundary conditions:
- the sound source in the larynx (Glottis) u_G (0, t) is not subject to pressure fluctuations in the speech tract,
- pressure at the output of the speech path in the region of the lips (Lips) p_L (l, t) constantly.
f) The cross-sectional area A (x, t) is approximated by a discrete function, see the figure below. The vocal tract thus appears to be a concatenation of pipes of different diameters. At the moment of analysis, it is assumed that A (x, t) is stationary in time, which is true for short time intervals.

To find the frequency response of this system, we need to find the ratio of the frequency response of the signal at the output of the system U_n (w) to the frequency response of the signal at the input of the system U_1 (w). To do this, imagine the input signal as a complex exponent with an arbitrary frequency and some amplitude characteristic (U_G (w) * exp (jwt)). After this, it is necessary to apply equations (1) sequentially for each pipe in the system. At the joints of pipes, it is possible to apply the principle of continuity of the functions u (x, t) and p (x, t) in space. In simpler words:
1) suppose that the 1st and 2nd segments are analyzed
2) the pressure and air volumetric velocity at the very end of the 1st segment should be equal to the pressure and air volumetric velocity at the very beginning of the 2nd segment
3) we get ratios:
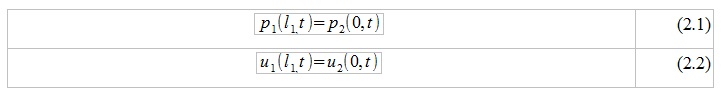
Relations (2) will be valid both for the functions p (x, t) and u (x, t) themselves, and for their frequency characteristics P (x, w) and U (x, w).
The analysis can be carried out both from beginning to end (from the larynx to the lips), and vice versa. The second option is even simpler. For complete happiness it is only necessary to apply the “most marginal” conditions:

The value Z_L (w) is also called the radiation impedance in the case of the analysis of human speech, when the radiating surface is approximated by a small hole on a large plane (condition (d)) can be expressed as a function of frequency and some predefined constants L_L and R_L. The value Z_G (w) is the acoustic impedance in the larynx and can also be calculated using some of the predefined constants L_G and R_G. U_0 (w) is the frequency response of the signal at the larynx outlet, which we conventionally assumed for the frequency analysis of our model to be some complex exponent.
Using solutions for differential equations (1) and applying the condition of pressure continuity and air space velocity in space, it becomes possible to go through the entire “chain” of pipes and express the initial air flow velocity U_G (w) as a function of the final velocity U_L (w) or vice versa:
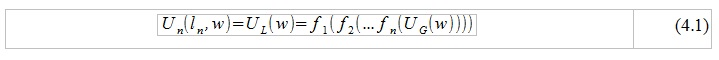
where f_k is a certain function depending both on the solutions of equations (1) for the kth pipe and on the length / area of the kth pipe. After that, it is relatively simple to find the ratio of “entry” to “exit”.
All described steps are valid only under assumptions a) -e). The resulting frequency response, in the presence of an adequate discrete approximation of the vocal tract (A_k and l_k, k = 1: n), acceptable describes the formant characteristics of various vowels and nasal consonants. To describe nasal sounds, the system must become more complicated, because it is necessary to take into account the additional radiating surface and the branching of the speech tract that occurs when the soft palate is lowered.
Losses associated with heat transfer, viscous friction and elasticity of the vocal tract can be adequately taken into account in this model, however, then the basic differential equations will become somewhat more complicated (the form of the function A (x, t) will become more complicated) and the boundary conditions.
To implement sound effects, the use of this model involves the evaluation of the values of A_k and l_k from the processed signal, their modification and the subsequent synthesis of a new sound. To solve the inverse problem of estimating A_k and l_k from the input signal, it is necessary to know the excitation signal that passed through the speech path at the time of analysis, or at least have its plausible approximation. There are a considerable number of models for approximating the excitation signal of a voiced speech fragment, however, for their application it is necessary, in turn, to determine the appropriate model choice and selection of its parameters for the processed signal, which is also not always a trivial task. Again, there are methods that allow, with various kinds of errors, to restore the excitation signal of the speech tract from the processed sound.
Even if there is a good approximation of the excitation signal, finding the values of A_k and l_k requires solving a system of nonlinear equations, which in turn leads to numerical methods and the search for optimal values with all the consequences. The above conceptually (NOT MATHEMATICALLY STRICTLY!) Is depicted in the figure below:
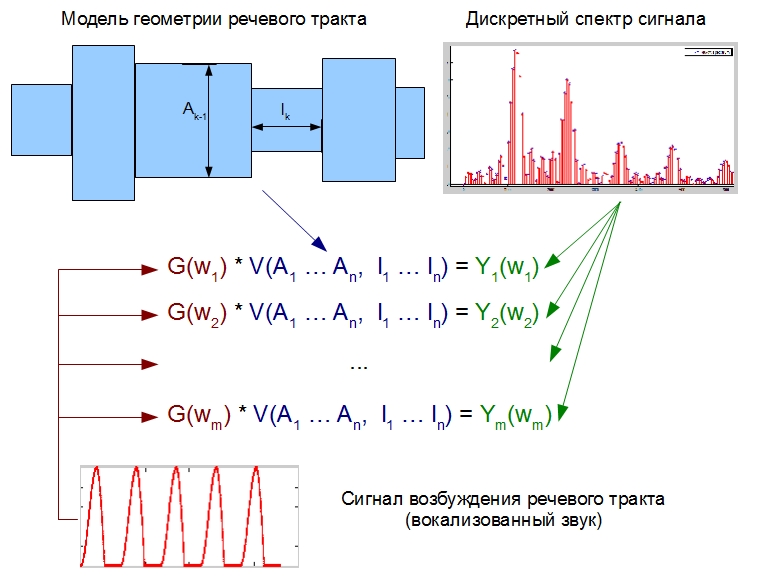
In this figure, Y (w_k) and G (w_k) are the discrete spectrum of the processed signal and its excitation signal, respectively. V (A, I) is a model of the frequency response of the vocal tract, depending on the desired A_k and l_k.
The implementation of a system capable of doing all of the above in the absence of any a priori knowledge of the signal seems to be a rather difficult task. Additional difficulties arise when trying to make such a system work with noisy signals in real time.
In general, it can be concluded that such a model is of greater value for speech synthesis problems (text-to-speech). Analysis of an unknown input signal using a similar model is a very dubious pleasure. There is an alternative view of this model, making it more suitable for "our" goals.
To begin with, we immediately introduce another additional restriction on the model considered in the previous paragraph:
All the lengths of the pipes that make up the vocal tract are taken equal to each other:
l_1 = l_2 = ... = l_n = LEN
Next, you should turn to the acoustic of the pipes and remember that longitudinal sound waves tend to bounce off the open end of the pipe. In other words, the function of the air velocity is the function of two propagating in different directions of the air “waves”: u (t, x) = f (u + (t, x), u- (t, x)). By indices + and - we will denote sound waves going in the forward (from the larynx to the lips) and in the opposite directions, respectively. The foregoing is schematically illustrated below:
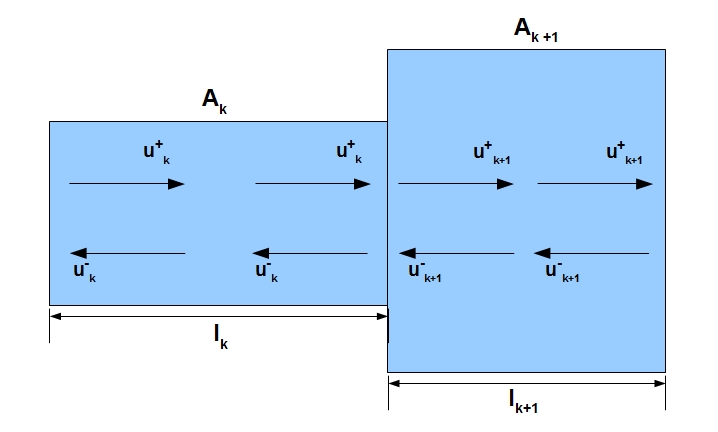
It is important to remember that this is just a diagram. In fact, the sound does not move forward along the top and back along the bottom of the pipe. To at least somehow imagine how this actually happens, you can turn to a wonderful illustration from cnx.org, which depicts a standing acoustic wave in an ideal tube.
The aforesaid is also confirmed by the fact that equations (1) have general solutions of the form:

Recall that ρ is the air density in the pipe, c is the speed of sound, A = A (x, t) is the cross-sectional area of the pipe at point x at time t. u + (x, t) is the space velocity of the air going in the forward direction, u- (x, t) is in the opposite direction.
As stated in [3], these solutions can be derived by applying the theory of analysis of electrical circuits, if we allow an analogy: pressure p voltage in the circuit U; air volumetric velocity u current in circuit I; acoustic inductance ρ / A inductance L; acoustic capacity A / (ρc ^ 2) capacity C.
Equations (5) are valid for each tube that makes up our approximation of the speech tract. Now, knowing the general form of the solutions of equations (1), we apply the condition of continuity of pressure and air velocity in space and, denoting by k the index of the analyzed pipe, we can say that
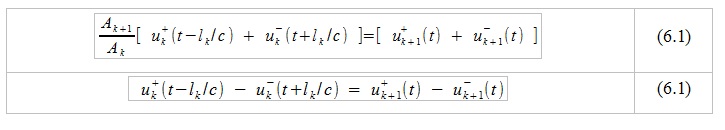
Having made a number of algebraic transformations (for details, refer to [3]), it is possible to show that:
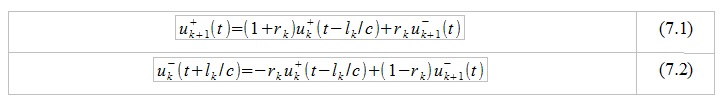
The coefficient r_k in this system is called the reflection coefficient, its numerical value can be expressed as:

The value l_k / c, often found in equations (6), (7), is numerically equal to the time required for the air to go through the kth pipe. Since in the current system under analysis all the pipe lengths are equal to LEN, we denote by τ the time required by the air to travel the distance LEN.
In such a cunning way, we obtained relations (7) reflecting the relationship between the space velocity of the forward / reverse air flows in two adjacent pipes. We show these relationships graphically:
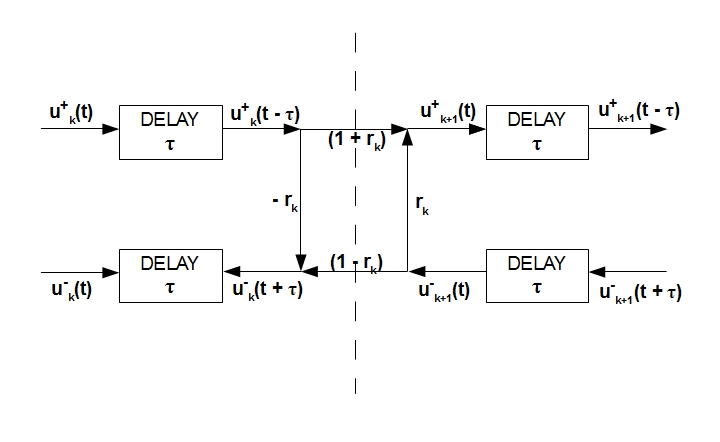
The main conclusion is that the direct / reverse air flows in adjacent pipes are directly interconnected through the areas of these pipes (coefficient r_k).
In the transition from continuous time t to discrete, each signal sample follows another after a certain sampling period T_s. It is possible to select the number of pipes in our system so that each delay τ in the figure above corresponds to one sampling period. To do this, consider a simple example. If we take the value of the speed of sound at 350 m / s and the average length of the human speech path at 0.175 m (17.5 cm), we can say that the sound wave will pass the entire path without reflections in 0.0005 sec. Suppose our system consists of 10 pipes. Then the delay τ in each pipe will be about 0.00005 sec. If we want, for example, that this delay corresponds to our sampling period Ts, then we get the required sampling frequency for this signal: F_s = 1 / T_s = 20 kHz. In practice, it is also possible to solve the inverse problem - the number of pipes for approximating the speech tract is “adjusted” to the sampling frequency of the existing signal and the conditions for its recording (for example, taking into account the dependence of air speed on temperature). Depending on the permissible complexity of the system, there may be a strict restriction on the acceptable number of pipes in the system. As shown in [3], for analyzing such a system in discrete time, it is quite convenient to choose a sampling period equal to 2τ, since all re-reflected air pulses reach the system output at times multiple of 2τ. You can get rid of the “intermediate” delays of half a count that occur with this approach if all delays in one of the signal propagation directions (forward or reverse) are transferred in the opposite direction. We will not give the proof in order to save space; more details about this can be found again in [3]. Recalling from the theory of analysis of discrete systems that:
- the transfer function of the system is usually expressed through the Z-transformation
- the operator of multiplication by z ^ (- 1) corresponds to the delay of the signal by one sample,
we can ultimately depict the voice path, for example, consisting of 3 pipes in the following relatively simple way:
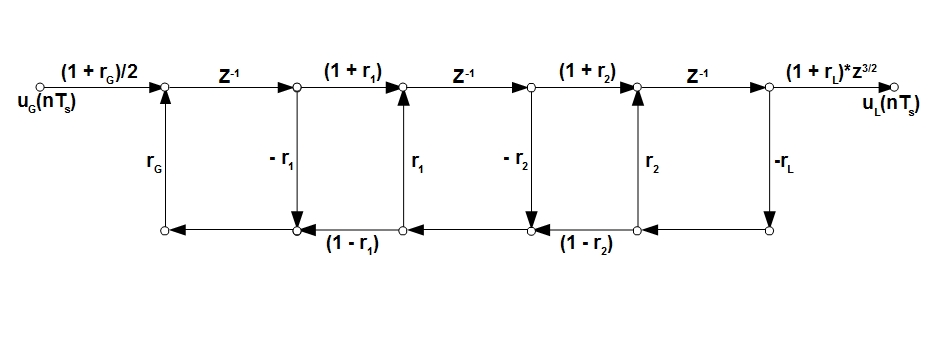
Initial and final coefficients reflections are taken from the boundary conditions (3). A detailed transition from equations (3) to the form (1 + r_G) / 2 and (1 + r_L) is also omitted here for brevity. The multiplier z ^ (3/2) was added just to compensate for the transfer of all intermediate delays of signal propagation from the reverse "branch" to the straight line - 3 delays in z ^ (- 1/2) were transferred from the lower "branch" to the upper one and to compensate for this action factor z ^ (3/2) is applied.
The transition from the “analog” system from the previous paragraph to the digital system allows us to significantly simplify the equations describing the system and instead of differential equations (1) to use relatively simple difference equations similar to (7), only time t will turn into a discrete index of the signal in them. When working with an unknown signal, the desired parameters of this model are only the area of the pipes that make up the voice path - A_k. The system of equations used to search for A_k cannot be completely reduced to a linear one, however its general form will be simpler than the form of a similar system from the previous paragraph (a figure with a diagram of finding the areas and lengths of the speech path from the system of equations).
Having made a number of assumptions, we can say that the general frequency characteristic of the speech tract in the Z-region looks like ([2], [3]):
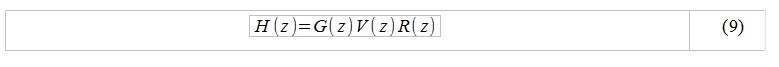
where G (z) is the frequency characteristic of the air flow in the larynx, V (z) is the frequency the characteristic of the vocal tract (most of all depends on A (x, t)), R (z) is the frequency response of the sound emitter in the region of the lips.
In speech modeling problems, G (z) and R (z) are usually approximated to the extent of simplified models (especially R (z), which is often represented by a simple differentiator). V (z) is the most often sought-after member and this article was devoted to him. In some problems, it is required to estimate G (z) as accurately as possible, since This member is responsible for sound phonation and is determined by the physical parameters of the larynx of a particular person. Perhaps a separate article will be written about the analysis of G (z) later.
Having at its disposal only voice recording, it is unlikely that today any of the tasks mentioned above can be solved algebraically accurately - it is only possible to use numerical methods to find the optimal values. Having obtained approximate values of the necessary parameters, depending on the desired sound effect, these parameters are modified, after which a new sound can be synthesized.
The approaches to the analysis of speech signals described in this article are more applicable to text-to-speech speech synthesis problems. However, with high-quality voice recording and some a priori knowledge, it is possible to apply these models to “our” tasks.
In the next article we will talk about more applied and possibly more understandable models for representing a speech signal, namely:
- LPC (direct “descendant” of the approach described in this article)
- Harmonic speech signal model (phase vocoder)
- HPN model
________________________
Primary sources:
[1] MR Portnoff, A Quasi-One-Dimensional Digital Simulation for Time-Varying Vocal Tract
[ 2] NR Raajan, TR Sivaramakrishnan and Y. Venkatramani, Mathematical Modeling of Speech Production and Its Application to Noise Cancellation (Chapter 3 from Speech Enhancement, Modeling and Recognition - Algorithms and Applications)
[3] LR Rabiner, RW Schafer, Digital Processing of Speech Signals
[4] V. N. Sorokin, Fundamental research on speech and applied problems of speech technologies
[5] V.N. Sorokin, I.S. Makarov, The inverse problem for a voice source.
- the sound composition of speech was briefly described
- important processes such as phonation and articulation were described
- a weak classification of the sounds of human speech was given and the characteristic features of the classes of sounds
were described - problems arising from the processing of speech signals were briefly identified
We also outlined the tasks that our division in the i-Free company actually solves. The previous article ended with a “loud” promise to describe the presentation patterns of the speech signal and show how these models can be used to change the voice of the speaker.
Here we immediately make a small reservation. The term “speech signal” can be understood in different ways and often the meaning depends on the context. In the context of our work, we are only interested in the sound-acoustic properties of a speech signal, its semantic and emotional load will not be considered in this and the next articles.
With a creative approach to the task of changing the voice, most of the known models for representing the speech signal are a very powerful tool that allows you to do very, very much. It does not seem expedient to classify such undertakings somehow, and a lot of time will be spent on demonstrating “everything in a row”. In this and the next article, we restrict ourselves to only a brief description of the most commonly used models and somehow try to explain their physical / practical meaning. Examples of the application of these models will be shown a little later - in the following articles we will describe the simplest implementation of effects such as changes in the gender and age of the speaker.
WARNING!

This article aims to describe just a little bit the physics of the formation of sound in the speech path using a simplified model. As a result, the article contains a number of formulas and, possibly, not quite obvious transitions. The primary sources are indicated in the text and, if desired, you can familiarize yourself with this material in more detail yourself. The models described in this article are rarely used for practical tasks of processing recorded speech, rather for research. A reader who is interested only in applied speech signal presentation models will be able to gather information for himself in our next article.
Sound special effects and why are models of speech signal representation needed?
In order to change the properties of any signal, its precise description is not always required. Such operations as amplification, filtering, resampling (changing the sampling frequency), compression , and clipping can very well be done if there is only approximate knowledge about the processed signal. With regard to the task of processing sound, such operations can be attributed to the most basic. Their use, with the exception of “extreme” cases, as a rule does not significantly affect the perception of the processed sound. Really interesting effects with their help are very difficult to obtain, and beyond recognition, spoiling the signal with immense application is as easy as shelling pears.
It’s possible to apply some more cunning transformations, for example modulation and delay (with direct and feedback). Such well-known effects as flanger, tremolo / vibrato, chorus, phaser, wah-wah, comb filter and many others are built on these transformations and can very well be applied not only to musical instruments, but also to the voice. More details about these effects and their implementation can be found in the literature at the end of the subclause. As mentioned in the first article, these effects give the voice a very unusual sound, but the result will not be perceived by ear as natural.
When you want to change the voice so that the result remains “human”, the “thoughtless” conversion of the input signal will not work. A more successful approach to such a task is the analysis of the signal, changing its parameters and the subsequent reconstruction of the new signal, the “rough” scheme for implementing the approach is shown below:

The symbol Ƒ () denotes a transformation that maps the input signal (or part of it) to a certain set of parameters Xk that describe certain properties of the signal. Ƒ ^ -1 () denotes the inverse transformation from the parametric representation to the time domain, actually “resynthesis” *. Some models describe only the most important signal properties from the point of view of this model, and so-called signal-error - e (t). Its meaning is the difference between the input signal and the signal synthesized using the applied model, provided that the parametric representation of the signal is not modified (e (t) = y (t) - x (t) | X_k = Y_k) **, examples will be given further. Having a parametric representation of the signal, it is possible to perform its more versatile analysis and modify certain parameters,
When analyzing a speech signal, it is always necessary to remember about its property to vary greatly even over very short time intervals. Models that use time integration operations in their calculation, thus, can adequately describe the speech signal only at short time intervals. This directly implies the need for signal processing using similar models in small portions. Therefore, in the process of resynthesis, it is necessary to pay special attention to “gluing seams” so that short synthesized signal fragments smoothly (without “clicks”) flow one into another.
* - the operator ^ will further denote exponentiation, i.e., k ^ n is the exponentiation of k to the power n.
** - underline will further symbolically denote subscript indexing
_______________________
Promised literature describing the “internal” structure of many sound effects:
The Theory and Technique of Electronic Music (Miller Puckette)
DAFX - Digital Audio Effects (edited by Udo Zolzer)
Introduction To Digital Signal Processing - Computer Musically Speaking (Tae Hong Park)
Physical modeling of sound production in speech. Acoustic model of the vocal tract.
It’s worth starting a conversation about speech signal models with the model, so to speak, of the “lowest” level - the acoustic speech signal model. Looking ahead, we’ll immediately say that research at this level is close to fundamental science and requires a very serious theoretical base and technical equipment. In our unit, such work is not carried out and here this model is mentioned only for scientific and educational purposes. (The request is not to react sharply to the “boring” references to the literature, their transcripts will be given at the end of the article and the interested reader will be able to independently investigate the issue)
The purpose of the acoustic model is to describe the physiological structure of a particular person’s speech pathway, parameterize the articulation process in time and reflect the influence of these parameters on the air flow passing through the speech path. As a basic work, many authors refer to [1], where M. Portnoff studied the question of approximating a person’s speech tract using a pipe with a non-uniform time-varying cross-sectional area (illustration below).

The basic differential equations describing the relationship between pressure and air velocity in a given pipe [2], [3] are presented below. In appearance, they do not seem so “scary” (unless each member of the equation is disclosed in detail):

where p = p (x, t) is the pressure change depending on the time t and the coordinates of the point x in the pipe, u = u (x, t) is the volumetric velocity of the air flow in the pipe, ρ is the air density in the pipe, c is the speed sound, A = A (x, t) is the cross-sectional area of the pipe at point x at time t. The total pipe length is l.
These equations do not have an algebraic solution, except for the simplest cases with strict restrictions on the initial / final conditions [3]. To find numerical solutions, it is necessary to obtain the values of pressure and air velocity at the initial and final points of the vocal tract - the larynx and lips, respectively. Nevertheless, the uncertainty of the values of the function A (x, t) remains a big problem. As stated in [4], advances in the field of three-dimensional tomography allow significant refinement of the relationship between the area of the vocal tract and its acoustic characteristics. However, even knowing fully the behavior of A (x, t), or in the case of its stationarity in time (which is true when analyzing short voiced segments), it is still necessary to make a large number of assumptions in order to obtain some practically useful model. Factors
1) Knowledge of the behavior of A (x, t) in time (unique for each speaker)
2) Losses of sound energy associated with heat transfer and viscous friction in the speech tract
3) Losses associated with the elasticity of the walls of the speech tract (their compliance with incoming air pulses)
4) Emission of sound in the region of the lips
5) The effect of the nasopharynx as an additional resonator / emitter of sound
6) The process of excitation of the initial sound waves (phonation), which is also unique for each individual person
Each of these factors is a separate topic for serious research. If we return to the task of changing the voice using the analysis and resynthesis approach, then to apply this model it is necessary to restore a large number of physiological parameters of the speaker’s speech path from the signal received for processing. Findings of the parameters of the vocal tract and / or articulation parameters from the existing sound signal, experts call the inverse speech problem ([5]). These problems are ill-conditioned and, for their exact solution, require large restrictions on the values of the desired parameters, or their plausible initial approximations, which can be obtained using specialized measurements.
From the point of view of sound processing, obtaining a physically accurate model of a person’s speech pathway and its articulation parameters is of the greatest importance for:
- forensic examination
- medical diagnostics
- speech synthesis systems (text-to-speech systems)
In real-time sound processing, the exact physical Acoustic modeling of sound generation is hardly possible without any a priori knowledge of the speaker’s speech path. For this reason, it is hard to imagine applying this approach to working with unknown voices. Although theoretically, the physical-acoustic approach should, with proper implementation, give the most believable sound, since it is a direct simulation of the processes occurring during sound production.
More mundane approach. Simplified acoustic model of the speech tract.
Having made some assumptions, it is possible to obtain a simplified approximation of the speech path from the model described above, while the frequency response of this approximation is quite close to real measurements. A good description of this simplified model is given in [3]. The main point is given below with emphasis on the implied but not explained in detail in [3] details. The above assumptions come down to the following:
a) For “long” sound waves (whose frequency is less than 4000 Hz, respectively ~ 9 cm or more), it is possible to neglect the turns in the speech tract and present it as an elongated tube (as in the previous figure). Such an approach is close to the analysis of the acoustics of many wind instruments, where only propagation of longitudinal sound waves is considered.
b) It is possible to neglect the losses associated with viscous friction and thermal conductivity. These losses are significantly manifested only in the high-frequency region, and their effect is small in comparison with losses due to sound emission.
c) The losses associated with the elasticity of the walls of the vocal tract are neglected.
d) The radiating surface (mouth and / or nose) is approximated by a hole in a plane, not a sphere.
e) In order to solve differential equations describing the relationship between the space velocity of air and pressure, restrictions are imposed on the boundary conditions:
- the sound source in the larynx (Glottis) u_G (0, t) is not subject to pressure fluctuations in the speech tract,
- pressure at the output of the speech path in the region of the lips (Lips) p_L (l, t) constantly.
f) The cross-sectional area A (x, t) is approximated by a discrete function, see the figure below. The vocal tract thus appears to be a concatenation of pipes of different diameters. At the moment of analysis, it is assumed that A (x, t) is stationary in time, which is true for short time intervals.

To find the frequency response of this system, we need to find the ratio of the frequency response of the signal at the output of the system U_n (w) to the frequency response of the signal at the input of the system U_1 (w). To do this, imagine the input signal as a complex exponent with an arbitrary frequency and some amplitude characteristic (U_G (w) * exp (jwt)). After this, it is necessary to apply equations (1) sequentially for each pipe in the system. At the joints of pipes, it is possible to apply the principle of continuity of the functions u (x, t) and p (x, t) in space. In simpler words:
1) suppose that the 1st and 2nd segments are analyzed
2) the pressure and air volumetric velocity at the very end of the 1st segment should be equal to the pressure and air volumetric velocity at the very beginning of the 2nd segment
3) we get ratios:
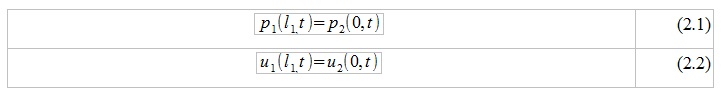
Relations (2) will be valid both for the functions p (x, t) and u (x, t) themselves, and for their frequency characteristics P (x, w) and U (x, w).
The analysis can be carried out both from beginning to end (from the larynx to the lips), and vice versa. The second option is even simpler. For complete happiness it is only necessary to apply the “most marginal” conditions:

The value Z_L (w) is also called the radiation impedance in the case of the analysis of human speech, when the radiating surface is approximated by a small hole on a large plane (condition (d)) can be expressed as a function of frequency and some predefined constants L_L and R_L. The value Z_G (w) is the acoustic impedance in the larynx and can also be calculated using some of the predefined constants L_G and R_G. U_0 (w) is the frequency response of the signal at the larynx outlet, which we conventionally assumed for the frequency analysis of our model to be some complex exponent.
Using solutions for differential equations (1) and applying the condition of pressure continuity and air space velocity in space, it becomes possible to go through the entire “chain” of pipes and express the initial air flow velocity U_G (w) as a function of the final velocity U_L (w) or vice versa:
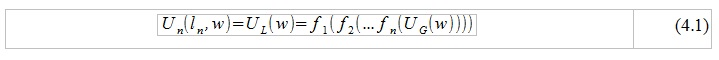
where f_k is a certain function depending both on the solutions of equations (1) for the kth pipe and on the length / area of the kth pipe. After that, it is relatively simple to find the ratio of “entry” to “exit”.
All described steps are valid only under assumptions a) -e). The resulting frequency response, in the presence of an adequate discrete approximation of the vocal tract (A_k and l_k, k = 1: n), acceptable describes the formant characteristics of various vowels and nasal consonants. To describe nasal sounds, the system must become more complicated, because it is necessary to take into account the additional radiating surface and the branching of the speech tract that occurs when the soft palate is lowered.
Losses associated with heat transfer, viscous friction and elasticity of the vocal tract can be adequately taken into account in this model, however, then the basic differential equations will become somewhat more complicated (the form of the function A (x, t) will become more complicated) and the boundary conditions.
To implement sound effects, the use of this model involves the evaluation of the values of A_k and l_k from the processed signal, their modification and the subsequent synthesis of a new sound. To solve the inverse problem of estimating A_k and l_k from the input signal, it is necessary to know the excitation signal that passed through the speech path at the time of analysis, or at least have its plausible approximation. There are a considerable number of models for approximating the excitation signal of a voiced speech fragment, however, for their application it is necessary, in turn, to determine the appropriate model choice and selection of its parameters for the processed signal, which is also not always a trivial task. Again, there are methods that allow, with various kinds of errors, to restore the excitation signal of the speech tract from the processed sound.
Even if there is a good approximation of the excitation signal, finding the values of A_k and l_k requires solving a system of nonlinear equations, which in turn leads to numerical methods and the search for optimal values with all the consequences. The above conceptually (NOT MATHEMATICALLY STRICTLY!) Is depicted in the figure below:

In this figure, Y (w_k) and G (w_k) are the discrete spectrum of the processed signal and its excitation signal, respectively. V (A, I) is a model of the frequency response of the vocal tract, depending on the desired A_k and l_k.
The implementation of a system capable of doing all of the above in the absence of any a priori knowledge of the signal seems to be a rather difficult task. Additional difficulties arise when trying to make such a system work with noisy signals in real time.
In general, it can be concluded that such a model is of greater value for speech synthesis problems (text-to-speech). Analysis of an unknown input signal using a similar model is a very dubious pleasure. There is an alternative view of this model, making it more suitable for "our" goals.
The speech path as a discrete filter
To begin with, we immediately introduce another additional restriction on the model considered in the previous paragraph:
All the lengths of the pipes that make up the vocal tract are taken equal to each other:
l_1 = l_2 = ... = l_n = LEN
Next, you should turn to the acoustic of the pipes and remember that longitudinal sound waves tend to bounce off the open end of the pipe. In other words, the function of the air velocity is the function of two propagating in different directions of the air “waves”: u (t, x) = f (u + (t, x), u- (t, x)). By indices + and - we will denote sound waves going in the forward (from the larynx to the lips) and in the opposite directions, respectively. The foregoing is schematically illustrated below:

It is important to remember that this is just a diagram. In fact, the sound does not move forward along the top and back along the bottom of the pipe. To at least somehow imagine how this actually happens, you can turn to a wonderful illustration from cnx.org, which depicts a standing acoustic wave in an ideal tube.
The aforesaid is also confirmed by the fact that equations (1) have general solutions of the form:

Recall that ρ is the air density in the pipe, c is the speed of sound, A = A (x, t) is the cross-sectional area of the pipe at point x at time t. u + (x, t) is the space velocity of the air going in the forward direction, u- (x, t) is in the opposite direction.
As stated in [3], these solutions can be derived by applying the theory of analysis of electrical circuits, if we allow an analogy: pressure p voltage in the circuit U; air volumetric velocity u current in circuit I; acoustic inductance ρ / A inductance L; acoustic capacity A / (ρc ^ 2) capacity C.
Equations (5) are valid for each tube that makes up our approximation of the speech tract. Now, knowing the general form of the solutions of equations (1), we apply the condition of continuity of pressure and air velocity in space and, denoting by k the index of the analyzed pipe, we can say that
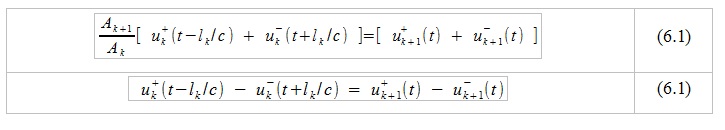
Having made a number of algebraic transformations (for details, refer to [3]), it is possible to show that:
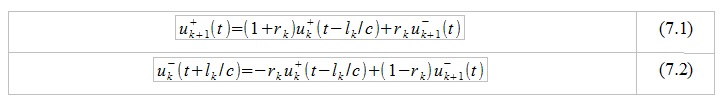
The coefficient r_k in this system is called the reflection coefficient, its numerical value can be expressed as:

The value l_k / c, often found in equations (6), (7), is numerically equal to the time required for the air to go through the kth pipe. Since in the current system under analysis all the pipe lengths are equal to LEN, we denote by τ the time required by the air to travel the distance LEN.
In such a cunning way, we obtained relations (7) reflecting the relationship between the space velocity of the forward / reverse air flows in two adjacent pipes. We show these relationships graphically:

The main conclusion is that the direct / reverse air flows in adjacent pipes are directly interconnected through the areas of these pipes (coefficient r_k).
In the transition from continuous time t to discrete, each signal sample follows another after a certain sampling period T_s. It is possible to select the number of pipes in our system so that each delay τ in the figure above corresponds to one sampling period. To do this, consider a simple example. If we take the value of the speed of sound at 350 m / s and the average length of the human speech path at 0.175 m (17.5 cm), we can say that the sound wave will pass the entire path without reflections in 0.0005 sec. Suppose our system consists of 10 pipes. Then the delay τ in each pipe will be about 0.00005 sec. If we want, for example, that this delay corresponds to our sampling period Ts, then we get the required sampling frequency for this signal: F_s = 1 / T_s = 20 kHz. In practice, it is also possible to solve the inverse problem - the number of pipes for approximating the speech tract is “adjusted” to the sampling frequency of the existing signal and the conditions for its recording (for example, taking into account the dependence of air speed on temperature). Depending on the permissible complexity of the system, there may be a strict restriction on the acceptable number of pipes in the system. As shown in [3], for analyzing such a system in discrete time, it is quite convenient to choose a sampling period equal to 2τ, since all re-reflected air pulses reach the system output at times multiple of 2τ. You can get rid of the “intermediate” delays of half a count that occur with this approach if all delays in one of the signal propagation directions (forward or reverse) are transferred in the opposite direction. We will not give the proof in order to save space; more details about this can be found again in [3]. Recalling from the theory of analysis of discrete systems that:
- the transfer function of the system is usually expressed through the Z-transformation
- the operator of multiplication by z ^ (- 1) corresponds to the delay of the signal by one sample,
we can ultimately depict the voice path, for example, consisting of 3 pipes in the following relatively simple way:

Initial and final coefficients reflections are taken from the boundary conditions (3). A detailed transition from equations (3) to the form (1 + r_G) / 2 and (1 + r_L) is also omitted here for brevity. The multiplier z ^ (3/2) was added just to compensate for the transfer of all intermediate delays of signal propagation from the reverse "branch" to the straight line - 3 delays in z ^ (- 1/2) were transferred from the lower "branch" to the upper one and to compensate for this action factor z ^ (3/2) is applied.
The transition from the “analog” system from the previous paragraph to the digital system allows us to significantly simplify the equations describing the system and instead of differential equations (1) to use relatively simple difference equations similar to (7), only time t will turn into a discrete index of the signal in them. When working with an unknown signal, the desired parameters of this model are only the area of the pipes that make up the voice path - A_k. The system of equations used to search for A_k cannot be completely reduced to a linear one, however its general form will be simpler than the form of a similar system from the previous paragraph (a figure with a diagram of finding the areas and lengths of the speech path from the system of equations).
conclusions
Having made a number of assumptions, we can say that the general frequency characteristic of the speech tract in the Z-region looks like ([2], [3]):
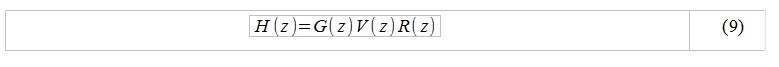
where G (z) is the frequency characteristic of the air flow in the larynx, V (z) is the frequency the characteristic of the vocal tract (most of all depends on A (x, t)), R (z) is the frequency response of the sound emitter in the region of the lips.
In speech modeling problems, G (z) and R (z) are usually approximated to the extent of simplified models (especially R (z), which is often represented by a simple differentiator). V (z) is the most often sought-after member and this article was devoted to him. In some problems, it is required to estimate G (z) as accurately as possible, since This member is responsible for sound phonation and is determined by the physical parameters of the larynx of a particular person. Perhaps a separate article will be written about the analysis of G (z) later.
Having at its disposal only voice recording, it is unlikely that today any of the tasks mentioned above can be solved algebraically accurately - it is only possible to use numerical methods to find the optimal values. Having obtained approximate values of the necessary parameters, depending on the desired sound effect, these parameters are modified, after which a new sound can be synthesized.
The approaches to the analysis of speech signals described in this article are more applicable to text-to-speech speech synthesis problems. However, with high-quality voice recording and some a priori knowledge, it is possible to apply these models to “our” tasks.
In the next article we will talk about more applied and possibly more understandable models for representing a speech signal, namely:
- LPC (direct “descendant” of the approach described in this article)
- Harmonic speech signal model (phase vocoder)
- HPN model
________________________
Primary sources:
[1] MR Portnoff, A Quasi-One-Dimensional Digital Simulation for Time-Varying Vocal Tract
[ 2] NR Raajan, TR Sivaramakrishnan and Y. Venkatramani, Mathematical Modeling of Speech Production and Its Application to Noise Cancellation (Chapter 3 from Speech Enhancement, Modeling and Recognition - Algorithms and Applications)
[3] LR Rabiner, RW Schafer, Digital Processing of Speech Signals
[4] V. N. Sorokin, Fundamental research on speech and applied problems of speech technologies
[5] V.N. Sorokin, I.S. Makarov, The inverse problem for a voice source.
