Satchel problem and Gray code
Not so long ago on Habré there was an article " Gray codes and tasks of search ". This article is more mathematical, rather than programmatic, and it was unbearably hard for me, as a simple programmer, to read it. But the topic itself is familiar to me, so I decided to describe it with my own eyes, as well as talk about how I used it in solving the knapsack problem.

KDPV: a satchel problem on a living example
It all started 10 years ago when I was in ninth grade. I accidentally overheard the conversation of a computer science teacher telling a puzzle to one of the elders: a set of numbers was given, and another number was a control one. It is necessary to find the maximum sum of numbers from the set, which would not exceed the control number.
The task for some reason sunk into my soul. Having returned home, I quickly drew up a solution: a naive search of all possible amounts with the choice of the best. I got combinations by sorting through all N-bit binary numbers and taking the sums of those initial numbers to which the units correspond. But I regretfully found that with the number of elements starting somewhere around 30, the program runs for a very long time. It is not surprising, because the operating time of such an algorithm is n * 2 n (the number of combinations multiplied by the length of the sum).
5 years later. I managed to finish school and go to university, but this task was still with me. Once, leafing through the book "Algorithmic Tricks for Programmers" (Hacker's Delight / Henry S. Warren Jr.), I came across a description of the Gray code: this is a sequence of binary numbers, each of which differs from the previous one by only one bit. “Stop!” I thought. “That means ... Yes!” This means that in the same problem at each step of the search, you can not calculate the whole amount, but only add or subtract one number. " And I immediately went deep into the study of the topic.
Gray code can be constructed for a number of any bit depth. For one category, it is obvious:
0
1
To add a second category, you can add the same backward to this sequence
0
1
1
0
and add units to the second half:
00
01
11
10
Similarly for three categories:
000
001
011
010
110
111
101
100
Such a code, obtained by reflection of a code of lower bit capacity, is called a reflex (reflected) Gray code. There are other sequences, but in practice this is usually used.
This code is named after Frank Gray., which invented the tube ADC, which produced a digital signal in this code. With small changes in the input signal level, the digital output could change in only one bit, and this avoided sudden jumps due to non-simultaneous switching of bits.
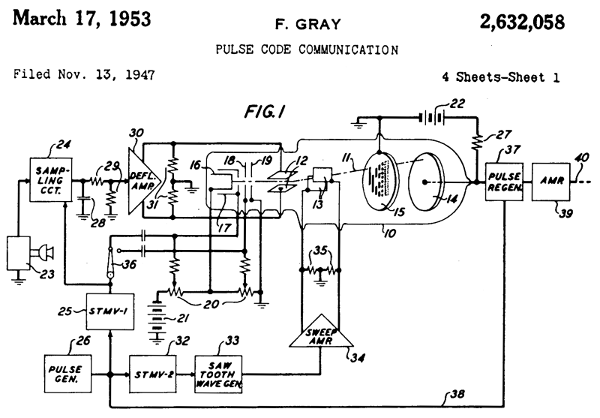
Frank Gray Patent Illustration
The most obvious use of the Gray code is in angle sensors. A sensor similar to what was in old mechanical mice, but determining not the relative displacement, but the absolute value of the angle. For this, for each sensor, several optocouplers and several slotted gratings are needed. Moreover, each subsequent position of the sensor should differ from the previous one only in the state of one bit, otherwise at the borders non-synchronous switching of bits is possible, and, consequently, sharp jumps in the readings of the device. Here you can see a curious feature of the Gray code: the last number also differs from the first one by one bit, so it can be “looped”.

Sensor of absolute angle of rotation. Optical slots are arranged according to the Gray code.
But back to the knapsack problem. The standard formula gives us the Gray code by number:
According to it, we can only calculate the sum of all the necessary elements. And we were going to add or subtract one value at each iteration, right? So, we need to get the numbers of the modified bits. For multi-digit numbers, these numbers will be like this:
0
1
0
2
0
1
0
3
0
1
0
2
0
1
0
4
...
Does it look like nothing? This is the bit number that we set to unity when we simply list ordinary binary numbers. Or else - the number of the minor unit in a binary number. This operation is called find first set.and on most processors it exists as a separate instruction. Visual C ++ provides this instruction as a _BitScanForward function.
So, now we are ready to write a program that solves the knapsack problem through the Gray code. We formulate the problem as follows:
We will store a bitmask of used things, and add or remove one of them as necessary. To get by with ints, we limit the number of things (and bits used) to thirty-one.
I apologize for the possible roughness; unfortunately, C ++ has long been not my core language.
It really works faster than assembling from scratch all the sums, the difference is already noticeable at 20 numbers, and at 30 I did not wait for the naive algorithm to complete, while the new version is completed in 7 seconds. However, given the exponential complexity, this is by no means small: for 50 numbers, using this algorithm no longer makes sense. Unfortunately, any exact algorithm will not work faster than in 2 n ; faster only an approximate solution is possible. (Update: in some cases, dynamic programming and meet-in-the-middle solve the problem faster; see comments for details.)
Perhaps that is why I am doomed to carry my satchel until the end of my life, trying to speed up this program. I already rewrote the cycle in assembler once, having received a small increase in speed, and now I’m even thinking of making a multi-threaded version of the program. You can only sympathize with me. :)

KDPV: a satchel problem on a living example
Background
It all started 10 years ago when I was in ninth grade. I accidentally overheard the conversation of a computer science teacher telling a puzzle to one of the elders: a set of numbers was given, and another number was a control one. It is necessary to find the maximum sum of numbers from the set, which would not exceed the control number.
The task for some reason sunk into my soul. Having returned home, I quickly drew up a solution: a naive search of all possible amounts with the choice of the best. I got combinations by sorting through all N-bit binary numbers and taking the sums of those initial numbers to which the units correspond. But I regretfully found that with the number of elements starting somewhere around 30, the program runs for a very long time. It is not surprising, because the operating time of such an algorithm is n * 2 n (the number of combinations multiplied by the length of the sum).
5 years later. I managed to finish school and go to university, but this task was still with me. Once, leafing through the book "Algorithmic Tricks for Programmers" (Hacker's Delight / Henry S. Warren Jr.), I came across a description of the Gray code: this is a sequence of binary numbers, each of which differs from the previous one by only one bit. “Stop!” I thought. “That means ... Yes!” This means that in the same problem at each step of the search, you can not calculate the whole amount, but only add or subtract one number. " And I immediately went deep into the study of the topic.
Building Gray Code
Gray code can be constructed for a number of any bit depth. For one category, it is obvious:
0
1
To add a second category, you can add the same backward to this sequence
0
1
1
0
and add units to the second half:
00
01
11
10
Similarly for three categories:
000
001
011
010
110
111
101
100
Such a code, obtained by reflection of a code of lower bit capacity, is called a reflex (reflected) Gray code. There are other sequences, but in practice this is usually used.
This code is named after Frank Gray., which invented the tube ADC, which produced a digital signal in this code. With small changes in the input signal level, the digital output could change in only one bit, and this avoided sudden jumps due to non-simultaneous switching of bits.

Frank Gray Patent Illustration
The most obvious use of the Gray code is in angle sensors. A sensor similar to what was in old mechanical mice, but determining not the relative displacement, but the absolute value of the angle. For this, for each sensor, several optocouplers and several slotted gratings are needed. Moreover, each subsequent position of the sensor should differ from the previous one only in the state of one bit, otherwise at the borders non-synchronous switching of bits is possible, and, consequently, sharp jumps in the readings of the device. Here you can see a curious feature of the Gray code: the last number also differs from the first one by one bit, so it can be “looped”.

Sensor of absolute angle of rotation. Optical slots are arranged according to the Gray code.
Application in the Knapsack Problem
But back to the knapsack problem. The standard formula gives us the Gray code by number:
G = i ^ (i >> 1)
According to it, we can only calculate the sum of all the necessary elements. And we were going to add or subtract one value at each iteration, right? So, we need to get the numbers of the modified bits. For multi-digit numbers, these numbers will be like this:
0
1
0
2
0
1
0
3
0
1
0
2
0
1
0
4
...
Does it look like nothing? This is the bit number that we set to unity when we simply list ordinary binary numbers. Or else - the number of the minor unit in a binary number. This operation is called find first set.and on most processors it exists as a separate instruction. Visual C ++ provides this instruction as a _BitScanForward function.
So, now we are ready to write a program that solves the knapsack problem through the Gray code. We formulate the problem as follows:
In the input.txt file, the first line indicates the capacity of the backpack, and the remaining lines indicate the sizes of the things. In the console you need to display the maximum load of the backpack and the size of the selected things. Checking the correctness of input, etc. - see.
We will store a bitmask of used things, and add or remove one of them as necessary. To get by with ints, we limit the number of things (and bits used) to thirty-one.
#include
#include
#include
#include
using namespace std;
void main()
{
int target; // размер ранца
int nItems = 0; // количество предметов
int weight[31]; // веса предметов
ifstream inFile("input.txt");
inFile >> target;
while(inFile >> weight[nItems])
nItems++;
inFile.close();
const unsigned int nIterations = 1 << nItems; // количество комбинаций, 2^n
int sum = 0; // текущий вес вещей
int bestSum = 0; // лучший вес (максимальный без перегрузки)
bitset<31> mask; // текущая комбинация выбранных вещей
bitset<31> bestMask; // лучшая комбинация выбранных вещей
for (unsigned int i = 1; i < nIterations; i++)
{
unsigned long position; // какой по счёту бит инвертируем
_BitScanForward(&position, i);
mask[position] = !mask[position];
if (mask[position]) // кладём в рюкзак или убираем эту вещь
sum += weight[position];
else
sum -= weight[position];
if (sum > target) // перегруз
continue;
if (sum > bestSum) // Отличный вариант! Надо запомнить...
{
bestSum = sum;
bestMask = mask;
}
}
cout << "Best approximation: " << bestSum << endl;
cout << "Used weights:" << endl;
for (int i = 0; i < 31; i++)
if (bestMask[i])
cout << weight[i] << endl;
cin.get();
}
I apologize for the possible roughness; unfortunately, C ++ has long been not my core language.
It really works faster than assembling from scratch all the sums, the difference is already noticeable at 20 numbers, and at 30 I did not wait for the naive algorithm to complete, while the new version is completed in 7 seconds. However, given the exponential complexity, this is by no means small: for 50 numbers, using this algorithm no longer makes sense. Unfortunately, any exact algorithm will not work faster than in 2 n ; faster only an approximate solution is possible. (Update: in some cases, dynamic programming and meet-in-the-middle solve the problem faster; see comments for details.)
Perhaps that is why I am doomed to carry my satchel until the end of my life, trying to speed up this program. I already rewrote the cycle in assembler once, having received a small increase in speed, and now I’m even thinking of making a multi-threaded version of the program. You can only sympathize with me. :)
