A generic method for sorting complex information has been detected.
- Transfer

Opening your cafe, you would like to know the answer to the following question: “where is the other one closest to this point?” This information would help you better understand your competitors.
This is an example of the " nearest neighbor " search task , which is widely studied in computer science. Given a set of information and a new point, and you want to find which of the existing points it will be closest to? Such a question arises in many everyday situations in such areas as genome research, image search and recommendations on Spotify.
But, unlike the cafe example, questions about your nearest neighbor are often very difficult. Over the past few decades, the greatest minds among computer scientists have been looking for the best ways to solve such a problem. In particular, they tried to cope with the complications arising from the fact that in different data sets there can be very different definitions of the “proximity” of points to each other.
And now a team of computer scientists came up with a completely new way to solve the problem of finding the nearest neighbor. In a couple of papers, five scientists described in detail the first generalized method for solving the problem of finding the nearest neighbor for complex data.
“This is the first result covering a large set of spaces with the help of a unified algorithmic technique,” said Petr Indyk , an informatics specialist from the Massachusetts Institute of Technology, an influential figure in the field of development related to this task.
Distance difference
We are so tightly attached to the only way to determine the distance that it is easy to lose sight of the possibility of the existence of other ways. Usually we measure distance as Euclidean - as a straight line between two points. However, there are situations in which other definitions have more meaning. For example, the Manhattan distance makes you turn 90 degrees, as if moving along a rectangular network of roads. To measure a distance that in a straight line could be 5 kilometers, you may need to cross the city in one direction for 3 km, and then in the other - for 4.
It is also possible to talk about distances in a non-geographical sense. What is the distance between two people on the social network, or two films, or two genomes? In these examples, the distance indicates the degree of similarity.
There are dozens of distance metrics, each of which fits a specific task. Take, for example, two genomes. Biologists compare them using Levenshtein distance , or editing distance. The editing distance between two genome sequences is the number of additions, deletions, insertions and substitutions necessary to transform one of them into another.
Editing distance and Euclidean distance are two different notions of distance, and one cannot be reduced to one another. Such incompatibility exists for many pairs of distance metrics, and represents a barrier for computer scientists trying to develop algorithms for finding the nearest neighbor. This means that an algorithm that works for one type of distance will not work for another - more precisely, it has been so far until a new type of search has appeared.

Alexander Andoni
The square of the circle
The standard approach to finding the nearest neighbor is to divide the existing data into subgroups. If, for example, your data describes the location of cows in a pasture, then you can enclose each of them in a circle. Then we place a new cow on the meadow and ask the question: in which circle does it fall? It is almost guaranteed that the nearest neighbor of the new cow will be in the same circle.
Then repeat the process. Divide the circles into subcircles, divide these cells further, and so on. As a result, there is a cell with only two points: the existing one and the new one. This existing point will be your closest neighbor.
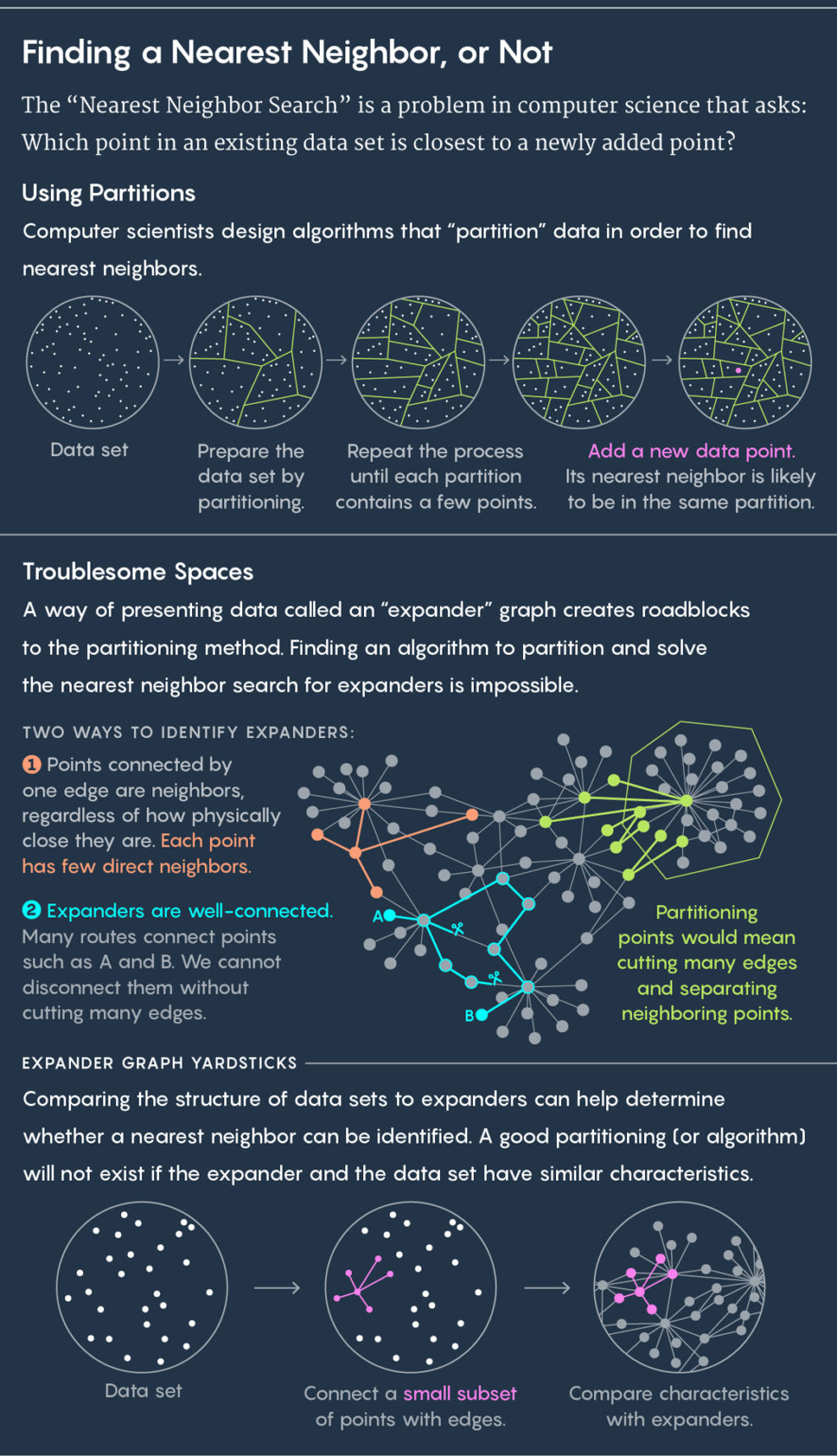
At the top - the division of data into cells. Below is the use of an expanding graph.
Algorithms draw cells, good algorithms draw them quickly and well — that is, in such a way that there is no situation in which a new cow falls into a circle and its nearest neighbor is in another circle. “We want the near points in these cells more often to be in the same disk with each other, and the distant ones rarely,” said Ilya Razenshtein , a computer science expert from Microsoft Research, co-author of the new work, in which Alexander Andoni from Columbia University also participated , Assaf Naor from Princeton, Alexander Nikolov from the University of Toronto and Eric Weingarten from Columbia University.
For many years, computer scientists have invented various algorithms for drawing such cells. For small-sized data - such, where one point is determined by a small number of values, for example, the location of a cow on a pasture - algorithms create so-called " Voronoi diagram ", just answer the question regarding the nearest neighbor.
For multidimensional data, in which a single point can be determined by hundreds or thousands of values, the Voronoi diagrams require too much computational power. Instead, programmers draw cells using " locally sensitive hashing, " first describedIndyk and Rajiv Motvani in 1998. LFC-algorithms draw cells in a random fashion. Therefore, they work faster, but less accurately - instead of finding the exact nearest neighbor, they ensure that a point is located no farther than a specified distance from the real nearest neighbor. This can be imagined as a recommendation from a movie from Netflix, which is not perfect, but good enough.
Since the late 1990s, computer scientists have come up with such LCH algorithms that provide approximate solutions for the task of finding the nearest neighbor for given distance metrics. The algorithms were very specialized, and the algorithm developed for one distance metric could not be used for another.
“You can come up with a very efficient algorithm for the Euclidean or Manhattan distance, for some specific cases. But we did not have an algorithm that would work on a large class of distances, ”said Indyk.
Since the algorithms that work with one metric could not be used for another, programmers came up with a workaround strategy. Through a process called “embedding” they imposed a metric, for which they did not have a good algorithm, on the metric for which it was. However, matching the metrics was usually inaccurate — something like a square peg in a round hole. In some cases, the embedding did not take place at all. It was necessary to come up with a universal way to answer the question about your nearest neighbor.

Ilya Razenstein
Unexpected result
In the new work, scientists abandoned the search for special algorithms. Instead, they asked a broader question: what prevents to develop an algorithm on a certain distance metric?
They decided that it was the unpleasant situation connected with the expanding graph, or the expander.. An expander is a special type of graph, a set of points connected by edges. Graphs have their own distance metric. The distance between two points of the graph is the minimum number of lines needed to go from one point to another. You can imagine a graph, which is a connection between people on a social network, and then the distance between people will be equal to the number of connections that divide them. If, for example, Julian Moore has a friend who has a friend who has Kevin Bacon in his friends, then the distance from Moore to Bacon is three.
An expander is a special type of graph, which has two, at first glance, contradictory properties. It has high connectivity, that is, two points cannot be separated without cutting several edges. At the same time, most of the points are connected with a very small number of others. Because of this, most of the points are far apart.
The unique combination of these properties - good connectivity and a small number of edges - leads to the fact that on expanders it is impossible to conduct a quick search for the nearest neighbor. Any attempts to divide it into cells will separate points that are close to each other.
“Any way of cutting an expander into two parts requires cutting multiple edges, which separates many closely spaced vertices,” said Weingarten, co-author of the work.
By the summer of 2016, Andoni, Nyokolov, Razenstein and Vaneygarten knew that it was impossible for the expanders to come up with a good algorithm to find the nearest neighbor. But they wanted to prove that such algorithms cannot be built for a variety of other distance metrics - metrics, when searching for good algorithms for which computer scientists are deadlocked.
To find proof of the impossibility of such algorithms, they needed to find a way to embed the expander metric into other distance metrics. By this method they could determine that other metrics have properties similar to the properties of expanders, which does not allow making good algorithms for them.

Eric Weingarten
Four computer scientists went to Assaf Naor, a mathematician at Princeton University, whose previous work was well suited to the topic of expanders. They asked him to help prove that expanders can be embedded in various types of metrics. Naor quickly returned with the answer - but not the one that they expected from him.
“We asked Assaf to help us with this statement, and he proved the opposite,” Andoni said.
Naor proved that expanders are not embedded in a large class of distance metrics, known as " normalized spaces"(which includes such metrics as Euclidean and Manhattan space). Relying on Naor's evidence, the scientists followed the following logical chain: if expanders are not embedded in the distance metric, then there should be a good way to break them into cells (because, as they proved the only obstacle to this are the properties of expanders) Therefore, there must be a good algorithm for finding the nearest neighbor -.. even if he has no one found
five researchers published their results in a paper , which they completed in November and released in April. This was followed by a second work that they have completed this year and publishedin August. In it, they used the information obtained when writing the first work to find a fast algorithm for finding the nearest neighbor for normalized spaces.
“The first work demonstrated the existence of a method of splitting a metric into two parts, but it did not contain a recipe for how to do this quickly,” said Weingarten. “In the second paper, we argue that there is a way to divide the points, and besides that this separation can be made using fast algorithms.”
As a result, for the first time new works generalize the search for the nearest neighbor in multidimensional data. Instead of developing specialized algorithms for certain metrics, programmers have a universal approach to search for algorithms.
“This is an ordered method for developing your nearest neighbor search algorithms at any of the distance metrics you need,” said Weingarten.
