The first part (code analysis) is here: https://habr.com/post/420725/ .

Algorithm

Description

The algorithm continuously performs the following steps:

1. Waiting until a new tetrimino is created.
2. Checks the type of the newly created Tetrimino, the type of the following Tetrimino (the figure in the preview field) and the contents of the playing field.
3. Explores all possible ways to add two tetrimino to the playing field and evaluates each probability.
4. Moves the newly created Tetrimino to match the location of the best detected probability.

Each of these steps is described in detail below.

Lock search

Consider a simplified version of Tetris, in which the figures do not fall automatically. The only way to bring the figure down is a soft descent. By removing the timings from the game, we can fully describe the state of the active Tetrimino by its position and orientation. The figure has a known place of initial creation, and the following operations are used to convert from one state to another:

• Move one step down
• Move one step left
• Move one step to the right
• Turn one counterclockwise
• Rotate one step clockwise

These operations are applicable only when the squares of the resulting tetrimino correspond to empty cells of the playing field. When it is impossible to move one step down, the state is considered to be blocked. However, since we have simplified Tetris and the blocking wait is essentially infinite, the locked state can be further transformed by other operations, performing slips and scrolling.

A set of blocked states with a minimum sequence of operations creating them can be found using a wide search (breadth-first search, BFS). As mentioned below, it uses a queue to store intermediate results.

1. Queued state when creating.
2. We deduce a status from queue.
3. We receive the subsequent states, applying operations of transformation.
4. If there is no downward movement among them, then the status removed from the queue is blocked.
5. We bring in the queue subsequent states that we have not yet visited.
6. If the queue is not empty, repeat from step 2.

The program presents each state as an object with the following fields:

{ x, y, rotation, visited, predecessor }

In preparation, the program creates a three-dimensional array of state objects (20 rows × 10 columns × 4 turns), initializing accordingly x, yand rotation.

The field visitedis marked when the status is enqueued. In BFS, this is permissible, because each subsequent state increases the total path length by 1. That is, by increasing the path length, it is impossible to create a subsequent state that needs to be inserted somewhere other than the end of the queue to maintain order.

The field predecessorindicates the state object from which the current state originates. It is set when the status is queued. The state of creation has no preceding states.

The set of blocked states detected during the search is determined by the type of tetrimino and filled blocks on the playing field. The sequence of the moves that generated them can be found out (in the reverse order), following the links predecessorto the creation state. When a constant PLAY_FASTis assigned a value at the beginning of a program true, it completely skips the preceding states, directly putting tetrimino on the field and blocking it.

A three-dimensional array of state objects, a queue, and a BFS are packed into a class. It has a search method that receives a playing field (two-dimensional array), a type of tetrimino and a listener. Each time a blocked state is detected, the playing field is updated by adding tetrimino to the appropriate place. Then, the modified playing field along with information about the changes is transmitted to the listener for processing. After the listener completes a return, the playing field is restored.

The listener is used to combine several search operations into a chain, which makes it possible to find all possible ways to add two (or more) tetrimino to the playing field. The first search engine in the chain performs BFS only once. However, the second search engine performs BFS every time the first search detects a blocked state. And so on, if there are other search engines in the chain.

The listener of the last search engine evaluates the changed playing field. When he finds the playing field better than what was previously investigated, he writes down the used object of the locked state, which at that time uses the first search engine in the chain. Since the first search engine performs BFS only once, the fieldspredecessorits state objects remain valid until the entire search process is completed. That is, the last listener essentially writes down the path that the first tetrimino should take in order to come to the best configuration of the playing field as a result.

Evaluation function

The estimated function assigns a value to a modified game field — a weighted sum of the various influencing parameters. The evaluation function used in this case is based on the function developed by Islam Al-Ashi . It uses the following parameters:

• Total number of cleaned rows : this is the total number of rows that will be cleared due to the addition of two tetriminos.
• Total height of the block : the height of the block is the height above the floor of the playing field on which the figure is blocked. This is the vertical distance to which a blocked figure would fall if you remove all other occupied squares of the playing field and preserve the orientation of the figure. The total blocking height is the sum of the blocking heights of two tetriminos.
• Total number of “well” cells : a cell-well is an empty cell located above all occupied cells in a column so that its left and right neighbors are occupied cells; when determining wells, the walls of the playing field are considered occupied cells. The idea is that the well is a structure that is open at the top, closed at the bottom and surrounded by walls on both sides. The likelihood of intermittent gaps in the walls of a well means that cell wells do not necessarily occur in a continuous heap within a column.
• The total number of holes in the columns : the hole in the column is an empty cell located directly below the occupied cell. The floor of the playing field is not compared with the cell above it. There are no holes in the empty columns.
• Total number of transitions in columns : a transition in columns is an empty cell adjacent to an occupied cell (or vice versa) within a single column. The combination of the topmost occupied column block with the empty space above it is not considered a transition. Similarly, the floor of the playing field is also not compared with the cell above it. Therefore, there is no transition in a completely empty column.
• Total number of transitions in the rows : the transition in the rows is an empty cell adjacent to the occupied cell (or vice versa) within the same row. Empty slots near the walls of the playing field are considered transitions. The total number is calculated for all lines of the playing field. However, completely empty lines are not counted in the total number of transitions.

El-Ashi suggested that the payload can be found using the algorithm "particle swarm optimization» (the particle swarm optimization, the PSO), which iteratively improves the collection of possible solutions imitation observed in nature swarm behavior. In our case, each solution is a vector of weights, and the fitness of a variant is determined by playing Tetris; this is the total amount of tetrimino during which he survived to the end of the game.

These ideas are applied in the Java version described below; it runs outside of FCEUX and can be configured for a non-graphical, memory-based game that runs at a much higher speed. After PSO preparation, I was surprised to see that the algorithm does not move further after the initial iteration. After this iteration, several randomly generated solutions have already played quite well. For several days, the size of this set decreased until there was only one option left. Here are the values ​​for this solution:

Parameter	Weight
Total number of cleaned rows	1.000000000000000
Total lock height	12.885008263218383
Total number of well cells	15.842707182438396
The total number of holes in the columns	26.894496507795950
Total number of transitions in columns	27.616914062397015
Total number of transitions in lines	30.185110719279040

The playing field was estimated by multiplying the parameters by the corresponding weights and adding the results. The lower the value, the better the solution. Since all parameters and weights have positive values, all parameters harm the overall assessment; each of them must be minimized. This also means that the best estimate is equal to 0.

Since these weights were chosen randomly, the range of suitable values ​​can be very wide. This particular set of numbers and the perceived relative importance of each parameter may not be significant. Nevertheless, it will be interesting to watch them carefully.

The least damaging parameter is the total number of rows cleared. The very fact that this parameter is harmful is counterintuitive. But the main goal of AI is survival. He does not aim for the most points. Instead, he plays conservatively, usually clearing the rows one by one. To get a Double, Triple or Tetris will have to grow a bunch, which goes against the long-term goal.

Next in the list is the total height of the lock. It can be minimized by dropping tetrimino as close to the floor as possible. This is a simple strategy that contributes to survival in the long run and, in the short run, to quality packaging of the pieces.

The weight assigned to the total number of well cells seems a little surprising, because experienced players usually deliberately build deep wells to collect several Tetris (combinations of four lines) in a row. But as mentioned above, this is a risky game, contrary to the main goal - survival. In addition, the number of wells is an indicator of "bumps" heap. A certain level of unevenness is beneficial when placing certain shapes or combinations of shapes. But high unevenness causes damage to the tight package.

The total number of holes in the columns is approximately half of the total number of transitions in the columns. These parameters can be combined and collapsed into a common related parameter, resulting in a more extensive and most harmful parameter: the total number of transitions.

The dense packing areas have a small number of transitions in all directions. Therefore, the basic strategy, which is driven by artificial intelligence, can be briefly described as follows: pack the figures as close as possible to each other.

Other options

Here is a list of a few more parameters that I experimented with during the development of AI:

• Heap height : occupied blocks can hang over empty cells, creating protrusions and holes; however, it is impossible to fix occupied blocks above completely empty lines. Therefore, the height of the heap is the number of rows that contain at least one occupied block.
• Total number of occupied columns : this is the number of columns that contain at least one occupied cell.
• Total number of occupied cells : the number of occupied cells on the playing field.
• Total Number of Connected Areas : Here the fill algorithm is used to count the number of continuously connected areas. In addition to finding busy "islands", he finds holes that stretch along both axes.
• Variance of column heights : this is a statistical measure of the magnitude of the scatter of column heights. It is an indicator of surface roughness.
• Total Adaption Value : Calculates the heap adaptation value for the next unknown figure. It counts the total number of ways in which 7 types of pieces can be added to the playing field without the appearance of new holes. For accurate counting, multiple BFS applications will be required. But for approximate counting the search tree can be very truncated.
• Average score of the next figure : this parameter deepens the search by analyzing all the possibilities for the next unknown figure. It uses other parameters for a separate arrangement of each type of figures, and then returns the average for 7 estimates. BFS is required for each placement of the shape.
• Average simulated game : the parameter simulates a series of games in Tetris, selecting figures using its own pseudo-random number generator and using AI to work with them. At the end of each game, the playing field is estimated using other parameters. Returns the average value for all batches.

All parameters can be customized by adding custom factors. For example, instead of simply counting the cleaned rows, you can assign your own weights for Single, Double, Triple and Tetris, by simulating a points system. If the simultaneous cleaning of several rows harms the long-term goal of survival, then a single weight can be assigned a negative weight, while others can get a positive one.

Another useful factor is the bias value. For example, a completely flat surface of a heap has a dispersion of heights of columns 0. But a perfectly flat surface does not adapt to S and Z, as well as other combinations of figures. Therefore, by subtracting a constant, the variance needs to be centered around optimal irregularities.

The adjusted and shifted parameters can be raised to some power so that they can be logarithmically or exponentially scaled before calculating the weighted sum. All these probabilities can be considered as additional weights that can potentially be optimized using methods like PSO.

Many of the parameters provide insight into how well the heap can handle additional pieces, such as those dealing with surface roughness, but “Total Adaptation”, “Average Assessment of the Next Figure” and “Average Simulated Game” evaluate the modified playing field insertion of figures not included in the two known. In the study of subsequent figures due to the rapid elimination of rows, the amount of additional knowledge obtained decreases with depth. This means that the past for a long time the party is not so important, and the course of the party in the distant future is also not very important. In fact, if the short sequence of pieces is randomly set incorrectly, the AI ​​quickly restores the course of the game, using the following few pieces to clear the affected rows.

Another aspect of parameter utility is computational overhead. Costs greatly increase because the evaluation function is called for each possible placement of two figures. Since the AI ​​must be able to play Tetris in real time, costly factors providing valuable information can be exchanged for more approximate techniques that run faster.

AI training

There are pathological sequences that can lead to Game Over, regardless of strategy. The simplest example is an infinite sequence of T and S S and Z, which, as shown in the animation, quickly causes the AI ​​to lose.


Since it takes days to run the AI ​​variant until several batches are completed and the average is calculated, it is completely impractical to use the average batch duration as the PSO control metric. Instead, it is possible to increase the difficulty of the game with controlled speed, increasing the frequency of S and Z, which in time will lead to the alternate creation of only this pair of figures.

I tried using this method of training, but found that teaching AI to work with frequent S and Z actually harms the ability to cope with evenly distributed random figures.

In an alternative method that was inspired by the B-Type game, the PSO metric control is the frequency of cleaning rows. The game field is a scheme of 10 lines of random garbage blocks, and each time a line is cleaned, a new line of garbage appears at the bottom, restoring the height of the heap. Since the playing field has a width of 10 columns, and each tetrimino consists of 4 squares, on average, the AI ​​should clear a row every 2.5 tetrimino. And to get rid of garbage, he must do it even faster.

Unfortunately, this technique also did not improve performance. One of the probable reasons is that random holes in the garbage do not exactly correspond to the lines that the AI ​​deals with in this gameplay. In addition, row cleaning is a short-term goal; greedy row cleaning will not necessarily improve long-term survival. From time to time, rows should not be touched to handle certain combinations of subsequent figures.

On his webpage Colin Faysuggested a different approach. He created a histogram showing the percentage of pieces blocked in each row during trial lots. Interestingly, all histograms look almost identical regardless of the number of created figures. Based on this, he suggested that it is possible to use an approximate image of a function for any trial game when evaluating the statistical wait for a block in a creation line, thus obtaining the time during which the AI ​​will play until the end of the game. I decided to explore this opportunity.

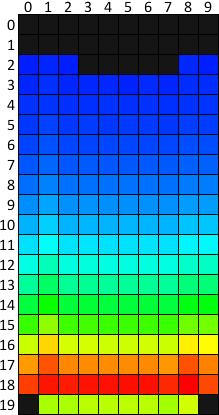
The following is a heat map of the set of test lots, totaling 2,039,900,000 tetrimino. Each cell is colored based on the percentage of figures blocked in it. To enhance the visual contrast is selected non-linear palette. The map was created by normalizing the cell values ​​by dividing by the maximum percentage of cells, and then by announcing to a degree of 0.19 (see “gamma correction” ).

Colour Percent ■ 0.00000000 ■ 0.00000315 ■ 0.00024227 ■ 0.00307038 ■ 0.01860818 ■ 0.07527774 ■ 0.23582574 ■ 0.61928352 ■ 1.42923040 ■ 2.98867416 ■ 5.78182519

The dark orange and red stripe in lines 17 and 18 means that the vast majority of the figures end up there. The pale green tint below is a consequence of the geometry of the figures: only 4 of the 7 types of tetrimino can appear on the bottom line. The bottom corners are black because it’s impossible to be there.

The color along each line is almost uniform, and this suggests that horizontally the figures are distributed evenly. Minor gaps can be explained by looking at the histograms of certain types of shapes:

T

J

Z

O

S

L

I

T turns out to be the most universal type: its histogram is more uniform than that of all others. Anomalies in the histogram J - the result of the influence of the walls; only Jrand Jlmay be in the side columns, which makes the AI to compensate for the increased use of columns 1 and 9. The same applies to L. Histograms Z and S look about the same, which underlines the imbalance due to the fact that Zv, and Svare not ideal mirror reflections of each other. Type O is limited to the 19 × 9 playing field, and the AI ​​seems to be more likely to use O on the sides than in the center. Tetrimino I is shifted to the right, because its starting point is located there; therefore, blocking in column 1 rarely happens.

The table shows the percentage of figures blocked in each row.

Line	Percent
0	0.0000000000
one	0.0000000000
2	0.0000004902
3	0.0000026472
four	0.0000066180
five	0.0000172557
6	0.0000512280
7	0.0001759400
eight	0.0006681210
9	0.0023187901
ten	0.0077928820
eleven	0.0259672043
12	0.0866187068
13	0.2901315751
14	0.9771663807
15	3.3000408353
sixteen	10.6989059268
17	28.5687976371
18	50.0335706162
nineteen	6.0077671454

Here is a graph of values:


If you do not take into account line 19, the graph shows exponential growth.

Below is a list of ratios of the number of locked figures in adjacent rows.

Line A / Line B	Ratio (%)
1/2	0.00
2/3	18.52
3/4	40.00
4/5	38.35
5/6	33.68
6/7	29.12
7/8	26.33
8/9	28.81
9/10	29.76
10/11	30.01
11/12	29.98
12/13	29.85
13/14	29.69
14/15	29.61
15/16	30.84
16/17	37.45
17/18	57.10
18/19	832.81

The lines 16–19take into account the figures that interact with the floor of the playing field, so they can be discarded. The rows are 0–5too sampled too small to be meaningful. The remaining ratios, pairs 6 / 7–14 / 15, are almost identical; their average value is 29.24%. This means that the probability that the heap will grow by one line is about the same, regardless of the height of the heap. This is quite logical, because the Tetris rules limit interactions at the top of the heap when it is packed tightly.

Below is a graph of log ₁₀ percent of the figures in lines 6–15.


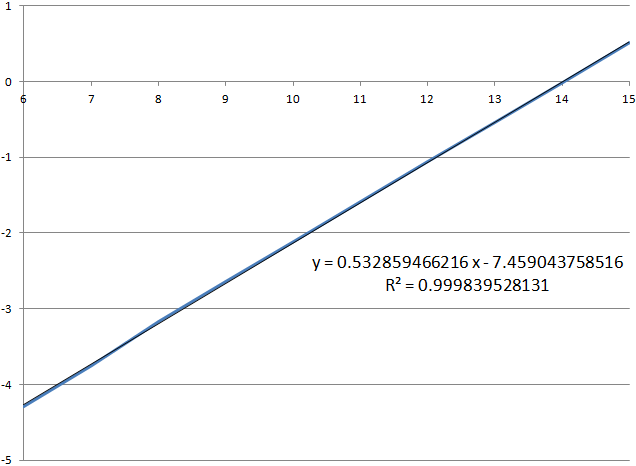
It is close to a perfectly straight line with a close to 1 coefficient of determination . The formula derived from the linear regression shown above gives us the intersection with the Y axis, suggesting that the percentage of the figures in line 0 is approximately 10 ^−7.459 %. The reciprocal of this value gives us a statistical expectation of 2,877,688,349 tetrimino, or 1,151,075,340 rows until the end of the game.

This makes us understand that log ₁₀The percentage of pieces in each line remains linear up to line 0. However, when the heap almost reaches the ceiling of the playing field, freedom of movement is limited to such an extent that this property is violated. In addition, blocking a shape in line 0 does not necessarily mean game over; you can still be saved if there is a place to create new shapes.

Another way to assess the strength of an AI is to measure the average number of pieces created between full cleansing of the playing field. Full cleaning can be obtained with just 5 tetrimino. For example, among other possibilities, this can be achieved with five O figures laid out on the floor of the playing field. In general, since each tetrimino consists of 4 squares and the playing field is 10 squares, the number of created figures between full cleansing should be a multiple of 5 ( because4 × 5n = 2 × 10n ).

My AI has an average number of created figures between full field cleansings of 1181, a rather small number. Because a full cleanup is similar to restarting a game, a full batch can be viewed as an extremely long series of restarts of a game, followed by a quick advance to game over. As with the alternating sequence described above S-Z, pathological sequences leading to the end of a game are usually very short.

The histogram below shows the probability (in percent) that the AI ​​will achieve a complete field clearance after the specified number of created figures.


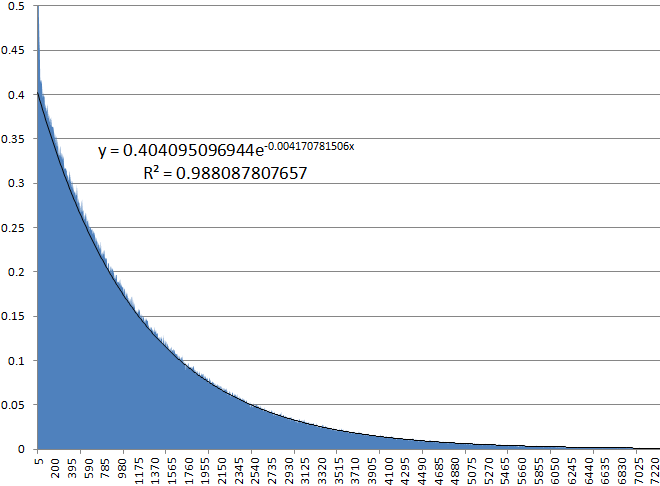
The order of degree in the formula shown above determines the rate of decrease and, presumably, the power of AI. According to this formula, approximately 0.4%, or about 1 of 253 games, starting from an empty playing field, are completed with a full cleaning in just 5 tetrimino.

Contrary to what Fay assumed, constants in linear and exponential approximations require a very large sample size so that R ²approached 1, so this method is not applicable for PSO. However, the constants obtained with long batches can be used to optimize the approximation function, which creates possible values ​​of the constants for short batches. In a kind of development feedback loop, an optimized approximation function can be used in the PSO, which improves the AI, which in turn can be used to calculate new constants, which serve as reference criteria for the approximation function.

Java version

About the program

For developers unfamiliar with Lua, I added a Java port to the source zip file . Classes are almost a line-by-line translation of Lua objects based on closures .

Packages

The code is divided into two packages:

• tetris.ai contains classes and interfaces of AI.
• tetris.gui creates a graphic model of the playing field.

AI Classes and Interfaces

The class with the appropriate name Tetriminosdescribes tetrimino. It is used like this enumand contains constants for all types of tetrimino:

publicstaticfinalint NONE = -1;
publicstaticfinalint T = 0;
publicstaticfinalint J = 1;
publicstaticfinalint Z = 2;
publicstaticfinalint O = 3;
publicstaticfinalint S = 4;
publicstaticfinalint L = 5;
publicstaticfinalint I = 6;

NONEmeans unassigned value. It is used for empty cells of the playing field.

It also Tetriminoscontains two models of the orientation table. PATTERNS- this is a 4-dimensional array integer (type × rotation × square × coordinates) containing relative coordinates of the squares; the rows are arranged in such a way that in each type the orientation of the shape creation is first. ORIENTATIONS- This is another model, a 2-dimensional array (type × turn) of objects Orientation. Each Orientationcontains the coordinates of a square as an array of objects Point. It also has fields that describe the range of allowed positions for the corresponding orientation.

publicclassOrientation{
  public Point[] squares = new Point[4];
  publicint minX;
  publicint maxX;
  publicint maxY;
  ...
}

publicclassPoint{
  publicint x;
  publicint y;
  ...
}

Tetrimino rotation (second index in both orientation tables) is used in objects Statemanipulated by BFS.

publicclassState{
  publicint x;
  publicint y;
  publicint rotation;
  publicint visited;
  public State predecessor; 
  public State next;
  ...
}

x, yand rotationtogether describe the position and orientation of the shape. Since the type of Tetrimino remains constant from the moment of creation to the lock, the field is optional for it.

The class Searcherthat contains the BFS algorithm creates, with a complete set of all possible objects Stateduring creation:

privatevoidcreateStates(){
  states = new State[AI.PLAYFIELD_HEIGHT][AI.PLAYFIELD_WIDTH][4];
  for(int y = 0; y < AI.PLAYFIELD_HEIGHT; y++) {
    for(int x = 0; x < AI.PLAYFIELD_WIDTH; x++) {        
      for(int rotation = 0; rotation < 4; rotation++) { 
        states[y][x][rotation] = new State(x, y, rotation);
      }
    }
  }
}

Although Java has a rich Collections API, it Searchercontains its own queue implementation. The class Queueuses State.nextto join objects Stateinto a linked list. Since all objects Stateare predefined, and each Statecan be added to the queue no more than once, the queue can work in place, which makes it possible to abandon unnecessary temporary container objects used in common queue implementations.

The “heart” of BFS is the method shown below search.

publicbooleansearch(int[][] playfield, int tetriminoType, int id){
  int maxRotation = Tetriminos.ORIENTATIONS[tetriminoType].length - 1;
  int mark = globalMark++;
  if (!addChild(playfield, tetriminoType, mark, null, 5, 0, 0)) {
    returnfalse;
  }    
  while(queue.isNotEmpty()) {
    State state = queue.dequeue();
    if (maxRotation != 0) {
      addChild(playfield, tetriminoType, mark, state, state.x, state.y, 
          state.rotation == 0 ? maxRotation : state.rotation - 1);
      if (maxRotation != 1) {
        addChild(playfield, tetriminoType, mark, state, state.x, state.y, 
            state.rotation == maxRotation ? 0 : state.rotation + 1);
      }
    }
    addChild(playfield, tetriminoType, mark, state, 
        state.x - 1, state.y, state.rotation);
    addChild(playfield, tetriminoType, mark, state, 
        state.x + 1, state.y, state.rotation);
    if (!addChild(playfield, tetriminoType, mark, state,
        state.x, state.y + 1, state.rotation)) {
      lockTetrimino(playfield, tetriminoType, id, state);
    }
  }
  returntrue;
}

It generates a queue with the state of the created tetrimino, and then successively extracts the child elements from the states quit, adding them back to the queue when they appear on the playing field.

The searchplaying field containing a combination of occupied and empty cells, the type of Tetrimino created and an arbitrary identifier are transferred to the method . During BFS execution, each time a lock position is detected, the listener is called.

publicinterfaceISearchListener{  
  publicvoidhandleResult(int[][] playfield, int tetriminoType, 
      int id, State state);
}

The listener receives a changed playing field containing a tetrimino blocked in place. Also the type of the created tetrimino and an arbitrary identifier are transferred. The last parameter is Statein which tetrimino is blocked. By following the link chain State.predecessor, you can restore all the way back to Statecreating a shape.

State.visitedcould be implemented as boolean; however, before searching, it would be necessary to iterate over all objects Stateto reset visitedto false. Instead, I made the visitedvalue intbeing compared with a counter, increasing with each call.

MethodaddChildpre-enqueues subsequent states. The subsequent state must be within the field and be located on 4 empty cells of the playing field. In addition, the subsequent state should be unvisited State. If the position is valid, addChildreturns trueeven if the subsequent state could not be queued because it was already visited.

The method searchuses the return addChildvalue to determine whether it is possible to create a shape. If the shape cannot be created, the heap has reached the top and the search can no longer be performed; so it returns false.

ReturnableaddChildthe value is also being studied for the possibility of going down another step. If this cannot be done, the current state is the blocking position and the call is started lockTetrimino. The method lockTetriminochanges the playing field, calls the listener, and then restores the playing field.

Each row of the array playfieldcontains 1 additional element, which stores the number of occupied cells in the row. The element increment is performed by the method lockTetriminobecause it marks the cells as occupied.

When the listener receives a modified playing field, he callsPlayfieldUtil.clearRowsto remove the filled rows; the method recognizes them, referring to the value in the additional element of the array. To remove a string, code takes advantage of the fact that in Java, two-dimensional arrays are essentially arrays of arrays; it simply shifts down the references to lines. PlayfieldUtilcontains free lines; it completes the cleaning process by inserting up a link to one of them. Before performing the shift, the index of the row being cleared is saved to the additional element of the row. Then the link to the string is written to the stack.

Then the listener callsPlayfieldUtil.restoreRowsto cancel changes made to the playing field. Steps are canceled in reverse order. First we get a free line from the vertex. Then the filled line is retrieved from the stack and the index is restored from the additional item. It is used to shift the links of lines and to return to the place of the deleted line. Finally, an additional element is restored, it is assigned the value of the playing field width - the number of occupied cells in the filled row.

There is PlayfieldUtilalso a method evaluatePlayfieldthat calculates and writes 4 evaluation parameters in the container class shown below.

publicclassPlayfieldEvaluation{
  publicint holes;
  publicint columnTransitions;
  publicint rowTransitions;
  publicint wells;
}

The class controls all of this AI. It contains two objects Searcherjoined together by the listener shown below.

publicvoidhandleResult(
    int[][] playfield, int tetriminoType, int id, State state){
  if (id == 0) {
    result0 = state;
  }
  Orientation orientation 
      = Tetriminos.ORIENTATIONS[tetriminoType][state.rotation];
  int rows = playfieldUtil.clearRows(playfield, state.y);
  int originalTotalRows = totalRows;
  int originalTotalDropHeight = totalDropHeight;
  totalRows += rows;
  totalDropHeight += orientation.maxY - state.y;
  int nextID = id + 1;
  if (nextID == tetriminoIndices.length) {
    playfieldUtil.evaluatePlayfield(playfield, e);
    double fitness = computeFitness();
    if (fitness < bestFitness) {
      bestFitness = fitness;
      bestResult = result0;
    }
  } else {
    searchers[nextID].search(playfield, tetriminoIndices[nextID], nextID);
  }
  totalDropHeight = originalTotalDropHeight;
  totalRows = originalTotalRows;
  playfieldUtil.restoreRows(playfield, rows);
}

A class AIcan process any number of objects Searcher, but Nintendo Tetris only shows one figure in advance. Objects Searcherare stored in an array, and the code shown above serves as their general listener. An arbitrary identifier passed to the method Searcher.searchis actually an array index, which is also the depth of the search. When calling a listener, the identifier forwards the call to the next Searcherin the thread. If he has reached the end of the array, he evaluates the playing field. And when he finds a playing field with a higher fitness rating, he records the blocked one Statefrom the first Searcherin the chain.

AIcontains a method searchthat receives the playing field and an array containing the types of the created and the next tetrimino. He returnsStatecontaining the position and rotation in which the first tetrimino should be blocked. He does not focus on the second tetrimino; on a subsequent call, he reevaluates the estimate. If the heap is too high and the chain Searcherfails to place both tetriminos, it AI.searchwill return null.

public State search(int[][] playfield, int[] tetriminoIndices){
  this.tetriminoIndices = tetriminoIndices;
  bestResult = null;
  bestFitness = Double.MAX_VALUE;
  searchers[0].search(playfield, tetriminoIndices[0], 0);
  return bestResult;
}

Call AI

Since the Java version is not tied to FCEUX, it can potentially be used for other projects. For those who are interested in integrating AI somewhere else, this section describes everything that is necessary.

First, create an instance AI, an instance, PlayfieldUtiland an array to store all known types of tetrimino. In addition, let's create a call-up PlayfieldUtil.createPlayfieldinstance of the playing field; it returns a two-dimensional array with an additional column, which we discussed above. You will probably also need a random number generator.

AI ai = new AI();
PlayfieldUtil playfieldUtil = new PlayfieldUtil();
int[] tetriminos = newint[AI.TETRIMINOS_SEARCHED];
int[][] playfield = playfieldUtil.createPlayfield();
Random random = new Random();

Initially, the playing field is empty, and all cells have a value Tetriminos.NONE. If you fill the cells programmatically, then do not forget to write in the playfield[rowIndex][AI.PLAYFIELD_WIDTH]number of occupied cells in each row.

Fill in the array of types of Tetrimino types of the initially created figure and the next figure, which in the usual case are manually selected.

tetriminos[0] = random.nextInt(7);
tetriminos[1] = random.nextInt(7);

Then we will transfer the game field and the array of types to the method AI.search. He will return State, in which you need to block the first tetrimino. If it returns null, then game over is inevitable.

State state = ai.search(playfield, tetriminos);

If you need a path from creating a shape to blocking, then pass to the Statemethod AI.buildStateList.

State[] states = ai.buildStatesList(state);

To update the playing field, we will pass it PlayfieldUtil.lockTetriminoalong with its type and object State. This method automatically clears the filled rows.

playfieldUtil.lockTetrimino(playfield, tetriminos[0], state);

Before re-calling, AI.searchyou must randomly select the next tetrimino.

tetriminos[0] = tetriminos[1];    
tetriminos[1] = random.nextInt(7);

All together it looks like this:

AI ai = new AI();
PlayfieldUtil playfieldUtil = new PlayfieldUtil();
int[] tetriminos = newint[AI.TETRIMINOS_SEARCHED];
int[][] playfield = playfieldUtil.createPlayfield();
Random random = new Random();
tetriminos[0] = random.nextInt(7);
tetriminos[1] = random.nextInt(7);
while(true) {
  // ... print playfield ...
  State state = ai.search(playfield, tetriminos);
  if (state == null) {
    break; // game over
  }
  playfieldUtil.lockTetrimino(playfield, tetriminos[0], state);
  tetriminos[0] = tetriminos[1];    
  tetriminos[1] = random.nextInt(7);
}

Instead of displaying the playing field in text form, you can use a more interesting way to display what is happening ...

Display of the playing field

The class TetrisFramesimulates the Nintendo Tetris graphics, including the behaviors described in the previous part of the article.


To see it in action, run tetris.gui.Main. As in the case of the Lua version, we can adjust the game speed by changing the value of the constant at the beginning of the file.

publicstaticfinalboolean PLAY_FAST = true;

TetrisFramehas 4 methods for manipulating the screen. The method displayTetriminorenders the active Tetrimino in the specified coordinates. It receives a delay parameter that causes the method to wait before returning the specified number of animation frames.

publicvoiddisplayTetrimino(int type, int rotation, int x, int y, int delay)

The method lockTetriminoblocks the figure in place. The rows counter, points, level and colors of tetrimino are updated accordingly, demonstrating expected curious behavior when the values ​​exceed the allowable values. Assigning a animatevalue to a parameter trueincludes animations for cleaning rows and screen flickering when receiving Tetris. The method is blocked until the animation is complete.

publicvoidlockTetrimino(int type, int rotation, int x, int y, boolean animate)

updateStatisticsAndNext performs the statistics counter increment for the newly created tetrimino and updates the display of the next figure.

publicvoidupdateStatisticsAndNext(int activeTetrimino, int nextTetrimino)

The method dropTetriminocreates a figure and allows it to descend under the influence of "gravity", without attempting to rotate or move it. Mainuses it for the last two figures when it AI.searchreturns null. If the parameter animatehas a value true, then if it is impossible to create a figure, the end of the game curtain will drop. As with all other methods, this method is blocked until the animation is complete. He returns trueonly when he can create a piece on a busy playing field.

publicbooleandropTetrimino(int type, boolean animate)

These 4 methods must be invoked by the worker thread, but TetrisFramemust itself be created in Event Dispatch Thread. To see how this is done, see class Main.

For fun, it Mainuses a class Randomizerthat simulates an offset pseudo-random number generator from Nintendo Tetris.

The package tetris.gui.imagescontains display-related files. tiles.png- this is a pattern table containing all tile graphics. background.datstores the identifiers of the tiles that make up the background; data extracted from $BF3F. A colors.datcontains bytes that generate unusual colors of squares, appearing from level 138.

ImageLoadercontains a table of NES palettes, and ImagePanea full set of displayed level values ​​is stored in it.

Other projects

Potentially, the code can be used instead of recording for demo mode. In fact, such a demo can be rendered forever, taking advantage of how quickly AI is able to clear the entire playing field. To achieve this, in the pseudo-random number generator we need to use some arbitrary constant as a seed, which will give us a deterministic sequence of tetrimino. The first two tetrimino sequences will be recorded. When the AI ​​reaches full field clearance, the next two tetriminos will be compared with the first two of the sequence. If they match (this event is expected after every 49 complete clearing of the field), then the same constant can be passed to the pseudo-random number generator, which will create an infinite demo loop. The cycle time can be very long to hide the fact that it is a cycle. Besides,

Another possibility of using AI is to create a "player against the computer." In multiplayer "Tetris", while clearing several lines at the same time, garbage lines appear in the lower part of the opponent's field, raising the playing field. The AI ​​must be able to protect itself from garbage for the same reason that it can play B-Type mode games. However, as said earlier, the AI ​​plays conservatively, usually seeking to clear one line at a time. That is, he will be able to defend himself from attacks, but is not able to attack. To be able to change his behavior, I created an interface called IChildFilter.

publicinterfaceIChildFilter{
  publicbooleanvalidate(int[][] playfield, int tetriminoType,
      int x, int y, int rotation);
}

AIhas an alternative constructor that gets an implementation IChildFilter. If present, IChildFilter.validateit serves as an additional check for the resolution of the child state; if it returns false, the child state is not enqueued.

WellFilter- this is the implementationIChildFilteraimed at picking up four rows (Tetris). Like live players, it gradually builds a well in the rightmost column of the playing field, line-up rising from the bottom up. Since it works line by line, it rejects child states, which add a square to the rightmost column. When the entire row, with the exception of the column-well, is full, the AI ​​goes to the next row. When 4 or more of these lines are ready, it allows the stick to fall into the well and get Tetris. In addition, the height of the heap is tracked; if it becomes too large, then it WellFilterceases to influence the AI.


To check it in work, make the Mainfollowing changes:

AI ai = new AI(new WellFilter());

WellFilterworks, but not very efficiently. It contains simple heuristics designed to demonstrate the concept. To get Tetris more often, you need to use a more sophisticated strategy, perhaps one that can be optimized using PSO.

In addition, you can use child state filtering to generate patterns. Below is an example of what is capable of PatternFilter.


PatternFilterbuilds images line by line upwards, similar to how it works WellFilter; however, instead of guarding the rightmost column, it PatternFilterapproves only child states that correspond to a particular pattern.

The constructor PatternFilterreceives the name of one of the images in the package tetris.gui.patternsthat it uses as a template. Each 20 × 10 image contains black and white pixels corresponding to the cells of the playing field.

AI ai = new AI(new PatternFilter("tetriminos"));

The line of code shown above creates the silhouettes of seven types of tetrimino.


One more example with a large T Trifimino angled.


One more example. If you look closely, you will see the name of the game.


As well as WellFilter, PatternFilteris nothing but proof of concept. The patterns he processes are limited to the bottom of the playing field due to the fact that attempts to obtain them usually end in a game over. However, this is an interesting idea that is worth further investigation.

Gamepad Version

The Lua script and the Java program ignore gravity; for them, the speed of descent is not important, because, depending on the configuration, they either teleport the figures immediately to the right place, or drag along any chosen path. In a sense, they simply mimic Tetris, not play it. However, there is another Lua script in the source zip file , which is played by generating signals from the gamepad buttons, which allows the game to control the movement of shapes, gravity and everything else.

Adding gravity greatly expands the search space, forcing the AI ​​to take into account tricky rules for manipulating shapes. Details of these rules are described in the first part of the article, and can be fully appreciated by direct study of the code. Here are the most important ones:

• Shapes are updated at levels in the following order: shift, turn, and descent.
• When clamping "Down" shift can not be performed.
• With the clamping "Left" or "Right" it is impossible to perform a soft descent.
• You can shift and rotate within one frame.
• You can perform a turn and a soft descent within one frame.
• It is possible to shift and automatically descend within one frame.
• You can perform rotation and automatic shift within one frame.
• You can shift, rotate and automatically descend within one frame.
• When you press A or B before you next press them you must release at least one frame.
• Pressing “Left” or “Right” causes the game to automatically shift every 6 frames after an initial delay of 16 frames. You can press and release "Left" or "Right" in each frame to make the pieces move faster.
• Holding down will trigger a soft descent in every second frame with an initial delay of 3 frames.
• The first shape created has a delay of 96 frames. A gentle descent cancels it, shifting and turning - no.

To adapt all these rules, it is necessary to embed historical information into the search states. They need fields in which the number of frames for holding each button and the number of frames after the last automatic descent will be stored. Each unique set of values, including coordinates x, yand the rotation of tetrimino characterize a separate and unique state. Unfortunately, the number of possibilities is so vast that a full search through this space is impractical. The AI ​​version for the gamepad examines only its subset.

AI uses an object Statewith the following fields:

{ x, y, rotation, Left, Right, Down, A, B, fallTimer, visited, predecessor }

Instead of using the automatic shift, the AI ​​in alternate frames presses and releases the shift button. Therefore, it only needs to monitor whether the button is pressed, and not how long it is pressed. Since no automatic rotation, the same idea applies to the buttons A and B. Therefore the field Left, Right, Aand Bcan be interpreted as listing containing one of the following values:

{ RELEASED, PRESSED }

On the other hand, for a soft descent, you need to initially hold down the "Down" button for three frames, which requires the existence of 4 states:

{ RELEASED, PRESSED_FOR_1_FRAME, PRESSED_FOR_2_FRAMES, PRESSED_FOR_3_FRAMES } 

Downincrementally increasing from value RELEASEDto PRESSED_FOR_3_FRAMES, at which a soft descent occurs. After that, it can get the value RELEASEDor return to PRESSED_FOR_2_FRAMES, causing a soft descent every second frame after the initial delay. It cannot be RELEASEDfrom PRESSED_FOR_1_FRAMEor from PRESSED_FOR_2_FRAMES.

In fact, the Lua code uses an integer constant, but the principle is the same.

Similarly, visitedand predecessor, fallTimerit is assigned the value obtained when writing in the subsidiary queue state; it fallTimerwill be one more than the value of the parent state. A state containing fallTimerequal to the speed of descent implies that automatic descent occurs in this frame, and in subsequent states of this state the valuefallTimerwill be equal to 0.

Each Searcherpre-defines an 8-мерныйarray containing all possible states ( 20 строк × 10 столбцов × 4 поворотов × 2 Влево × 2 Вправо × 4 Вниз × 2 A × 2 B), and BFS is executed similarly to the method shown for the трёхмерногоarray. The pseudocode shown below describes how subsequent states are derived from states queued up.

Slide = (Left == PRESSED) or (Right == PRESSED)
Rotate = (A == PRESSED) or (B == PRESSED)
if Down == RELEASED or Down == PRESSED_FOR_3_FRAMES then  
  if Down == RELEASED then
    nextDown = PRESSED_FOR_1_FRAME
  else
    nextDown = PRESSED_FOR_2_FRAMES
  end
  addChild(Down = nextDown)
  ifnot Rotate then
    addChild(A = PRESSED, Down = nextDown)
    addChild(B = PRESSED, Down = nextDown)
  end
  if Slide then
    addChild()
    ifnot Rotate then
      addChild(A = PRESSED)
      addChild(B = PRESSED)
    end
  else
    addChild(Left = PRESSED)
    addChild(Right = PRESSED)
    ifnot Rotate then
      addChild(Left = PRESSED, A = PRESSED)
      addChild(Left = PRESSED, B = PRESSED)
      addChild(Right = PRESSED, A = PRESSED)
      addChild(Right = PRESSED, B = PRESSED)
    end
  end
elseif Down == PRESSED_FOR_1_FRAME then
    nextDown = PRESSED_FOR_2_FRAMES
  else
    nextDown = PRESSED_FOR_3_FRAMES
  end
  addChild(Down = nextDown)
  ifnot Rotate then
    addChild(A = PRESSED, Down = nextDown)
    addChild(B = PRESSED, Down = nextDown)
  end  
end

As shown in the pseudocode described below, the function addChildtakes into account the order of events occurring in each frame (for example, shift, rotation, and descent).

nextFallTimer = fallTimer + 1if Left == PRESSED and testPosition(x - 1, y, rotation) then
  x = x - 1
elseif Right == PRESSED and testPosition(x + 1, y, rotation) then
  x = x + 1 
end
if A == PRESSED and testPosition(x, y, nextClockwiseRotation) then
  rotation = nextClockwiseRotation
elseif B == PRESSED and testPosition(x, y, nextCounterclockwiseRotation) then
  rotation = nextCounterclockwiseRotation    
end
if Down == PRESSED_FOR_3_FRAMES or nextFallTimer >= dropSpeed then
  if testPosition(x, y + 1, rotation) then
    y = y + 1
    nextFallTimer = 0else
    lockTetrimino()
    return
  end
end       
childState = states[y][x][rotation][Left][Right][Down][A][B]
ifnot childState.visited then
  childState.visited = mark
  childState.predecessor = state  
  childState.fallTimer = nextFallTimer  
  queue.enqueue(childState)
end

As in the previous version, AI.searchreturns a chain of objects State. But in this case, each Statecontains a lot of buttons that need to be pressed in each frame. Fields x, yand are rotationnot used to manipulate shapes, but they can be used to verify the correctness of movement of shapes.

Although the search space is significantly reduced due to the limitations described above, it still takes 1–3 seconds to complete the search. If you run it, you will notice a pause after creating each tetrimino. In addition, the movements look very unnatural; usually a turn is made a moment before blocking. However, this AI plays almost the same as the version that ignored gravity, even at maximum speed.

To test it, runlua/NintendoTetrisAIGamepadVersion.luain the source zip file .

A simpler way to account for gravity is to limit the movement of the figures only by turning, followed by a shift, and then descending to the bottom. The idea is that if you get rid of slipping and scrolling, then the vertical speed of movement of the figures will have little effect on AI; all he needs to do is deliver the figure to the correct column, and gravity will do the rest. Another advantage of this technique is that the search space is very small, which allows you to play in real time, without delay for calculations. However, the disadvantage of this approach is that, without slipping and scrolling, the AI ​​plays much worse. However, Tetris AI, unable to play in real time, is almost useless.

Addition

Earlier, I wrote a plugin that procedurally imitated a player in Tetris. However, my project had some flaws:

1. The bot turned off gravity, allowing you to perform slips and scrolls that exceed the player’s ability at the lowest possible level of Nintendo Tetris. He never raises a piece down, but the only way to pull a piece down is controlled soft descent. That is, he plays in a theoretical, idealized world. If it is rougher, then he cheats.
2. Bot avoids risk. His main goal is long-term survival, not a set of maximum points. He fears bringing double, triple and Tetris glasses because they are associated with an increase in the heap of figures - an unnecessary risk that increases the likelihood of field overflow. Therefore, the maximum number of points is not reached to level 90. But in a real game where gravity exists, most players cannot beat level 29 or higher due to the extremely high speed of the descent of the figures.
3. Analytical abilities of a bot are based on a weighted sum of various influencing factors. But the weights were chosen randomly. He plays well only by coincidence. This is another evidence that Tetris is almost without difficulty without gravity.

In this section, I will talk about an improved bot playing Nintendo Tetris without turning off gravity. He assesses the risk and manages it, aggressively seeking to gain the maximum amount of points before reaching a high speed of descent.

---

Video

Observe how the bot scores the maximum number of Nintendo Tetris points, starting at level 19 in all the videos shown below.

---

Download

TetrisAI_2018-01-28.zip

The file .zipcontains:

• src - source tree.
• TetrisAI.jar - compiled binary file.
• lgpl-2.1.txt - free software license.

---

Launch

Prerequisites

• Nintaco - NES / Famicom emulator.
• Tetris (U) [!].nes - Nintendo Tetris ROM file.

Running plugin

1. Launch Nintaco and open Tetris (U) [!].nes.
2. Extract TetrisAI.jarfrom downloaded .zip.
3. Open the Run Program window by selecting Tools | Run Program ...
4. Enter the file path in the JAR name field or navigate to the file using the Find JAR ... button.
5. Click Load JAR to load it.
6. Click Run.
7. The plugin will automatically skip the legal information and splash screens, taking you directly to the menu screen GAME TYPEand MUSIC TYPE. Use D-pad(keyboard arrows in the default layout) A-TYPEand select any music. Then press Start (Enter) to go to the next menu screen.
8. On the menu screen, A-TYPEuse the D-pad(arrow keys) and select LEVEL 9. Finally, hold down the gamepad button Aand press Start (hold the keyboard key Xand press Enter) to start at level 19, and transfer control to the bot.

It is worth considering that the bot is designed only for level 19 and above. At lower levels he will not be able to control the figures.

Speed ​​reference

To make the game go faster, select Machine | Speed ​​| Max.

---

Details

Plateau

Below level 10, the speed of descent at each level is slightly higher than the previous one. But at level 10 and above there are several plateaus where speed remains constant for several levels. This is a consequence of the way the trigger mechanism works. The speed is represented as the number of frames per descent, which is an integer value. That is, for higher levels, there are not so many options: 10–12, 13–15, 16–18, 19–28, and 29+ are 5, 4, 3, 2, and 1 frame per descent.

The bot was designed taking into account only the 19-28 plateau. In the even frames, he clicks on the gamepad "Left", "Right", A, B or nothing. And in odd frames, it allows automatic descent without pressing any buttons. It seems that the game does not perceive horizontal movement, which coincides with the turn; therefore, each button is pressed independently in even frames.

Unlike masters who play at high levels, the bot does not take advantage of the delayed auto-shift (DAS), also known as “auto-repeat”, and related techniques. His work is more reminiscent of Thor Akerlund's vibrating thumb technique . However, it increases the frequency of vibration to the theoretical maximum allowed by the game.

Players are rewarded with 40, 100, 300 and 1200 points for Single, Double, Triple and Tetris. And the points are multiplied by the level number plus 1. In other words, to get the maximum score, the player must strive for the maximum amount of Tetris, playing at high levels as long as possible.

Level 19 is the highest, which can be chosen as the initial one, which allows the bot to jump immediately to the plateau 19-28. However, due to a bug in the level calculation mechanism that I mentioned in the previous part, the game will go to level 20 after clearing 140 rows, instead of 200 expected. After that, the game will change levels every 10 rows. However, after reaching 230 rows, the bot will rise from the plateau and quickly surrender. That is, he needs to get as many Tetris as possible before cleaning the 230 rows.

Soft descent

Soft descent can also increase the number of points. To get points, the figure must be gently lowered down to the lock on the playing field. Any short-term soft descent that occurs along the way when positioning the figure will not affect the score. If the player descends successfully, the player will receive one point for each line crossed during a soft descent. And the resulting value is not multiplied by the level number, even if a soft descent results in the cleaning of rows.

A gentle descent has little effect on the overall score. However, if possible, the bot completes the placement of the figure by pressing "Down" to get these points. In rare cases, he can average the difference between a very high score and exceeding the maximum value of points.

AI algorithm

When creating a shape, the bot explores every possible placement of the current and next shapes. Acceptable placement is the position in which the figure rests either on occupied cells or on the floor of the playing field. From the place where the shape is created, this position can be reached through a sequence of horizontal movements, turns and descents. Acceptable placements and paths to them are found using BSF.

Placing a piece on the playing field has consequences: 4 empty cells become occupied, and all filled rows are cleared, moving the lines down. For each valid placement of the current shape and its associated effects, the bot checks each valid placement of the next shape, evaluating the combination of consequences. Such a chain of searches is presented SearchChain.

Each of the combined effects is passed to the evaluation function, which calculates the contents of the playing field. The combination with the lowest score wins and the current figure is placed accordingly. Search chain results only affect the current shape. When creating the next figure, it is evaluated in combination with the next figure, and so on.

Evaluation function

The evaluation function is the weighted sum of the following parameters:

• The total number of cleaned rows is the number of rows cleaned by the addition of both tetrimino.
• The total blocking height is the sum of the heights above the playing field floor where tetrimino is blocked. The height of the blocking of a single piece is the vertical distance to which it can fall while maintaining orientation if all occupied squares of the playing field are removed.
• The total number of well cells is the number of cells inside the wells.
• The total number of deep wells is the number of wells containing three or more well cells.
• The total number of holes in the columns is the number of empty cells, directly above which there are occupied cells. The floor of the playing field is not compared with the cell above it. Empty columns do not contain holes.
• The total weighted number of holes in the columns is the sum of the row indices of the holes in the columns. In this case, the lines are indexed from top to bottom, starting from 1. The idea is that the holes located below in the heap give a greater penalty, because fewer lines are needed to fill the upper holes.
• The total number of hole depths in the columns is the sum of the vertical distances between each hole and the top of the column in which it is located. A vertex is the topmost occupied cell within a column, and a hole depth is the difference between the index of the hole row and the index of the vertex row.
• The minimum depth of the holes in the columns is the minimum depth of the holes in the columns. If there are no holes, then by default the parameter has the field height value (20).
• The maximum depth of the holes in the columns is the greatest depth of the holes in the columns. If there are no holes, then the default value is 0.
• The total number of transitions in the columns is the number of empty cells adjacent to the occupied cell (or vice versa) within one column.
• Total number of transitions in the rows : the transition in the rows is an empty cell adjacent to the occupied cell (or vice versa) within the same row. Empty slots near the walls of the playing field are considered transitions. The total number is calculated for all lines of the playing field. However, completely empty lines are not counted in the total number of transitions.
• The total number of column heights is the sum of the vertical distances between the top of each column and the floor of the board. A column containing only 1 occupied cell has a height of 1, and a completely empty column has a height of 0.
• The height of the heap is the height of the largest column.
• The scatter of column heights is the height difference between the highest and lowest columns.
• The total number of occupied cells - the number of occupied cells on the playing field.
• The total weighted number of occupied cells is the sum of the heights of all occupied cells. The line above the floor has a height.
• The dispersion of column heights is the sum of the absolute differences between the heights of all adjacent columns.

Machine learning

To find the weights of the evaluation function, we used the variant of the particle swarm optimization method (Particle Swarm Optimization, PSO), described in the footnote [1]. To obtain good convergent behavior, the proposed inertia and acceleration coefficients are applied. And the maximum sizes of the particle steps are determined by the limitation of their velocity values.

During each iteration, the particles were evaluated in parallel in order to fully utilize the available computing resources. In addition, after detecting convergence (no improvement after a certain number of iterations), the PSO tuned to an automatic restart with randomly selected weights, which allowed even more exploration of the search space.

Each particle position vector was estimated by simulating the execution of 100 batches on a plateau of levels 19–28. A full batch means clearing 230 rows, but many ended with a field overflow. Batch estimates were sorted, and the particle estimate was determined as the average for 33 out of 100 batches. The idea was to choose on the basis of aggressiveness. Particles in the upper third get used only to the desired sequences of figures, which limits the need for a conservative game. As a result, they tend to push the usual game to the brink, waiting for the next “stick”.

The pattern sequences for 100 batches were generated prior to the PSO, and the same sequences were used over and over. It was necessary to fix the search space so that the solutions could be compared with each other. The sequences were created using the logic of the present PRNG Nintendo Tetris, which is designed to reduce the chances of duplicates following each other. But PRNG also has weak points (see the section “Choosing Tetrimino” from the previous article): it doesn’t pick shapes evenly.

Initial attempts gave bots acting too aggressively. If they overcame a plateau of 19–28, they usually reached the maximum score. But, unfortunately, they often led to an overflow of the field too early. In response to this, four steps were taken to “calm” the bots:

1. They were ordered to be greedy: if the current or next figure can give Tetris, then make it. Before this directive, bots used “sticks” to further grow an ideally clean pile with a very deep well. Greedy behavior can potentially replace long-term survival with short-term benefits. But bots don't have to survive endlessly; it is enough for them to reach 230 rows. Experiments have shown that obtaining Tetris combinations with the possibility of facilitating this task. However, the same cannot be said about Single, Double or Triple. Greedy desire for them led to the creation of too conservative bots; they reached the end of the plateau with too low a score.
2. They were ordered not to put blocks close to the ceiling of the playing field. A penalty applied to the cells occupied in any of the top 7 rows was added to the evaluation function. The penalty is inversely proportional to the vertical distance between the unit and the ceiling.
3. The bots are ordered that when they are forced to place a block near the ceiling of the field, they should at least do it not at the point of the figure creation. In the current state, the search chain rejects placement combinations that may prevent the creation of any of the 7 tetrimino.
4. When placing the block supporting the ceiling, they were ordered to do so that it did not divide the playing field, which would make further development impossible. If the search chain detects contact with the ceiling, it fills from the point of creation of the shapes. And if the fill cannot completely fill the entire row, then the search string rejects the placement combination.

After applying all these rules to “calm” bots, the PSO method gave the following weights:

Parameter	Weight
Total number of cleaned rows	0.286127095297893900
Total lock height	1.701233676909959200
Total number of well cells	0.711304230768307700
Total number of deep wells	0.910665415998680400
The total number of holes in the columns	1.879338064244357000
Total weighted number of holes in columns	2.168463848297177000
The total number of hole depths in the columns	−0.265587111961757270
Minimum hole depth in columns	0.289886584949610500
Maximum hole depth in columns	0.362361055261181730
Total number of transitions in columns	−0.028668795795469625
Total number of transitions in lines	0.874179981113233100
Total number of column heights	−0.507409683144361900
Heap height	−2.148676202831281000
Scatter column heights	−1.187558540281141700
Total number of occupied cells	−2.645656132241128000
Weighted total number of occupied cells	0.242043416268706620
Dispersion of column heights	0.287838126164431440

Since the chain tends to a combination that minimizes the evaluation function, parameters with positive weights can be considered bonuses, and the rest - fines. But the weights do not necessarily show the significance of the corresponding parameters; they are not normalized, so they cannot be compared.

AI power

To assess the strength of AI, approximately 1.7 million results (with glasses) of simulated games were collected on a 19-28 plateau. The score does not reflect the game at level 29 or higher, and does not take into account points obtained from a soft descent. However, it includes the game, prematurely completed due to overflow fields. The Nintendo Tetris PRNG logic was used to generate tetrimino sequences.

Among these results, the largest score is 1,313,600. The minimum is 0. The

average value is 816,379, and it seems that it is not enough. But as mentioned below, the data is distorted, so the median score gives a better idea of ​​the typical value - 989,200 points.

As stated above, PSO has optimized weights based on the average of the best third of batches. In this case, the average score of the best third is 1,108,860. In fact, the average score of the best 75% is 1,000,000. The

bot has a 47% chance of reaching the limit of points to level 29. It has a probability of 61% receiving 900,000 points to 29. The graph below shows the probabilities of scoring points to level 29.


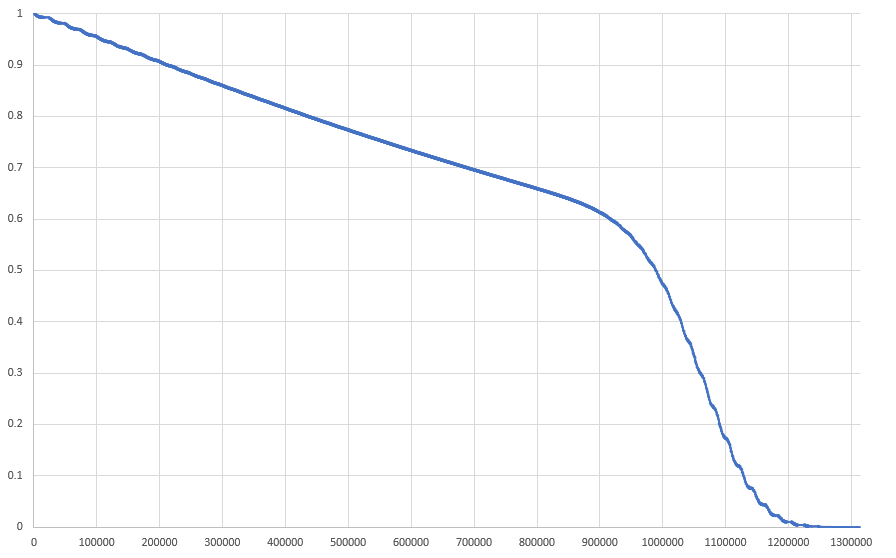
It seems that the probability of linearly reduced to about 900,000 points. Then it goes into an inverted sigmoid curve.

Below is a smoothed histogram with the number of batches for each of the accumulated points. Its shape is determined by the derivative of the graph shown above.


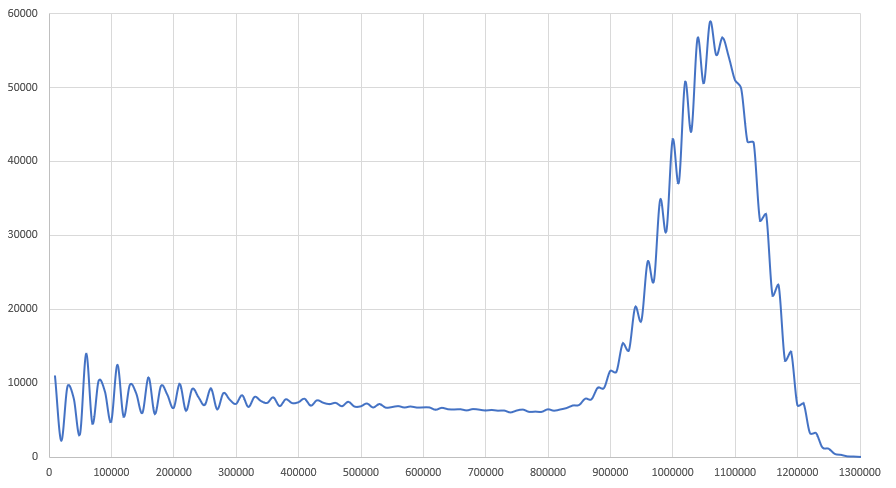
If you ignore the fluctuations, then to about 900,000 it is flat, and then goes into a normal distribution with a center around about 1,050,000 points. The reasons for the fluctuations are not clear. It seems that the number of points prefers to jump in increments of 20,000 points. Perhaps this is due to the cycle of building a heap and getting Tetris.

RAM and ROM distribution

The plugin uses the Nintaco API to manipulate CPU memory, transmit button presses, and receive frame-rendering events . All memory addresses are detected using the Nintaco debugging tools, and information is added to the Data Crystal ROMhacking.net wiki . In the source code, they look like constants in the interface Addresses.

---

Reference materials

1. van den Bergh, F .; Engelbrecht, AP (2006)
   A study of particle swarm optimization trajectories
   In: Information Sciences 176 (2006) (pp. 937–971)
   Retrieved from http://researchspace.csir.co.za/dspace/bitstream/handle/10204 /1155/van%20den%20bergh_2006_D.pdf