Reed-Solomon codes. Simple example
Thanks to the Reed-Solomon codes, you can read a CD with a lot of scratches, or transmit information in conditions of communication with a lot of interference. On average, for a CD, code redundancy (i.e. the number of additional characters that can be used to recover information) is approximately 25%. In this case, you can restore the amount of data equal to half the redundant. If the disk capacity is 700 MB, then, it turns out, theoretically it is possible to restore up to 87.5 MB from 700. At the same time, we do not need to know which symbol was transmitted with an error. It is also worth noting that interleaving is used together with coding, when the bytes of different blocks are mixed in a certain order, which as a result allows you to read disks with extensive damage localized close to each other (for example, deep scratches), since after the operation,Let's take a simple example and try to go all the way - from coding to receiving the source data at the receiver. Suppose we need to pass a codeword C consisting of two numbers - 3 and 1 in exactly this sequence, i.e. we need to transfer the vector C = (3,1). Suppose we want to fix a maximum of two errors, not knowing exactly where they might appear. To do this, take 2 * 2 = 4 redundant characters. We write them with zeros in our word, i.e. C is now (3,1,0,0,0,0). Next, you need to understand a little about mathematical features.
Fields Galois
Many people know the romantic story of a young man who lived only 20 years and one night wrote his mathematical theory, and was killed in a duel in the morning. This is Evarist Galois . He also tried several times to enter universities, but the examiners did not understand his decisions, and he failed the exams. He had to learn on his own. Neither Gauss nor Poisson, to whom he sent his works, also understood them, but his theory was very useful in the 60s of the twentieth century, and is actively used in our time both for theoretical calculations in new branches of mathematics, and practice.
We will use rather simple conclusions following from his group theory. The main idea - there is a finite (not infinite) number of numbers, called a field, with which you can carry out all known mathematical operations. The number of numbers in the field must be a prime number to any natural degree, however, in the case of the simple Reed-Solomon codes discussed here, the dimension of the field is a prime number in degree 1. In extended Reed-Solomon codes, the degree is greater than 1.
For example, for a Galois field of dimension 7, i.e. GF (7), all mathematical operations will occur with numbers 0,1,2,3,4,5,6.
Example addition: 1 + 2 = 3; 4 + 5 = 9 mod 7 = 2. Addition in Galois fields is modulo addition. Subtraction and multiplication are also done modulo.
Example of division: 5/6 = 30/36 = 30 / (36 mod 7) = 30/1 = 30 = 30 mod 7 = 2.
The construction of a degree is similar to multiplication.
A useful property is found in Galois fields when exponentiation. As you can see, if you raise to the power 3 or 5 in the selected Galois field GF (7), the line contains all the elements of the current Galois field except 0. Such numbers are called primitive elements. Reed-Solomon codes usually use the largest primitive element of the selected Galois field. For GF (7) it is equal to 5.
It can be noted that the numbers in the Galois fields are, at the same time, abstractions that have a closer relationship with each other than the numbers we are used to.
Interpolation
As many have known since school, interpolation is the finding of a polynomial of minimal degree in a given set of points. For example, there are three points and three values of some function at these points. You can find a function that satisfies this input. For example, this is very simple to do using the Lagrange transform. After the function is found, you can build a few more points, and these points will be associated with the three starting points. Generating redundant characters during encoding is an operation similar to interpolation.
Inverse Discrete Fourier Transform (IDFT)
The Fourier transform , along with the theory of Galois groups, is another pinnacle of mathematical thought, which is used today in many areas. Some even believe that the Fourier transform describes one of the fundamental laws of the universe. The main point: any non-periodic signal of finite length can be represented as the sum of sinusoids of different frequencies and phases, then you can reconstruct the original signal from them. However, this is not the only description. The numbers in the Galois fields resemble the mentioned different frequencies of the sinusoids, so the Fourier transform can also be used for them.
The discrete Fourier transform is the Fourier transform formula for discrete values. The conversion has two directions - direct and reverse. The inverse transform is mathematically simpler, so let's code the word under consideration C = (3,1,0,0,0,0) with it. The first two characters are information, the last four are redundant and always equal 0.
We write the code word C in the form of a polynomial: C = 3 * x 0 + 1 * x 1 + 0 * x 2 + ... = 3 + x. As a Galois field, we take the aforementioned GF (7), where the primitive element = 5. By doing the IDFT, we find the values of the polynomial C for the primitive element z of different degrees. IDFT formula: c j = C (z j ). That is, we find the values of the function C (z j), where j are the elements of the Galois field GF (7). We count to j = N-2 = 7-2 = 5 degrees. Looking at the degree table, one can guess why: to the sixth degree, the value is again 1, i.e. repeats, as a result of which it would then be impossible to determine to what extent they were raised - in the 6th or 0th.
s 0 = C (z 0 ) = 3 + 1 * z 0 = 3 + 1 * 5 0 = 4
s 1 = C (z 1 ) = 3 + 1 * z 1 = 8 = 1
s 2 = C (z 2 ) = 3 + 1 * z 2 = 0
...
Thus, C (3,1,0,0,0,0,0) => s (4,1,0,2,5,6).
We pass the word c (4,1,0,2,5,6).
Error
An error is another word that sums up with the transmitted. For example, the error f = (0,0,0,2,0,6). If done with + f, then we get with f (4,1,0,4,5,5).
Direct Fourier Transform (DFT). Decoding. Syndrome
At the receiver, we got the word c + f = c f (4,1,0,4,5,5). How to check if there were transmission errors? It is known that we encoded information using IDFT in GF (7). DFT (Discrete Fourier Transform) is the inverse of the IDFT. Having done it, you can get the initial information and four zeros (i.e., C (3,1,0,0,0,0)), in case there were no errors. If there were errors, then instead of these four zeros there will be other digits. Let's do the DFT for with f and check if there are any errors. DFT formula: C k = N -1 * c (z -kj ). The primitive element z = 5 of the field GF (7) is still used.
C 0 = c (5 -0 * j ) / 6 = (4 * 5 -0 * 0 + 1 * 5 -1 * 0+ 0 * 5 -2 * 0 + 4 * 5 -3 * 0 + 5 * 5 -4 * 0 + 5 * 5 -5 * 0 ) / 6 = (4 + 1 + 4 + 0 + 5 + 5) / 6 = 19/6 = 5/6 = 30/36 = 30 = 2;
C 1 = c (5 -1 * j ) / 6 = (4 * 5 -0 * 1 + 1 * 5 -1 * 1 + 0 * 5 -2 * 1 + 4 * 5 -3 * 1 + 5 * 5 -4 * 1 + 5 * 5 -5 * 1 ) / 6 = (4 + 3/15 + 24/750 + 20/2500 + 25/15625) / 6 = (4 + 3 + 24 + 20 + 25) / 6 = 76/6 = 456/36 = 456 = 1;
C 2 = c (5 -2 * j ) / 6 = (4 * 5 -0 * 2 + 1 * 5 -1 * 2 + 0 * 5 -2 * 2 + 4 * 5 -3 * 2 + 5 * 5-4 * 2 + 5 * 5 -5 * 2 ) / 6 = (4 + 2 + 4 + 10 + 20) / 6 = 40/6 = 240/36 = 240 = 2;
...
with f (4,1,0,4,5,5) => C f (2,1, 2,1,0,5 ). The highlighted characters would be zeros if there were no error. Now you can see that the error was. In this case, the symbols 2,1,0,5 are called the error syndrome.
Berlekamp-Messi Algorithm for Calculating Error Position
To fix the error, you need to know which characters were transmitted with the error. At this stage, it is calculated where the erroneous characters are, how many errors were, and also whether it is possible to fix such a number of errors.
The Berlekamp-Messi algorithm is looking for a polynomial that, when multiplied by a special matrix prepared from the numbers of the syndrome (example below), will return a zero vector. The proof of the algorithm shows that the roots of this polynomial contain information about the position of characters with errors in the resulting codeword.
Since the maximum number of errors for the case under consideration can be 2, we write the formula of the desired polynomial in the matrix form for two errors (polynomial of degree 2): Г = [1 Г1 Г2].
Now we write the syndrome (2,1,0,5) in the Toeplitz matrix format. If you look at the syndrome and the resulting matrix, you will immediately notice the principle of creating such a matrix. The dimension of the matrix is due to the polynomial Γ indicated above.
Equation to solve:
Elements under question marks do not affect the result. It is necessary to find G1 and G2, they are responsible for the position of errors. We will gradually increase the dimension with which we work. We start from 1 and from the lower left edge of the matrix (marked in green) with a minimum dimension of 1x1.
Increase the dimension. Suppose we have no error in position G1. Then Γ1 = 0.
We must get [0 0] on the right, or at least one 0 in the first place to increase the dimension of the calculations, but in the first place is 1. We can choose a value for G1 (which is now 0) so that we get the required 0 on the right The process of selecting the value of G1 in the algorithm is optimized. We write down the two equations considered by you one more time, and also derive the third equation, which calculates G1. Colors show where it goes.
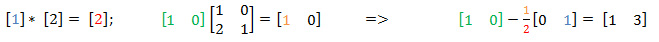
Those. G1 = 3. I remind you that the count goes to GF (7). It is also worth noting that the G1 value is temporary. During G2 calculations, it can change. We re-read the right side:
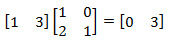
We got 0 on the right, now we increase the dimension. We assume by analogy that G2 = 0. We use the found G1 = 3.
First of all, instead of the three on the right, you need to get 0. Actions correspond to the previous ones. Next, the selection of the value of G2.
We write the new value Г2 = 2 in the main equation and again try to find the values on the right:
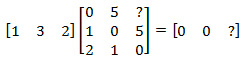
The task at this step was to get only the first zero, but by chance the second element of the matrix also turned out to be zero, i.e. the problem is solved. If it were not zero, we would once again make a selection of values (this time for both G1 and G2), increasing the dimension of the selection. If you are interested in this algorithm, here are two more examples.
So, G1 = 3, G2 = 2. Nonzero values for G1 and G2 show that there were 2 errors. We write the matrix Γ in the form of a polynomial: Γ (z) = 1 + 3x + 2x 2. The roots, taking into account the degrees of the primitive element, in which the result is 0:
Г (5 3 ) = 1 + 3 * 6 + 2 * 6 2 = 91 = 13 * 7 = 0.
Г (5 5 ) = 1 + 3 * 3 + 2 * 3 2 = 28 = 0.
This means that the errors are in positions 3 and 5.
Similarly, you can find the rest of the values to make sure that they do not give zeros:
Г => г (z j ) = (3,5,5 , 0.4.0). As you may have noticed, IDFT is used again in GF (7).
Forni error correction
At the previous stage, error positions were calculated, now it remains to find the correct values. A polynomial describing error positions: G (z) = 1 + 3x + 2x 2 . We write it in a normalized form, multiplying by 4 and using the properties of GF (7): G (z) = x 2 + 5x + 4.
Forni's method is based on Lagrange interpolation and uses the polynomials that we operated on in the Berlekamp-Messi algorithm.
The method additionally calculates those characters that are in places that are not related to the syndrome. These are the positions that correspond to the real values, however, other values are calculated for them, which are obtained from the convolution of the error syndrome and polynomial G. These calculated new values together with the syndrome form the error mask. Next, IDFT is performed and the result is a direct error that was previously summed with the transmitted codeword. It is subtracted from the received word and we get the original word transmitted. Then we perform the DFT for the transmitted codeword and finally get the information. Next, how this happens in the context of this example.
We write the error vector F (the last 4 characters are the syndrome that we constantly use, the two question marks are in the places of the information symbols, this is the error mask) and we denote each symbol with the letter: We denote the
symbols of the error locator polynomial G (z) = x2 + 5x + 4 So:
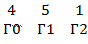
The multiplication of the polynomial Γ by the Toeplitz matrix in the previous section was, in fact, a cyclic convolution operation: if you paint the linear equations that are obtained from the matrix, you can see that the values that are taken from the syndrome (the values of the Toeplitz matrix) simply change from equation to equation in places, moving sequentially in a certain direction, and this is called a convolution. I deliberately placed the polynomials F and G on top of each other at the beginning of this paragraph so that you can do convolutions (multiply elementwise in a certain order), moving the polynomials visually. Opening the matrix equation from the previous section and using the notation for the polynomials F and Γ introduced just now:
Г0 * F4 + Г1 * F3 + Г2 * F2 = 0
Г0 * F5 + Г1 * F4 + Г2 * F3 = 0
Previously, the convolution was performed only for the syndrome, in the Forni method it is necessary to make convolutions for F0 and F1, and then find their values:
Г0 * F3 + Г1 * F2 + Г2 * F1 = 0
Г0 * F2 + Г1 * F1 + Г2 * F0 = 0
F0 = -G0 * F3 - G1 * F2 = 0
F1 = -G0 * F2 - G1 * F1 = 6
That is, F = (6,0,2,1,0,5). We carry out IDFT, since the error was summed up with a word that was in the IDFT encoded form: f = (0,0,0,2,0,6).
Subtract the error f from the resulting codeword cf: (4,1,0,4,5,5) - (0,0,0,2,0,6) = s (4,1,0,2,5,6 )
Let's make a DFT for this word: с (4,1,0,2,5,6) => С = (3,1,0,0,0,0). And here are our characters 3 and 1, which needed to be transmitted.
Conclusion
Usually, extended Reed-Solomon codes are used, that is, the Galois field is a power of two (GF (2 m )), for example, encoding bytes of information. The work algorithms are similar to those that are analyzed in this article.
There are many varieties of the algorithm depending on the application, as well as depending on the age of each particular variety and the development company. The younger the algorithm, the harder it is.
Many devices also use predefined error tables. When using Galois arithmetic, a finite number of possible errors are obtained. This property is used to reduce the number of calculations. Here, if the syndrome turns out to be non-zero, it is simply compared with a table of possible erroneous syndromes.
For many, a coding theory course is often one of the most difficult. I would be glad if this article helps someone understand this topic faster.