Alternative Tic Tac Toe
- Transfer
Once, at a picnic, I noticed mathematicians crowding around a game of which I expected the least interest: tic-tac-toe.
You yourself may have noticed that the game of tic-tac-toe is deadly boring. There is no place for a creative idea or sudden illumination in it. Good players always draw. The game inevitably goes something like this: But the maths at the picnic played a more sophisticated version of the game. In each of the cells in a square field, they drew a smaller field: As I watched, I noticed the basic rules: 1. Each move is made in one of the small fields. 2. Having reached the location of three identical figures in a row in a small field, this field wins. 3. To win the game, you need to win in three small fields in a row.
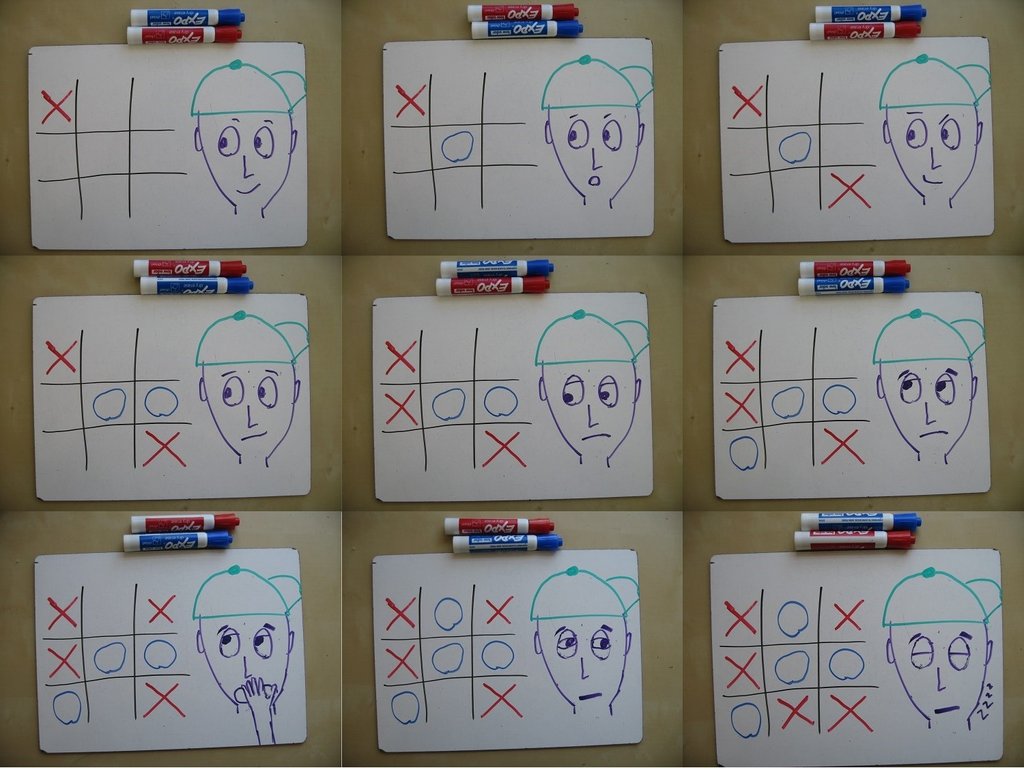



But to understand the most important rule, it took me a while:
The player does not select one of the nine small fields in which he wants to go. The choice is determined by the previous move of your opponent. A cell in a small field, into which he went, is that small field in which you have to make a move. (And the cell you go to, in turn, determines what small field your opponent will go to.) For example, if I go down here ...

You will make your next move here ...

This gives the game an element of strategy. You cannot afford to focus on a small field. You have to consider where your move will send your opponent, and where his next move will send you, and so on.
The result looks very unusual. Players can move randomly, easily skipping designs in two and three identical pieces in a row. But there is an order in this madness - they think over their moves in advance, remembering the possibility of sending an opponent to untouched real estate. This, in general, is much more interesting than regular tic-tac-toe.
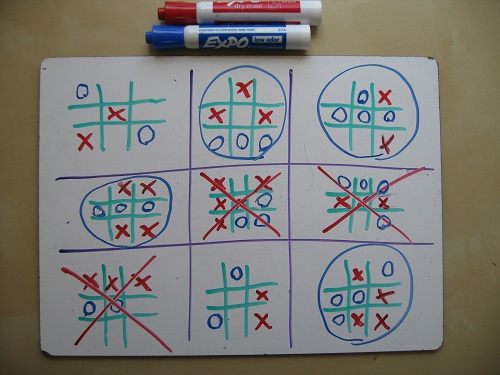
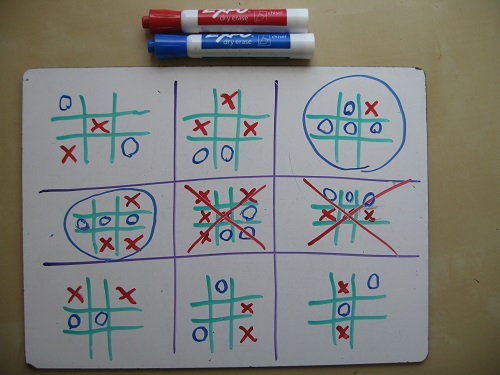
A couple of conventions are needed:
1. What if my opponent sends me to a small field in which a victory has already been won? This is an unfortunate situation. If there are empty cells left, you have to choose one of them. Although you will not be able to influence the outcome of the game in this field, you will at least determine where your opponent will go.

2. What if my opponent sends me to the completed field? In this case, please accept our congratulations - you can choose any of the fields for the move. (This means that you should avoid sending your opponent to the filled field!)
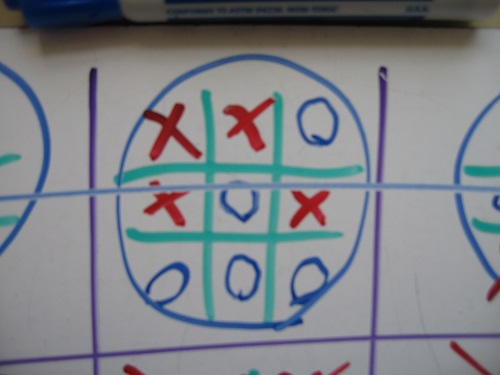
When I see my students playing tic-tac-toe, I restrain the desire to roll my eyes and show them this game. You can bet that the game develops mathematical skills (deductive reasoning, conditional thinking, the geometric idea of similarity), but what's the difference? In any case, the game is good.
And the last: I developed a strategy, which I modestly called Gambit Orlin. You start by capturing the most central cell.

Your opponent will have to put a toe in any of the other cells.

Go to the center again.

Tac toe begins to form a row. Go to the center again. Your opponent forms a winning row, laughing at your stupidity. Go to the center again. Opponent sees the trick that you went ... Again, go to the center. Your opponent is reluctant to understand that it is impossible to stop you. At the end, the crosses at the cost of sacrifice of the central field have the best position in the other eight. This is by no means an ideal strategy. It stimulates the loss of the central field without a fight. But the forced useless accumulation of so many tokens on one field allows the tic to get the upper hand throughout the rest of the game. In a word, these are alternative tic-tac-toe. Play! Let me know how you are doing.





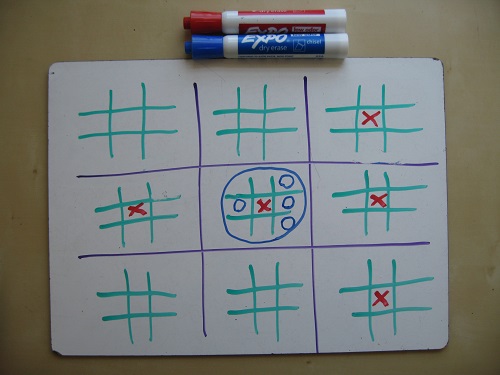
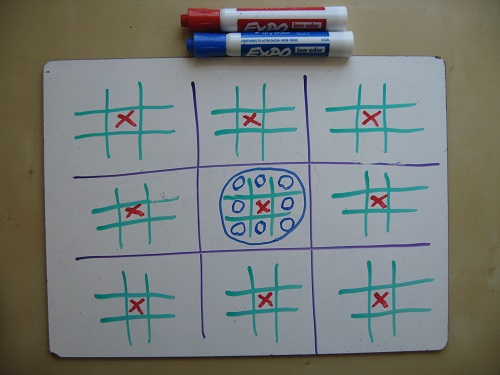
Update June 18: A frequent (and not stupid) question: “What if there is a draw in one of the small fields?” It seems that there are two options:
1. The field is considered neither a cross nor a zero. (So I play.)
2. The field is considered both for a cross, and for a zero. (This will help avoid draws, although it can lead to a strange draw when you and your opponent win at the same time.)
I believe that each option works. Just make sure that you and your opponent agree before the game starts, as this affects the strategy.
Translator’s note: there is already an implementation of this game for the Android platform .
You yourself may have noticed that the game of tic-tac-toe is deadly boring. There is no place for a creative idea or sudden illumination in it. Good players always draw. The game inevitably goes something like this: But the maths at the picnic played a more sophisticated version of the game. In each of the cells in a square field, they drew a smaller field: As I watched, I noticed the basic rules: 1. Each move is made in one of the small fields. 2. Having reached the location of three identical figures in a row in a small field, this field wins. 3. To win the game, you need to win in three small fields in a row.





But to understand the most important rule, it took me a while:
The player does not select one of the nine small fields in which he wants to go. The choice is determined by the previous move of your opponent. A cell in a small field, into which he went, is that small field in which you have to make a move. (And the cell you go to, in turn, determines what small field your opponent will go to.) For example, if I go down here ...

You will make your next move here ...

This gives the game an element of strategy. You cannot afford to focus on a small field. You have to consider where your move will send your opponent, and where his next move will send you, and so on.
The result looks very unusual. Players can move randomly, easily skipping designs in two and three identical pieces in a row. But there is an order in this madness - they think over their moves in advance, remembering the possibility of sending an opponent to untouched real estate. This, in general, is much more interesting than regular tic-tac-toe.

A couple of conventions are needed:
1. What if my opponent sends me to a small field in which a victory has already been won? This is an unfortunate situation. If there are empty cells left, you have to choose one of them. Although you will not be able to influence the outcome of the game in this field, you will at least determine where your opponent will go.

2. What if my opponent sends me to the completed field? In this case, please accept our congratulations - you can choose any of the fields for the move. (This means that you should avoid sending your opponent to the filled field!)

When I see my students playing tic-tac-toe, I restrain the desire to roll my eyes and show them this game. You can bet that the game develops mathematical skills (deductive reasoning, conditional thinking, the geometric idea of similarity), but what's the difference? In any case, the game is good.
And the last: I developed a strategy, which I modestly called Gambit Orlin. You start by capturing the most central cell.

Your opponent will have to put a toe in any of the other cells.

Go to the center again.

Tac toe begins to form a row. Go to the center again. Your opponent forms a winning row, laughing at your stupidity. Go to the center again. Opponent sees the trick that you went ... Again, go to the center. Your opponent is reluctant to understand that it is impossible to stop you. At the end, the crosses at the cost of sacrifice of the central field have the best position in the other eight. This is by no means an ideal strategy. It stimulates the loss of the central field without a fight. But the forced useless accumulation of so many tokens on one field allows the tic to get the upper hand throughout the rest of the game. In a word, these are alternative tic-tac-toe. Play! Let me know how you are doing.







Update June 18: A frequent (and not stupid) question: “What if there is a draw in one of the small fields?” It seems that there are two options:
1. The field is considered neither a cross nor a zero. (So I play.)
2. The field is considered both for a cross, and for a zero. (This will help avoid draws, although it can lead to a strange draw when you and your opponent win at the same time.)
I believe that each option works. Just make sure that you and your opponent agree before the game starts, as this affects the strategy.
Translator’s note: there is already an implementation of this game for the Android platform .
