Spatial hashing for the little ones

Spatial hashing is a simple technique that is used in databases, physical and graphic engines, particle simulations, and generally wherever you need to quickly find something. In short, the bottom line is that we break the space with objects into cells and put the objects in them. Then, instead of searching by value, we quickly search by hash.

Suppose you have several objects and you need to find out if there are any collisions between them. The simplest solution is to calculate the distance from each object to all other objects. However, with this approach, the number of necessary calculations grows too fast. If a dozen objects have to do a hundred checks, then a hundred objects come out already tens of thousands of checks. This is the infamous quadratic complexity of the algorithm.

Hereinafter, pseudo-code is used, suspiciously very similar to C #, but this is just an illusion. This code is at the end of the article.

// В каждом объекте
foreach (var obj in objects)
{
    if (Distance(this.position, obj.position) < t)
    {
        // Нашли одного соседа
    }
}

You can improve the situation if you break the space using the grid. Then each object will fall into some cell of the grid and it will be quite simple to find neighboring cells to check their fullness. For example, we can be sure that two objects did not collide if they were separated by at least one cell.



The grid is already good, but there is a problem with updating the grid. Constant sifting of coordinates in cells can work well in two dimensions, but in three it already starts to slow down. We can step further and reduce the multidimensional search space to one-dimensional using hashing. Hashing will allow us to fill cells faster and search them. How does this work?

Hashingthis is the process of converting a large amount of data to a fixed one, and a small difference in the source data results in a large difference in a fixed one. This is essentially lossy compression. We can assign an identifier to each cell, and when we compress the coordinates of the objects, drawing an analogy with the pictures, lower their resolution, then we automatically get the coordinates of the desired cell. Filling all the cells in this way, we can then easily get objects in the vicinity of any coordinates. We just hash the coordinates and get the identifier of the cell with the objects.

What might a hash function look like for a two-dimensional grid of a fixed size? For example as follows:

hashId = (Math.Floor(position.x / сellSize)) + (Math.Floor(position.y / сellSize)) * width;

We divide the x-coordinate by the cell size and cut off the fractional part, then do the same with the y-coordinate and multiply by the width of the grid. It turns out a one-dimensional array as in the picture below.



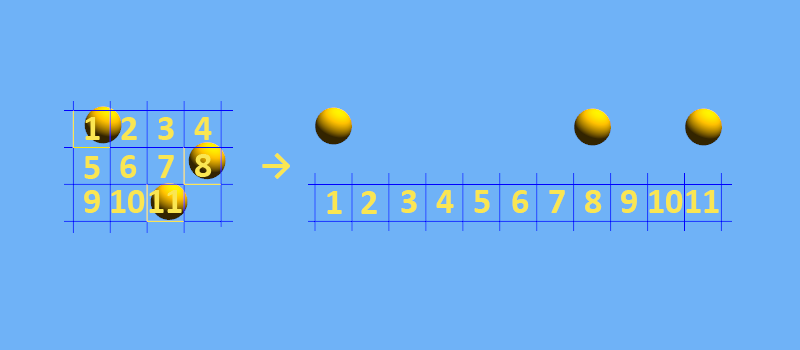
In fact, we have the same grid as before, but the search is faster due to the simplification of calculations. True, they are simplified due to the appearance of collisions, when the coordinate hash of a very distant object can coincide with the coordinate hash of a close one. Therefore, it is important to choose a hash function with a good distribution and an acceptable collision frequency. Read more on Wikipedia. I’d better show how you can implement a three-dimensional spatial hash in practice.

Add a little about hashes
What is faster to calculate 2 * 3.14 or 2 * 3.1415926535897932384626433832795028841971 ...? Of course, the first. We get a less accurate result, but who cares? Similarly with hashes. We simplify calculations, lose accuracy, but with high probability we still get a result that suits us. This is the hash chip and the source of their strength.

Let's start with the most important thing - hash functions for three-dimensional coordinates. In a very eventful article on the Nvidia website they offer the following option:

GLuint hash = ((GLuint)(pos.x / CELLSIZE) << XSHIFT) | ((GLuint)(pos.y / CELLSIZE) << YSHIFT) | ((GLuint)(pos.z / CELLSIZE) << ZSHIFT);

We take the coordinate along each axis, divide by the size of the cell, apply a bit shift and OR the results between them. The authors of the article do not specify what magnitude the shift should be, moreover, bit math is not entirely “for the smallest”. There is a function a little easier described in this publication . If you translate it into code, you get something like that:

hash = (Floor(pos.x / cellSize) * 73856093) ^ (Floor(pos.y / cellSize) * 19349663) ^ (Floor(pos.z / cellSize) * 83492791);

Find the cell coordinates on each axis, multiply by a large prime number and XOR. Honestly, not much easier, but at least without unknown shifts.

To work with a spatial hash, it is convenient to have two containers: one for storing objects in cells, the other for storing object cell numbers. Hashtables work most quickly as main containers, they are dictionaries, they are also hashmaps or as they are also called in your favorite language. In one of them, we get the stored object by the hash key, and the cell number in the other by the object key. Together, these two containers allow you to quickly find neighbors and check the fullness of the cells.

private Dictionary> dict;
private Dictionary objects;

How does working with these containers look like? We insert objects using two parameters: coordinates and the object itself.

public void Insert(Vector3 vector, T obj)
{
    var key = Key(vector);
    if (dict.ContainsKey(key))
    {
        dict[key].Add(obj);
    }
    else
    {
        dict[key] = new List { obj };
    }
    objects[obj] = key;
}

Hash the coordinates, check for the key in the dictionary, cram the object with the key and the key with the object. When we need to update the coordinates, we remove the object from the old cell and insert it into the new one.

public void UpdatePosition(Vector3 vector, T obj)
{
    if (objects.ContainsKey(obj))
    {
        dict[objects[obj]].Remove(obj);
    }
    Insert(vector, obj);
}

If too many objects are updated at a time, then it is easier to clear all dictionaries and re-fill them each time.

public void Clear()
{
    var keys = dict.Keys.ToArray();
    for (var i = 0; i < keys.Length; i++)
        dict[keys[i]].Clear();
    objects.Clear();
}

That's it, the full class code is presented below. It uses Vector3 from the Unity engine, but the code can easily be adapted for XNA or another framework. The function of the hash uses a certain “quick rounding”, I can not vouch for its work.


In the interactive demo, follow this link to see how the hash space is distributed. The coordinates of the yellow ball are hashed by a timer, after which it moves to a random point inside the sphere. Yellow cubes indicate the coordinates that fall into the same cell. The blue keys indicate already created keys so that you can look at the process of filling the memory. The mouse can be rotated.

Sources on GitHub | Online version for owners of Unity Web Player

Interesting related links

http://www.cs.ucf.edu/~jmesit/publications/scsc%202005.pdf
http://www.beosil.com/download/CollisionDetectionHashing_VMV03.pdf
http://http.developer.nvidia.com/GPUGems3 /gpugems3_ch32.html