Experimental data approximation experience
The other day, there was a task to program a device for measuring air flow rate. As a measuring element - the sensor is not clear which manufacturer, there are no characteristics or any adequate parameters. There was no choice, it was necessary to remove the calibration characteristics and display the transfer function “ADC-stream readings”.
Since the sensor, like almost any measuring instrument, is very sensitive to temperature, I needed to remove a family of characteristics (minimum 3) for different temperatures.
The data can be entered into MathCad in various ways, I preferred to do this in the form of transposed row vectors:

After that, you need to use a “strong-willed" solution to set the type of the approximating function and to approximate each calibration characteristic. So, my characteristics are successfully approximated by a polynomial of the third degree, using the linfit function, which searches for a solution in the form of linear combinations of arbitrary functions, I got coefficients for three polynomials:

To see how “successful” the experimental data are modeled by the obtained polynomial, you can plot:

Now, in order to introduce a temperature correction, one needs to find the dependence of each polynomial coefficient on temperature, i.e. do the above only for the odds. The experimental data will now be the coefficients and temperature values themselves. I really wanted that the temperature dependence was linear, it is possible to use the linfit function unnecessarily for linear approximation, but still:

Finally, the desired dependence appears in the following form:
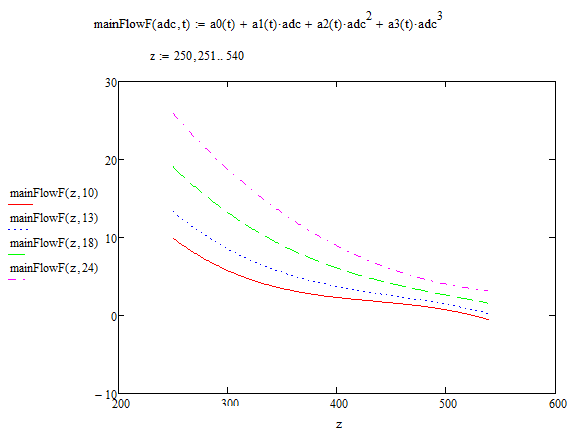
Commenting on the result, I note that it turned out not very successfully, frankly disgusting. Characteristics were initially poorly shot, the lack of a normal stand affected. And in general, the calibration task is far from amateurish; you won’t do it on the knee. But I wanted to talk about the approach.
Since the sensor, like almost any measuring instrument, is very sensitive to temperature, I needed to remove a family of characteristics (minimum 3) for different temperatures.
The data can be entered into MathCad in various ways, I preferred to do this in the form of transposed row vectors:

After that, you need to use a “strong-willed" solution to set the type of the approximating function and to approximate each calibration characteristic. So, my characteristics are successfully approximated by a polynomial of the third degree, using the linfit function, which searches for a solution in the form of linear combinations of arbitrary functions, I got coefficients for three polynomials:

To see how “successful” the experimental data are modeled by the obtained polynomial, you can plot:

Now, in order to introduce a temperature correction, one needs to find the dependence of each polynomial coefficient on temperature, i.e. do the above only for the odds. The experimental data will now be the coefficients and temperature values themselves. I really wanted that the temperature dependence was linear, it is possible to use the linfit function unnecessarily for linear approximation, but still:

Finally, the desired dependence appears in the following form:

Commenting on the result, I note that it turned out not very successfully, frankly disgusting. Characteristics were initially poorly shot, the lack of a normal stand affected. And in general, the calibration task is far from amateurish; you won’t do it on the knee. But I wanted to talk about the approach.
