Briefly about hydrodynamics: energy conservation
Once again, I apologize for the slow writing of posts in the planned series. This time, the reason for the delay is objective, in the form of a conference in Vienna, although it has a significant subjective component in the form of its own participation there and some bureaucratic aspects of preparation and payment.
This post discusses the laws of energy conservation in an ideal and viscous fluid. They are obviously necessary for a complete description of the motion, however, in the isothermal case there is no heat transfer as such, and therefore it is sufficient to use the Navier-Stokes equation and the continuity equation to describe it. I hope this post will be the last of the rather abstract posts that describe the general theory and are not practically tied to specific problem statements.
Previous Posts:
Briefly about hydrodynamics: do you remember how it all began?
Briefly about hydrodynamics: equations of motion
I will try to reduce the number of calculations, because they are, of course, important, but the results in the form of finite equations are more important.
So energy conservation. The approach to the description is absolutely standard - we introduce a certain quantity, find which mechanisms are responsible for its change and write the conservation law first in integral form, and then, reducing all surface integrals to volume integrals by the Gauss theorem, in differential.
The energy of a liquid in classical hydrodynamics, which also does not take into account such an effect as electrical conductivity and the corresponding interaction with external and internal electromagnetic fields, consists of internal and kinetic energy. It is equal to such an integral: Energy can
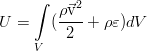
vary within our volume V due to its simple flow along with the fluid flow, the work of pressure forces from the external fluid elements and the work of external forces (shown below on the example of gravity):
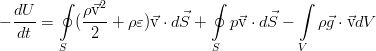
In an ideal fluid there is no friction, and therefore there is no energy dissipation due to viscosity. In addition, heat conduction processes are neglected here, which is also inherent in an ideal fluid as the absence of another mechanism of energy dissipation. In differential form, the law of conservation of total energy looks like this:
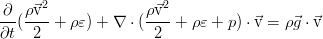
However, it can be safely simplified. Using the Euler equation (see the previous post ), scalarly multiplied by speed, we can distinguish the following part from the obtained conservation law:
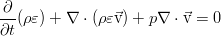
And this is already being converted to an even simpler form:
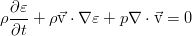
Here we can recall thermodynamics. The first law of thermodynamics (marked with - for the specific volume of liquid, i.e., a volume whose mass is equal to unity):
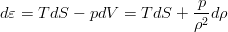
allows you to quite clearly associate the derivatives of energy, entropy and density (as the reciprocal of the volume value). Using this relationship of the differentials of the quantities in the equation for energy:

as well as the law of conservation of mass, we obtain another equation that describes the evolution of entropy in a liquid:
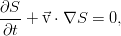
In a moving reference frame attached to that element of the liquid for which this is all written, the equation simplifies even more:
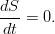
That is, the entropy of an individual arbitrary liquid particle (in an ideal liquid) is preserved. Entropy is simply passively carried by the flow, simultaneously linking the pressure and density of the medium with the equation of state.
Now we take into account viscous and heat-conducting dissipation. In integral form, they are represented by a pair of additional terms in the conservation law:

They describe the work of viscous friction forces at the boundary of a fluid element and the heat flux through the boundary. In differential form, the equation of conservation of total energy:
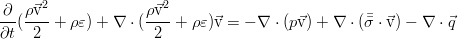
After performing a series of operations on this relation using the momentum transfer equation in general form (for an arbitrary tensor of viscous stresses) and the continuity equation (namely, multiplying the law of conservation of mass by half the speed square, the law of conservation of momentum by velocity, adding them together and subtracting the total from the equation for the total energy), we will get rid of the terms with kinetic energy:
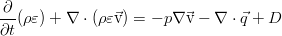
Here a dissipative function arises, equal to the double convolution of the tensor of viscous stresses and the tensor, which is sometimes referred to as the velocity gradient:
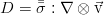
Applying the mass balance equation here and the first law of thermodynamics, similarly to the above, we arrive at the entropy balance equation:
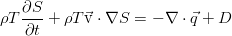
It can be seen that it differs from equations in an ideal fluid are only a nonzero right-hand side. For an incompressible fluid, we can safely pass from entropy to a more tangible value, that is, to temperature, using the definition of heat capacity at constant pressure:
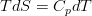
Finally, the dissipative function can be neglected, since it describes the release due to internal friction, and therefore it is significant only in liquids with very high viscosities, and for the heat flux use the Fourier law of heat conduction, which allows expressing it in terms of temperature:
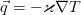
As a result, we obtain the heat equation of an incompressible viscous fluid:
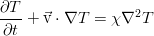
According to it, the temperature of the fluid element changes due to direct convective transport with a fluid flow, as well as due to the quite ordinary mechanism of molecular thermal conductivity (right side).
Actually, with the description of the convection problem on the hub , this whole hydrodynamic “booth” began. So, we look at a jar of incompressible viscous liquid, for example, water. Its movement in the case of an inhomogeneous temperature in the volume is described by three equations:
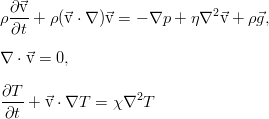
In the general case, this system also includes the equation of state that relates density, pressure and temperature. However, then the liquid can no longer be considered incompressible. Practice, however (and mathematics), shows that with sufficient accuracy one can take the density constant everywhere, except for the term with gravity. Moreover, it is enough to limit ourselves to a linear expansion in temperature:
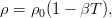
Immediately, we note that here is no longer the absolute temperature, but already a deviation from a certain “zero” level, at which the density is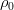 . The heat equation allows us to write this way, since it is linear and is invariant to such shifts. We can distinguish the temperature-independent part (hydrostatic gradient) in the gravity term and hide it in pressure:
. The heat equation allows us to write this way, since it is linear and is invariant to such shifts. We can distinguish the temperature-independent part (hydrostatic gradient) in the gravity term and hide it in pressure:

And then we come to the convection equations in the Boussinesq approximation:
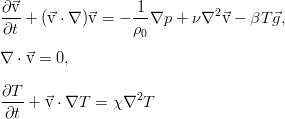
This model is practically common in the study of convective phenomena, and on its basis a huge amount of the most results of different significance. In particular, in problems of stability of fluid equilibrium and others.
I will digress a little from the topic, although I understand perfectly well that this can only ignite an unnecessary and distracting discussion.
Do you know what surprised you in the comments on the previous post? The fact that readers pay a lot of attention to the issue of mathematical rigor of the calculations, which, in general, is not enough. Hydrodynamics was created by Euler and Navier during the reign of French materialism, when the rigorous results of analytical mechanics seemed to describe the whole world. But the level of severity of these results is what it could be in those days, in the barely just created by Newton and other differential calculus, and not higher. And he remained so to this day, and the mathematical rigor of hydrodynamics is the same. In practice, this is the last classical field of science, which still has unresolved fundamental problems. Perhaps they have not been resolved precisely because they are formulated in that old, not very developed and not rich in significant means language. I remember there are some developments in mathematics, where the apparatus is applied to the Navier-Stokes equations, be mindful of Dirac bispinors and gamma matrices (the basis of quantum field theory) or worse. But they are still separate and almost unknown.
Personally, I assume that the development of the apparatus for solving the Navier-Stokes equations has simply not yet taken place. After all, as you know, these equations perfectly describe both ordered laminar flows and the chaos of turbulence. And in the equations for this all you need to do is change one control parameter. As in non-linear systems (a la Lorentz system), which also do not have common analytical solutions, and, in general, a specific detailed analysis of the properties of solutions, namely, as mathematical functions. Much on the level of behavior - here is chaos, there is ordering, there is synchronization, there is the influence of the parameter, and the transition, apparently, happens in this way. But neither the smoothness of the solutions, nor their existence is a question in such problems, unlike Navier-Stokes. After all, we still practically do not know whether their general smooth solutions exist at all.
Seeing things like “nabla is a 1-form” in the comments, I first thought hard about whether I had missed something in my education. Yes, about various kinds of n-forms in my courses mentioned(but no more) in one semester special course called group theory in physics, from which, however, much could not be learned due to the lack of a serious structured presentation. But one never has to speculate whether the nabla is a vector or not. In physics, which does not concern significantly mathematical problems of the level of, say, the general theory of relativity and the inherently necessary differential geometry for it, nabla has always been almost a vector. Of course, not quite ordinary, not commuting with them and possessing a number of other properties. A simple, in general, even an ordinary operator that shows which component of the vector and how we will differentiate. Just a toolwhich we know how to use within specified limits and realize that it is necessary to check its suitability when going beyond the border of a familiar area, even, for example, when moving from Cartesian coordinates to the same spherical ones.
Sometimes you can spend too much time understanding the structure of the hammer, but you really can’t really learn how to hammer nails with it. For example, why it has such a shape, why different hammers have a different shape, and then start digging deeper - why metal shines, and a wooden handle does not, etc. But from this understanding the essence of the most frequent use of the hammer will not change. They will hammer nails, align the metal on the mandrel, etc. - they will still be knocked, preferably not on the fingers.
At this level is my personal acquaintance with the apparatus of quantum electrodynamics. According to the principle - I remember that something passed. Moreover, even the training manual was published with the teacher of this subject last year, but somehow it is still on the sidelines - I’m not doing it.
The next post will be devoted to stability problems for equilibrium and stationary flow. Once again, we will see that even the simplest problems of hydrodynamics cannot be solved analytically in full, and therefore we have to apply many different, at first glance very controversial, but at the same time perfectly working and well-grounded methods. I hope that we will already be able to move from abstract to more tangible things.
This post discusses the laws of energy conservation in an ideal and viscous fluid. They are obviously necessary for a complete description of the motion, however, in the isothermal case there is no heat transfer as such, and therefore it is sufficient to use the Navier-Stokes equation and the continuity equation to describe it. I hope this post will be the last of the rather abstract posts that describe the general theory and are not practically tied to specific problem statements.
Previous Posts:
Briefly about hydrodynamics: do you remember how it all began?
Briefly about hydrodynamics: equations of motion
I will try to reduce the number of calculations, because they are, of course, important, but the results in the form of finite equations are more important.
Energy transfer in a perfect fluid
So energy conservation. The approach to the description is absolutely standard - we introduce a certain quantity, find which mechanisms are responsible for its change and write the conservation law first in integral form, and then, reducing all surface integrals to volume integrals by the Gauss theorem, in differential.
The energy of a liquid in classical hydrodynamics, which also does not take into account such an effect as electrical conductivity and the corresponding interaction with external and internal electromagnetic fields, consists of internal and kinetic energy. It is equal to such an integral: Energy can
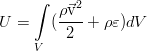
vary within our volume V due to its simple flow along with the fluid flow, the work of pressure forces from the external fluid elements and the work of external forces (shown below on the example of gravity):
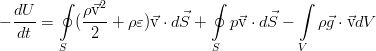
In an ideal fluid there is no friction, and therefore there is no energy dissipation due to viscosity. In addition, heat conduction processes are neglected here, which is also inherent in an ideal fluid as the absence of another mechanism of energy dissipation. In differential form, the law of conservation of total energy looks like this:
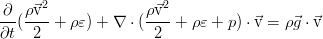
However, it can be safely simplified. Using the Euler equation (see the previous post ), scalarly multiplied by speed, we can distinguish the following part from the obtained conservation law:
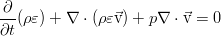
And this is already being converted to an even simpler form:
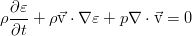
Here we can recall thermodynamics. The first law of thermodynamics (marked with - for the specific volume of liquid, i.e., a volume whose mass is equal to unity):
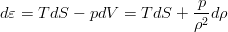
allows you to quite clearly associate the derivatives of energy, entropy and density (as the reciprocal of the volume value). Using this relationship of the differentials of the quantities in the equation for energy:

as well as the law of conservation of mass, we obtain another equation that describes the evolution of entropy in a liquid:
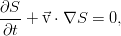
In a moving reference frame attached to that element of the liquid for which this is all written, the equation simplifies even more:
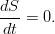
That is, the entropy of an individual arbitrary liquid particle (in an ideal liquid) is preserved. Entropy is simply passively carried by the flow, simultaneously linking the pressure and density of the medium with the equation of state.
Accounting for viscosity. Heat equation
Now we take into account viscous and heat-conducting dissipation. In integral form, they are represented by a pair of additional terms in the conservation law:

They describe the work of viscous friction forces at the boundary of a fluid element and the heat flux through the boundary. In differential form, the equation of conservation of total energy:
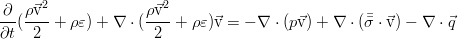
After performing a series of operations on this relation using the momentum transfer equation in general form (for an arbitrary tensor of viscous stresses) and the continuity equation (namely, multiplying the law of conservation of mass by half the speed square, the law of conservation of momentum by velocity, adding them together and subtracting the total from the equation for the total energy), we will get rid of the terms with kinetic energy:
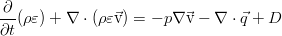
Here a dissipative function arises, equal to the double convolution of the tensor of viscous stresses and the tensor, which is sometimes referred to as the velocity gradient:
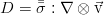
Applying the mass balance equation here and the first law of thermodynamics, similarly to the above, we arrive at the entropy balance equation:
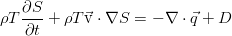
It can be seen that it differs from equations in an ideal fluid are only a nonzero right-hand side. For an incompressible fluid, we can safely pass from entropy to a more tangible value, that is, to temperature, using the definition of heat capacity at constant pressure:
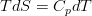
Finally, the dissipative function can be neglected, since it describes the release due to internal friction, and therefore it is significant only in liquids with very high viscosities, and for the heat flux use the Fourier law of heat conduction, which allows expressing it in terms of temperature:
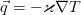
As a result, we obtain the heat equation of an incompressible viscous fluid:
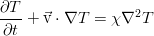
According to it, the temperature of the fluid element changes due to direct convective transport with a fluid flow, as well as due to the quite ordinary mechanism of molecular thermal conductivity (right side).
Convection. Boussinesq approaching
Actually, with the description of the convection problem on the hub , this whole hydrodynamic “booth” began. So, we look at a jar of incompressible viscous liquid, for example, water. Its movement in the case of an inhomogeneous temperature in the volume is described by three equations:
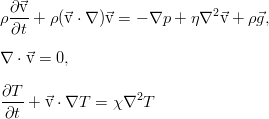
In the general case, this system also includes the equation of state that relates density, pressure and temperature. However, then the liquid can no longer be considered incompressible. Practice, however (and mathematics), shows that with sufficient accuracy one can take the density constant everywhere, except for the term with gravity. Moreover, it is enough to limit ourselves to a linear expansion in temperature:
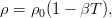
Immediately, we note that here is no longer the absolute temperature, but already a deviation from a certain “zero” level, at which the density is
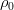 . The heat equation allows us to write this way, since it is linear and is invariant to such shifts. We can distinguish the temperature-independent part (hydrostatic gradient) in the gravity term and hide it in pressure:
. The heat equation allows us to write this way, since it is linear and is invariant to such shifts. We can distinguish the temperature-independent part (hydrostatic gradient) in the gravity term and hide it in pressure: 
And then we come to the convection equations in the Boussinesq approximation:
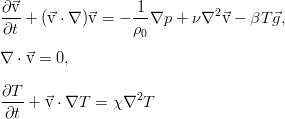
This model is practically common in the study of convective phenomena, and on its basis a huge amount of the most results of different significance. In particular, in problems of stability of fluid equilibrium and others.
Tool issue
I will digress a little from the topic, although I understand perfectly well that this can only ignite an unnecessary and distracting discussion.
Do you know what surprised you in the comments on the previous post? The fact that readers pay a lot of attention to the issue of mathematical rigor of the calculations, which, in general, is not enough. Hydrodynamics was created by Euler and Navier during the reign of French materialism, when the rigorous results of analytical mechanics seemed to describe the whole world. But the level of severity of these results is what it could be in those days, in the barely just created by Newton and other differential calculus, and not higher. And he remained so to this day, and the mathematical rigor of hydrodynamics is the same. In practice, this is the last classical field of science, which still has unresolved fundamental problems. Perhaps they have not been resolved precisely because they are formulated in that old, not very developed and not rich in significant means language. I remember there are some developments in mathematics, where the apparatus is applied to the Navier-Stokes equations, be mindful of Dirac bispinors and gamma matrices (the basis of quantum field theory) or worse. But they are still separate and almost unknown.
Personally, I assume that the development of the apparatus for solving the Navier-Stokes equations has simply not yet taken place. After all, as you know, these equations perfectly describe both ordered laminar flows and the chaos of turbulence. And in the equations for this all you need to do is change one control parameter. As in non-linear systems (a la Lorentz system), which also do not have common analytical solutions, and, in general, a specific detailed analysis of the properties of solutions, namely, as mathematical functions. Much on the level of behavior - here is chaos, there is ordering, there is synchronization, there is the influence of the parameter, and the transition, apparently, happens in this way. But neither the smoothness of the solutions, nor their existence is a question in such problems, unlike Navier-Stokes. After all, we still practically do not know whether their general smooth solutions exist at all.
Seeing things like “nabla is a 1-form” in the comments, I first thought hard about whether I had missed something in my education. Yes, about various kinds of n-forms in my courses mentioned(but no more) in one semester special course called group theory in physics, from which, however, much could not be learned due to the lack of a serious structured presentation. But one never has to speculate whether the nabla is a vector or not. In physics, which does not concern significantly mathematical problems of the level of, say, the general theory of relativity and the inherently necessary differential geometry for it, nabla has always been almost a vector. Of course, not quite ordinary, not commuting with them and possessing a number of other properties. A simple, in general, even an ordinary operator that shows which component of the vector and how we will differentiate. Just a toolwhich we know how to use within specified limits and realize that it is necessary to check its suitability when going beyond the border of a familiar area, even, for example, when moving from Cartesian coordinates to the same spherical ones.
Sometimes you can spend too much time understanding the structure of the hammer, but you really can’t really learn how to hammer nails with it. For example, why it has such a shape, why different hammers have a different shape, and then start digging deeper - why metal shines, and a wooden handle does not, etc. But from this understanding the essence of the most frequent use of the hammer will not change. They will hammer nails, align the metal on the mandrel, etc. - they will still be knocked, preferably not on the fingers.
At this level is my personal acquaintance with the apparatus of quantum electrodynamics. According to the principle - I remember that something passed. Moreover, even the training manual was published with the teacher of this subject last year, but somehow it is still on the sidelines - I’m not doing it.
Further
The next post will be devoted to stability problems for equilibrium and stationary flow. Once again, we will see that even the simplest problems of hydrodynamics cannot be solved analytically in full, and therefore we have to apply many different, at first glance very controversial, but at the same time perfectly working and well-grounded methods. I hope that we will already be able to move from abstract to more tangible things.
Only registered users can participate in the survey. Please come in.
Continue the lecture course?
- 84.7% Yes 161
- 15.2% No 29
