Quantum mechanics for all, for nothing, and let no one go offended: part one
Hello! I would like to bring to your attention an excellent introduction to quantum mechanics, written by Eliezer Yudkovsky; perhaps he is known to you on his website lesswrong.com, which is dedicated to rationalism, prejudice, cognitive paradoxes and many other interesting things.
read the second part →
I warn you right away: this series of articles differs markedly from the traditional introduction to quantum mechanics.
First , I will not quote Richard Feynman, who once stated that "it is normal to not understand quantum mechanics, because no one understands it." This was once true, but times are changing.
I will not say: "Quantum mechanics cannot be understood, you just need to get used to it." (This quote is attributed to John von Neumann; he lived in those ancient times, when no one really understood quantum mechanics.)
You cannot end the explanation with the words “If something is not clear, it should be so.” No, that should not be . Maybe the problem is you. Maybe in your teacher. In any case, it is necessarydecide , not sit back and reassure yourself that everyone else doesn’t understand anything either.
I will not say that quantum mechanics is something strange , confusing, or inaccessible to human understanding . Yes, it is counterintuitive - but this is only a disaster for our intuition. Quantum mechanics arose long before the sun, planet Earth, or human civilization. She's not going to change for you. In general, there are no discouraging facts ; there are only theories discouraged by facts ; and if the theory does not coincide with practice, it does not honor her.
It is always worth considering reality as a completely ordinary thing. Since the beginning of time, nothing unusual has happened in the universe .
Our goal is to learn how to feel at home in this quantum world. Because we are already at home.
Throughout this cycle, I will talk about quantum mechanics as the most ordinary theory; and where the intuitive view of the world does not coincide with it, I will ridicule intuition for the mismatch of reality.
Secondly , I am not going to follow the traditional order of studying quantum mechanics, copying the order in which it was discovered.
Usually it all starts with the story that matter sometimes behaves like a bunch of small billiard balls colliding with each other, and sometimes like waves on the surface of a pool. This is followed by several examples illustrating both views of matter.
Previously, when all this was just beginning and no one had the slightest idea about the mathematical foundations of physics, scientists seriously believed that everything consists of atoms that behave like billiard balls. And then they began to believe that everything consists of waves. And then they returned to the billiard balls. All this led to the fact that scientists were completely confused, and only a few decades later - by the end of the nineteenth century - did they manage to put everything in its place.
If you apply thishistorical reliable approach to teaching modern students (as they do now), what naturally happened to early scientists will happen to them, namely, they will fall into complete and absolute confusion . Telling students of physics about wave-particle duality is the same as starting a chemistry course with a lecture on the four elements.
The electron does not look like a billiard ball or the crest of an ocean wave. An electron is a completely different object from a mathematical point of view, and it remains so under any circumstances . And if you persist in your desire to consider it both that and the way you prefer, I warn: you will chase after two hares - you will not catch a single one.
This is not the only reason the historical order is not the best choice. Let's follow the hypothetical process from the very beginning : people notice that they are surrounded by other animals - inside the animals, it turns out there are organs - and the organs, if you look closely, are made up of tissues - under the microscope it is clear that the tissues are made up of cells - the cells are made up of proteins, and other chemical compounds - chemical compounds are composed of atoms - atoms are made of protons, neutrons and electrons - but the latter is much easier and more intuitive animals, with which it all began, but were discovered by tens of thousands of years poses e .
Physics does not begin to go through biology. Then why should it begin with a discussion of laboratory experiments and their results, which even in the case of simple experiments are the result of many complex and complicated processes?
On the one hand, I can understand why experiment is paramount. We are talking about physics in the end.
On the other hand, giving students a sophisticated mathematical apparatus only so that they can analyze simple experience is already too much . Programmers, for example, are first taught to add two variables, and only then - to write multi-threaded applications; and do not care that the latter are "closer to real life."
Classical mechanics does not follow explicitly from quantum mechanics. Moreover, classical mechanics is at a much higher level. Compare atoms and molecules with quarks: millions of known chemicals, hundreds of chemical elements, and only six quarks. At first it is better to understand the simple, and only then move on to the complex.
Finally , I will consider quantum mechanics from a strictly realistic point of view - our world is a quantum one, our equations describe a territory, not its map, and the world we are familiar with exists implicitly in a quantum world. If there are anti-realists among my readers, pleasekeep your comments. Quantum mechanics is much more difficult to understand and imagine if you doubt its validity. I will talk about this in more detail in one of the following articles.
I think that the majority of theoretical physicists adhere to the point of view that I will present in this introduction. But you should still know that this is not the only possible point of view, and a considerable proportion of scientists doubt the fidelity of a realistic position. Although I am not going to pay attention to any other theories right now , I feel obligated to mention that they are .
To summarize , my goal is to teach you how to think as a native of the quantum world , and not as a tourist unwillingly .
Hold on tight to reality. We begin.
Look at the pic. 1. A half-silvered mirror is located at point A , and two photon detectors at points B and C.

This simple experiment at one time made scientists break their heads. The fact is that in half the cases, a photon emitted towards the mirror was detected by the first detector, and in half by the second. And scientists - attention, get ready to laugh - assumed that the mirror was either passing a photon or reflecting it.
Ha ha ha, imagine a mirror that can choose whether to pass a photon to it or not! If you can imagine it, then don’t do it anyway - otherwise you will get confused just like those scientists. The mirror behaves exactly the same in both cases.
If we tried to write a computer program simulating this experiment (and not just predicting the result), it would look something like this ...
At the beginning of the program, we declare a variable that stores a certain mathematical object - a configuration . It represents a certain description of the state of the world - in this case, “one photon flies to point A”.
In fact, the configuration is described by a complex number (I recall that complex numbers have the form (a + b i ), where a and b are real numbers, and i is an imaginary unit, i.e. such a number that i ² = -1) . Our configuration “photon flies to point A ” also corresponds to some number. Let it be (-1 + 0i ). In what follows, we will call the number corresponding to the configuration its amplitude .
We introduce two more configurations: “photon flies from A to point B ” and “photon flies from A to point C ”. We do not yet know the amplitudes of these configurations; they will be assigned values during program execution.

The amplitudes can be calculated by applying the rule according to which the mirror works to the initial configuration. Without going into details, we can assume that the rule looks like this: “multiply by 1 when the photon flies; multiply by i when the photon is reflected. " We apply the rule: the amplitude of the configuration “photon flies in B ” equals (-1 + 0 i) × i = (0 + - i ), and the amplitude of the configuration “photon flies in C ” is (-1 + 0 i ) × 1 = (-1 + 0 i ). Other configurations in fig. 1 no, so we are done.
In principle, we can consider “the first detector detects a photon” and “the second detector detects a photon” as separate configurations, but this does not change anything; their amplitudes will be equal to the amplitudes of the two previous configurations, respectively. (In fact , they still need to be multiplied by a factor equal to the distance from A to the detectors, but we just assume that all distances in our experiment are unit multipliers.)
So, here is the final state of the program:
And, perhaps:
Of course, no matter how many times we run the program, the final state will remain the same.
Now, for quite complex reasons, which I will not go into yet, there is no easy way to measure the amplitude of the configuration. The state of the program is hidden from us.
What to do?
Although we cannot measure the amplitude directly, we have something - namely, a magical measuring gizmo that can tell us the square of the amplitude module of the configuration. In other words, for the amplitude (a + b i ), the contraption will respond with the number (a² + b²).
It would be more accurate to say that the magic contraption is just an attitudesquares of modules to each other. But even this information is enough to understand what is happening inside the program and by what laws it works.
Using contraption, we can easily find out that the squares of the configuration modules “the first detector worked” and “the second detector worked” are equal. And after conducting some more complex experiments, we can also find out the ratio of the amplitudes themselves - i to 1.
By the way, what kind of magical measuring thing is this?
Well, when such experiments are carried out in real life, the magic thing is that the experiment is carried out a couple of thousand times and just counts how many times the photon was in the first detector, and how many - in the second. The ratio of these values will be the ratio of the squares of the amplitude modules.Why this will be so is another, much more complicated question. In the meantime, you can use the gizmo without understanding how and why it works. Everything has its time.
You may ask: “Why do we need a quantum theory if its predictions coincide with the predictions of the billiard theory?” There are two reasons. First, reality , no matter what you think, still obeys quantum laws - amplitudes, complex numbers and all that. And secondly, the "billiard" theory does not work for any more or less complex experiment. Want an example? You are welcome.
In fig. 2 you can see two mirrors at points B and C , and two half-mirrors at points A and D. Later I will explain why the segment DE is drawn with a dotted line; it will not affect the calculations in any way.
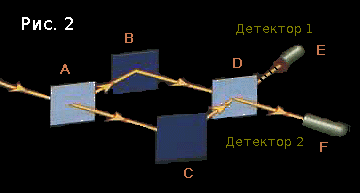
Let's apply the rules that we already know.
In the beginning we have the configuration “photon flies in A ”, its amplitude is (-1 + 0 i ).
We consider the amplitudes of the configurations “photon flies from A to B ” and “photon flies from A to C ”:
It is intuitively clear that an ordinary mirror behaves like half a half-mirror: it always reflects a photon, it always multiplies the amplitude by i . So:
It is important to understand that “from B to D ” and “from C to D ” are two different configurations. You can’t just write “the photon flies to D ”, because what happens to it next depends on the angle at which this photon arrives at D.
We consider further:
Total:
The ratio of the squares of the amplitude modules is 0 to 4; from the calculations it follows that the first detector will not work at all ! Therefore, the segment DE was drawn by the dotted line in Fig. 2.

If half-mirrors reflected or transmitted a photon randomly, both detectors would respond with approximately the same frequency. But this does not coincide with the experimental results. That's all.
You could argue: “And that’s not all! Suppose, for example, that when a mirror reflects a photon, something happens to it that it will not be reflected a second time? And, conversely, when a mirror passes a photon, it will have to reflect next time. ”
First, Occam’s razor. Do not come up with a complicated explanation if a simple one already exists (if, of course, quantum mechanics is consideredsimple ...) And secondly, I can come up with another experience that will refute this alternative theory.
We place a small opaque object between B and D so that the amplitude of the configuration “photon flies from B to D ” is always zero.
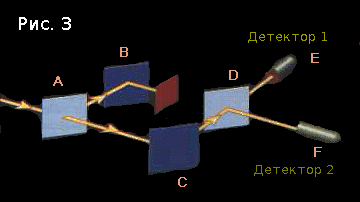
Now the amplitude of the configuration “photon flies from D to F ” is (1 + 0 i ), and the amplitude of the configuration “photon flies from D to E ” is (0 + - i ). The squares of the modules are 1. This means that in half the cases the first detector will fire, and in half the second.
It's impossibleexplain if we assume that the photon is a small billiard ball that is reflected from the mirrors.
The fact is that one cannot think of amplitude as probability. In probability theory, if event X may or may not occur, then the probability of event Z is P ( Z | X ) P ( X ) + P ( Z | ¬ X ) P (¬ X ), where all probabilities are positive. If you know that the probability Z provided that X happened is 0.5 and the probability X is 0.3, then the total probability Z is at least 0.15, regardlessfrom what will happen if X does not happen. There are no negative probabilities. Possible and impossible events cannot annul each other. And amplitudes can.

Here is an example of wrong thinking: “A photon flies to B or C , but it could fly differently, and this affects the likelihood that it will fly to E ...”
Events that did not happen have no effect on the world. The only thing that can affect the world is our imagination. “Oh my God, this car almost knocked me down,” you think, and decide to leave for the monastery so that you will never meet dangerous cars again. But really still notthe event itself , but only your imagination, contained in your brain - which you can get out, feel and put back from you to make sure that it is real.
Really everything that affects the world. (If you think this is not the case, try defining the word “real.”) The configurations and amplitudes directly affect the world, so they are also real. To say that a configuration is “something that could happen” is as strange as saying that a chair is “something that could happen”.
And what then is the configuration?
To be continued.
In fact, everything is a little more complicated than you might think after reading this article.
Each configuration describes all the particles in the universe. Amplitude is a continuous distribution over the entire space of configurations, and not discrete, as we considered today. And in fact, photons are not teleported from one place to another instantly , and each different state of the world is described by a new configuration. In the end, we get to that.
If you do not understand anything from this paragraph, do not worry, I will explain everything. Later.
read part two →
Posted by Eliezer Yudkowsky. Free and shortened (quite a bit) translation: I. Links to the originals: , .
read the second part →
Introduction to Introduction
I warn you right away: this series of articles differs markedly from the traditional introduction to quantum mechanics.
First , I will not quote Richard Feynman, who once stated that "it is normal to not understand quantum mechanics, because no one understands it." This was once true, but times are changing.
I will not say: "Quantum mechanics cannot be understood, you just need to get used to it." (This quote is attributed to John von Neumann; he lived in those ancient times, when no one really understood quantum mechanics.)
You cannot end the explanation with the words “If something is not clear, it should be so.” No, that should not be . Maybe the problem is you. Maybe in your teacher. In any case, it is necessarydecide , not sit back and reassure yourself that everyone else doesn’t understand anything either.
I will not say that quantum mechanics is something strange , confusing, or inaccessible to human understanding . Yes, it is counterintuitive - but this is only a disaster for our intuition. Quantum mechanics arose long before the sun, planet Earth, or human civilization. She's not going to change for you. In general, there are no discouraging facts ; there are only theories discouraged by facts ; and if the theory does not coincide with practice, it does not honor her.
It is always worth considering reality as a completely ordinary thing. Since the beginning of time, nothing unusual has happened in the universe .
Our goal is to learn how to feel at home in this quantum world. Because we are already at home.
Throughout this cycle, I will talk about quantum mechanics as the most ordinary theory; and where the intuitive view of the world does not coincide with it, I will ridicule intuition for the mismatch of reality.
Secondly , I am not going to follow the traditional order of studying quantum mechanics, copying the order in which it was discovered.
Usually it all starts with the story that matter sometimes behaves like a bunch of small billiard balls colliding with each other, and sometimes like waves on the surface of a pool. This is followed by several examples illustrating both views of matter.
Previously, when all this was just beginning and no one had the slightest idea about the mathematical foundations of physics, scientists seriously believed that everything consists of atoms that behave like billiard balls. And then they began to believe that everything consists of waves. And then they returned to the billiard balls. All this led to the fact that scientists were completely confused, and only a few decades later - by the end of the nineteenth century - did they manage to put everything in its place.
If you apply thishistorical reliable approach to teaching modern students (as they do now), what naturally happened to early scientists will happen to them, namely, they will fall into complete and absolute confusion . Telling students of physics about wave-particle duality is the same as starting a chemistry course with a lecture on the four elements.
The electron does not look like a billiard ball or the crest of an ocean wave. An electron is a completely different object from a mathematical point of view, and it remains so under any circumstances . And if you persist in your desire to consider it both that and the way you prefer, I warn: you will chase after two hares - you will not catch a single one.
This is not the only reason the historical order is not the best choice. Let's follow the hypothetical process from the very beginning : people notice that they are surrounded by other animals - inside the animals, it turns out there are organs - and the organs, if you look closely, are made up of tissues - under the microscope it is clear that the tissues are made up of cells - the cells are made up of proteins, and other chemical compounds - chemical compounds are composed of atoms - atoms are made of protons, neutrons and electrons - but the latter is much easier and more intuitive animals, with which it all began, but were discovered by tens of thousands of years poses e .
Physics does not begin to go through biology. Then why should it begin with a discussion of laboratory experiments and their results, which even in the case of simple experiments are the result of many complex and complicated processes?
On the one hand, I can understand why experiment is paramount. We are talking about physics in the end.
On the other hand, giving students a sophisticated mathematical apparatus only so that they can analyze simple experience is already too much . Programmers, for example, are first taught to add two variables, and only then - to write multi-threaded applications; and do not care that the latter are "closer to real life."
Classical mechanics does not follow explicitly from quantum mechanics. Moreover, classical mechanics is at a much higher level. Compare atoms and molecules with quarks: millions of known chemicals, hundreds of chemical elements, and only six quarks. At first it is better to understand the simple, and only then move on to the complex.
Finally , I will consider quantum mechanics from a strictly realistic point of view - our world is a quantum one, our equations describe a territory, not its map, and the world we are familiar with exists implicitly in a quantum world. If there are anti-realists among my readers, pleasekeep your comments. Quantum mechanics is much more difficult to understand and imagine if you doubt its validity. I will talk about this in more detail in one of the following articles.
I think that the majority of theoretical physicists adhere to the point of view that I will present in this introduction. But you should still know that this is not the only possible point of view, and a considerable proportion of scientists doubt the fidelity of a realistic position. Although I am not going to pay attention to any other theories right now , I feel obligated to mention that they are .
To summarize , my goal is to teach you how to think as a native of the quantum world , and not as a tourist unwillingly .
Hold on tight to reality. We begin.
Configurations and Amplitudes
Look at the pic. 1. A half-silvered mirror is located at point A , and two photon detectors at points B and C.

This simple experiment at one time made scientists break their heads. The fact is that in half the cases, a photon emitted towards the mirror was detected by the first detector, and in half by the second. And scientists - attention, get ready to laugh - assumed that the mirror was either passing a photon or reflecting it.
Ha ha ha, imagine a mirror that can choose whether to pass a photon to it or not! If you can imagine it, then don’t do it anyway - otherwise you will get confused just like those scientists. The mirror behaves exactly the same in both cases.
If we tried to write a computer program simulating this experiment (and not just predicting the result), it would look something like this ...
At the beginning of the program, we declare a variable that stores a certain mathematical object - a configuration . It represents a certain description of the state of the world - in this case, “one photon flies to point A”.
In fact, the configuration is described by a complex number (I recall that complex numbers have the form (a + b i ), where a and b are real numbers, and i is an imaginary unit, i.e. such a number that i ² = -1) . Our configuration “photon flies to point A ” also corresponds to some number. Let it be (-1 + 0i ). In what follows, we will call the number corresponding to the configuration its amplitude .
We introduce two more configurations: “photon flies from A to point B ” and “photon flies from A to point C ”. We do not yet know the amplitudes of these configurations; they will be assigned values during program execution.

The amplitudes can be calculated by applying the rule according to which the mirror works to the initial configuration. Without going into details, we can assume that the rule looks like this: “multiply by 1 when the photon flies; multiply by i when the photon is reflected. " We apply the rule: the amplitude of the configuration “photon flies in B ” equals (-1 + 0 i) × i = (0 + - i ), and the amplitude of the configuration “photon flies in C ” is (-1 + 0 i ) × 1 = (-1 + 0 i ). Other configurations in fig. 1 no, so we are done.
In principle, we can consider “the first detector detects a photon” and “the second detector detects a photon” as separate configurations, but this does not change anything; their amplitudes will be equal to the amplitudes of the two previous configurations, respectively. (In fact , they still need to be multiplied by a factor equal to the distance from A to the detectors, but we just assume that all distances in our experiment are unit multipliers.)
So, here is the final state of the program:
- "Flies in the photon A »: (-1 0 + i )
- “Photon flies from A to B ”: (0 + - i )
- "The photon flies from A to C ": (-1 + 0 i )
And, perhaps:
- "The first detector worked": (0 + - i )
- "The second detector worked": (-1 + 0 i )
Of course, no matter how many times we run the program, the final state will remain the same.
Now, for quite complex reasons, which I will not go into yet, there is no easy way to measure the amplitude of the configuration. The state of the program is hidden from us.
What to do?
Although we cannot measure the amplitude directly, we have something - namely, a magical measuring gizmo that can tell us the square of the amplitude module of the configuration. In other words, for the amplitude (a + b i ), the contraption will respond with the number (a² + b²).
It would be more accurate to say that the magic contraption is just an attitudesquares of modules to each other. But even this information is enough to understand what is happening inside the program and by what laws it works.
Using contraption, we can easily find out that the squares of the configuration modules “the first detector worked” and “the second detector worked” are equal. And after conducting some more complex experiments, we can also find out the ratio of the amplitudes themselves - i to 1.
By the way, what kind of magical measuring thing is this?
Well, when such experiments are carried out in real life, the magic thing is that the experiment is carried out a couple of thousand times and just counts how many times the photon was in the first detector, and how many - in the second. The ratio of these values will be the ratio of the squares of the amplitude modules.Why this will be so is another, much more complicated question. In the meantime, you can use the gizmo without understanding how and why it works. Everything has its time.
You may ask: “Why do we need a quantum theory if its predictions coincide with the predictions of the billiard theory?” There are two reasons. First, reality , no matter what you think, still obeys quantum laws - amplitudes, complex numbers and all that. And secondly, the "billiard" theory does not work for any more or less complex experiment. Want an example? You are welcome.
In fig. 2 you can see two mirrors at points B and C , and two half-mirrors at points A and D. Later I will explain why the segment DE is drawn with a dotted line; it will not affect the calculations in any way.

Let's apply the rules that we already know.
In the beginning we have the configuration “photon flies in A ”, its amplitude is (-1 + 0 i ).
We consider the amplitudes of the configurations “photon flies from A to B ” and “photon flies from A to C ”:
- “Photon flies from A to B ” = i × “photon flies to A ” = (0 + - i )
- “Photon flies from A to C ” = 1 × “photon flies to A ” = (-1 + 0 i )
It is intuitively clear that an ordinary mirror behaves like half a half-mirror: it always reflects a photon, it always multiplies the amplitude by i . So:
- “Photon flies from B to D ” = i × “photon flies from A to B ” = (1 + 0 i )
- “Photon flies from C to D ” = i × “photon flies from A to C ” = (0 + - i )
It is important to understand that “from B to D ” and “from C to D ” are two different configurations. You can’t just write “the photon flies to D ”, because what happens to it next depends on the angle at which this photon arrives at D.
We consider further:
- the amplitude of the configuration "photon flies from B to D " equal to (1 + 0 i ):
- multiplied by i , and the result (0 + i ) is counted in favor of the configuration “photon flies from D to E ”
- multiplied by 1, and the result (1 + 0 i ) is counted in favor of the configuration “photon flies from D to F ”
- the amplitude of the configuration "photon flies from C to D " equal to (0 + - i ):
- multiplied by i , and the result (1 + 0 i ) counts in favor of the configuration “photon flies from D to F ”
- multiplied by 1, and the result (0 + - i ) is counted in favor of the configuration “photon flies from D to E ”
Total:
- “A photon flies from D to E ” = (0 + i ) + (0 + - i ) = (0 + 0 i ) = 0
- "The photon flies from D to F " = (1 + 0 i ) + (1 + 0 i ) = (2 + 0 i )
The ratio of the squares of the amplitude modules is 0 to 4; from the calculations it follows that the first detector will not work at all ! Therefore, the segment DE was drawn by the dotted line in Fig. 2.

If half-mirrors reflected or transmitted a photon randomly, both detectors would respond with approximately the same frequency. But this does not coincide with the experimental results. That's all.
You could argue: “And that’s not all! Suppose, for example, that when a mirror reflects a photon, something happens to it that it will not be reflected a second time? And, conversely, when a mirror passes a photon, it will have to reflect next time. ”
First, Occam’s razor. Do not come up with a complicated explanation if a simple one already exists (if, of course, quantum mechanics is consideredsimple ...) And secondly, I can come up with another experience that will refute this alternative theory.
We place a small opaque object between B and D so that the amplitude of the configuration “photon flies from B to D ” is always zero.

Now the amplitude of the configuration “photon flies from D to F ” is (1 + 0 i ), and the amplitude of the configuration “photon flies from D to E ” is (0 + - i ). The squares of the modules are 1. This means that in half the cases the first detector will fire, and in half the second.
It's impossibleexplain if we assume that the photon is a small billiard ball that is reflected from the mirrors.
The fact is that one cannot think of amplitude as probability. In probability theory, if event X may or may not occur, then the probability of event Z is P ( Z | X ) P ( X ) + P ( Z | ¬ X ) P (¬ X ), where all probabilities are positive. If you know that the probability Z provided that X happened is 0.5 and the probability X is 0.3, then the total probability Z is at least 0.15, regardlessfrom what will happen if X does not happen. There are no negative probabilities. Possible and impossible events cannot annul each other. And amplitudes can.

Here is an example of wrong thinking: “A photon flies to B or C , but it could fly differently, and this affects the likelihood that it will fly to E ...”
Events that did not happen have no effect on the world. The only thing that can affect the world is our imagination. “Oh my God, this car almost knocked me down,” you think, and decide to leave for the monastery so that you will never meet dangerous cars again. But really still notthe event itself , but only your imagination, contained in your brain - which you can get out, feel and put back from you to make sure that it is real.
Really everything that affects the world. (If you think this is not the case, try defining the word “real.”) The configurations and amplitudes directly affect the world, so they are also real. To say that a configuration is “something that could happen” is as strange as saying that a chair is “something that could happen”.
And what then is the configuration?
To be continued.
In fact, everything is a little more complicated than you might think after reading this article.
Each configuration describes all the particles in the universe. Amplitude is a continuous distribution over the entire space of configurations, and not discrete, as we considered today. And in fact, photons are not teleported from one place to another instantly , and each different state of the world is described by a new configuration. In the end, we get to that.
If you do not understand anything from this paragraph, do not worry, I will explain everything. Later.
read part two →
Posted by Eliezer Yudkowsky. Free and shortened (quite a bit) translation: I. Links to the originals: , .
lesswrong.com/lw/pc/quantum_explanationslesswrong.com/lw/pd/configurations_and_amplitude