How to count google.com page hits? And how to store the counter of likes of very popular users? This article proposes to consider the solution of these problems using CRDT (Conflict-free Replicated Data Types, which in Russian translates roughly as Conflict-Free Replicated Data Types), and in the more general case - replica synchronization tasks in a distributed system with several leading nodes.

1. Introduction

We have long been accustomed to using applications such as a calendar or a note service such as Evernote. They are united by the fact that they allow you to work offline, from multiple devices and to several people at the same time (on the same data). The challenge facing the developers of each such application is how to ensure the most “smooth” synchronization of data changed simultaneously on several devices. Ideally, user involvement should not be required at all to resolve merge conflicts.

In a previous article, we already considered an approach to solving such problems - Operational Transformation, it will also describe a very similar method that has both advantages and disadvantages (for example, CRDT for JSON has not yet been invented. Upd: Thanks to msvnfor the link, here is the project from the authors of a research article on the implementation of JSON in CRDT)

2. Strong eventual consistency

Recently, a lot of work has been written and a lot of research has been done in the field of eventual consistency. In my opinion, now there is a strong trend towards a shift from strong consistency to various options for consistency, to research which consistency in which situations / systems is more profitable to apply, to rethinking existing definitions. This leads to some confusion, for example, when the authors of some works, talking about consistency, mean eventual consistency with some additional property, and other authors use certain terminology for this.

The question raised by the authors of one of the articles criticizes the current definition of eventual consistency: according to it, if your system always answers “42” to all requests, then everything is OK, it is eventually consistent.

Without violating the correctness of this article, I, following the authors of the original articles, will use the following terminology (please note, these are not strict definitions, these are differences):

• Strong consistency (SC): all write operations are strictly ordered, a read request on any replica returns the same, last recorded result. Real-time consensus is needed to resolve conflicts (with the ensuing consequences), can withstand a drop to n / 2 - 1 nodes.
• Eventual consistency (EC): we update the data locally, we send the update further. Reading on different replicas can return stale data. In case of conflict, we either roll back, or somehow decide what to do. T.O. consensus is still needed, but not in real time .
• Strong eventual consistency (SEC): EC + has a predefined algorithm for resolving conflicts. T.O. consensus is not needed ; it can withstand a drop to n - 1 nodes.

Note that SEC (as it were) solves the problem of the CAP theorem: all three properties are satisfied.

So, we are ready to donate SC and want to have some set of basic data types for our potentially unstable distributed system, which will automatically resolve write conflicts for us (no user interaction or request to some arbiter is required)

3. Tasks about likes and hits

Undoubtedly, there are several algorithms for solving such problems. CRDT offers a fairly elegant and easy way.

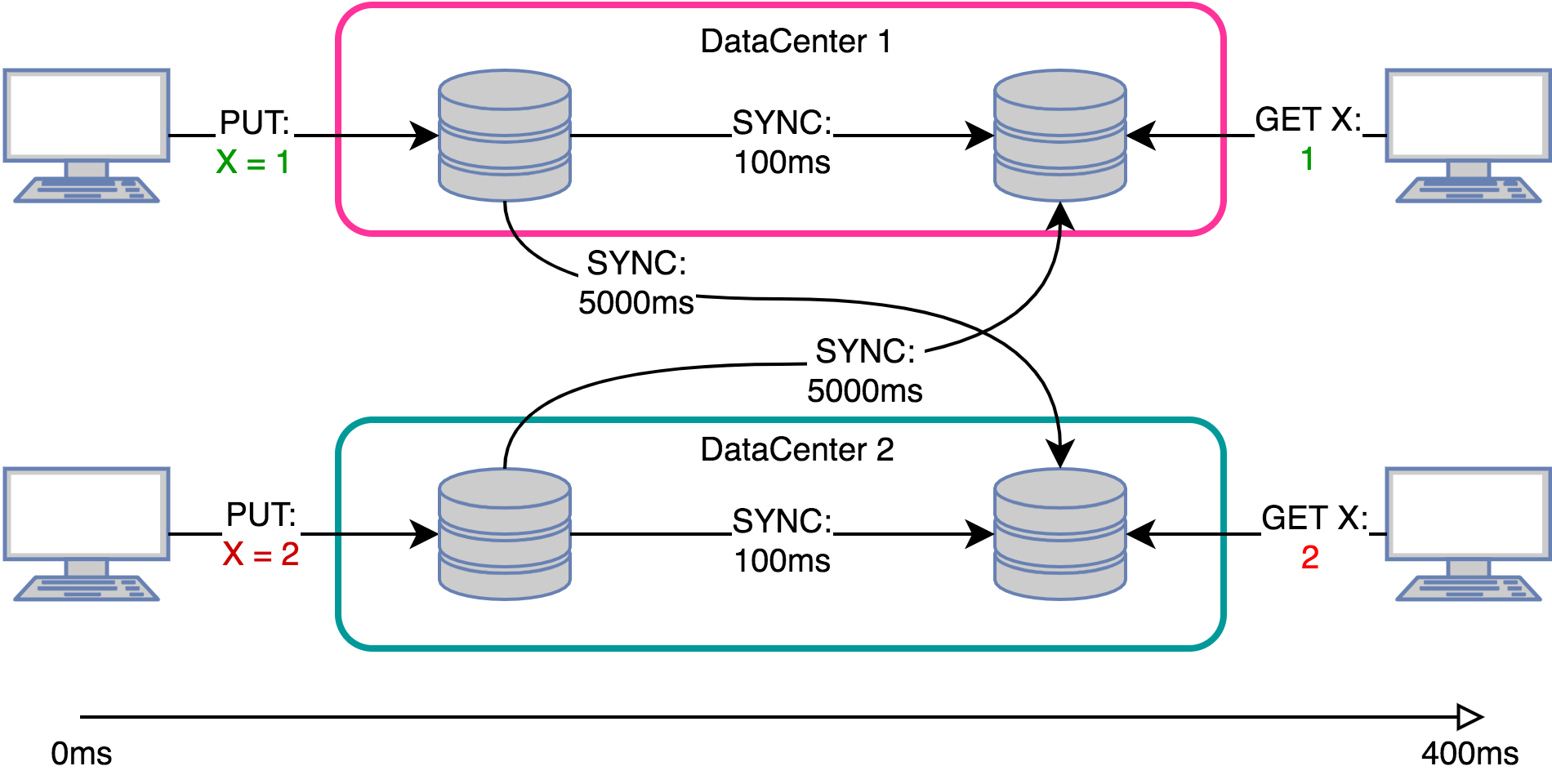
Google.com hit count:

google.com processes approximately 150,000 requests per second from all over the world. Obviously, the counter needs to be updated asynchronously. Queues partially solve the problem - for example, if we provide an external API to get this value, then we will have to do replication so as not to put the repository with read requests. And if there is already replication, maybe without global queues?

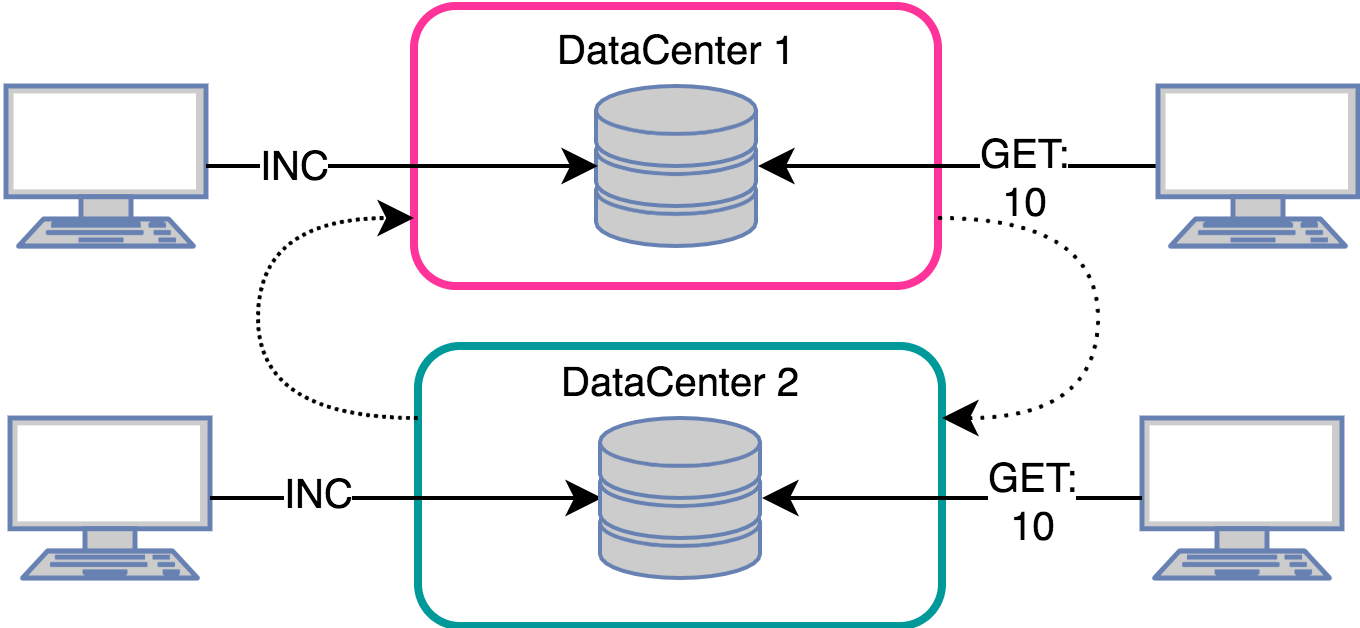
Counting user likes:

The task is very similar to the previous one, only now you need to count unique hits.

4. Terminology

For a more complete understanding of the article, you need to know about the following terms:

1. Idempotency It
   says that applying the operation several times does not change the result.
   Examples - GET operation or addition with zero:$$
   
2. Commutativity
   $$
   
3. Partial order
   Reflexivity + Transitivity + Antisymmetry
   
4. Semilattice
   Partially ordered set with exact upper (lower) face
   
5. Vector of Versions
   A vector of dimension equal to the number of nodes, and each node, when a certain event occurs, increments its value in the vector. During synchronization, data is transmitted with this vector and this introduces an order relation, which allows you to determine which replica has old / new data.

5. Sync models

State-based:

Also called passive synchronization, it forms the Convergent Replicated Data Type - CvRDT.
Used in file systems such as NFS, AFS, Coda, and in KV repositories Riak, Dynamo.
In this case, the replicas exchange states directly, the receiving replica merges the received state with its current state.


To perform convergence of replicas using this synchronization, it is necessary that:

• The data formed a semilattice
• The merge function produced an exact upper bound
• The replicas formed a connected graph.

Example:

• Dataset: natural numbers $$
• Minimum item: $$
• $$

Such requirements give us a commutative and idempotent merge function that grows monotonically on a given data set:


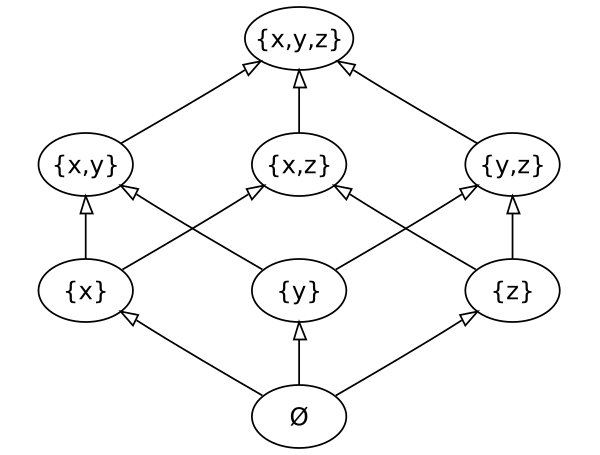
This ensures that the replicas converge sooner or later and allows you not to worry about the data transfer protocol - we can lose messages with a new state, send them several times, and even send them in any order .

Operation-based:

Also called Active Synchronization, it forms the Commutative Replicated Data Type - CmRDT.
Used in cooperative systems such as Bayou, Rover, IceCube, Telex.

In this case, the replicas exchange state update operations. When updating data, the original replica:

• Calls the generate () method, which returns the effector () method to execute on the remaining replicas. In other words, effector () is the closure for changing the state of the remaining replicas.
• Applying an effector to a local state
• Sends effector to all other replicas

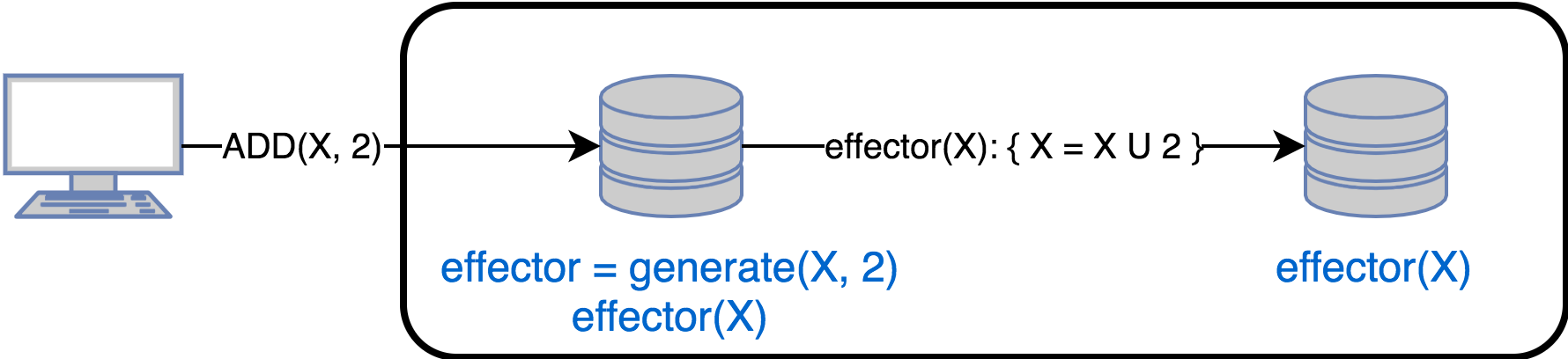
To perform convergence of replicas, the following conditions must be met:

• Reliable Delivery Protocol
• If effector is delivered to all replicas in accordance with the entered order (for a given type), then simultaneous effectors are commutative, or
• If effector is delivered to all replicas without taking into account the order, then all effector are commutative.
• In case the effector can be delivered several times, then it must be idempotent
• Some implementations use queues (Kafka) as part of the delivery protocol.

Delta-based:

Considering state / op based it is easy to notice that if an update changes only part of the state, then it makes no sense to send the entire state, and if a large number of changes affect one state (for example, a counter), then you can send one, aggregated change, and not all operations changes.

Delta synchronization combines both approaches and sends out delta-mutators that update the state according to the latest synchronization date. At the initial synchronization, it is necessary to send the state completely, and some implementations in such cases already take into account the state of the remaining replicas when constructing delta-mutators.

The next optimization method is to compress the op-based log if delays are allowed.

Pure operation-based:

There is a delay in creating opector based op-based synchronization. In some systems this may not be acceptable, then you have to send out the original change at the cost of complicating the protocol and the additional amount of metadata.

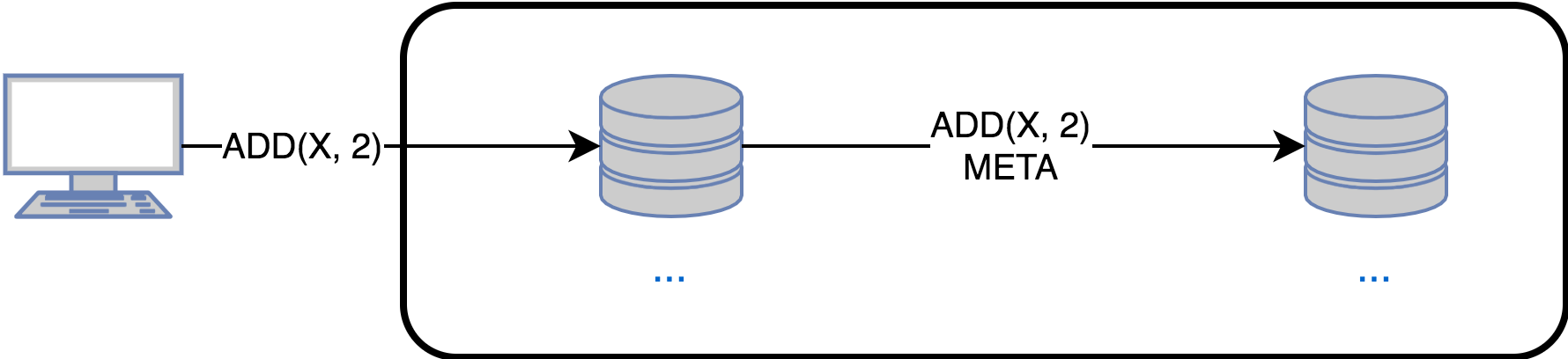
Standard use approaches:

• If updates are to be sent out immediately in the system , then state-based would be a bad choice, since sending out the whole state is more expensive than just an update operation. Delta-based works better, but in this particular case the difference with state-based will be small.
• If you need to synchronize the replica after a failure , then state-based and delta-based are the perfect choice. If you have to use op-based, then the possible options are:
  
  1) Roll all the missed operations from the moment of failure
  2) A full copy of one of the replicas and roll of the missed operations
• As noted above, op-based requires that updates be delivered exactly once to each replica. The delivery requirement only once can be omitted if the effector is idempotent. In practice, it is much easier to implement the first than the second.

The relationship between Op-based and State-based:

Two approaches can be emulated through each other, so that in the future we will consider CRDT without reference to any specific synchronization model.

6. CRDT

6.1 Counter

An integer that supports two operations: inc and dec. As an example, consider possible implementations for op-based and state-based synchronizations:

Op-based counter:

Obviously enough, just sending updates. Example for inc:

function generator() { return function (counter) { counter += 1 } }

State-based counter:

The implementation is no longer so obvious, since it is unclear what the merge function should look like.

Consider the following options:

Monotonically increasing counter (Increment only counter, G-Counter):

Data will be stored as a vector of dimension equal to the number of nodes (version vector) and each replica will increase the value in the position with its id.

The merge function will take a maximum in the corresponding positions, and the final value is the sum of all elements of the vector

$$

You can also use the G-Set (see below).

Application:

• Counting clicks / hits (sic!)

Counter-enabled decrement (PN-counter)

Set up two G-counter - one for the increment operation, the second - to decrement

Application:

• The number of logged-in users in a p2p network, such as Skype

Non-negative counter

A simple implementation does not yet exist. Suggest your ideas in the comments, discuss.

6.2 Register

A memory cell with two operations - assign (write) and value (read).
The problem is that assign is not commutative. There are two approaches to solve this problem:

Last-Write-Wins Register (LWW-Register):

We enter the full order through the generation of unique id for each operation (timestamp, for example).

An example of synchronization is the exchange of pairs (value, id):


Application:

• Columns in cassandra
• NFS - file in whole or in part

Multi-Value Register (MV-Register):

The approach is similar to a G-counter - we store the set (value, version vector). Register value - all values, when merged - LWW separately for each value in the vector.


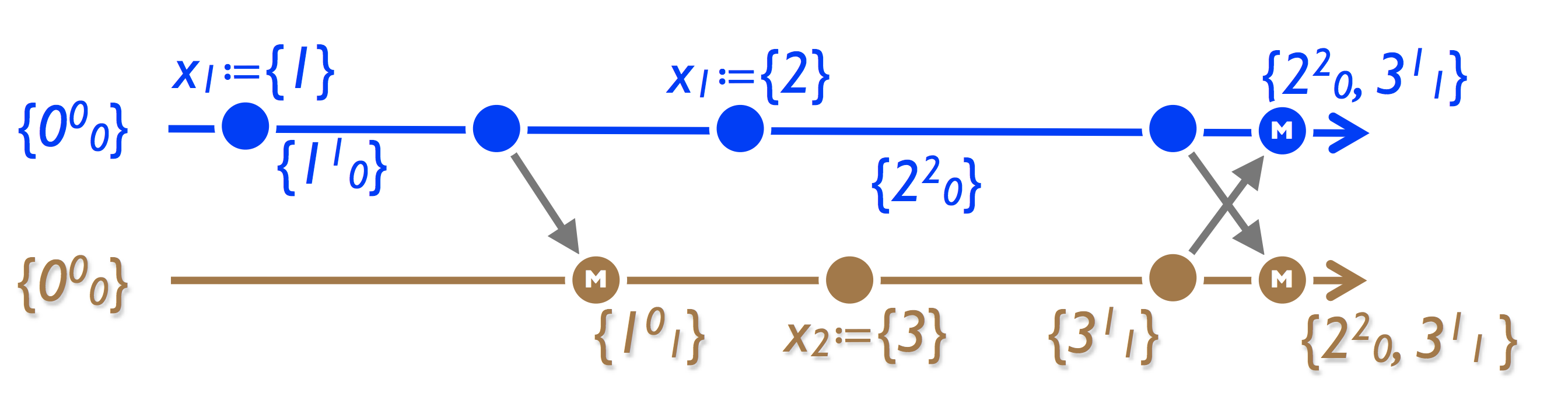
Application:

• Basket in Amazon. A well-known bug is associated with this, when after removing an item from the basket it appears there again. The reason is that despite the fact that the register stores a set of values, it is not a set (see the picture below). Amazon, by the way, does not even consider this a bug - in fact, it increases sales.
• Riak. In a more general case, we shift the problem of choosing the actual (note - there is no conflict!) Value to the application.

Explanation of a bug in Amazon:

6.3 Lots

The set is the basic type for building containers, mappings, and graphs and supports operations - add and rmv, which are not commutative.

Consider a naive implementation of an op-based set, in which add and rmv are executed as they arrive (add comes to replica 1 and 2, then rmv goes to 1)


As you can see, the replicas eventually dispersed. Consider the various options for constructing conflict-free sets:

Growing Set (G-Set):

The simplest solution is to prevent items from being deleted. All that remains is the add operation, which is commutative. The merge function is the union of sets.

Two Phase Set (2P-Set):

We allow you to delete, but you cannot add it again after removal. To implement, we create a separate set of remote G-set elements (such a set is called a tombstone set)
Example for state-based:

$$

LWW-element Set:

The next way to implement a conflict-free set is to introduce a complete order, one option is to generate unique timestamps for each element.

We get two sets - add-set and remove-set, when add () is called, add (element, unique_id ()), when checking if there is an element in the set - look where timestamp is greater - in remove-set or in add-set

PN-Set:

Variation with ordering of the set - we start a counter for each element, when we add it, we increase it, when we delete it we decrease it. An element is in the set if its counter is positive.

Note the interesting effect - in the third replica, adding an element does not lead to its appearance.

Observe-Remove Set, OR-Set, Add-Win Set:

In this type, add takes precedence over remove. Implementation example: we assign a unique tag to each newly added element (relative to the element, and not to the entire set). Rmv removes an element from the set and sends all the seen pairs (element, tag) to the replicas for removal.

Remove-win Set:

Similar to the previous one, but at the same time add / rmv rmv wins.

6.4 Graph

This type is built on the basis of many. The problem is this: if there are simultaneous operations addEdge (u, v) and removeVertex (u) - what should I do? The following options are possible:

• RemoveVertex priority, all edges incident to this vertex are deleted
• AddEdge priority, deleted vertices restored
• We delay the execution of removeVertex until all simultaneous addEdge are executed.

The easiest option is the first, for its implementation (2P2P-Graph) it is enough to get two 2P-Set, one for the vertices, the second for the edges

6.5 Display

Map of literals:

Two problems to solve:

• What to do with simultaneous put operations? By analogy with counters, you can choose either LWW or MV semantics
• What to do with simultaneous put / rmv? By analogy with sets, you can either put-wins, or rmv-wins, or last-put-wins semantics.

CRDT mapping (Map of CRDTs):

A more interesting case, because allows you to build nested mappings. We do not consider cases of changing nested types - this should be decided by the nested CRDT itself.

Remove-as-recursive-reset map

The remove operation “resets” the type value to some starting state. For example, for a counter, this is a zero value.

Consider an example - a general shopping list. One of the users adds flour, and the second one checks out (this leads to a call to the delete operation on all elements). As a result, one unit of flour remains on the list, which seems logical.


Remove-wins map

The rmv operation takes precedence.

Example: in an online game, an Alice player has 10 coins and a hammer. Then two events simultaneously occur: on replica A, she produced a nail, and on replica B, her character is deleted with the removal of all objects:



Note that when using remove-as-recursive, a nail would eventually remain, which is not the correct state when the character is removed.

Update-wins map

Updates take precedence, or rather, cancel previous operations to delete simultaneous rmv.

Example: in an online game, the Alice character on replica B is deleted due to inactivity, but activity occurs on replica A at the same time. Obviously, the delete operation must be canceled.


There is one interesting effect when working with such an implementation - suppose that we have two replicas, A and B, and they store the set by some key k. Then, if A deletes the value of the key k, and B deletes all the elements of the set, then in the end the replicas will leave an empty set with the key k.

Note that a naive implementation will not work correctly - you cannot simply undo all previous delete operations. In the following example, with this approach, the final state would be as the initial state, which is incorrect:

List

The problem with this type is that element indices on different replicas will be different after local insert / delete operations. To solve this problem, the Operational Transformation approach is applied - when applying the obtained change, the index of the element in the original replica should be taken into account.

7. Riak

As an example, consider CRDT in Riak:

• Counter: PN-Counter
• Set: OR-Set
• Map: Update-wins Map of CRDTs
• (Boolean) Flag: OR-Set where maximum 1 element
• Register: pairs (value, timestamp)

8. Who uses CRDT

The wiki section contains good examples.

9. References

• Key-CRDT Stores
• A Conflict-Free Replicated JSON Datatype
• A comprehensive study of Convergent and Commutative Replicated Data Types
• Convergent and Commutative Replicated Data Type
• Conflict-free replicated data type
• A Bluffers Guide to CRDTs in Riak
• CRDTs: An UPDATE (or just a PUT)
• Conflict-free Replicated Data Types: An Overview
• Strong Eventual Consistency and Conflict-free Replicated Data Types
• Eventually-Consistent Data Structures