Surprise: the Hubble constant is actually fickle

Part of the image obtained in the framework of the observation of the Hubble eXtreme Deep Field , in the combined ultraviolet, visible light and infrared radiation - the deepest look into the Universe from all that we have taken. The different galaxies visible here are at different distances and have a different redshift, which allows us to derive the Hubble law.

The universe is huge, and for billions of light years in all directions filled with stars and galaxies. From the Big Bang itself, the light travels, going from each source that created it, and a very small part of this light reaches our eyes. But light does not simply move through space from the point of emission to the place where we are today; besides this, the fabric of space itself expands.

The farther away the galaxy is from us, the more the space between us stretches — and shifts to the red part of the spectrum — the light that eventually comes to our eyes. Looking at increasingly distant distances, we see an increase in redshift. If we plot how the apparent removal rate depends on distance, we get a beautiful, straightforward relationship: the Hubble law . But the slope of this line, the Hubble constant, is actually not at all constant. And this is one of the strongest misconceptions in all astronomy.


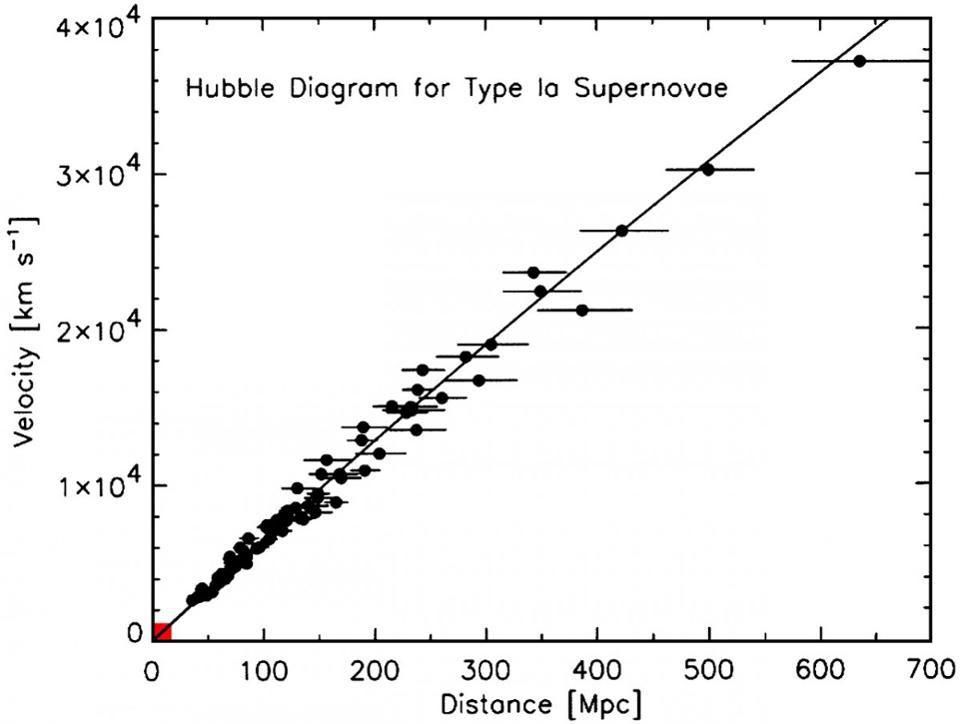
Dependence of redshift on distance for distant galaxies. The points not falling on the line are shifted due to the difference in peculiar velocities , but they only deviate slightly from the observed overall picture. The initial data, obtained by Edwin Hubble himself, and first used to demonstrate the expansion of the Universe, fit into a small red rectangle in the lower left corner.

We understand the expansion of the universe in two ways: theoretically and through observation. Observing the Universe, we see several important facts related to expansion:

• The universe expands at the same speed in all directions.
• The farther the galaxy is, the faster it is moving away from us.
• All this is true only on average.

In individual galaxies, there is a large scatter of real velocities, existing due to gravitational interactions with all the substance of the Universe.


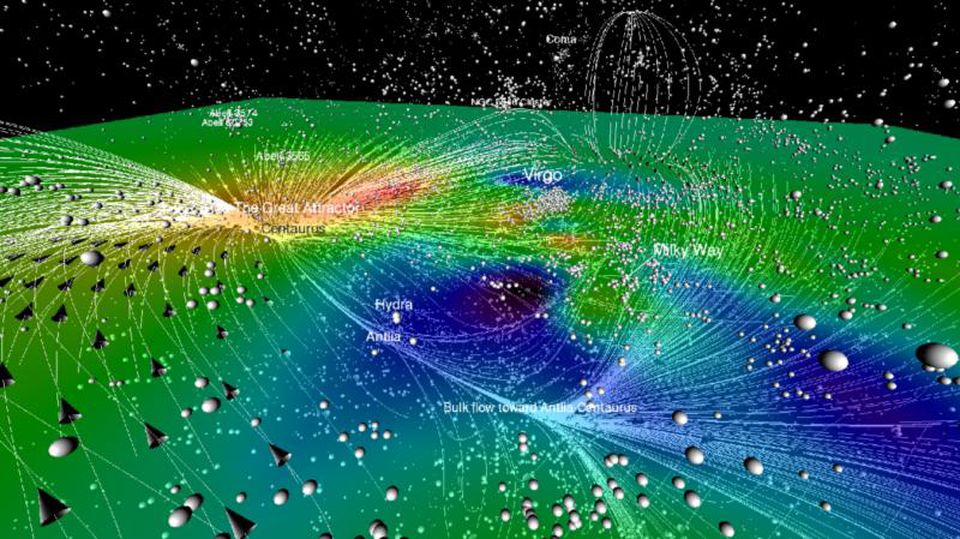
Two-dimensional section of the nearest to us parts of the Universe, whose density is higher (red) and lower (blue / black) of the average value. Lines and arrows show the directions of peculiar velocities, but the whole picture is included in the fabric of the expanding space.

But this problem is not insurmountable. In the universe there are not just several galaxies, the distance and redshift of which we can measure; we carried out such measurements literally for millions of galaxies. We can group a huge number of galaxies so that each group is at a certain average distance from us, and we could calculate their average redshift. After this procedure, we find a straight-line relationship that defines the Hubble law.

But here, what's the surprise. If you look at a sufficiently large distance, it becomes clear that the rate of expansion is no longer subject to the rectilinear law, and begins to round out.


The dependence of the speed of visible expansion (y-axis) on distance (x-axis) corresponds to the fact that the Universe in the past has expanded more rapidly, but it is also expanding today. This is the modern (2014) version of Hubble’s work, extending over distances thousands of times larger. Note that the points do not form a straight line, which means that the rate of expansion varies with time.

Using the term "Hubble constant", we mean the slope of this line. If this is not a line - that is, if its slope changes - this suggests that the Hubble expansion rate of the Universe is not a constant! We call it the Hubble constant because the Universe expands at the same speed at any point: the Hubble constant is constant in space.

But the rate of expansion, and the value of the Hubble constant, change over time. This is not a mystery, but something to be expected. To understand this, let's look at it from a different point of view: theoretical.


Ethan Siegel on the background of the hyperstyle of the American Astronomical Society in 2017, together with the first Friedmann equation, on the right.
# My Favorite Equation
The first Friedmann equation predicts the rate of expansion of the Universe based on its contents

The first Friedman equationit turns out with us, if we start with the Universe, uniformly filled with matter, radiation and all other forms of energy. The only assumptions used here are that the Universe is isotropic (the same in all directions), homogeneous (it has the same density everywhere) and obeys the General Theory of Relativity. By accepting this, you get the relationship of the magnitude of H, the Hubble velocity (left), and various forms of matter and energy of the Universe (right):


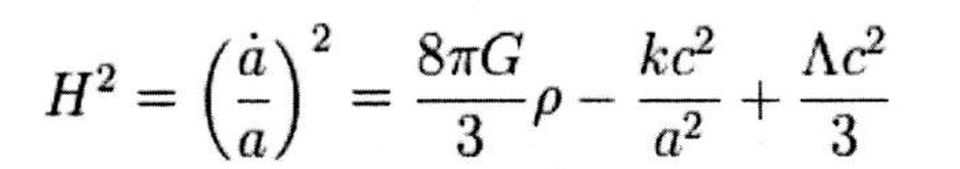
The first Friedmann equation, as it is usually written today. The left part determines the expansion rate and the evolution of space-time, and the right includes all the various forms of matter and energy, as well as spatial curvature

Interestingly, with the expansion of the Universe, the density of matter, radiation and energy can vary. For example, with the expansion of the Universe its volume increases, but the total number of particles remains unchanged. This means that in an expanding universe:

• matter density drops as a ^-3 ,
• radiation density falls as a ^-4 ,
• dark energy density remains constant, and evolves as a ⁰ ,

where a is the scale factor (distance or radius) of the Universe. Over time, a grows, and the various components of the universe become more or less important relative to each other.


As matter (above), radiation (in the middle) and the cosmological constant (below) develop over time in an expanding universe, the

Universe with a higher energy density expands faster. Conversely, a universe with a lower energy density expands more slowly. With age, the Universe expands: when expanding, matter and radiation become less dense; with decreasing density decreases the rate of expansion. At any time, the rate of expansion determines the value of the Hubble constant. In the distant past, the expansion rate was much higher, and today it is the lowest.


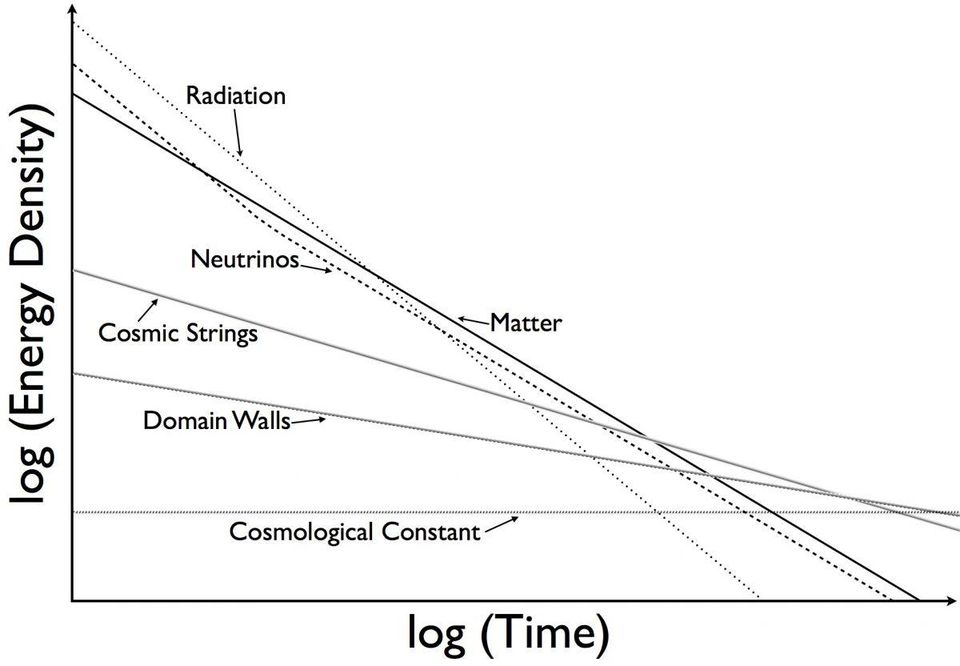
Various components and contributions to the energy density of the Universe, and periods of their dominance. If cosmic strings or domain walls existed in any significant amount, they would make a significant contribution to the expansion of the Universe. There may even be some other components of the Universe that we no longer see, or who are still going to prove themselves! By now, dark energy dominates, matter is important enough, and radiation can be neglected.

So why do very distant galaxies obey this straightforward relationship? Because all the light that comes to our eyes, from the light emitted by a neighboring galaxy, to the light emitted by a galaxy located in billions of light years from us, reaches the age of 13.8 billion years by the time we approach us. By the time the light arrived, everything in the Universe had lived in the same constantly changing Universe as we. Hubble's constant in the past, when most of the world was emitted, was higher, but it took billions of years for this light to come to our eyes.


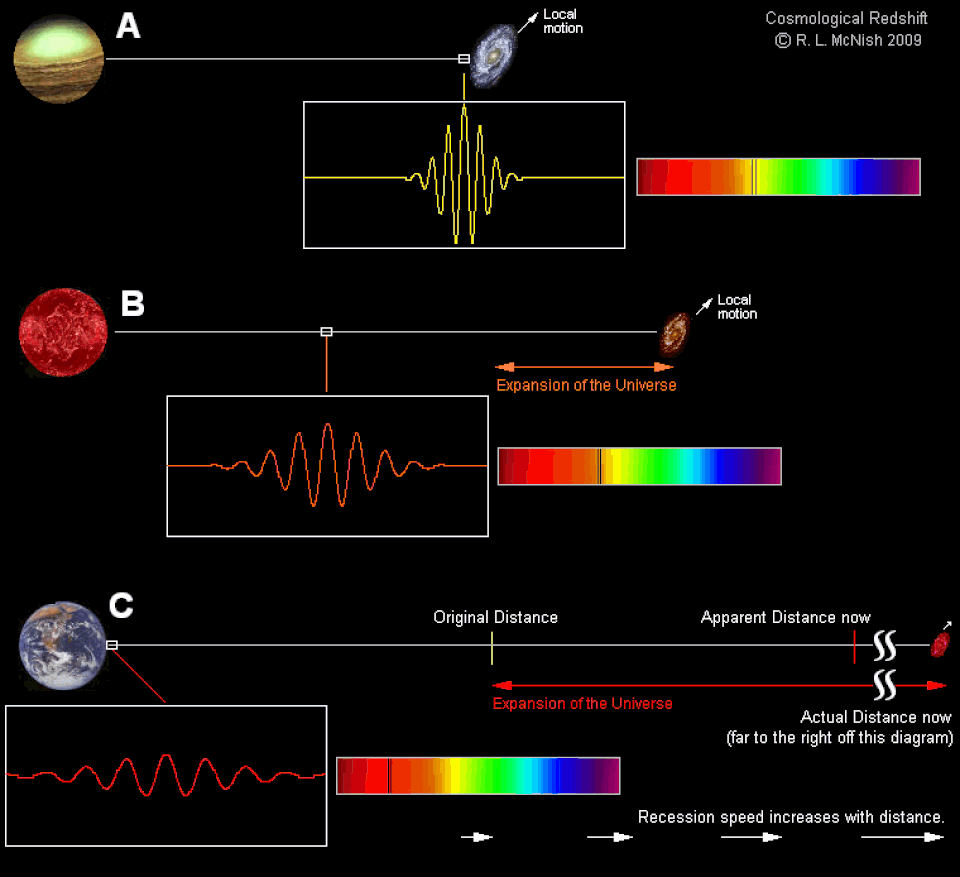
Light can be emitted with a different wavelength, but the expansion of the universe will stretch it along the way. Light emitted by a galaxy 13.4 billion years ago in the ultraviolet will be shifted to the infrared range.

Over time, the universe expanded, which means that the wavelength of light increased. Dark energy has become quite important only in the last 6 billion years, and we have reached the point where it quickly becomes the only component of the Universe, affecting the rate of its expansion. If we returned at a time when the universe was two times younger, then the expansion rate would be 80% more than today. And when the universe was 10% of the current age, the expansion rate was 17 times greater than today.

When the universe is ten times older than today, its expansion rate will be 18% of today's.


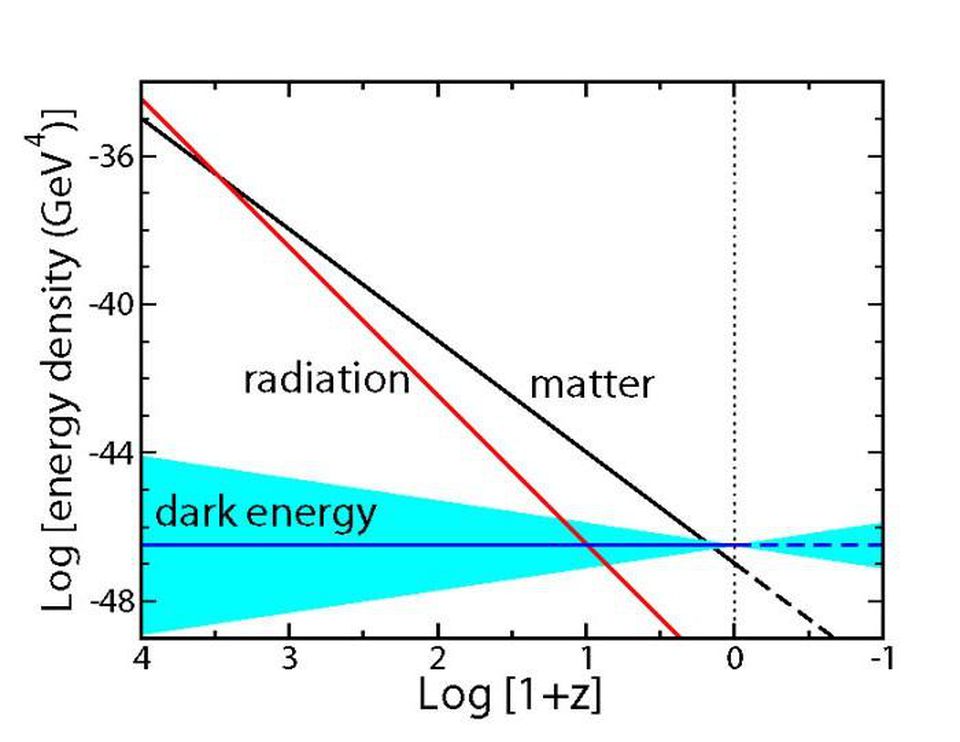
Blue overshadows the range of possible uncertainties of how dark energy density may deviate in the past and future. The data indicate the presence of a true cosmological "constant", but no one has yet rejected any other possibilities. Unfortunately, the transformation of matter into radiation cannot be a candidate for dark energy; as a result of it, what used to behave like matter just behaves like radiation.

All because of the presence of dark energy, which behaves like a cosmological constant. In the distant future, matter and radiation will become relatively unimportant compared to dark energy, which means that the energy density of the Universe will remain constant. In such conditions, the expansion rate will reach a stable and finite value, and this will remain so. In the distant future, the Hubble constant will become constant not only in space, but also in time.

In the distant future, by measuring the speed and distance to all visible objects, we get the same slope of this line everywhere. Hubble's constant will become truly constant.


The relative importance of the various components of the energy of the universe at different times in the past. When the dark energy approaches 100% in the future, the energy density of the Universe will remain constant for an arbitrarily long period of time.

If astronomers were more precise in their words, they would call H the Hubble parameter, and not the Hubble constant, because it changes with time. But for several generations we could measure relatively small distances, and H seemed to be constant, so we did not rename it. We only have to clarify that H is a function of time, and only today - when we call it H ₀- it is constant. In fact, the Hubble parameter varies with time, and remains constant only throughout the entire space. But if we lived to a distant future, we would see that H at some point ceases to change. Today we can carefully separate real constant values ​​and those that change over time, but in the distant future, due to the dark energy, this difference will not be.