Solving color Japanese crosswords at the speed of light

Japanese crosswords (also nonograms) are logical puzzles in which a pixel image is encrypted. Solve crossword need with the help of numbers located to the left of the rows and above the columns.

The size of the crossword puzzles can be up to 150x150. The player with the help of special logical techniques calculates the color of each cell. The solution can take as little as a couple of minutes on beginner crossword puzzles, as well as dozens of hours on complex puzzles.

A good algorithm can solve the problem much faster. The text describes how using the most appropriate algorithms (which generally lead to a solution), as well as their optimizations and using C ++ features (which reduce the operating time by several dozen times) to write a solution that works almost instantly.

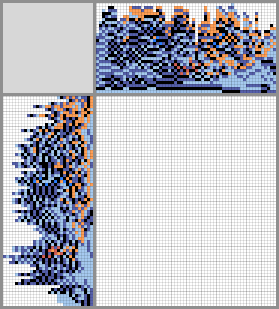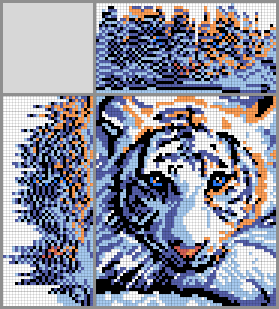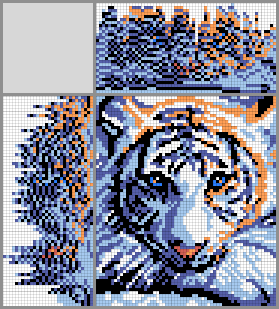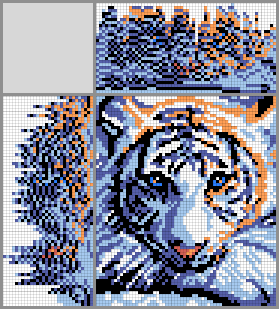
In the mobile version of Habr, formulas in the text may not be shown (not in all mobile browsers) - use the full version or another mobile browser if you notice problems with formulas

Rules of the game

Initially, the crossword canvas is white. For vanilla black and white crosswords, you need to restore the location of black cells.

In black-and-white crossword puzzles, the number of numbers for each row (to the left of the canvas) or for each column (above the canvas) indicates how many groups of black cells are in the corresponding row or column, and the numbers themselves - how many fused cells each of these groups contains. Set of numbers$$ means that in a certain row there are three consecutive groups of $$, $$ and $$black cells in a row. Groups can be arranged in a row as horrible, without disturbing the relative order (numbers specify their length, and the position must be guessed), but they must be separated by at least one white cell.

Correct example

In color crosswords, each group still has its own color - any, except white, is a background color. Neighboring groups of different colors can stand close together, but for neighboring groups of the same colors, the separation of at least one white cell is necessary.

What is not a Japanese crossword puzzle

Each pixel image can be encrypted in the form of a crossword puzzle. But it may not be possible to recover it back - the resulting puzzle can either have more than one solution, or have one solution, but cannot be solved in a logical way. Then the remaining cells in the process of the game have to guess the shaman technology using quantum computers .

Such crossword puzzles are not grafomania, but graphomania. It is believed that the correct crossword is such that in a logical way you can come to a single solution.

The "logical path" is the ability to restore each cell one by one, considering the row / column separately, or their intersection. If there is no such possibility, the number of considered answers can be very much, much more than a person can count.

Incorrect nonogram is the only solution, but it’s impossible to solve it normally. Orange marked "unsolvable" cells. Taken from Wikipedia.

This limitation is explained in the following way: in the most general case, the Japanese crossword puzzle is an NP-complete problem. However, guessing does not become an NP-complete task, if there is an algorithm, at each instant of time it is unambiguously indicating which cells to open further. All crossword puzzles used by humans (except for the method ofMonte Carlo trial and error), based precisely on this.

In the most Orthodox crossword puzzles, the width and height are divided by 5, there are no rows that can be counted instantly (such as where either the colored cells fill in all the places or they are not at all), and the number of additional colors is limited. These requirements are not mandatory.

Simple simple crossword puzzle:

  |1 1|
--+---+
 1|   |
 1|   |
--+---+

Often, coded pixel art that uses "chess order" to simulate a gradient is not solved. It will be better to understand if you type in the search for "pixelart gradient". The gradient is just like this 2x2 file crossword puzzle.

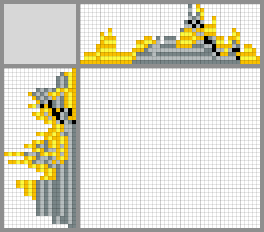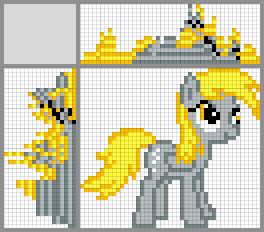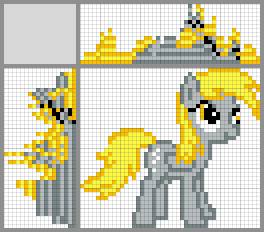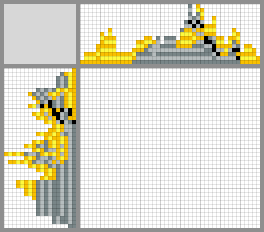
Possible solutions

We have the size of the crossword puzzle, a description of the colors and all the rows and columns. How can you collect from this picture:

Brute force

For each cell, we iterate over all possible states and check for satisfactory. The complexity of this solution for black and white crossword$$for color $$. By analogy with clown sorting, this solution can also be called clown. It is suitable for size 5x5.

Backtracking

All possible methods of arranging horizontal groups of cells are sorted out. We put a group of cells in a row, check that it does not break the description of groups of columns. If it breaks - we put further on 1 cell, we check again. Set - go to the next group. If the group cannot be put in any way - we roll back the two groups, rearrange the previous group, and so on, until we deliver the last group successfully.

Separately for each row

This solution is much better and truly true. We can analyze each row and each column separately. Each row will try to reveal the maximum information.

The algorithm for each cell in the row learns more information - it may turn out that it is impossible to paint the cell in some color, the groups will not converge. The row cannot be fully opened at once, but the information obtained “will help” several columns to open up better, and when we begin to analyze them, they will again “help” the rows, and this will take several iterations until all the cells have one possible color.

Truly the right decision

One line, two colors

Effective guessing of a black-and-white one-line player, for which some cells have already been guessed, is a very tough task. She met in places like:

• The quarter-final of ACM ICPC 2006 - you can try to solve the problem yourself . The time limit is 1 second, the number of groups is limited to 400, the row length is also 400. It has a very high level of complexity compared to other tasks.
• International Olympiad in Informatics 2016 - condition , pass the task . Time limit 2 seconds, limiting the number of groups to 100, the length of the row 200'000. Such constraints are overkills, but solving the problem with ACM constraints is 80/100 points in this task. Here, too, the level did not disappoint, schoolchildren from around the world with a cruel level of IQ are trained for several years to solve different tin, then go to this Olympiad (only 4 people from the country have to go), decide 2 rounds of 5 hoursand in the case of epic win (bronze in different years for 138-240 points out of 600) enrollment at Oxford, then offers from clear companies to the search department, a long and happy life embracing with dakimama.

Monochrome one-liner can also be solved in different ways, and for $$ (enumeration of all variants, check for correctness, selection of cells that have the same color in all variants), and somehow less stupid.

The main idea is to use an analog backtracking, but without unnecessary calculations. If we have somehow put several groups and are now in a certain cell, then it is required to find out whether it is possible to put the remaining groups, starting with the current cell.

defEpicWin(group, cell):if cell >= last_cell: # Условие выигрыша                                       return group == group_size                                              
    win = False# Можем ли вставить группу в этой позиции                                   if group < group_size  # Группы еще есть                                    and CanInsertBlack(cell, len[group])  # Вставка черной группы       and CanInsertWhite(cell + len[group], 1)  # Вставка белой клетки    and EpicWin(group + 1, cell + len[group] + 1):  # Можно заполнить далее
        win = True                                                              
        can_place_black[cell .. (cell + len[group] - 1)] = True                 
        can_place_white[cell + len[group]] = True;                              
    # Можем ли вставить белую клетку в этой позиции                                if CanInsertWhite(cell, 1)                                                     
            and EpicWin(group, cell + 1):                                          
        win = True                                                                 
        can_place_white[cell] = Truereturn win
EpicWin(0, 0)        

This approach is called dynamic programming . The pseudocode is simplified, and there even the memorization of the calculated values ​​is not performed.

Functions CanInsertBlack/CanInsertWhiteare needed to check whether it is theoretically possible to put a group of the desired size in the right place. All they have to do is to check that there is no “100% white” cell in the specified cell range (for the first function) or “100% black” (for the second). So they can work for$$This can be done using partial sums:

white_counter = [ 0, 0, ..., 0 ]  # Массив длины n                              defPrecalcWhite():for i in range(0, (n-1)):                                                        
        if is_anyway_white[i]:  # 1, если i-ая клетка 100% белая                
            white_counter[i]++                                                  
        if i > 0:                                                               
            white_counter[i] += white_counter[i - 1]                            
defCanInsertBlack(cell, len):# Опускаем проверку корректности границ [cell, cell + len - 1]              
    ans = white_counter[cell + len - 1]                                         
    if cell > 0:                                                                
        ans -= white_counter[cell - 1]                                          
    # В ans - количество белых клеток от cell до (cell + len - 1)               return ans == 0

The same witchcraft with partial sums is waiting for a string like

can_place_black[cell .. (cell + len[group] - 1)] = True

Here you can instead = Trueincrease the number by 1. And if we need to make a lot of additions on a segment in a certain array$$and, moreover, we do not use this array before various additions (they say about this that this task is “solved offline”), instead of a cycle:

# Много раз такой кодfor i in range(L, R + 1):
    array[i]++

You can do this:

# Много раз такой код
array[L]++
array[R + 1]--
# После всех прибавленийfor i in range(1, n):
    array[i] += array[i - 1]

Thus, the whole algorithm works for $$where $$ - the number of groups of black cells, $$- string length. And we go to the ACM ICPC semifinal or get the internum bronze. ACM Solution (Java) . Solution IOI (C ++) .

One line, many colors

When switching to multi-color nonograms, which are still not clear how to solve, we will learn the terrible truth - it turns out that every column has a magical effect on all the columns! This is clearer through an example:

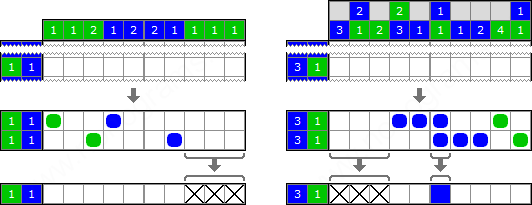
Source - Methods for solving Japanese crosswords

While the two-color nonograms normally did without it, they did not have to look back at orthogonal friends.
The picture shows that in the left-hand example the three rightmost cells are empty because the configuration will break if we paint these cells inthose colors in which to dye yourself non-white color.

But this joke is mathematically resolvable - each cell must be given a number, where $$th bit will mean whether you can give this cell $$th color Initially, all cells value$$. The solution dynamics will not change very much.

It will be possible to observe the following effect: in the same left example, according to the version of the rows, the rightmost cell can have either blue or white color.
According to the column version, this cell is either green or white.
According to the common sense version, this cell will have only white color. And then we continue to calculate the answer.

If the zero bit is considered white, the first is blue, the second is green, then the line calculated the state for the last cell $$and column $$. So, in fact, this cell has a state$$

source = [...]  # Начальные состояния
result = [0, 0, ..., 0]  # Итоговые состояния
len = [...]  # Длины групп клеток
clrs = [...]  # Цвета групп клетокdefCanInsertColor(color, cell, len):for i in range(cell, cell + len):
        if (source[i] & (1 << color)) == 0:  # В некоторой клетке цвет color поставить не можемreturnFalse;
    returnTruedefPlaceColor(color, cell, len):for i in range(cell, cell + len):                                           
        result[i] |= (1 << color)  # Добавляем цвет color операцией ORdefEpicWinExtended(group, cell):if cell >= last_cell: # Условие выигрыша                                    return group == group_size                                              
    win = False# Можем ли вставить группу в этой позиции                                   if group < group_size  # Группы еще есть                                    and CanInsertColor(clrs[group], cell, len[group])  # Вставка черной группыand SequenceCheck()  # Если следующая группа имеет тот же цвет, проверяем# что можем после этой группы поставить белую клеткуand EpicWin(group + 1, cell + len[group]):  # Можно заполнить далее 
        win = True                                                              
        PlaceColor(clrs[group], cell, len[group])                               
        PlaceColor(0, cell + len[group], 1)  # Белая клетка - только если нужно # Можем ли вставить белую клетку в этой позиции                             # Белая клетка - бит 0                                                      if CanInsertWhite(0, cell, 1)                                               
            and EpicWinExtended(group, cell + 1):                                                                                                      
        win = True                                                              
        PlaceColor(0, cell, 1)                                                  
    return win                      

Many rows many colors

Constantly doing the update of the states of all rows and columns, described in the last paragraph, until there is a single cell with more than one bit. In each iteration, after updating all rows and columns, update the states of all cells in them through mutual AND.

First results

Suppose that we wrote the code not like woodpeckers, that is, we don’t copy objects anywhere by mistake instead of passing by reference, we don’t invent bicycles anywhere, use bicycles __builtin_popcountand __builtin_ctz(for gcc features ) for bit operations , everything is neat and clean.

Let's look at the time of the program, which reads the puzzle from the file and solves it completely. It is worth assessing the merits of a machine on which all this stuff was written and tested:

RAM - 4GB
Процессор - AMD E1-2500, частота 1400MHz
Кэш L1 - 128KiB, 1GHz
Кэш L2 - 1MiB, 1GHz
Ядер - 2, потоков - 2
Представлен как «малопроизводительная SoC для компактных ноутбуков» в середине 2013 года
Стоимость процессора 28 долларов

It is clear that such a supercomputer was chosen, because optimizations on it have a greater effect than on a flying shaitan-machine.

So, after running our algorithm on the most difficult crossword (according to nonograms.ru), we get a not very good result - from 47 to 60 seconds (this includes reading from the file and the solution). It should be noted that the "complexity" on the site is well calculated - the same crossword in all versions of the program was also the hardest, the other most difficult crosswords in the opinion of the archive were kept in the top in time.

Color Crossword №9596, the greatest difficulty

For quick testing, the benchmark functionality was made. To obtain data for it, I sparsil 4683 color crosswords (out of 10906 ) and 1406 black and white (out of 8293 ) with nonograms.ru (this is one of the largest nonogram archives on the Internet) and saved them in a format understandable to the program. We can assume that these crosswords are a random sample, so the benchmark would show adequate average values. Also, the numbers of the pair of dozens of the most "difficult" crosswords (also the largest in size and number of colors) are written into the script for loading with pens.

Optimization

Here are possible techniques for optimization that were made (1) at the time of writing the entire algorithm, (2) for shrinking the operating time from half a minute to fractions of a second, (3) those optimizations that may be useful further.

At the time of writing the algorithm

• Special functions for bit operations, in our case __builtin_popcountfor counting ones in a binary number, and __builtin_ctzfor the number of zeros before the first and lowest unit. Such functions may not appear in some compilers. For Windows, suitable analogs are:

#ifdef _MSC_VER                                                                                                #  include<intrin.h>                                                                                          #  define __builtin_popcount __popcnt                                                                          #endif

• Array organization - the smaller size is at the beginning. For example, it is better to use the array [2] [3] [500] [1024] than [1024] [500] [3] [2].
• The most important thing is the general adequacy of the code and the avoidance of unnecessary worries for calculations.

What reduces the work time

• -O2 flag when compiling.
• In order not to throw the fully resolved row / column into the algorithm again, you can in the separate std :: vector / array start the flags for each row, mark them with a complete decision, and not let go further if there is nothing to decide.
• The specificity of a multi-repetition problem solving for dynamics implies that a special array that contains flags marking the already “computed” pieces of the problem should be reset every time with a new solution. In our case, this is a two-dimensional array / vector, where the first dimension is the number of groups, the second is the current cell (see the EpicWin pseudocode from above, where this array is not, but the idea is clear). Instead of zeroing, you can do so — let us have a “timer” variable, and the array consists of numbers that show the last “time” when this piece was recalculated last. When starting a new task, the "timer" is incremented by 1. Instead of checking the Boolean flag, check the equality of the array element and the "timer". This is effective especially in cases
• Replacement of simple operations of the same type (assignment cycles, etc.) with analogues in STL or more adequate things. Sometimes it works faster than a bike.
• std::vector<bool>in C ++, it compresses all Boolean values ​​to individual bits in numbers, which works on access a little slower than if it were a normal value at an address. If the program is very, very often refers to such values, then replacing the bool with an integer type can well affect performance.
• The remaining weaknesses can be searched through profilers and edit them. I myself use Valgrind, its performance analysis is convenient to look through kCachegrind. Profilers are built into many IDEs.

These edits were enough to get such data on the benchmark:

izaron@izaron:~/nonograms/build$ ./nonograms_solver -x ../../nonogram/source2/ -e
[2018-08-04 22:57:40.432] [Nonograms] [info] Starting a benchmark...
[2018-08-04 22:58:03.820] [Nonograms] [info] Average time: 0.00497556, Median time: 0.00302781, Max time: 0.215925
[2018-08-04 22:58:03.820] [Nonograms] [info] Top 10 heaviest nonograms:
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.215925 seconds, file 9596
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.164579 seconds, file 4462
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.105828 seconds, file 15831
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.08827 seconds, file 18353
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.0874717 seconds, file 10590
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.0831248 seconds, file 4649
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.0782811 seconds, file 11922
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.0734325 seconds, file 4655
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.071352 seconds, file 10828
[2018-08-04 22:58:03.820] [Nonograms] [info] 0.0708263 seconds, file 11824

izaron@izaron:~/nonograms/build$ ./nonograms_solver -x ../../nonogram/source/ -e -b
[2018-08-04 22:59:56.308] [Nonograms] [info] Starting a benchmark...
[2018-08-04 23:00:09.781] [Nonograms] [info] Average time: 0.0095679, Median time: 0.00239274, Max time: 0.607341
[2018-08-04 23:00:09.781] [Nonograms] [info] Top 10 heaviest nonograms:
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.607341 seconds, file 5126
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.458932 seconds, file 19510
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.452245 seconds, file 5114
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.19975 seconds, file 18627
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.163028 seconds, file 5876
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.161675 seconds, file 17403
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.153693 seconds, file 12771
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.146731 seconds, file 5178
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.142732 seconds, file 18244
[2018-08-04 23:00:09.781] [Nonograms] [info] 0.136131 seconds, file 19385

You can see that, on average, black and white crosswords are "more difficult" than color. This confirms the observations of game lovers, who also believe that the "color" are solved on average easier.

Thus, without radical revisions (such as rewriting the entire code to C or assembly inserts with fastcall and lowering the frame pointer) can be achieved by high performance, we note, on a very modest computer. The Pareto principle can be applied to optimizations - it turns out that small-scale optimization has a strong effect, because this piece of code is critical and is called very often.

Further optimization

The following methods can greatly improve program performance. Some of them do not work in all cases, but under certain conditions.

• Rewriting code in C-style and other year 1972. Replace ifstream with sishny analog, vectors with arrays, learn all the compiler options and fight for each processor clock.
• Parallelization. For example, in the code there is a piece where the rows are sequentially updated, then the columns:

    ...
    if (!UpdateGroupsState(solver, dead_rows, row_groups, row_masks)) {                                                                               
        returnfalse;                                                              
    }                                                                              
    if (!UpdateGroupsState(solver, dead_cols, col_groups, col_masks)) {           
        returnfalse;                                                              
    }                                                                             
    returntrue;

These functions are independent of each other and they do not have shared memory, except the variable solver (OneLineSolver type), so you can create two "solver" objects (only one is obvious here - solver) and run two threads in the same function. The effect is the same: in color crosswords, the “hardest” is solved twice as fast, in black and white the same one third faster, and the average time has increased, due to the relatively high costs of creating streams.

But in general, I would not advise doing it right in the current program and using it calmly - first, creating threads is a costly operation, you should not constantly create threads for microsecond tasks, and second, with some combination of program arguments, threads can access simultaneously - external memory, for example, when creating image solutions - this should be taken into account and secured.

If the task were serious and I would have a lot of data and multi-core machines, I would go even further - you can start several constant streams, each will have its own OneLineSolver object, and another thread-safe structure that drives the distribution of work and upon request it gives a reference to the next row / column for the solution. Flows after solving the next task turn to the structure again to solve something else. In principle, some nonogram problem can be solved without finishing the previous one, for example, when this structure is engaged in the mutual AND of all cells, and then some flows are free and do nothing. Another parallelization can be done on the GPU through CUDA - there are many options.

• Using classic data structures. Please note - when I showed pseudocode solutions for colored nonograms, the functions CanInsertColor and PlaceColor do not work at all for$$, unlike black and white nonograms. It looks like this in the program:

bool OneLineSolver::CanPlaceColor(constvector<int>& cells, int color,          
        int lbound, int rbound) {                                               
    // Went out of the border                                                   if (rbound >= cells.size()) {                                               
        returnfalse;                                                           
    }                                                                           
    // We can paint a block of cells with a certain color if and only if it is  // possible for all cells to have this color (that means, if every cell     // from the block has color-th bit set to 1)                                                                                                       int mask = 1 << color;                                                                                                                             
    for (int i = lbound; i <= rbound; ++i) {                                    
        if (!(cells[i] & mask)) {                                               
            returnfalse;                                                       
        }                                                                       
    }                                                                           
    returntrue;
}
void OneLineSolver::SetPlaceColor(int color, int lbound, int rbound) {                                                                                 
    // Every cell from the block now can have this color                        for (int i = lbound; i <= rbound; ++i) {                                    
        result_cells_[i] |= (1 << color);                                       
    }                                                                           
} 

That is, it works for the line, for $$ (Later there will be an explanation of the meaning of such a code).

Let's see how you can get the best difficulty. Take CanPlaceColor. This function checks that among all the numbers of the vector in the segment$$ bit number $$ set to 1. Equivalent to this you can take $$of all numbers of this segment and check bit number$$. Using the fact that the operation$$commutative , as well as sum, minimum / maximum, product, or operation$$for quick counting $$of the entire segment, you can use almost any data structure that works with commutative operations on the segment. It:

1. SQRT decomposition. Preliminary account$$, request $$. Article on Habré .
2. Segment tree. Preliminary account$$, request $$. Hundreds of articles on the Internet.
3. Sparse Table. Preliminary account$$, request $$. Article .

Unfortunately, especially strong witches like the algorithm of Farack-Colton and Bender (pre-count $$, request $$) can not be used, since you can understand the articles , they are created only for such operations$$, what $$, that is, the result of a commutative operation is one of the arguments (sorry, and so wanted ...)

Now take SetPlaceColor. Here it is necessary to perform an operation on the segment of the array. This can also be done with SQRT decomposition or a segment tree with a lazy update (it is also “pushing”). And for both functions at the same time, you can still use a Uber-structure Cartesian tree using an implicit key with an update and a query for logarithm.

You can also use the extension algorithm for black and white crossword puzzle - partial sums for all colors.

So, the question arises - why do not we use all this wealth as a component, but do it out of line? There are several answers to this:

1. Less computational complexity does not mean less work time. Algorithm for$$It may require different accounts, memory allocations, other resource shaking - this algorithm can have a rather high constant (not in the sense of the magic number in the neural goggles, but affect over the runtime). Obviously, if$$, then the conditional algorithm for $$ conditional 10 seconds will work, and conditional algorithm $$ for conditional 0.150 seconds, but everything can change when small enough $$especially when there are many such calculations. It is even more incomprehensible when the difficulties are very similar and one difficulty is difficult to kill another difficulty (complex jokes):$$ versus $$. In our task$$ (row length) is very small - on average about 15-30.
2. Requests may be small enough that the pre-calculations are useless and eat resources just like that.

That is, the explanation is simple - both of these points are performed and the insertion of these wonders of programming thought instead of a blunt algorithm either optimizes the program very poorly or only increases the running time due to the specifics of the calculations — a very small $$and not so many requests to load the processor. The fact about the requests proves that, according to the profiler, those functions take ~ 25% and ~ 11% of time, respectively, that is, quite a few for such a potentially weak program space. Even if we have a large estimate of the complexity of the algorithm because of this, it is worth understanding that in such types of tasks this is an estimate from above, and the actual time of working on a random crossword is always much lower.

But do not forget about data structures - they can be useful in other cases, so I included them in the list of optimizations. Go to the next list.

• Algorithm Edit. It may turn out that, on average, the algorithm on these inputs starts to work very well if you change something unobvious. In our case, this might be the following: it’s logical to assume that if we successfully updated the data in a row, then the cells updated in it most likely trigger the corresponding columns? So, it is better to update these columns the fastest, immediately after this line! That is, a queue of such subtasks is formed. I did not try just such an algorithm, maybe it’s really faster on our dataset.
• Sudden changes in the technical specifications (it turns out that crossword puzzles of 1337 colors or 1000x1000 in size are coming in) also require optimization. For a large number of colors, you can use fast std :: bitset , for size - the same data structures, and so on.

In general, these are such cool optimizations. Popping a poor algorithm depending on the conditions is fun and informative. You can learn about various cool things, like the built-in Cartesian tree using an implicit key in C ++ (this is rope , but bicycle writing is almost always faster), special built-in tree sorts and hidden hashtable , which works 3-6 times faster for insertion / deletion and 4-10 times write / read, than unordered_map. Not to mention the various non-standard mazafaki from the side, for example from boost.

ROFL Omitting Format Language

Inspired by the geniuses of bygone days and their mental products, in particular, completely new archiving algorithms and operating systems with boring wallpapers, I also came up with a fundamentally new image format based on Japanese crosswords and the Dunning-Kruger effect.

ROFL is a recursive acronym, just like "GNU's Not Unix". Actually, the meaning of the format is that the picture is encoded in the form of a Japanese crossword puzzle, and the editor, in order to read it, has to solve this crossword puzzle. Hence the word Omitting in the title - the format seems to hide the true state of affairs in the picture (which, by the way, can be useful in cryptography: you can transfer Japanese crosswords with passwords encrypted in it - all hackers will hang themselves).

It is better if the format would be similar to Matroska - at the beginning of the file 4 bytes [52] [4F] [46] [4C], then in three bytes the size of the picture and the number of colors, then the description of colors, then the colors, each 3 bytes, and then the description of all groups - length, number of cells and color.

The format is free, MIT license, financial deductions are voluntary - to me for coffee, as the author.

Sources

Sources of the program are on GitHub . The program has many possible arguments, the generation of a crossword puzzle from a picture, the generation of pictures from a crossword puzzle (by the way, almost all the pictures in the article are generated through this code). Additional libraries were Magick ++ and args .

In the picture repository for the crossword, I added several examples taken from the Internet (they are not part of the project). Sparsened thousands with nonograms.ru did not lay out anywhere and I will not, so that they would not be nagged, because they can be protected by rights and a gigger can expect interesting consequences.

I would like to express special thanks to the author of nonograms.ru, Chugunny K.A. KyberPrizrak , for creating the beautiful, the best and one of the largest nonogram website on the Internet, and for permission to use the materials for the article! I took all the examples in this article from nonograms.ru, here is a list of sources.

Sources .