Filtering false matches between images using a dynamic match graph

Many modern computer vision algorithms are based on the detection and comparison of specific points of visual images. A lot of articles were written on this topic on the Habré (for example, SURF , SIFT ). But most of the works do not pay due attention to such an important stage as filtering false matches between images. Most often, the RANSAC method is used for these purposes and they stop here. But this is not the only approach to solving this problem.
This article focuses on one of the alternative methods for filtering false matches.

Formulation of the problem

Suppose we have two sets of singular points obtained from two images P and Q with n _p and n _q points, respectively. Each singular point is a pair p = {p _d , p _c }. p _d - is a local feature of the point (for example, a SURF descriptor), and p _c = {x, y} is the coordinates of the feature point.
We have many correspondences M = {c _i = (i, i ') | c _i ∈ C, i ∈ P, i '∈ Q} constructed using some metric (for example, as points with the descriptors closest to the Euclidean metric). For each correspondence, we construct a non-negative estimation function S _{c i} = f ₁ (i _d, i ' _d ).

For the two correspondences c _i = (i, i ') and c _j = (j, j'), suppose that the distance between points i and j in the first image and points i 'and j' in the second image l _ij and l _{i ' j ',} respectively. Obviously, if these two matches are true, then we can align the image Q with P with a scale factor l _ij frasl; l _{i'j '} , and we say that this pair of matches votes for the scale l _ij frasl; l _{i'j '}. Now suppose that there is a visual image with n correct matches corresponding to it, then for each pair of these matches the scale factor should be approximately the same. Such a scale will be called the scale factor of geometric consistency and denoted by s. The scale coefficient of geometric consistency of the pair of correspondences c _i = (i, i ') and c _j = (j, j') is expressed as:
S _{c i c j} (s) = f ₂ (| l _ij - s * l _{i'j '} |), where f ₂ (x) is a non-negative monotonically decreasing function.

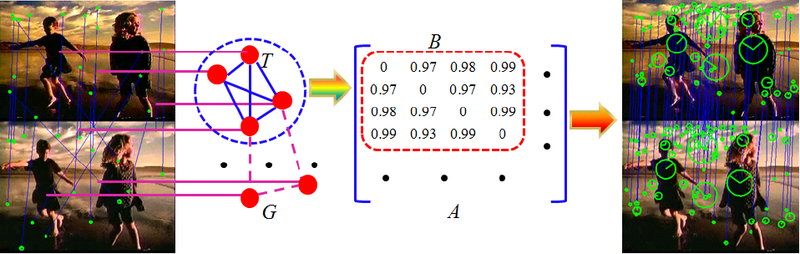
Let the set M contain m correspondences M = {c ₁ , ..., c _m}. We construct a graph G with m vertices, each vertex of which represents a correspondence from M. The weight of an edge between vertices i and j is defined as follows:
w _ij (s) = S _{c i} * S _{c j} * S _{c i c j} (s).
The graph constructed in this way will be called the Dynamic Correspondence Graph (hereinafter referred to as DGS).

We denote the weighted adjacency matrix for DGS by A (s) and construct it as follows:

A (s) ∈ R ^{m * m} - symmetric and non-negative.

The correct visual image containing n singular points corresponds to a complete subgraph T ∈ G with n vertices, which, as can be easily seen, is a weighted duplicate of the maximum clique. This subgraph has a high average intra-cluster evaluation:

If we imagine a T-vector y indicator such that 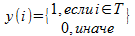, the average inter-cluster score may be written in quadratic form:
where , .

As is known, the Motzkin-Strauss theorem establishes a connection between the maximum clique and the local maximum of such a quadratic form:,
where is the standard simplex in R ^m. Simply put, the theorem says that a subset T of vertices of a graph G is a maximal clique if and only if its characteristic vector x ^T is the local maximum of the quadratic function f (x) in the standard simplex, where x _i ^T = 1⁄ | T | if i ∈ T, x _i ^T = 0 otherwise.

Although the original Motzkin-Strauss theorem applies only to unweighted graphs, Pavan and Pelillo generalized it to weighted graphs and established a connection between dense subgraphs and local maxima of the equations.

The accepted norm l ₁ has several advantages. Firstly, it has a simple probabilistic meaning: x _irepresents the probability that a complete subgraph contains vertex i. Secondly, the solution x is sparse, and only some components in the same subgraph are of great importance, the remaining components are quite small, which allows us to isolate the cluster by discarding those vertices that are noise, which are noise.

Thus, the task of filtering correspondences is reduced to the problem of finding clusters of correspondences representing individual visual images. In turn, in order to find such clusters, it is necessary to solve the optimization problem described above.

Algorithm description

For scale s ₀ , the optimization problem can have many local maxima. Each large local maximum most often corresponds to the correct visual image, and the small local maximum most often occurs as a result of noise.

When initializing x (1), the corresponding local solution x can be efficiently obtained by using the equation of the first order self-assembly having the form:


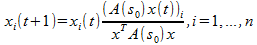
It can be seen that the simplex Δ is invariant with respect to this dynamic, which means that any path starting at Δ, will remain in the Δ . In addition, it was proved that when A (s ₀ ) is symmetric and with non-negative elements, the objective functionstrictly increases along any non-constant trajectory of the self-assembly equation, and these asymptotically stable points are in strict one-to-one correspondence with local solutions of a quadratic function.

Roughly speaking, in order to find all large local maxima of x, they take many initial initializations and thus guarantee that all large local maxima at a given simplex will be taken into account. As mentioned above, for our task, each local maximum corresponds to a visual image, then it must have two properties:

1. Locality property. The singular points of one visual image lie in some small neighborhood, so we need to initialize x (1) only in the vicinity of each vertex of the GVD.
2. Non-intersection property. Different visual images, as a rule, do not contain common vertices in G, which means that if two local maxima x and y correspond to two different visual images, then (x, y) ~ 0.

Since we initialized x (1) for each vertex of the DGS and initialized the vertices of the same visual image converge to approximately one local maximum, we must merge the local maxima corresponding to the same visual images. Due to this data redundancy, additional noise immunity is achieved. All small local maxima corresponding to noise are also discarded.

In the end, it is necessary to restore the visual image for each local maximum x. Because x _i represents the probability of the vertex i entering the visual image of x; we can only select those vertices whose entry into the visual image is most likely.

Algorithm parameters

As can be seen from the above description, the algorithm has a large number of configurable parameters such as:

• S _{c i} = f ₁ (i _d , i ' _d ) - conformity assessment function
• S _{c i c j} (s) = f ₂ (| l _ij - s * l _{i'j '} |) - function for evaluating the geometric consistency of correspondences
• Ε - threshold value for estimating the weight of the rib, for belonging to the neighborhood of initialization
• Φ is the radius of the neighborhood for which initialization x (1) is taken
• Ψ is the threshold value for assessing the smallness of the local maximum
• Ω - threshold value for merging neighborhoods
• Θ - threshold value of the probability of the vertex entering the visual image

The experiments

Typical results of the algorithm are presented below.

Conclusion

The practical application of the described algorithm is difficult due to the high sensitivity to the algorithm parameters, which are selected empirically for each set of input data. Also, for the effective application of this method, a preliminary analysis of the input set of correspondences is required for the allocation of dominant scale factors.
Due to the fact that the fight against noise occurs due to data redundancy, the algorithm requires a large amount of additional memory and processing time.
Therefore, this algorithm is interesting from the point of view of the approaches used in it to analysis of correspondence, and not as an alternative, for example, to the RANSAC method mentioned at the beginning of the article.

Literature

• Common Visual Pattern Discovery via Spatially Coherent Correspondences Hairong Liu, Shuicheng Yan, Departament of Electrical and Computer Enginering, National University of Singapore, Singapore
• T. Motzkin and E. Straus. Maxima for graphs and a new proof of a theorem of Turan. Canad. J. Math, 1965.
• 10. M. Pelillo, K. Siddiqi, and S. Zucker. Matching hierarchical structures using association graphs. TPAMI, 1999.

UPD Link to the method sources: dl.dropbox.com/u/15642384/src.7z