The game "Life". Again. This time in 3D
Over the past week, Habr was replenished with several articles about the game "Life". Well, then I will share my best practices on this topic.
Last summer I happened to attend the summer school on parallel programming conducted by NSU. Within the school, each student had to prepare a project on one of the topics voiced at the lectures. I was interested in cellular automata. My first association with the phrase “cellular automaton” is precisely “Life”.
I realized that no one would be interested in watching the black cells living on the screen. And it's too simple for such a project. It was necessary to come up with something fundamentally new. I decided to expand the range of my thoughts and go beyond two-dimensional space. Literally. I thought, why not make this game three-dimensional? After all, it is much more interesting!
I think that here everyone (well, or almost everyone) imagines a cellular automaton. Therefore, we will not delve into theory, but immediately move on to practice. The only thing that distinguishes this cellular automaton from the most primitive one is that it was necessary to parallelize the calculations. In the future, however, something else will be added, but for now we will not talk about it. The cellular automaton (hereinafter KA) for our purposes must be synchronous. Fortunately, even with a parallel implementation of the algorithm, this does not create any inconvenience. When working with OpenMP, it's enough to just put a loop that calculates the value of the spacecraft in the #pragma omp for {} block.
It would not be bad if all this could be seen firsthand. And I was lucky because literally a month before that I had little, little mastery of working with OpenGL using the freeglut library. I also wanted the game space to be able to rotate, zoom in and out. Management is carried out using the mouse and keyboard. The mouse rotates, the keyboard moves. The keyboard also controls the Life itself. Since the perception of three-dimensional space requires more time than for two-dimensional space, it was decided to proceed to the next step by pressing a key.
The first tests of the visualizer passed with a bang. But when trying to slip him an array of 100 * 100 * 100 (or more, I don’t remember exactly) the cells, each frame was drawn up to 8 seconds. This is not the case. Then I remembered the pyramid of visibility. Unfortunately, drawing on this very pyramid took almost the same time, since most of the time the space was completely visible. When approaching the center of this space and further movement beyond it, the rendering time decreased significantly.
There was still time, and the project was already ready for delivery. I realized that something was missing. But what exactly - the question is more complicated. After some time of thought, I decided that my spacecraft was not at all like real life. There are not enough external factors affecting cell reproduction. The temperature was chosen as such a factor.
Briefly, that is, there is a certain temperature, we call it optimal, at which the survival and birth rate are maximum. With a decrease and increase in temperature, survival becomes more difficult. But just setting the temperature would not be interesting. And again, resort to the spacecraft. In the initial state, the temperature is concentrated in the center of space. Over time, “warm air” is evenly distributed throughout the space. This is achieved by diffusion. Yes, not simple, but integer. In this case, this consists in the fact that some of the temperature in the cell remains, and the neighboring cells exchange the rest. Such a cellular automaton can no longer be synchronous, since you were strange if all the cells changed at the same time ... And so that it could be programmed for several processes, it’s necessary to resort to tricks - to switch from an asynchronous spacecraft to a block-synchronous one. The point is that each process is allocated a block. Inside this block, the spacecraft is asynchronous. But the blocks are synchronized with each other. In the picture, cells of the same color are calculated at one time.

Of course, this implementation is not ideal. The code is not optimized in any way. First of all, you can improve the visualizer. In addition to clipping along the visibility pyramid, add clipping along the Z-buffer so that those cells that are hidden by the foreground cells are not drawn.
In general, a project can be inflated to a cosmic scale. For example, I want to add additional layers. If we talk only about external influences, then it can be, for example, a relief. At high altitudes, the cells will be less likely. Moreover, it will be colder there. You can add a layer of vegetation that will serve as food. And you can clone the layer with the cells themselves and create several types of organisms that will eat each other. You can add mutations and much, much more. It would be a desire.
Now, finally, we can move on to the most interesting.
At first, the program was tested without a temperature layer, since by then it simply was not there. Unfortunately, the program does not have a normal interface, and I had to write a test generator. He is not of particular interest. His only task is to make a cube of cells in the center of the playing space. Below are cubes 3x3x3, 4x4x4 and 5x4x5. Here are just a few steps to get a general picture of what is happening.
3x3x3, step 1:
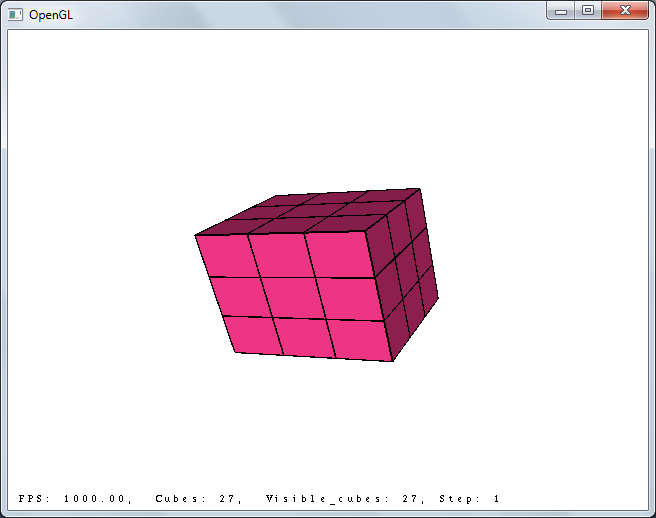
3x3x3, step 4:
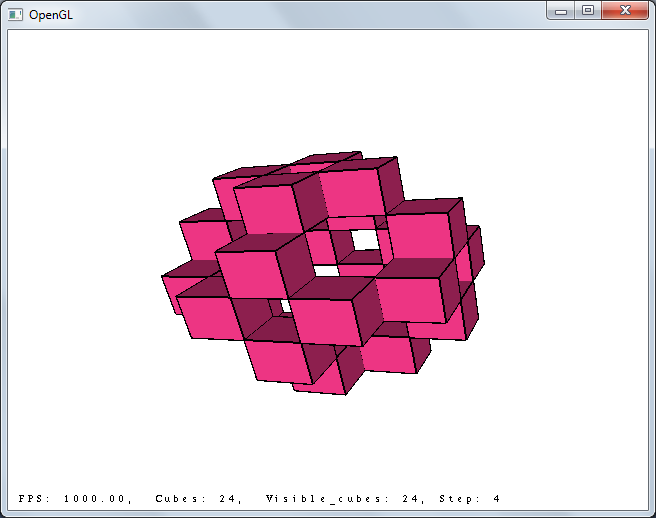
3x3x3, steps 5 and 6:
It turns out pretty funny flasher.
4x4x4, step 1:
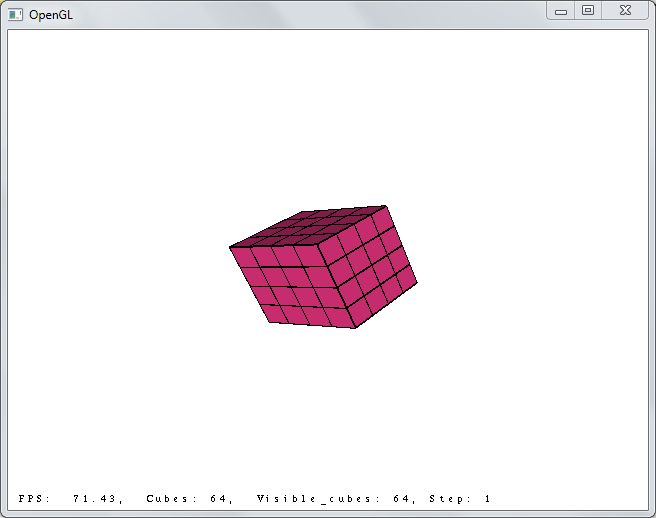
4x4x4, step 10:
4x4x4, step 100:
Further, practically nothing changes.
5x5x5, step 1:

5x5x5, step 4:
5x5x5, step 7:

5x5x5, step 8:
In the next step, no living cells remain.
Now add the temperature to the 4x4x4 cube. The temperature layer is presented as a central cut. Red is the optimum temperature, yellow is slightly below normal, and pink is low. The game space has dimensions 50x50x50, in the center there is a 40x40x40 cube with optimal temperature. Here's what happened.
Step 1:

Step 10:
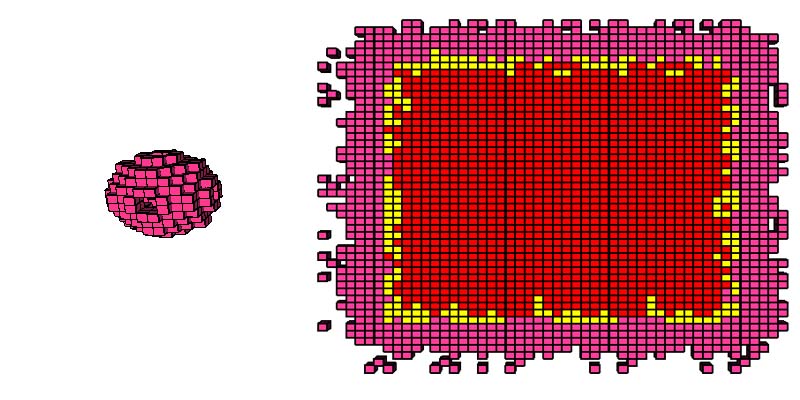
Step 50:

Step 150:

Step 200:

Everything is very clear: the air cools down, life stops.
Unfortunately, I can’t share the program itself, since the input data is hardcoded in the generator. But I can share the source, but I warn you right away: the code is just awful.
Foreword
Last summer I happened to attend the summer school on parallel programming conducted by NSU. Within the school, each student had to prepare a project on one of the topics voiced at the lectures. I was interested in cellular automata. My first association with the phrase “cellular automaton” is precisely “Life”.
I realized that no one would be interested in watching the black cells living on the screen. And it's too simple for such a project. It was necessary to come up with something fundamentally new. I decided to expand the range of my thoughts and go beyond two-dimensional space. Literally. I thought, why not make this game three-dimensional? After all, it is much more interesting!
Stage 1. Cellular Automaton
I think that here everyone (well, or almost everyone) imagines a cellular automaton. Therefore, we will not delve into theory, but immediately move on to practice. The only thing that distinguishes this cellular automaton from the most primitive one is that it was necessary to parallelize the calculations. In the future, however, something else will be added, but for now we will not talk about it. The cellular automaton (hereinafter KA) for our purposes must be synchronous. Fortunately, even with a parallel implementation of the algorithm, this does not create any inconvenience. When working with OpenMP, it's enough to just put a loop that calculates the value of the spacecraft in the #pragma omp for {} block.
Something like this
#pragma omp parallel shared(Temp, Space, Size) private(Num_of_nbr, x, y, z)
{
#pragma omp forfor (x = 0; x < Size; x++)
for (y = 0; y < Size; y++)
for (z = 0; z < Size; z++)
{
// Neighbors(x, y, z) вычисляет кол-во соседей//у клетки с координатами x, y и z
Num_of_nbr = Neighbors(x, y, z);
if (Space[x][y][z] == 1)
if (Num_of_nbr <= Smid + Sdiff * Koeff[Int_Temp[x][y][z]] \
&& Num_of_nbr >= Smid - Sdiff * Koeff[Int_Temp[x][y][z]])
Temp[x][y][z] = 1;
else Temp[x][y][z] = 0;
elseif (Num_of_nbr <= Bmid + Bdiff * Koeff[Int_Temp[x][y][z]] \
&& Num_of_nbr >= Bmid - Bdiff * Koeff[Int_Temp[x][y][z]])
Temp[x][y][z] = 1;
else Temp[x][y][z] = 0;
}
#pragma omp forfor (x = 0; x < Size; x++)
for (y = 0; y < Size; y++)
for (z = 0; z < Size; z++)
Space[x][y][z] = Temp[x][y][z];
}
Stage 2. Visualizer
It would not be bad if all this could be seen firsthand. And I was lucky because literally a month before that I had little, little mastery of working with OpenGL using the freeglut library. I also wanted the game space to be able to rotate, zoom in and out. Management is carried out using the mouse and keyboard. The mouse rotates, the keyboard moves. The keyboard also controls the Life itself. Since the perception of three-dimensional space requires more time than for two-dimensional space, it was decided to proceed to the next step by pressing a key.
The first tests of the visualizer passed with a bang. But when trying to slip him an array of 100 * 100 * 100 (or more, I don’t remember exactly) the cells, each frame was drawn up to 8 seconds. This is not the case. Then I remembered the pyramid of visibility. Unfortunately, drawing on this very pyramid took almost the same time, since most of the time the space was completely visible. When approaching the center of this space and further movement beyond it, the rendering time decreased significantly.
Stage 3. External influences
There was still time, and the project was already ready for delivery. I realized that something was missing. But what exactly - the question is more complicated. After some time of thought, I decided that my spacecraft was not at all like real life. There are not enough external factors affecting cell reproduction. The temperature was chosen as such a factor.
Briefly, that is, there is a certain temperature, we call it optimal, at which the survival and birth rate are maximum. With a decrease and increase in temperature, survival becomes more difficult. But just setting the temperature would not be interesting. And again, resort to the spacecraft. In the initial state, the temperature is concentrated in the center of space. Over time, “warm air” is evenly distributed throughout the space. This is achieved by diffusion. Yes, not simple, but integer. In this case, this consists in the fact that some of the temperature in the cell remains, and the neighboring cells exchange the rest. Such a cellular automaton can no longer be synchronous, since you were strange if all the cells changed at the same time ... And so that it could be programmed for several processes, it’s necessary to resort to tricks - to switch from an asynchronous spacecraft to a block-synchronous one. The point is that each process is allocated a block. Inside this block, the spacecraft is asynchronous. But the blocks are synchronized with each other. In the picture, cells of the same color are calculated at one time.

Integer diffusion
#pragma omp parallel shared(Size, BlockSize, Int_Temp, PosCell, PosNbr, DiffKoeff)\
private(CellNum, NbrNum, x, y, z, Cell1, Cell2, Rem1, Rem2, Mov1, Mov2)
{
CellNum = rand() % 27;
#pragma omp forfor (x = 1; x < Size; x += BlockSize)
for (y = 1; y < Size; y += BlockSize)
for (z = 1; z < Size; z += BlockSize)
{
NbrNum = rand() % 6;
Cell1 = Int_Temp[(x + PosCell[CellNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + Size) % Size];
Cell2 = Int_Temp[(x +PosCell[CellNum][0] + PosNbr[NbrNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + PosNbr[NbrNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + PosNbr[NbrNum][2] + Size) % Size];
//DiffKoeff определяет, какой процент температуры //останется в клетке, а какой перейдет в соседнюю.
Rem1 = Cell1 * (float)(1.0 - DiffKoeff);
Rem2 = Cell2 * (float)(1.0 - DiffKoeff);
Mov1 = Cell1 * DiffKoeff;
Mov2 = Cell2 * DiffKoeff;
if ((float)Cell1 * DiffKoeff - (float)Mov1 > (float)(rand() % 10) / 10.0)
Rem1++;
elseif ((float)Cell1 * DiffKoeff - (float)Mov1)
Mov1++;
if ((float)Cell2 * DiffKoeff - (float)Mov2 > (float)(rand() % 10) / 10.0)
Rem2++;
elseif ((float)Cell2 * DiffKoeff - (float)Mov2)
Mov2++;
Int_Temp[(x + PosCell[CellNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + Size) % Size] = Mov2 + Rem1;
Int_Temp[(x +PosCell[CellNum][0] + PosNbr[NbrNum][0] + Size) % Size] \
[(y + PosCell[CellNum][1] + PosNbr[NbrNum][1] + Size) % Size] \
[(z + PosCell[CellNum][2] + PosNbr[NbrNum][2] + Size) % Size] \
= Mov1 + Rem2;
}
}
Further perspectives
Of course, this implementation is not ideal. The code is not optimized in any way. First of all, you can improve the visualizer. In addition to clipping along the visibility pyramid, add clipping along the Z-buffer so that those cells that are hidden by the foreground cells are not drawn.
In general, a project can be inflated to a cosmic scale. For example, I want to add additional layers. If we talk only about external influences, then it can be, for example, a relief. At high altitudes, the cells will be less likely. Moreover, it will be colder there. You can add a layer of vegetation that will serve as food. And you can clone the layer with the cells themselves and create several types of organisms that will eat each other. You can add mutations and much, much more. It would be a desire.
results
Now, finally, we can move on to the most interesting.
At first, the program was tested without a temperature layer, since by then it simply was not there. Unfortunately, the program does not have a normal interface, and I had to write a test generator. He is not of particular interest. His only task is to make a cube of cells in the center of the playing space. Below are cubes 3x3x3, 4x4x4 and 5x4x5. Here are just a few steps to get a general picture of what is happening.
3x3x3, step 1:

3x3x3, step 4:

3x3x3, steps 5 and 6:

It turns out pretty funny flasher.
4x4x4, step 1:

4x4x4, step 10:

4x4x4, step 100:

Further, practically nothing changes.
5x5x5, step 1:

5x5x5, step 4:

5x5x5, step 7:

5x5x5, step 8:

In the next step, no living cells remain.
Now add the temperature to the 4x4x4 cube. The temperature layer is presented as a central cut. Red is the optimum temperature, yellow is slightly below normal, and pink is low. The game space has dimensions 50x50x50, in the center there is a 40x40x40 cube with optimal temperature. Here's what happened.
Step 1:

Step 10:

Step 50:

Step 150:

Step 200:

Everything is very clear: the air cools down, life stops.
Unfortunately, I can’t share the program itself, since the input data is hardcoded in the generator. But I can share the source, but I warn you right away: the code is just awful.
Source code
