A bit about chaos and how to create it
Saying “chaos”, we usually mean a complete lack of order, absolute disorder and randomness. From a mathematical point of view, chaos and order are not mutually exclusive concepts. Chaos theory (there is something fascinating in the names of mathematical theories) is a fairly young mathematical field, the creation of which is equated by the significance of the discoveries of the twentieth century with the creation of quantum mechanics. Chaos happens in nonlinear dynamical systems. In other words, any process that occurs over time can be chaotic (for example, tree height, body temperature, or a population of Madagascar cockroaches).
To understand what chaos is, we first turn to systems that are not endowed with such a feature. Deterministic systems do not allow any accidents: the value at the output is completely determined by the values at the input. Thus, a change in the initial conditions causes a proportional change in the result. Thus, Newtonian mechanics implies determinism, and by changing, for example, the strength of a kick over the ball, a corresponding change in the duration of the flight of this ball can be expected. So, according to the principle of determinism, the position of the ball at the current moment is completely determined by the position of the ball at the previous moment and the future position depends on the current one and it’s all very easy to calculate. So, and astronomers of the past time completely trusted this principle and believed that the universe is a strictly determined system and the position of celestial bodies in the future (and in the past) can be calculated by knowing their current position and speed, i.e. knowing the initial conditions. It was assumed that the more accurately the initial conditions are known, the more accurate the forecast result will be, however, the famous mathematician Henri Poincaré, who (in his spare time, probably) was engaged in describing the orbits of celestial bodies, found that in systems of 3 or more bodies, with a slight changes in the initial conditions (position and speed), the trajectories of the body are very quickly removed from each other. Two close sets of initial conditions gave different results. however, the famous mathematician Henri Poincaré, who (in his spare time, probably) was engaged in the description of the orbits of celestial bodies, found that in systems of 3 or more bodies, with a slight change in the initial conditions (position and speed), the trajectories of the body very quickly delete each other from friend. Two close sets of initial conditions gave different results. however, the famous mathematician Henri Poincaré, who (in his spare time, probably) was engaged in the description of the orbits of celestial bodies, found that in systems of 3 or more bodies, with a slight change in the initial conditions (position and speed), the trajectories of the body very quickly delete each other from friend. Two close sets of initial conditions gave different results.
Meteorologist Edward Lorenz made a great contribution to chaos theory. In the sixties of the last century, this American worked on a computer program simulating the movement of air masses in the Earth’s atmosphere. We all know that a computer (contrary to popular rumors) is a strictly deterministic system, and this creates the well-known principle of “garbage in garbage out”. Lorenz drove his program in the tail and mane, getting all sorts of different results. Some of his colleagues even made the assumption that this model is an accurate predictor of the weather, asked whether to take an umbrella tomorrow. Of course, these conclusions were hasty, one feature of the weather model soon became clear. Once to speed up the calculations, Lorenz did not start the program first, but entered data from the previous “run” into it, which were printed on paper. However, the results of such a launch quickly began to deviate from those already received, forming a completely different picture. A bit unexpected, right? It turned out that Lorentz did not introduce the exact results of past calculations, but rounded before printing, this error was simply ignored. The Lorentz model turned out to be hypersensitive to the initial conditions. The slightest difference in the input data led to a strong discrepancy between the results over time. This dependence on the initial conditions was called chaos. Lorentz voiced the famous trait of chaos called the “butterfly effect”, which suggests that depending on whether the butterfly flaps its wings in the forests of Brazil, it depends on whether a hurricane occurs in Texas or not. The same principle was the basis of the film of the same name with Ashton Kutcher (unscientific movie, not necessary to watch).
Recalculation Deviation
All this dependence on initial conditions suggests that we cannot make long-term forecasts in unstable dynamic systems. Any error in the initial conditions will not allow us to predict the result for any long period of time. If, for example, we take the Lorenz model, we will need to enter the temperature and pressure at each point on the Earth’s atmosphere as input to determine the wind speed, only then we can expect a reliable forecast for a long time. Moreover, the input data must be absolutely accurate, that is, with an infinite number of decimal places. And as you know, absolutely all measuring devices on Earth have a non-zero error. No matter how accurately a quantity is measured, it is always possible (theoretically) to measure more accurately. Yes and no such cars, which would allow you to enter an infinite number of decimal places. Maybe with the advent of quantum computers, something will change, I don’t know.
So it turns out that there is no escape from chaos and that we must put up with it. But not everything is so bad, in my opinion. If all processes in the universe were completely determinate, without a single hint of chance, life would be much more boring. Some scientists are even inclined to the idea that chaos gives the universe an “arrow of time”, a directed and irreversible movement from the past to the future.
However, “chaos” and “randomness” are not completely equivalent concepts. A certain interpretation of processes that seem random, puts them in order. For example, the time between heartbeats of a person is variable, even if a person is not subject to physical activity. If we observe the heartbeat for some time and write the intervals between the beats in the table, and also create a second column, copying the values from the first, but with a shift by one value (i.e., the second dimension will correspond to the first dimension (t) in the first column (t + 1) in the second, second - third, etc.;), it will be possible to build a map where vertically we will have values without a shift (t), and horizontally - values with a shift (t + 1). Points on this map will not be scattered randomly, but will be attracted to a certain area, forming an attractor.
A common example of a chaotic system is a double pendulum, i.e. a pendulum to the end of which a second pendulum is attached. You may have seen similar pendulums in gift shops. So, if you take two identical pendulums, place them side by side and reject them by approximately equal amounts, then after a few oscillations the pendulums are completely out of sync. The more precisely we observe the initial conditions, the longer the pendulums will swing to the beat, but there is no escape from the divergence.

Such patterns are drawn by a light bulb on a double pendulum by artist George Ioannidis
For a long time, chaos theory was considered a kind of mathematical abstraction, which has no confirmation in real conditions. This problem worried one Japanese named Leon Chua, who was aiming to show that chaos could be created. For this purpose, he assembled an electrical circuit.
The Chua circuit was the first electric circuit capable of generating chaotic signals. His creation was brilliant in its simplicity, the circuit consisted of four linear elements: two capacitors, one inductance and a resistor, and also included one nonlinear locally active element, on the piecewise-linear volt-ampere characteristic of which there was a region with negative resistance. This element is now often called the Chua diode. The circuit is a generator, and the Chua diode is a necessary part to achieve chaotic oscillations. This item is not available as a separate component, but it is easy to assemble using two operational amplifiers. Other ways to implement this non-linearity include a counter-parallel connected pair of inverters or a tunnel diode (it seems that it’s still available,
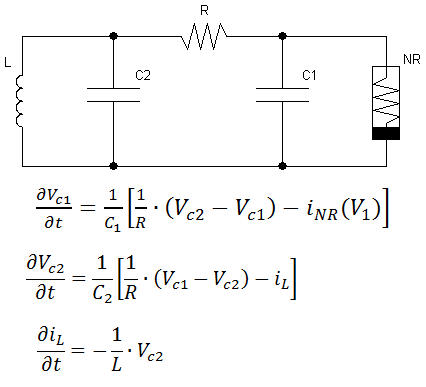
A generalized diagram of the Chua generator and the equations describing it. The
mathematics behind all this is quite complicated, but if you do not go into the wilds, this circuit is described by three differential equations showing the time variation of the voltage across two capacitors and the current through the inductance. The numerical solution of these equations shows that for certain relations between the components of the circuit, a change in the values of the variables in time becomes chaotic.
It’s not difficult to assemble a Chua generator. This chain can demonstrate chaos phenomena such as bifurcations and a chaotic attractor. However, to observe all these miracles, an oscilloscope will be needed, and even with two inputs. In the classic version, the circuit consists of two capacitors, one inductance, seven resistors, a microcircuit with a pair of operational amplifiers and two 9V batteries (you can use a power supply, but the power must be bipolar). To achieve chaotic behavior, certain ratios must be observed between element values. So, the capacitance of the capacitor C2 should be about 10 capacitances C1, the ratio C2 / C1 is called α. The coefficient β shows the relationship between R, C2 and L, namely β = R ^ 2 C2 / L and should be approximately 15.
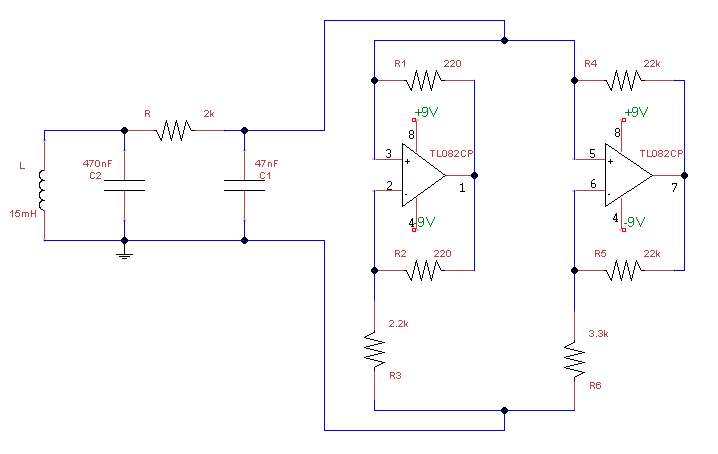
Schematic diagram of a generator with negative resistance on operational amplifiers
So, let's start the assembly. You can also assemble it on a breadboard, but to make the signals clearer, it is better to solder the components on a printed circuit board. In my assembly, I used 47nF and 470nF capacitors, an inductance of 15mH and a potentiometer of 1kΩ (for lack of a nominal value of 2kΩ, connected it in series with a 1kΩ resistor). In series with the inductance, you can (but not necessarily) include a small resistor (up to 10 Ohm) to add “beauty” to the signals. Chua diode is implemented in a standard way, using two opamps. I used the TL082CP chip, according to the specification, it is a broadband operational amplifier, I advise you to use this type, with simpler analogs, the circuit did not start up. To create a characteristic with the necessary slopes, we need the following resistors: R1 = R2 = 220 Ohm, R3 = 2.2k Ohm, R4 = R5 = 22kOhm, R6 = 3.3kOhm. The opamp can be powered with two 9V batteries, for the correct operation of the op-amp, we need bipolar power. My assembly is clumsy, I agree - power wiring and twisted resistors, other minor flaws, but this was enough to monitor chaotic signals.

We’ll save the rest of the board for the following projects
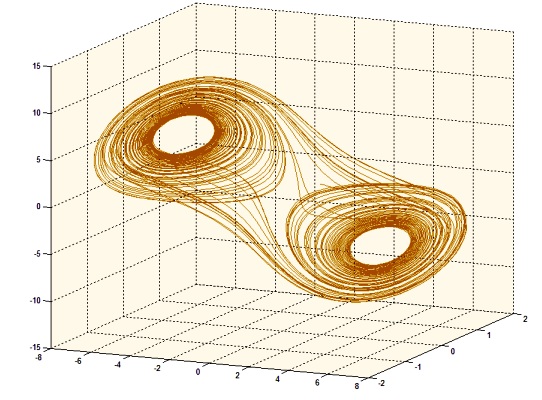
After carefully assembling this simple circuit, you can try to see what kind of signals it generates. We will take signals from capacitors C1 and C2. On my circuit, I made two BNC connectors for the convenience of connecting the circuit to an oscilloscope. We connect the cables to the oscilloscope and select the XY mode, when on one axis we will have voltage on the first capacitor, and on the other - voltage on the second. What to output on X and what on Y does not matter. Unscrew the handle of the potentiometer to the maximum value and feed the circuit. A dot should appear on the oscilloscope screen. Slowly decrease the resistance value (it is better to use potentiometers with a large stroke and with a large handle in order to ensure a smooth change in resistance), at some point the point should turn into an orbit. A subsequent decrease in resistance leads to a bifurcation of this orbit, we begin to observe bifurcations. Doubling the period of the orbit will continue to occur with a decrease in resistance, the distance between subsequent bifurcations will constantly and steadily decrease. Those. the difference in resistance between the quadruple and eightfold orbit will be less than between the quadruple and double. The rate at which the interval between bifurcations decreases is determined by the Feigenbaum constant. The period before which you will be able to observe bifurcations depends on the clarity of the signals (i.e., the quality of the connections) and the sensitivity of the potentiometer (hand shake is also not good). At some point, a stable orbit gives way to a two-loop attractor, which marks the onset of chaos. This attractor has three equilibrium points: one at the origin, and two in the “holes” of the loops. A typical trajectory of an attractor begins to rotate around one of the “holes”, moving away from the equilibrium point with each turn, then the trajectory either returns closer to the center and again moves away, or goes to another equilibrium point, where the process repeats. The number of rotations in each case is random.
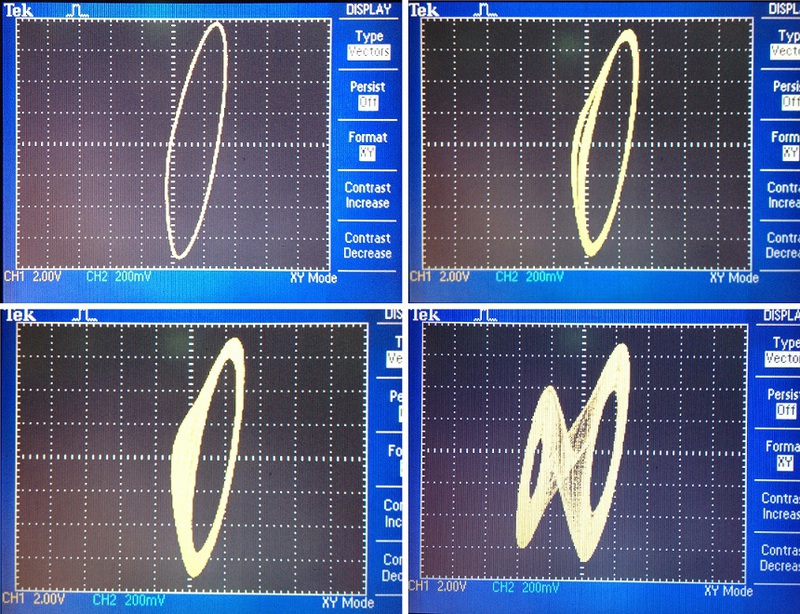
The formation of chaos through bifurcations
This attractor will exist in a certain range of resistance, and then give way to a stable orbit, showing harmonic oscillations. With sufficiently small resistance values, the circuit turns into a simple oscillatory circuit generating a sinusoidal signal with a frequency determined by the values of the capacitors and inductance. For greater "flexibility" of the circuit, potentiometers can replace the resistors in the negative resistance circuit.
If we look at the spectrum of signals, we will see that in the chaotic mode the lasing band is wide enough and does not have pronounced peaks, and it also starts with a constant component.
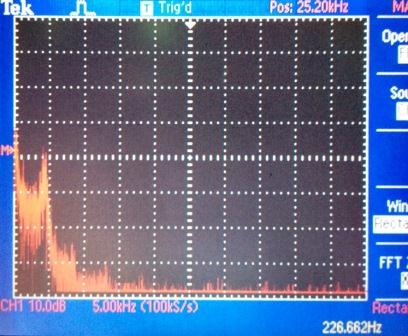
Chaotic signal spectrum
The scheme is extremely simple, but its behavior has been studied by many scientists working with the theory of chaos. With its help, bifurcations were studied and a whole gallery of various attractors was created. However, in addition to purely scientific interest, this scheme has practical applications.
Since this is a generator, it means that it can be used for radio communications, and since this generator is unusual, radio communications can be made secure. There are several types of modulation of a chaotic signal, from simple masking of the information signal to high-level digital modulation. The high sensitivity of the chaotic generator allows its use as a detector of weak signals. It was also reported on the creation of a random number generator based on this scheme. In addition, as you noticed, the spectrum of this generator lies in the sound range, so conceptual musicians did not fail to take advantage of this scheme.
I don’t know how many people want to assemble this chaotic generator, because its practical use is not enough, but it seems to me that the opportunity to play with it and observe interesting patterns on the oscilloscope is worth these penny details and half an hour of time. Even if you buy all the components individually at a store, 200 rubles is the maximum that you can spend, but I’m sure that many people have all the details in the sinkers!
This scheme may be of interest to students of mathematical and electrical engineering departments. I think that demonstrating the work of the Chua generator will be able to interest teachers whose scientific interests include chaos theory. Thank you all for your attention!
